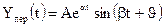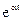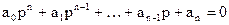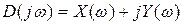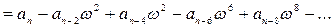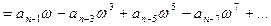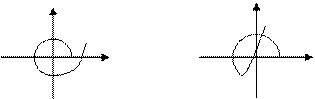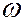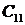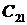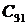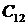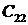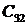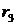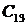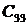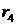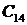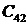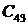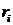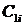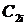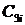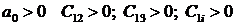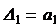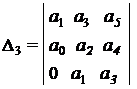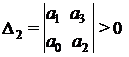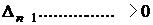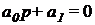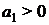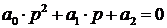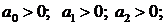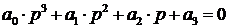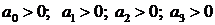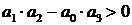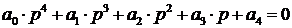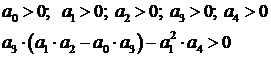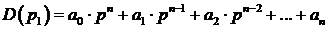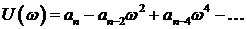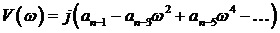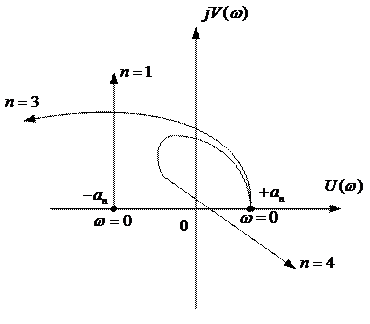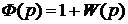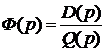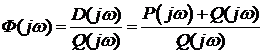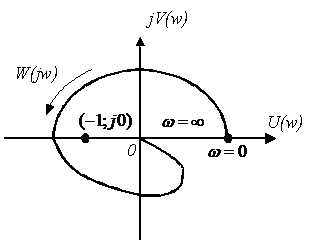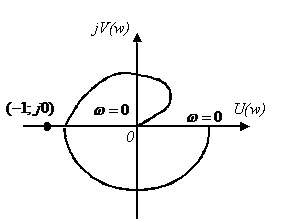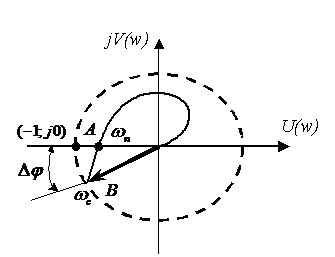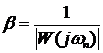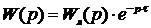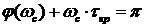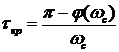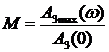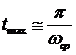1) 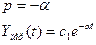
Устойчивая система.
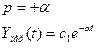
Неустойчивая система
3) 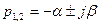
отрицательной вещественной частью
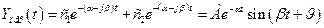
затухающие гармонические колебания

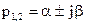
Неустойчивая система
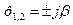

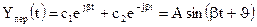 |
монотонный колебательный процесс
с постоянной частотой и амплитудой.
Система на границе устойчивости.
Вывод:Чтобы САУ была устойчивой необходимо, чтобы вещественные части корней были отрицательными. Если хотя бы один корень имеет положительную вещественную часть, то процесс будет расходящийся а система – неустойчива.
Если корень равен 0, то малейшее появление отрицательной составляющей сделает процесс устойчиво колебательным, а положительной – неустойчиво колебательным.
Часто корни характеристического уравнения при анализе устойчивости систем изображают на комплексной плоскости – плоскости корней характеристического уравнения
Комплексная плоскость мнимой осью разбивается на 2 части. Левую сторону называют областью устойчивости,а правую – областью неустойчивого движения.
Если корни лежат на мнимой оси или в 0, то система находится на границе устойчивости.
Вывод:Для устойчивости САУ необходимо и достаточно, чтобы все корни характеристического уравнения лежали слева от мнимой оси плоскости корней. Если хоть один корень справа, то система неустойчива. Таким образом, мнимая ось есть граница, за которую корни не должны переходить.
Если система имеет хотя бы один нулевой корень или хотя бы одну пару чисто мнимых корней, а все остальные корни имеют отрицательную вещественную часть, то система находится на границе устойчивости. При этом выделяют 3 типа границ устойчивости линейных систем:
1. Апериодическая граница устойчивости, которая соответствует р=0. Когда корень – нуль, то в характеристическом уравнении и система будет устойчива относительно скорости изменения управляемой величины, а сама управляющая величина может принимать произвольное значение. Система является нейтрально устойчивой.
2. Колебательная граница устойчивости, которой соответствуют чисто мнимые корни
В связи с тем, что корни характеристического уравнения определять трудно для систем высокого порядка, были разработан целый ряд критериев, с помощью которых судят об устойчивости систем.
Алгебраические критерии.
Критерий устойчивости Гурвица.
При рассмотрении алгебраических критериев используются лишь коэффициенты характеристического уравнения и необходимые и достаточные условия устойчивости систем.
Необходимое условие является справедливым для всех систем:
Все коэффициенты характеристического уравнения должны быть положительными
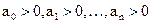
Для устойчивости линейной САУ по критерию Гурвица необходимо и достаточно, чтобы были положительными n главных определителей матрицы коэффициентов характеристического уравнения заданной системы (знаменатель передаточной функции):
Матрица коэффициентов
По диагонали от левого верхнего угла до правого нижнего выписывают все коэффициенты по порядку от а1 до аn. Каждая строка дополняется коэффициентами с возрастающими индексами слева направо так, чтобы чередовались строки с чётными и нечётными индексами. В случае отсутствия даннного коэффициента или если его индекс n, то на его место пишется 0.






0 




Если аn=0 , то имеет место апериодическая граница устойчивости.

Критерий Раусса.
Так же базируется на коэффициентах характеристического уравнения, из которого строится таблица.

| а0 | а2 | а4 | а6 | а8 |
| а1 | а3 | а5 | а7 | а9 |
| b1 | b2 | b3 | b4 | |
| c1 | c2 | c3 | … | … |
| … | … | … | … | … |
Для устойчивости системы все коэффициенты 1-го столбца должны быть больше 0
Частотные критерии
Критерий Михайлова.
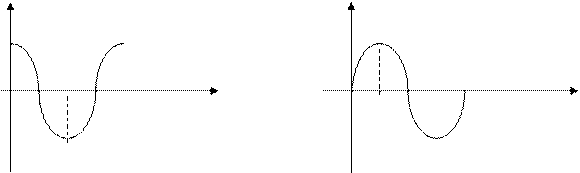
Критерий базируется на поведении кривой, которую описывает конец вектора (X(ω),Y(ω)) замкнутой системы при изменении частоты от 0 до + 
Возьмём характеристический полином следующего вида:
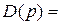
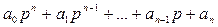
Подставим в него 
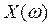
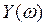
Изобразим годограф Михайловавыражения 
Берём значения 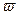

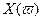
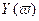
Формулировка критерия Михайлова.
Чтобы САР была устойчивой, необходимо и достаточно, чтобы вектор D(jω) при изменении частоты от 0 до +∞ начал движение с точки, лежащей на положительной вещественной оси, и, вращаясь только против часовой стрелки и нигде не обращаясь в нуль, прошел последовательно n квадрантов комплексной плоскости, повернувшись на угол n∙π/2, где n – степень характеристического уравнения D(jω)=0
Другими словами, требуется, чтобы кривая Михайлова проходила последовательно 

Устойчивая Неустойчивая Апериодическая Колебательная
граница устойчивости граница устойчивости
Другая формулировка критерия Михайлова:
Она состоит в использовании свойства перемежаемости корней многочленов 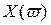

Идя по кривой Михайлова от т. 

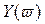

Это значит, что корни уравнений 

Кривые 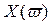

Перемежаться должны корни 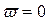

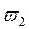
Условием устойчивости системы является перемежаемость корней полиномов вещественной и мнимой частей комплексной передаточной функции. Нарушение этого условия говорит о неустойчивости системы.
Видео:Теория автоматического управления. Лекция 8. Основы устойчивостиСкачать

Левые и правые корни характеристического уравнения
8.1. Понятие устойчивости системы
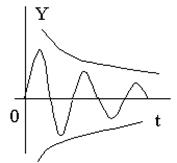
Под устойчивостью системы понимается способность ее возвращаться к состоянию установившегося равновесия после снятия возмущения, нарушившего это равновесие. Неустойчивая система непрерывно удаляется от равновесного состояния или совершает вокруг него колебания с возрастающей амплитудой.
Устойчивость линейной системы определяется не характером возмущения, а структурой самой системы (рис.61). Говорят, что система устойчива «в малом» , если определен факт наличия устойчивости, но не определены ее границы. Система устойчива «в большом» , когда определены границы устойчивости и то, что реальные отклонения не выходят за эти границы.
В соответствии с классическим методом решение дифференциального уравнения ищется в виде:
y(t) = y вын (t) + y св (t).
Здесь yсв(t) — общее решение однородного дифференциального уравнения , то есть уравнения с нулевой правой частью:
a o y (n) + a 1 y (n-1) + . + a (n-1) y’ + a (n) y = 0.
Физически это означает, что все внешние воздействия сняты и система абсолютно свободна, ее движения определяются лишь собственной структурой. Поэтому решение данного уравнения называется свободной составляющей общего решения. y вын (t) — частное решение неоднородного дифференциального уравнения , под которым понимается уравнение с ненулевой правой частью. Физически это означает, что к системе приложено внешнее воздействие u(t) . Поэтому вторая составляющая общего решения называется вынужденный . Она определяет вынужденный установившийся режим работы системы после окончания переходного процесса.
Можно провести аналогию между САУ и пружиной, колебания которой описываются аналогичным дифференциальным уравнением (рис.62). Оттянем пружину, а затем отпустим, предоставив ее самой себе. Пружина будет колебаться в соответствии со свободной составляющей решения уравнения, то есть характер колебаний будет определяться только структурой самой пружины. Если в момент времени t = 0 подвесить к пружине груз, то на свободные колебания наложится внешняя сила Р . После затухания колебаний, описываемых только свободной составляющей общего решения, система перейдет в новый установившийся режим, характеризуемый вынужденной составляющей y вын = y(t 



Каждая составляющая общего решения уравнения динамики ищется отдельно. Вынужденная составляющая ищется на основе решения уравнения статики для данной системы для времени t 





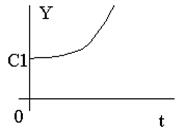
Каждому отрицательному вещественному корню соответствует экспоненциально затухающая во времени составляющая y св (t) i , каждому положительному — экспоненциально расходящаяся, каждому нулевому корню соответствует y св (t) i = const (рис.63). Пара комплексно сопряженных корней с отрицательной вещественной частью определяет затухающие колебания с частотой 
Так как после снятия возмущения y вын (t) = 0 , то устойчивость системы определяется только характером свободной составляющей y св (t) . zПоэтому условие устойчивости систем по Ляпунову формулируется так: в устойчивой системе свободная составляющая решения уравнения динамики, записанному в отклонениях, должна стремиться к нулю, то есть затухать.
Исходя из расположения на комплексной плоскости корни с отрицательными вещественными частями называются левыми , с положительными — правыми (рис.65).
Поэтому условие устойчивости линейной САУ можно сформулировать следующим образом: для того, чтобы система была устойчива, необходимо и достаточно, чтобы все корни ее характеристического уравнения были левыми. Если хотя бы один корень правый, то система неустойчива. Если один из корней равен нулю (в системах, где a n = 0 ), а остальные левые, то система находится на границе апериодической устойчивости . Если равны нулю вещественные части одной или нескольких пар комплексно сопряженных корней, то система находится на границе колебательной устойчивости .
Правила, позволяющие судить о знаках корней характеристического уравнения без его решения, называются критериями устойчивости . Их можно разделить на алгебраические (основаны на составлении по данному характеристическому уравнению по определенным правилам алгебраических выражений, по которым можно судить об устойчивости САУ) и частотные (основаны на исследовании частотных характеристик).
8.2. Алгебраические критерии устойчивости
8.2.1. Необходимое условие устойчивости
Характеристическое уравнение системы с помощью теоремы Виета может быть записано в виде
D(p) = a o p n + a 1 p n-1 + a 2 p n-2 + . + a n = a o (p-p 1 )(p-p 2 ). (p-p n ) = 0,
где p 1 , p 2 , . p n — корни этого уравнения. Если система устойчива, значит все корни левые, то есть вещественные части всех корней
отрицательны, что можно записать как a i = -|a i | . Подставим их в уравнение:
a 0 





Перемножая комплексно сопряженные выражения, получим:
a 0 



После раскрытия скобок должно получиться выражение
a 0 


Так как в скобках нет ни одного отрицательного числа, то ни один из коэффициентов a 0 ,a 1 . a n не будет отрицательным. Поэтому необходимым условием устойчивости САУ является положительность всех коэффициентов характеристического уравнения: a 0 > 0, a 1 > 0, . , a n > 0 . В дальнейшем будем рассматривать только уравнения, где a 0 > 0 . В противном случае уравнение домножается на -1.
Рассмотренное условие является необходиным, но не достаточным условием. Необходимые и достаточные условия дают алгебраические критерии Рауса и Гурвица.
8.2.1. Критерий Рауса
Раус предложил критерий устойчивости САУ в виде алгоритма, по которому заполняется специальная таблица с использованием коэффициентов характеристического уравнения:
1) в первой строке записываются коэффициенты уравнения с четными индексами в порядке их возрастания;
2) во второй строке — с нечетными;
3) остальные элементы таблицы определяется по формуле: c k,i = c k+ 1,i — 2 — ri

4) Число строк таблицы Рауса на единицу больше порядка характеристического уравнения.
Видео:3,5 способа отбора корней в тригонометрии | ЕГЭ по математике | Эйджей из ВебиумаСкачать

Левые и правые корни характеристического уравнения
Характер свободного движения всей системы при наличии различных корней определяется суммой свободных составляющих формулы (3.3.), причем система бывает устойчивой, если все вещественные корни отрицательные и комплексные корни имеют отрицательную вещественную часть. Если корни нанести на плоскость комплексного переменного, то можно выделить устойчивые, неустойчивые и нейтральные зоны.




Линейная САУ устойчива, если корни характеристического уравнения расположены слева от мнимой оси. Система считается нейтральной, если корни принадлежат мнимой оси.
Неустойчивой система считается для случая, когда корни лежат справа от мнимой оси.
Вышеперечисленные условия устойчивости используются для формулирования необходимого условия устойчивости линейных САУ.
Кроме выше записанного необходимое условие устойчивости можно записать, используя известное в математике выражение:
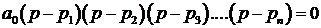
Подставив в выражение (3.6.) только устойчивые корни характеристического уравнения можно заметить, что после раскрытия скобок в уравнении (3.6.) устойчивой системы все коэффициенты характеристического уравнения будут положительными.
Необходимое условие устойчивости – положительность всех коэффициентов характеристического уравнения. В том случае, если один из коэффициентов отрицателен – линейную систему нельзя считать устойчивой.
Для уравнений первого и второго порядка условие положительности коэффициентов характеристического уравнения является кроме необходимого еще и достаточное условие. Это можно охарактеризовать тем, что уравнения первого и второго порядка просты для нахождения корней. Начиная с третьего и выше порядков характеристические уравнения трудно разрешить в нахождении корней простыми способами вычисления. Поэтому в теории автоматического управления разработаны упрощенные правила – критерии нахождения устойчивости линейных систем.
Существует два вида критериев: алгебраические и частотные. С математической точки зрения все рассматриваемые критерии равнозначны.
§ 3.2.3 Алгебраический критерий устойчивости. Критерий Рауса
Данный критерий устойчивости был разработан в 1878 г . английским математиком Раусом и который был сформулирован в виде некого правила или алгоритма, который можно представить в виде таблицы (матрицы).
Таблица Рауса составляется на основании характеристического уравнения линейной системы вида:
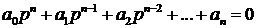
Покажем эту таблицу:
Порядок заполнения таблицы Рауса:
1) в первой строке таблицы Рауса в порядке увеличения индексов записываются коэффициенты характеристического уравнения (3.7), имеющие четный индекс: 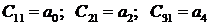
2) во второй строке записывают в порядке возрастания индексов коэффициенты характеристического уравнения (3.7.) с нечетными индексами: 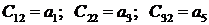
Любой из остальных коэффициентов таблицы Рауса записывается в соответствии со следующими выражениями:
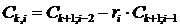
к – столбец, i – строка
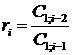
Число строк таблицы Рауса равно степени характеристического уравнения + 1 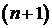
Условие устойчивости Рауса: для того, чтобы линейная САУ была устойчивой необходимо и достаточно чтобы коэффициенты первого столбца таблицы Рауса имели один и тот же знак, т.е. при 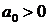
§ 3.2.4 Алгебраический критерий устойчивости. Критерий Гурвица
В 1895 г . немецкий математик Гурвиц разработал алгебраический критерий устойчивости в форме определителей, состоящих из коэффициентов характеристического уравнения (3.7).
В основе рассматриваемого критерия лежит построение главного определителя Гурвица из коэффициентов характеристического уравнения (3.7).
Порядок составления главного определителя Гурвица:
1. Записываем главную диагональ определителя Гурвица, составленную из коэффициентов характеристического уравнения от 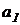
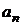
2. Вверх от главной диагонали записывают столбцы, составленные из коэффициентов характеристического уравнения с последовательно возрастающими индексами;
3. Вниз от главной диагонали записываем столбцы составленные из коэффициентов характеристического уравнения с последовательно убывающими индексами;
4. Оставшиеся пустые места определителя заполняются нулями, т.е. нули проставляются на места, где должны быть коэффициенты с индексами больше 0 и меньше 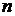
Главный определитель Гурвица имеет вид:
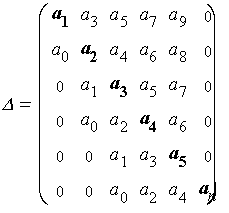 |
После построения главного определителя Гурвица, в нем очеркиваются диагональные миноры и тем самым получаются определители более низших порядков.

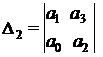
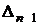
Критерий устойчивости Гурвица: для того, чтобы система автоматического управления (САУ) была устойчивой необходимо и достаточно, чтобы все определители Гурвица (3.11) имели знаки одинаковые со знаком первого коэффициента характеристического уравнения 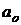
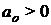
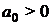
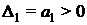
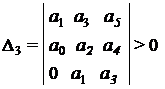
В случае, если хоть одно из условий не выполняется, то систему считают неустойчивой.
Раскрывая все определители Гурвица можно для уравнений 1-го, 2-го, 3-го и 4-го порядков записать более простую форму критерия устойчивости. Такая форма записи получила название следствия из критерия Гурвица или ее называют критерием Леера-Шепорда.
1) Для характеристического уравнения 1-го порядка:
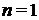
необходимым и достаточным является, чтобы:
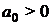
2) Для характеристического уравнения 2-го порядка:
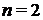
необходимым и достаточным является, чтобы:
3) Для характеристического уравнения 3-го порядка:
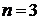
необходимым и достаточным является, чтобы:
4) Для характеристического уравнения 4-го порядка:
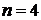
необходимым и достаточным является, чтобы:
§ 3.2.5 Частотный критерий устойчивости. Критерий Михайлова
Все частотные критерии, в том числе и критерий Михайлова, основаны на хорошо известном из курса высшей математики «Принципа аргумента», который позволяет отобразить необходимое условие устойчивости на частотной плоскости.
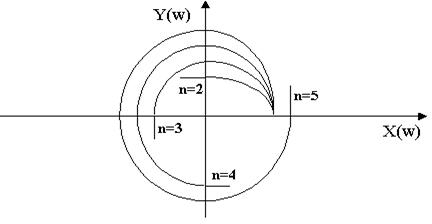
Все элементарные вектора 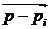

Этот частотный критерий устойчивости был сформулирован в 1938 г . советским ученым Михайловым и является интерпретацией принципа аргумента, позволяя судить об устойчивости системы наблюдая за поведением кривой называемой кривой Михайлова.
За основание построения кривой берется характеристический полином вида:
Произведя замену 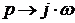
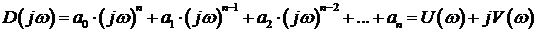
При изменении частоты 
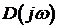
Для устойчивых систем кривая Михайлова начинаясь при 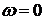

Критерий Михайлова: для того, чтобы САУ была устойчивой, необходимо и достаточно, чтобы кривая или годограф Михайлова при изменении 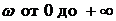
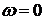
Нейтральные САУ (граница устойчивости):
Анализируя кривую Михайлова можно вывести следствие из него: при прохождении кривой Михайлова числа квадрантов комплексной плоскости, происходит последовательное поочередное пересечение действительной и мнимой соей, т.е.:
Значение частот при которых происходит пересечение кривой с вещественной или мнимой осью, должны является корнями уравнений (3.20) и (3.21), причем 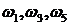
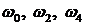
В связи с выше записанным следствие кривой Михайлова можно сформулировать следующим образом: САУ будет устойчивой тогда и только тогда, когда вещественная 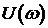
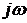
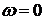
Для реализации этого следствия определяются только корни уравнения 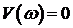
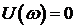
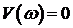
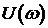
§ 3.2.6 Частотный критерий. Критерий Найквиста
Этот критерий разработан в 1923 г . американским ученым Найквистом. Он позволяет судить об устойчивости замкнутой системы по поведению АФЧХ разомкнутой системы.
Вектор 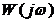

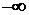
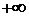
Кривая, описываемая окончанием этого вектора есть АФЧХ разомкнутой системы, причем следует отметить, что вид этой характеристики симметричен относительно начала координат, т.е.
Для доказательства критерия Найквиста используют дополнительную функцию вида:
Причем в знаменателе такой функции будет записан характеристический полином разомкнутой системы, а в числителе характеристический полином замкнутой системы:
В случае замены оператора Лапласа р на 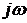
Пусть характеристическое уравнение замкнутой системы 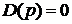
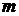
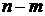
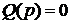
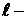
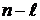
При рассмотрении этого критерия так же работает принцип аргумента, который определяет, что устойчивой система является, когда вектор 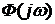
Разомкнутая система являющееся неустойчивой и имеющая 

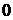
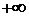
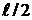
Найквистом было отмечено, что движение вектора 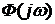
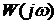
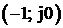
Критерий устойчивости Найквиста: если разомкнутая система автоматического управления неустойчива, то для того чтобы замкнутая система была устойчивой необходимо и достаточно, чтобы АФЧХ разомкнутой системы 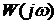

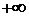
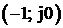
При сложной форме характеристик 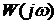
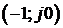
Для анализа поведения таких характеристик применяют «правило переходов» Ципкина. Назовем переход АФЧХ через действительную ось слева от точки 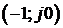

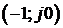
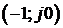
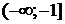
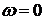
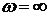
Критерий Найквиста для рассматриваемого варианта: если разомкнутая САУ неустойчива, то для того чтобы замкнутая система стала устойчива необходимо и достаточно, чтобы разность между положительным и отрицательным переходами АФЧХ разомкнутой системы через отрезок вещественной оси 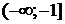

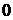
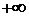
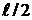
Критерий Найквиста для случая, когда разомкнутая система устойчива имеет следующую формулировку: если САУ разомкнутая устойчива, то замкнутая система будет устойчивой, если АФЧХ разомкнутой системы 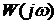
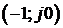
Достоинство критерия Найквиста заключается в том, что его можно использовать даже если неизвестны структуры отдельных звеньев системы, достаточно получить АФЧХ. Кроме того, рассматриваемый критерий позволяет анализировать устойчивость систем обладающих запаздыванием.
§ 3.2.7. Частотный критерий устойчивости – логарифмический частотный критерий
Критерий Найквиста позволяет судить от устойчивости системы по логарифмическим частотным характеристикам, т.е. можно заметить, что критерий Найквиста можно анализировать используя простые с точки зрения построения логарифмические частотные характеристики. Поэтому рассматриваемый критерий часто называют критерием Найквиста в логарифмической форме.
Передаточная функция разомкнутой системы обычно представляет собой произведение элементарных динамических звеньев, асимптотические характеристики которых представляют собой ломаные прямые линии.
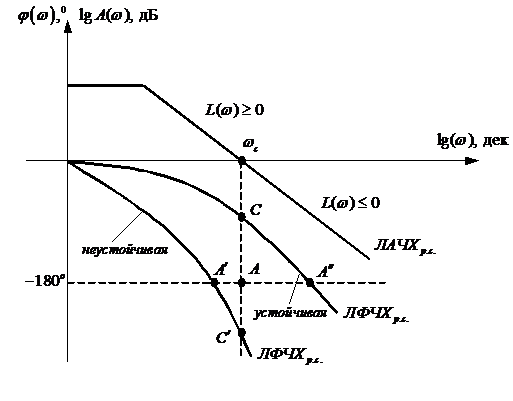
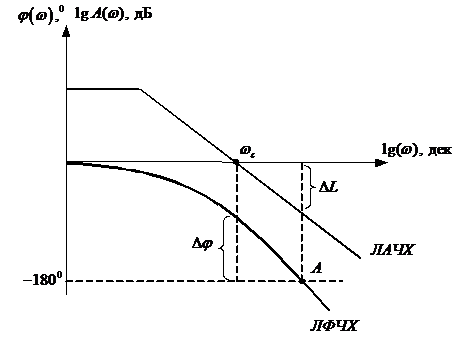
Устойчивость с использованием логарифмического критерия позволяет построив совмещено ЛАЧХ и ЛФЧХ разомкнутой системы судить об устойчивости замкнутой системы.
Замкнутая система автоматического управления устойчива, если при 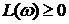
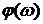
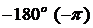
1) система устойчивая в разомкнутом состоянии будет устойчивой и в замкнутом, если точка А ЛФЧХ определяемая фазой 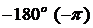
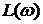
2) САУ неустойчивая в разомкнутом состоянии будет устойчива в замкнутой, если при изменении 
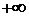
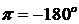
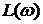
Следствие к первому случаю: САУ будет устойчивая в замкнутом состоянии, если ЛФЧХ неустойчивой разомкнутой системы при 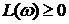
§ 3.2.8. Запасы устойчивости
При проектировании систем автоматики стремятся обеспечить их устойчивость с некоторой гарантией, чтобы изменение параметров системы в процессе ее работы не могли привести к неустойчивости системы. Для реализации такого тезиса необходимо, чтобы система обладала определенным запасом устойчивости. Запас устойчивости определяет удаленность параметров системы от границы устойчивости.
Положение системы на границе устойчивости можно определить, используя критерий устойчивости. Качественную характеристику удаления системы от границы устойчивости дают критерии Гурвица и Михайлова. Четкую количественную характеристику запаса устойчивости как по амплитуде, так и по фазе дает критерий Найквиста и логарифмический критерий.
В соответствии с критерием Найквиста система находится на границе устойчивости, если годограф Найквиста проходит через точку с координатами 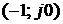
Покажем использование критерия Найквиста для нахождения запаса устойчивости по фазе и амплитуде:
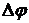
Запас устойчивости по модулю может быть в данном случае рассчитан как:
Значение модуля АФЧХ разомкнутой системы 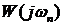
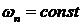
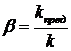
где 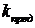
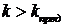
Запас устойчивости по фазе 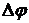
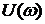
Определение устойчивости по логарифмическим частотным характеристикам может быть осуществлено достаточно простым способом. Необходимо на совмещенных логарифмических частотных характеристиках построить вертикальные проекции между осью абсцисс и значением -180º которые проведены через точки 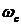
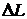
Запасы устойчивости влияют не только на работоспособность (устойчивость) системы, но также характеризуют качество работы системы. В реальных системах обычно 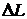
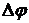
§ 3.2.9. Устойчивость систем обладающих запаздыванием
Значительное число объектов сельскохозяйственного назначения описываются математической моделью, в состав которой входит звено транспортного запаздывания, при этом общая передаточная функция такой системы состоит из произведения передаточной функции линейной части системы и передаточной функции звена транспортного запаздывания
Частотная передаточная функция в данном случае может быть записана в виде:
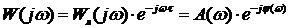
где 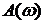
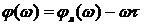
Звено чистого запаздывания не изменяет амплитуду АФЧХ, но создает дополнительный отрицательный сдвиг по фазе, зависящий от частоты 
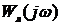
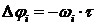
Оценку устойчивости систем с запаздыванием можно также выполнить используя логарифмический частотный критерий.
Очень часто анализируя устойчивость рассмотренных систем необходимо бывает установить значение запаздывания при котором система находится на границе устойчивости. Такое время носит название критического времени запаздывания и оно определяется из следующего выражения:
§ 3.3. Качества работы САУ
§ 3.3.1. Общие положения о качестве работы
Факт устойчивости или неустойчивости САУ говорит лишь о том, что переходная или свободная составляющая процесса регулирования с течением времени расходится или затухает, но такой анализ не дает ответа на такие важные вопросы как: быстрота затухания переходного процесса, форма кривой процесса регулирования и т.д. Поэтому следует отметить, что теория устойчивости является необходимым, но не достаточным условием практической пригодности САУ. Любая такая система кроме устойчивости должна еще обладать и требуемым качеством работы. Качество работы систем автоматики характеризует точность ее работы как в установившемся так и переходном режимах. Иными словами можно отметить, что качество работы системы автоматики характеризует точность воспроизведения системой задающего воздействия.
Проблема качества систем автоматики может быть поставлена как задача анализа, т.е. оценка уже спроектированной САУ или как задача синтеза, т.е. проектирование САУ заранее оговоренными показателями качества. При рассмотрении таких задач будем полагать, что САУ описывается системой дифференциальных уравнений с постоянными коэффициентами. При изменении воздействия 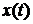
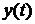
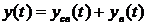
где 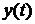
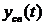
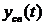
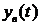
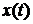
Качество работы системы автоматики можно оценить по виду переходного процесса и по его составляющим 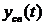
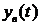
1) показатели качества переходного процесса 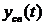
2) показатели качества, характеризующие вынужденную составляющую 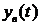
Показатели качества, определяемые непосредственно по кривой переходного процесса называют прямыми оценками качества, косвенные оценки качества не требуют нахождение кривой переходного процесса. Косвенные методы разделяют на: корневые, интегральные и частотные.
§ 3.3.2. Оценка качества регулирования при гармонических воздействиях
При гармонических воздействиях качество системы принято оценивать по амплитудо-фазовой, амплитудо-частотной и логарифмическим частотным характеристикам.
Для оценки качества переходных процессов системы можно использовать следующие величины: показатель колебательности М, резонансная (собственная частота) 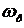
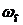
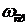
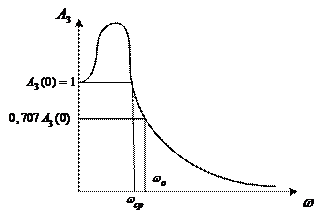
Показатель колебательности М – это отношение максимального значения АЧХ 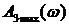
при 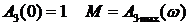
Показатель колебательности характеризует склонность системы к колебаниям. Чем выше М, тем менее качественная система при прочих равных условиях.
Частоту 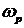
Полоса пропускания системы – это интервал частот от 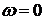
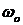
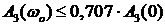
или при 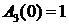
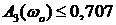
Частота среза 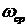
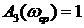
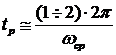
если переходный процесс имеет одно-два колебания, то время достижения переходной характеристикой первого максимума
Склонность системы к колебаниям характеризуется величинами ее запасов устойчивости по модулю и по фазе. Запасы устойчивости рассчитывают по АФЧХ и ЛЧХ. В хорошо демпфированных системах запас устойчивости по амплитуде колеблется в пределах от 6 до 20 дБ, а запас по фазе – от 30 до 60º.
Т.к. рассмотренные выше показатели косвенно определяют быстродействие, перерегулирование и т.п., то они могут быть использованы и для расчета систем, находящихся под воздействием непериодических возмущений.
🎬 Видео
УРАВНЕНИЕ В НАТУРАЛЬНЫХ! УСТНОЕ РЕШЕНИЕ 5-КЛАССНИКА!Скачать

АЛГЕБРА 9 класс: Целое уравнение и его корни | ВидеоурокСкачать

Решение систем уравнений. Методом подстановки. Выразить YСкачать

Теория автоматического управления. Лекция 9. Критерий ГурвицаСкачать

Теория автоматического управления. Лекция 12. D-разбиениеСкачать

15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

Асташова И. В. - Дифференциальные уравнения. Часть 2 - Фазовый портретСкачать

Решение системы линейных алгебраических уравнений (СЛАУ) в Excel МАТРИЧНЫМ МЕТОДОМСкачать

Задача 17 ЕГЭ профильный. Параметры с нуляСкачать

16. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентамиСкачать

Теория автоматического управления. Лекция 10. Критерий МихайловаСкачать

Решение системы уравнений в ExcelСкачать

5. Решение волнового уравнения на отрезке методом ФурьеСкачать

Свободное движение и устойчивость | Утро с теорией управления, лекция 2Скачать

3 класс. Математика. УравнениеСкачать

Видеоурок "Нахождение частных решений по виду правой части"Скачать

УМФ. Метод Фурье для параболического уравненияСкачать

Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать