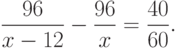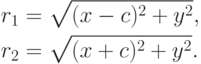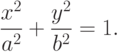Лекция решение уравнений и неравенств

Уравнения и неравенства

Один из основных вопросов, который «занимает» математиков — решение различных рода и типа уравнений или неравенств, систем уравнений (неравенств) или, как говорят математики, исследование уравнений на их разрешимость . Это выражение включает множество смежных аспектов — вывод уравнения (неравенства), нахождение решения, выяснение его однозначности, единственности и т.д. Нас будут интересовать два основных вопроса (как «нематематика») — вывод уравнения (неравенства) и нахождение его решения (хотя другие вопросы иногда могут оказаться не менее значимыми, интересными и сложными).

Уравнением называется некоторое определенное равенство, связывающее хотя бы один неизвестный объект (из некоторого, заранее определенного множества объектов) хотя бы с одним известным объектом из этого (чаще всего) или из другого множества.Если эти объекты — числового происхождения, то уравнение называется числовым (скалярным). Если объекты — векторы, то уравнение называется векторным. Если объекты — матрицы, то уравнение называется матричным и т.д.

Решением уравнения называется любое конкретное значение неизвестного объекта, которое при подстановке в уравнение превращает его в верное (истинное) равенство, то есть в тождество . Если такой допустимый объект не существует, то уравнение не имеет решения или неразрешимо в данном множестве объектов. Множество допустимых значений неизвестного объекта называется допустимым множеством решений или областью определения уравнения .

Количество известных и неизвестных объектов уравнения существенно влияет на разрешимость уравнения.

Пример. Уравнение 2x+3=7 — простое скалярное уравнение, относительно неизвестного числа x . Уравнение 2x+3y=z — также скалярное, но уже относительно трех неизвестных. Это уравнение — несравнимо более сложное и в общем виде не имеющее решения (то есть не имеющее метода, алгоритма поиска неизвестных x, y, z ).

Если решается уравнение вида f(x)=0 и найдено его решение x=a (иначе говоря, f(a)=0 ), то x=a называют нулем функции f(x) .

Неравенство — некоторое соотношение, связывающее неизвестный объект (неизвестные объекты) с известными объектами с помощью знаков неравенства (знаков , , , , > ).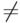

Неравенства, как и уравнения, могут быть различного типа: скалярные, векторные и т.д.

Решение системы уравнений (неравенств) должно обращать в тождество каждое уравнение ( неравенство ) системы. Для решения системы уравнений (неравенств) необходимо решить каждое уравнение ( неравенство ), найти множества решений каждого уравнения (неравенства) и взять их пересечение (то есть подмножество , где каждое уравнение или неравенство обращается в верное числовое равенство или неравенство ).

Решить уравнение ( неравенство ) означает найти все допустимые объекты, превращающие уравнение (неравенство) в истинное равенство (неравенство). Решением уравнения (неравенства) называют часто также и сам процесс нахождения таких объектов.

Пример. Получим (как говорят математики, «выведем») и затем решим скалярное уравнение (уравнение с числовым неизвестным) по следующим исходным данным ( по следующей содержательной постановке задачи): расстояние между станциями A и B по железной дороге равно 96 км, при этом первый поезд, идущий со средней скоростью на 12 км/час больше, чем второй, проходит это расстояние на 40 мин. быстрее, чем второй; необходимо найти скорости обоих поездов. Для получения уравнения проанализируем условие задачи и выпишем содержательно связь между параметрами (элементами) задачи, то есть выпишем содержательное уравнение вида (Время на AB второго поезда) — (Время на AB первого поезда) = 40 мин .

Теперь видно, что для нахождения неизвестных объектов (времени) этого уравнения необходимо ввести неизвестное — скорость (так как путь известен). Итак, обозначим через x (км/час) — скорость первого поезда, тогда скорость второго поезда будет по условию задачи равна x-12 (км/час). Из содержательно и не формализованно записанного соотношения, получаем уже формализованное, алгебраическое уравнение вида

Решаем это уравнение. Для этого приводим к общему знаменателю: .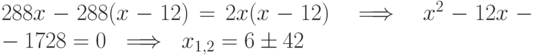

Отбрасывая затем один из неподходящих двух корней ( x=-36 ), получаем скорость первого поезда — 48 км/час, а скорость второго поезда (находим по условию задачи) — 36 км/час.

Особый класс уравнений и неравенств образуют уравнения и неравенства, связывающие текущие координаты точки на прямой , плоскости, пространстве и описывающие геометрические свойства, геометрическую (топологическую) структуру множества точек, удовлетворяющих такому соотношению, то есть решений таких уравнений или неравенств. Такие уравнения часто называют уравнениями линий, поверхностей (фигур, тел).

Рассмотрим некоторые основные, простые (канонические, как говорят в математике) типы таких уравнений и неравенств. Отметим попутно, что уравнения, определяющие линии на плоскости, часто в каноническом виде представлять не удается.

Окружность — это геометрическое место точек плоскости, отстоящих от некоторой фиксированной точки M(x₀; y₀) (называемой центром окружности) на одинаковом расстоянии r (называемой радиусом окружности). Задается неявным уравнением (x-x₀) 2 +(y-y₀) 2 =r 2 .

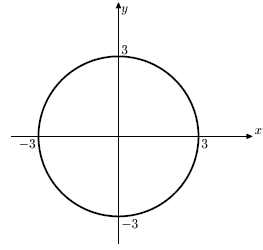
Пример. Уравнение окружности с центром в начале координат и радиусом, равным 3 единицы масштаба координатной системы, можно изобразить как на рис. 6.1.

Эллипс — это геометрическое место (рис. 6.2) точек M(x;y) , сумма расстояний от каждой из которых до двух данных точек F₁ и F₂ , называемых фокусами, есть величина постоянная.

Выведем уравнение эллипса. Пусть, согласно определению эллипса, r₁+r₂= | F₂M | + | F₁M | =2a .

Легко проверить ( по известной из школы формуле расстояния между двумя точками), что верны следующие равенства:

Поэтому из равенства r₁+r₂=2a получаем:

Это уравнение называется каноническим уравнением эллипса, величины r₁ и r₂ — фокальные радиусы точки M(x;y) , F₁, F₂ — фокусы эллипса, x=0 , y=0 — оси симметрии , величина 2a — большая ось, 2b — малая ось, 2c=| F₁F₂ | — фокусное расстояние , величина 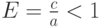— эксцентриситет эллипса.

Видео:Как понять неравенства? Квадратные неравенства. Линейные и сложные неравенства | TutorOnlineСкачать

Математическое пособие «Уравнения и неравенства»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Видео:Как решать неравенства? Часть 1| МатематикаСкачать

Математическое пособие

Видео:Как решать уравнения и неравенства? | Ботай со мной #072 | Борис Трушин |Скачать

Уравнения и неравенства

Видео:Решение квадратных неравенств | МатематикаСкачать

Методические указания

Видео:решение УРАВНЕНИЙ решение НЕРАВЕНСТВ 10 11 классСкачать

Пособие по данной теме, является наглядным, позволяет систематизировать знания учащихся. Все темы подробно разобраны (поэтапно). Материал служит как в качестве изучения темы с «нуля», так и в качестве вспомогательного материала. Включает в себя разобранные примеры, задания для самостоятельной работы (закрепления знаний).

Уравнения и неравенства– важнейшие понятия математики.

В большинстве практических и научных задач, где какую-то величину непосредственно нельзя измерить или вычислить по готовой формуле, удается составить соотношение, которым она удовлетворяет. Так получают уравнения и неравенства для определения неизвестных величины, которые каждый должен уметь решать.

Видео:Система уравнений VS Система неравенств. ОГЭ по математике №9, 13| Математика TutorOnlineСкачать

Решение уравнений и неравенств

Уравнение – это два выражения, соединенные знаком равенства; в эти выражения входят одна или несколько переменных, называемых неизвестными.

Значения переменных, которые обращают уравнение в верное числовое равенство, называются корнями или решениями уравнения. Решить уравнение – значит найти все его корни или установить, что корней нет.

Обычный путь решения уравнения состоит в том, что с помощью преобразований его сводят к более простым уравнениям.

Два уравнения называются равносильными , если каждое решение первого уравнения есть решение второго и наоборот, каждое решение второго есть решение первого. Перечислим преобразования, приводящие данное уравнение к равносильному ему уравнению:

Если к обеим частям уравнения прибавить одно и то же выражение, то получится уравнение, равносильное данному.

Если обе части уравнения умножить или разделить на одно и то же выражение, которое не обращается в нуль ни при каких значениях переменных, то получится уравнение, равносильное данному.

Уравнение с одной переменной называется линейным , если переменная входит в уравнение не выше, чем в первой степени.

Пример: 1) х +8( х –2)=2 х –3 – линейное уравнение;

2) х 3 – х 2 +3 х –4=–3 х +5 – не является линейным.

Стандартный вид линейного уравнения с одной переменной:

Для решения уравнения переносим слагаемое, не содержащее переменную вправо и делим обе части уравнения на коэффициент при неизвестном:

.

Для решения любого линейного уравнения нужно привести его к стандартному виду.

Пример: Решить уравнение:

Приведем уравнение к виду (*), для чего раскроем скобки и перенесем все члены уравнения влево

Приведем подобные члены

Перенесем слагаемое, не содержащее переменную вправо и поделим обе части уравнения на коэффициент при х , на (–3)

– 3 х =4  .

Ответ: .

Приведем уравнение к стандартному виду (*)

Перенесем слагаемое, не содержащее переменную вправо и поделим обе части уравнения на коэффициент при х на (–11)

 х =1.



приведем все дроби к общему знаменателю

Это уравнение не является линейным, но его можно свести к решению нескольких линейных уравнений. Разложим левую часть уравнения на множители, для чего сгруппируем 1-е и 2-е слагаемые и 3-е и 4-е слагаемые.

вынесем х из первого слагаемого и (–2) из второго

вынесем ( х 2 –1) за скобки

разложим первый сомножитель на множители, используя формулу разности квадратов

Произведение равно нулю, когда хотя бы одно из сомножителей равно нулю:

Таким образом, решение уравнения свелось к решению трех линейных уравнений, находим корень каждого из этих уравнений:

Рассмотрим пример решения уравнения с параметром (то есть уравнения, где коэффициенты при неизвестном могут принимать различные числовые значения и выражены буквами).

Здесь х – неизвестное, а – параметр.

Перенесем слагаемые, содержащие переменные влево, а слагаемые, не содержащие переменную, вправо

Следующий шаг при решении линейного уравнения: разделить обе части уравнения на коэффициент при неизвестном, но в нашем случае этот коэффициент зависит от параметра а, и может быть равен нулю, в такой ситуации делить на этот коэффициент нельзя, поэтому рассмотрим случай, когда коэффициент при неизвестном равен нулю отдельно.

а) Если а –2=0, то есть а =2, то уравнение принимает вид

и ни при каком значении х мы не получим верного равенства, следовательно в этом случае уравнение решений не имеет

б) Если а –2  0, то есть а  2, то поделим обе части уравнения на (а–2), получим

Таким образом мы получили:

Ответ: при а =2 решений нет;

при а  2 .

 Решить уравнение с параметром:

.

Так как в знаменателе дроби может стоять только выражение отличное от нуля, то

Уравнение имеет смысл, если а  2 и а  0. Решим уравнение при этих условиях. Приведем дроби к общему знаменателю

дробь равна нулю, когда числитель равен нулю, а знаменатель от нуля отличен

получили линейное уравнение с параметром а, относительно переменной х .

а) Если 3+ а =0, то есть а =–3, получим

и ни при каком х верного числового равенства мы не получим.

б) Если 3+ а  0, то есть а  –3, то

.

Ответ: при уравнение решений не имеет;

при .

2. Квадратные уравнения

Квадратным уравнением называют уравнение вида

Квадратное уравнение, в котором коэффициент при х 2 равен 1 называется приведенным.

Любое квадратное уравнение можно привести к приведенному, разделив обе части уравнения на коэффициент при х 2 , при этом полученное приведенное уравнение будет равносильно данному.

Пример: 3 х 2 –4 х +7=0  .

Для нахождения корней квадратного уравнения ах 2 + bx + с =0 пользуются формулами:

где D = b 2 –4 ac .

D называется дискриминантом квадратного уравнения, от его знака зависит число корней квадратного уравнения. Если:

D =0, – уравнение имеет один корень;

D >0, уравнение имеет два корня.

Пример: Решить уравнение.

В данном случае а =4, b =–7, с =3.

D = b 2 –4 ac =49–4  4  3=49–48=1>0  уравнение имеет два корня.

.

Ответ: .

Зная корни квадратного уравнения ax 2 + bx + c =0 можно разложить трехчлен, стоящий слева на множители. Если х ₁ , х ₂ – корни уравнения ax 2 + bx + c =0, то ax 2 + bx + c = a ( x – x ₁ )( x – x ₂ ), если квадратное уравнение имеет один корень x ₁ , то ax 2 + bx + c = а ( х – х ₁ ) 2 .

Корни приведенного квадратного уравнения x 2 + px + q =0 можно находить, используя теорему Виета :

Теорема: Сумма корней квадратного уравнения x 2 + px + q =0 равна коэффициенту при х , взятому с противоположным знаком; произведение корней равно свободному члену уравнения, то есть если x ₁ , x ₂ – корни уравнения, то

.

I способ . .

Найдем дискриминант квадратного уравнения

 уравнение имеет два корня, найдем их по формулам:

.

II способ . Умножим обе части первоначального уравнения на 3, получим приведенное квадратное уравнение, равносильное данному

Найдем корни квадратного уравнения, используя теорему Виета:

Если х ₁ , х ₂ – корни, то:

делителями числа 5 являются  1;  5, но только (–1) и (–5) в сумме дают (–6), поэтому х ₁ =–5; х ₂ =–1. Получили те же корни уравнения.

.

Приведем уравнение к стандартному виду, для чего перенесем все дроби с противоположным знаком влево, и приведем их к общему знаменателю

.

Дробь равна нулю, когда числитель равен нулю, а знаменатель от нуля отличен. Знаменатель этой дроби отличен от нуля при любых значениях х , поэтому приравняем к нулю числитель

.

Ответ: .

Рассмотрим примеры решения уравнений, которые квадратными не являются, но которые могут быть сведены к решению квадратных уравнений.

Перенесем все члены уравнения влево

слагаемые имеют одинаковые сомножители, вынесем одинаковые множители за скобку

Левая часть уравнения – есть произведение двух сомножителей, правая – нуль. Произведение равно нулю только в том случае, когда хотя бы один из множителей равен нулю. Таким образом, решение данного уравнения сводится к решению двух уравнений: линейного и квадратного:

х =2

.

Ответ: .

 .

Выражение, содержащее дробь имеет смысл, если знаменатель дроби отличен от нуля, поэтому 2 х –5  0  , х  0.

Приведем дроби к общему знаменателю

Дробь равна нулю, когда числитель равен нулю, знаменатель от нуля отличен. Мы уже выяснили условия, при которых знаменатель отличен от нуля, поэтому приравняем к нулю числитель дроби и решим квадратное уравнение.

(2 х ) 2 –2  2  5 х +(5) 2 =0

(2 х –5) 2 =0 

но при знаменатель дроби обращается в нуль, поэтому это значение переменной решением уравнения не является.

Ответ: решений нет.

 .

Найдем значения переменной, которые обращают в нуль знаменатель дроби, для чего решим уравнение

Разложим многочлен, стоящий слева на множители.

таким образом, имеем уравнение:

Произведение равно нулю только в том случае, когда хотя бы один из сомножителей равен нулю, поэтому уравнение сводится к решению двух уравнений:

 уравнение корней не имеет

таким образом, знаменатель дроби отличен от нуля при условии u  1.

Переходим к решению первоначального уравнения. Приравняем числитель дроби к нулю и решим квадратное уравнение.

решим приведенное уравнение, используя теорему Виета:

так как при u =1 знаменатель дроби обращается в нуль, решением уравнения будет только u =–2.

Линейные неравенства с одной переменной

Длина стороны прямоугольника 6 см. Какой должна быть длина другой стороны, чтобы периметр прямоугольника был меньше, чем периметр квадрата со стороной 4 см?

Решение: Если обозначить неизвестную сторону прямоугольника через х , то периметр прямоугольника будет равен: ( х +6)  2. Периметр же квадрата со стороной 4 см равен

По условию надо найти такие значения х , при которых ( х +6)  2>16.

Решение задачи свелось к решению неравенства, содержащего переменную. К решению неравенств приводят и многие другие задачи.

Решением неравенства с одной переменной называют значение переменной, которое обращает его в верное числовое неравенство.

Решить неравенство – это значит найти все его решения (или доказать, что их нет).

Неравенства называются равносильными , если множества их решений совпадают (неравенства, не имеющие решений также равносильны). При нахождении решений неравенств применяются утверждения, похожие на те, которыми мы пользовались при нахождении решений уравнений:

Решение неравенства не изменяется, если перенести какое-нибудь слагаемое в другую часть, изменив его знак на противоположный.

Решение неравенства не изменится, если умножить обе части этого неравенства на одно и то же положительное число; при умножении обеих частей неравенства на отрицательное число надо поменять знак неравенства на противоположный.

Используя это утверждение, решим полученное в задаче неравенство.

Ответ: длина стороны прямоугольника должна быть больше 2.

Рассмотрим примеры решения други х неравенств.

.

Ответ:

Ответ: .

 Найти все значения а , при которых квадратное уравнение: (2 а –1) х 2 +2 х –1=0 имеет два действительных различных корня.

Решение: Квадратное уравнение имеет два различных действительных корня, когда дискриминант уравнения больше нуля. Вычислим дискриминант уравнения и потребуем, чтобы он был больше нуля.

решим полученное неравенство

таким образом, уравнение имеет два различных действительных корня при .

Несколько неравенств с одной переменной образуют систему , если ставится задача найти все числа, каждое из которых является решением каждого из указанных неравенств. Неравенства, образующие систему, объединяются фигурной скобкой.

Например:

Несколько неравенств с одной переменной образуют совокупность , если ставится задача найти все числа, каждое из которых является решением хотя бы одного из заданных неравенств. Неравенства, образующие совокупность, обычно объединяются квадратной скобкой.

Например:

Чтобы найти решение системы неравенств нужно найти общую часть промежутков, которые являются решениями неравенств системы.

Н
анесем полученные решения на числовую ось и выберем пересечение всех трех промежутков.

Общей частью всех трех промежутков является промежуток .

Ответ: .



Решением первого неравенства является вся числовая ось, поэтому

Ответ: .

Задания для самостоятельного решения

1. Найдите все значения а , при которы х квадратное уравнение ( а –1) х 2 –(2 а +3) х + а +5=0 имеет действительные корни.

Решить системы неравенств:

2. 3.

Видео:Как решать неравенства? Математика 10 класс | TutorOnlineСкачать

Лекция по теме «Неравенства»

Лекция по теме «Неравенства»

1. Решение неравенств

2. Решение целых рациональных неравенств

3. Решение дробно-рациональных неравенств

4. Неравенства, содержащие знак модуля

5. Иррациональные неравенства

6. Уравнения и неравенства с параметрами

7. Графический метод решения задач с параметрами

1. Решение неравенств

Пусть функции и определены на некотором множестве . Поставим задачу: найти множество , на котором значения одной из функций больше (меньше) значений другой из них, другими словами, найти все значения , для которых выполняется неравенство: > (

💡 Видео

ЛИНЕЙНЫЕ УРАВНЕНИЯ - Как решать линейные уравнения // Подготовка к ЕГЭ по МатематикеСкачать

Что такое параметр? Уравнения и неравенства с параметром. 7-11 класс. Вебинар | МатематикаСкачать

Равносильность уравнений и неравенств. Видеоурок 7. Алгебра 10 классСкачать

Решение неравенства методом интерваловСкачать

Урок 10. Сложные уравнения и неравенства. Решение уравнений высоких степеней. Вебинар | МатематикаСкачать

Показательные и логарифмические уравнения | Подготовка к ЕГЭ по математике 2024Скачать

11 класс, 29 урок, Уравнения и неравенства с модулямиСкачать

Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

Решение квадратных неравенств методом интервалов. 8 класс.Скачать

Графический способ решения уравнений и неравенств | Алгебра 10 классСкачать

ПРОСТЕЙШИЙ способ решения Показательных УравненийСкачать

Алгебра 9. Урок 7 - Неравенства. Метод интервалов - основные фактыСкачать

Подготовка к ОГЭ . Рациональные неравенства | Математика | TutorOnlineСкачать