Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Рабочие листы и материалы для учителей и воспитателей
Более 300 дидактических материалов для школьного и домашнего обучения
Методы решения систем линейных алгебраических уравнений. Метод Гаусса
Цель работы: получение навыков численного решения линейных уравнений методом Гаусса
Метод Гаусса является одним из наиболее распространенных прямых методов решения систем линейных алгебраических уравнений. В основе метода лежит идея последовательного исключения неизвестных.
Рассмотрим систему из трех уравнений с тремя неизвестными:
Решение . Прямой ход исключения : Удалить члены с X1 из 2-го и 3-го уравнений можно, вычитая из 2-й строки 1-ую, умноженную на 2 , а из 3-й — первую, умноженную на 3:
Пример 2. Решить систему уравнений методом Гаусса с помощью программы на языке VBA Excel :
Ввести матрицу A и вектор B в рабочий лист Excel (рис.1).
Рисунок 1 – Решение системы линейных уравнений методом обратной матрицы с помощью программы Excel
2) Ввести код программы (рис.2) в модуль листа. В качестве значения переменной n указать число уравнений.
3) Выполнить программу. В столбце Н содержится решение системы:
Х 1 = 1,767019 1 ; Х 2 = 9,807512 2; Х 3 = 2,702465 3; Х 4 = — 0,48533 4 .
Рисунок 2 – Программа решения системы линейных алгебраических уравнений методом Гаусса на языке VBA
II . Практическая часть
Задание 1 . Решить систему уравнений методом Гаусса
- Краткое описание документа:
- Охрана труда
- Пожарная безопасность
- Охрана труда
- Дистанционные курсы для педагогов
- Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
- Другие материалы
- Вам будут интересны эти курсы:
- Оставьте свой комментарий
- Автор материала
- Дистанционные курсы для педагогов
- Подарочные сертификаты
- Мусихин 1 лаба, 15 вариант. Отчет по лабораторной работе 1 Решение системы линейных уравнений методом Гаусса на пэвм
- Метод Гаусса с выбором главного элемента
- 🎥 Видео
Краткое описание документа:
Методы решения систем линейных алгебраических уравнений. Метод Гаусса
Цель работы: получение навыков численного решения линейных уравнений методом Гаусса
Метод Гаусса является одним из наиболее распространенных прямых методов решения систем линейных алгебраических уравнений. В основе метода лежит идея последовательного исключения неизвестных.
Рассмотрим систему из трех уравнений с тремя неизвестными:
Решение . Прямой ход исключения : Удалить члены с X1 из 2-го и 3-го уравнений можно, вычитая из 2-й строки 1-ую, умноженную на 2 , а из 3-й — первую, умноженную на 3:
Пример 2. Решить систему уравнений методом Гаусса с помощью программы на языке VBA Excel :
Ввести матрицу A и вектор B в рабочий лист Excel (рис.1).
Рисунок 1 – Решение системы линейных уравнений методом обратной матрицы с помощью программы Excel
2) Ввести код программы (рис.2) в модуль листа. В качестве значения переменной n указать число уравнений.
3) Выполнить программу. В столбце Н содержится решение системы:
Х 1 = 1,767019 1 ; Х 2 = 9,807512 2; Х 3 = 2,702465 3; Х 4 = — 0,48533 4 .
Рисунок 2 – Программа решения системы линейных алгебраических уравнений методом Гаусса на языке VBA
II . Практическая часть
Задание 1 . Решить систему уравнений методом Гаусса
Курс повышения квалификации
Охрана труда
- Сейчас обучается 140 человек из 48 регионов
Курс профессиональной переподготовки
Пожарная безопасность
- Сейчас обучается 131 человек из 45 регионов
Курс профессиональной переподготовки
Охрана труда
- Сейчас обучается 251 человек из 56 регионов
«Мотивация здорового образа жизни. Организация секций»
Свидетельство и скидка на обучение каждому участнику
- Для всех учеников 1-11 классов
и дошкольников - Интересные задания
по 16 предметам
«Как закрыть гештальт: практики и упражнения»
Свидетельство и скидка на обучение каждому участнику
Видео:Математика без Ху!ни. Метод Гаусса.Скачать

Дистанционные курсы для педагогов
Самые массовые международные дистанционные
Школьные Инфоконкурсы 2022
33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 840 974 материала в базе
Ищем педагогов в команду «Инфоурок»
Другие материалы
- 19.05.2018
- 513
- 0
- 19.05.2018
- 1225
- 17
- 19.05.2018
- 775
- 11
- 19.05.2018
- 712
- 13
- 19.05.2018
- 384
- 3
- 19.05.2018
- 447
- 2
- 19.05.2018
- 473
- 0
- 19.05.2018
- 401
- 0
«Учись, играя: эффективное обучение иностранным языкам дошкольников»
Свидетельство и скидка на обучение
каждому участнику
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 19.05.2018 1961
- DOCX 9 мбайт
- 16 скачиваний
- Оцените материал:
Настоящий материал опубликован пользователем Басова Валентина Ивановна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 6 лет и 3 месяца
- Подписчики: 2
- Всего просмотров: 43978
- Всего материалов: 19
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Видео:Решение системы линейных уравнений методом ГауссаСкачать

Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Минпросвещения рекомендует школьникам сдавать телефоны перед входом в школу
Время чтения: 1 минута
Российские школьники начнут изучать историю с первого класса
Время чтения: 1 минута
С 1 сентября в российских школах будут исполнять гимн России
Время чтения: 1 минута
Минобрнауки отменило плановые и внеплановые проверки вузов в 2022 году
Время чтения: 1 минута
В Госдуме предложили унифицировать школьные программы
Время чтения: 1 минута
Вузы РФ не будут повышать стоимость обучения на первом курсе
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Видео:Решение системы уравнений методом ГауссаСкачать

Мусихин 1 лаба, 15 вариант. Отчет по лабораторной работе 1 Решение системы линейных уравнений методом Гаусса на пэвм
| Название | Отчет по лабораторной работе 1 Решение системы линейных уравнений методом Гаусса на пэвм |
| Дата | 05.12.2021 |
| Размер | 215.89 Kb. |
| Формат файла |  |
| Имя файла | Мусихин 1 лаба, 15 вариант.docx |
| Тип | Отчет #292667 |
| Подборка по базе: Стат отчет ШСП 21 год.docx, Готовый Отчёт по УП 06 Иванова А A. .docx, Комментарий к практической работе 2 (1).doc, методические указания к контрольной работе.docx, общий отчет.docx, Особенности использования ЭО, ДОТ. Отчет. Морина С.А..docx, 1 Тест. Реализация требований обновленных ФГОС НОО, ФГОС ООО в , Аналитический отчет НОВЫЙ.docx, Отчет по последней работе.docx, меры безопастности при работе с ядовитыми жидкостями.docx МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТТВЕННОЕ АВТОНОМНОЕ ОБРАЗРВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО «ЮЖНО-УРАЛЬСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ» (НАЦИОНАЛЬНЫЙ ИСЛЕДОВАТЕЛЬСКИЙ УНИВЕРСИТЕТ) Институт «Архитектурно-строительный» по лабораторной работе №1 «Решение системы линейных уравнений методом Гаусса на ПЭВМ» «Численные методы расчета строительных конструкций» 15 вариант ___________/ Мусихин В.А./ ___________________ 2019 г. Выполнил студент АСИ-371: ___________/ Кукушкин К.Е./ ___________________ 2019 г. Лабораторная работа № 1 P1=6kH; φ=45° (sin φ = cos φ = 0,707); P2=5,5kH; α=30° (sin α = 0,5;cos α = 0,866); q=1,5kH/м; W – число степеней свободы; Д – число дисков; С – число связей; Т.к. число степеней свободы равно нулю , система является статически определимой. Требуется определить опорные реакции балки ХА, YA, RB, YC, YD.
4. Преобразование системы в матричную форму 5. Блок-схема программы 6. Текст программ решения системы уравнений методом Гаусса и исходных данных на алгоритмическом языке «QBASIC» Файл nxm.dat – 5 (с первой позиции с первой строки) 4,595 13,395 59,296 -21,11 -47,279 20 DIM a(10, 10), b(10), x(10) 30 OPEN «nxm.dat» FOR INPUT AS #1 40 OPEN «axm.dat» FOR INPUT AS #2 50 OPEN «bxm.dat» FOR INPUT AS #3 60 OPEN «resultm.dat» FOR OUTPUT AS #4 70 PRINT #4, «Решение СЛАУ методом Гаусса « 80 PRINT #4, «Кукушкин К.Е., AC-371, вариант 15» 100 PRINT #4, «Размерность СЛАУ n=5» 110 PRINT #4, «Матрица констант при переменных А:» 120 FOR i = 1 TO n 130 FOR j = 1 TO n 140 INPUT #2, a(i, j) 150 PRINT #4, a(i, j); 180 PRINT #4, «Матрица свободных членов В:» 190 FOR i = 1 TO n 230 FOR k = 1 TO n — 1 250 max = ABS(a(k, k)) 260 FOR i = k + 1 TO n 270 IF max >ABS(a(i, k)) GOTO 300 290 max = ABS(a(i, k)) 310 IF m = k GOTO 400 320 FOR j = k TO n 400 FOR i = k + 1 TO n 410 d = a(i, k) / a(k, k) 420 FOR j = k + 1 TO n 430 a(i, j) = a(i, j) — d * a(k, j) 450 b(i) = b(i) — d * b(k) 480 x(n) = b(n) / a(n, n) 490 FOR i = n — 1 TO 1 STEP -1 510 FOR j = i + 1 TO n 520 s = s + a(i, j) * x(j) 540 x(i) = (b(i) — s) / a(i, i) 560 PRINT #4, «Величиныпеременных:» 570 FOR i = 1 TO n 580 PRINT #4, «X(«, i, «)=», X(i) 7.Решение системы уравнения на ПК Решение СЛАУ методом Гаусса Кукушкин К.Е., AC — 371, вариант 15 Размерность СЛАУ n = 5 Матрица констант при переменных А: Матрица свободных членов В: 4,595 13,395 59,296 -21,11 -47,379 8. Проверка правильности решения 1) 10,981 – 12,770 * 0.5 = 4,595 10,981 – 6,385 = 4,595 2) 1,507 + 12,770 * 0,866 – 3,239 + 4,067 = 13,395 1,507 + 11,058 – 3,239 + 4,067 = 13,395 3) 4 * 12,770 * 0,866 + 6,4 * (-3,239) + 8,8 * 4,067 = 59,296 44,235 – 20,729 + 35,789 = 59,296 4) – 5,9 * 1,507 – 12,770 * 0,866 * 1,2 = – 21,11 – 8,891 – 13,270 = – 21,11 – 21,11 = – 21,11 – 11,905 – 39,811 + 3,886 = – 47,379 Вывод: после решения системы уравнений методом Гаусса делается проверка правильности решения. Проверка сходится, следовательно, система линейных алгебраических уравнений решена правильно. Видео:Решение системы линейных алгебраических уравнений (СЛАУ) в Excel МАТРИЧНЫМ МЕТОДОМСкачать  Метод Гаусса с выбором главного элементаМосковский Государственный Технически Университет «МАМИ» Лабораторная работа №3 по курсу «Вычислительная Математика» «РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ» 3. РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ Справочная информация Численные методы решения систем линейных алгебраических уравнений записываемых в матричной форме в виде делятся на точные и итерационные. Они используются для систем, у которых количество неизвестных равно количеству уравнений и матрица A — не вырождена (её определитель не равен нулю). Точными методами условно называют методы, которые дают решение задачи посредством конечного числа арифметических операций. Итерационные методы позволяют получить решение системы как предел бесконечной последовательности его приближений. При применении итерационных методов существенным вопросом является вопрос об их сходимости. Точные методы, к которым относятся метод Гауссаи его разновидности, не имеют дополнительных ограничений на свойства матрицы системы. В основе метода Гаусса лежит идея последовательного исключения неизвестных, приводящая исходную систему с квадратной матрицей к легко разрешимой системе с верхней треугольной матрицей Данное преобразование может быть осуществлено многими способами. Однако все они основаны на свойстве систем, которое заключается в неизменности их решений при умножении любого уравнения на отличную от нуля постоянную или его замене на сумму с любым другим уравнением. Один из простейших способов исключения состоит в следующем. Первое уравнение системы которое на этом шаге считается ведущим, нормируется – делится на значение диагонального элемента a11 Если в исходной системе a11= 0, то в качестве первого уравнения следует взять любое другое с ненулевым первым коэффициентом, поменяв их местами. Полученное уравнение умножается на первый коэффициент второго уравнения a21 и вычитается из него. В результате во втором уравнении пропадает слагаемое a21x1, содержащее первое неизвестное x1. Такие же операции проводятся со всеми последующими уравнениями. В результате система уравнений принимает вид Далее процесс повторяется. За ведущее берется второе уравнение и исключается неизвестное x2 из всех уравнений, начиная с третьего Таким образом, за n шагов система уравнений последовательно сводится к треугольному виду, при этом для последнего уравнения выполняется только операция нормирования: Полученная система с верхней треугольной матрицей может быть легко разрешена относительно неизвестных. Последнее уравнение системы определяет значение xn, что позволяет определить xn–1 из предпоследнего уравнения как Выполняя аналогичные подстановки найденных неизвестных в вышестоящие уравнения, удается определить все компоненты решения xn–2. x2, x1. Метод Гаусса даёт точное решение, если все исходные данные точны и все вычисления производятся точно. На практике, при выполнении вычислений, неизбежно проводятся округления. Ошибка округлений вносит погрешность в решение метода Гаусса. Таким образом, при операциях с округленными десятичными числами метод Гаусса даёт не точное решение xт системы линейных алгебраических уравнений, а некоторое приближённое решение Степень отличия приближённого решения от точного определяется длиной разрядной сетки ЭВМ: чем больше разрядов в ней учитывается, тем это отличие меньше. При определении погрешности вектора решения необходимо учитывать, что его компоненты в общем случае могут иметь разную погрешность. В силу этого погрешность решения принято оценивать по его норме где двойные модульные скобки Для определения величины погрешности полученного решения а затем посредством повторного решения системы уравнений находится вектор погрешностей так и его относительная погрешность Величина погрешности решения системы уравнений, получаемого методом Гаусса, зависит от двух основных факторов. Первый из них, как это было сказано выше – длина разрядной сетки, используемой в процессе вычислений, а второй – обусловленность матрицы системы. Обусловленность матрицы можно рассматривать как степень её чувствительности к накоплению ошибок округления в процессе преобразований. Снижение величины погрешности решения может быть достигнуто увеличением длины разрядной сетки. Повлиять на величину погрешности посредством изменения степени обусловленности матрицы системы невозможно, так как она является одной из её характеристик и изменение степени обусловленности матрицы требует изменения самой матрицы. Метод Гаусса с выбором главного элемента Основное накопление погрешностей решения в методе Гаусса происходит на этапе приведения системы к треугольному виду. Механизм накопления основной части этой погрешности заключается в привнесении погрешностей вычисления коэффициентов ведущего уравнения в коэффициенты последующих уравнений при исключении каждого очередного неизвестного. Анализ соотношений метода Гаусса показывает, что погрешности вычисления коэффициентов ведущего уравнения привносятся в соответствующие коэффициенты всех последующих уравнений в долях отношений этих коэффициентов к диагональному (главному) коэффициенту ведущего уравнения. В связи с этим привносимая погрешность будет тем меньше, чем меньше доли этих отношений. Поэтому в методе Гаусса с выбором главного элемента на каждом шаге исключения i-го неизвестного в качестве ведущего используетсяуравнение (с i-го по n-ое), содержащее максимальный по модулю коэффициент – главныйэлемент. При этом в качестве него может использоваться один из коэффициентов i-го столбца, i-ой строки или всей непреобразованной части матрицы. Первый подход называется выбором главного элементапостолбцу, второй – по строке, а третий – по всейматрице. При использовании двух последних происходит перестановка столбцов матрицы системы. Это приводит к изменению порядка следования компонент вектора неизвестных и требует его восстановления по окончании процесса решения. В качестве примера применения метода Гаусса можно рассмотреть задачу отыскания решения следующей системы уравнений при ограничении разрядной сетки вычислений до трёх знаков и с оценкой погрешности получаемого решения. Поставленная задача будет решаться методом Гаусса с выбором главного элемента по столбцу. а. Выбор главного элемента среди элементов первого столбца б. Нормировка первого уравнения в. Исключение элементов первого столбца г. Выбор главного элемента среди элементов второго столбца второго и третьего уравнений д. Нормировка второго уравнения е. Исключение элементов второго столбца ё. Нормировка последнего уравнения В итоге получено решение системы уравнений 3. Погрешность найденного решения. а. Пересчёт вектора правых частей системы б. Формирование системы уравнений, определяющей погрешности решения в. Решение системы относительно погрешностей оно выполняется аналогично пунктам 1 и 2. Прямой ход (пункт 1) даёт следующую систему с верхней треугольной матрицей а обратный ход позволяет получить решение г. Оценка абсолютной и относительной погрешностей решения системы линейных алгебраических уравнений Реализация описанного метода без нахождения погрешности решения в рамках программы Excel приведена на рис.1. О выборе метода решения систем уравнений Каждый из рассмотренных методов имеет свои достоинства и недостатки. В частности, метод Гаусса позволяет получить решение за конечное число шагов. Для этого требуется выполнить n(n 2 + 3n – 1)/3 операций умножения и деления и n(n – 1)(2n + 5)/6 операций сложения и вычитания, количество которых при больших порядках системы (n > 100) можно принять равным n 3 /3 в обоих случаях. Однако его методические ошибки, связанные с размером разрядной сетки вычислений, резко нарастают с увеличением порядка системы и не позволяют применять его для систем высоких порядков без использования специальных приёмов. Итерационные методы позволяют получать решение систем бóльшего порядка. Для выполнения каждой итерации с их помощью необходимо выполнить n(n + 1) операций умножения и деления и столько же операций сложения и вычитания. При больших порядках системы уравнений (n > 100) их количество можно принять равным n 2 . Из сравнения трудоёмкости итерационных методов и метода Гаусса следует оценка, которой можно руководствоваться при окончательном выборе метода решения системы при необходимости его многократного нахождения. Если количество итераций, требуемое для получения решения системы итерационными методами, не превышает n/3, то выгоднее применять их, а не методы типа Гаусса. Однако здесь следует помнить, что итерационные методы требуют, чтобы матрица системы обладала определёнными свойствами, обеспечивающими их сходимость. Необходимо также отметить, что выполнение этих требований часто не гарантирует высокой скорости их сходимости. 🎥 Видео12. Решение систем линейных уравнений методом ГауссаСкачать  Решение системы уравнений методом Гаусса 4x4Скачать  СЛУ Метод Гаусса в ExcelСкачать  Математика это не ИсламСкачать  Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать  Метод Гаусса решения систем линейных уравненийСкачать  Метод Гаусса для решения систем линейных алгебраических уравненийСкачать  МЕТОД ПОДСТАНОВКИ 😉 СИСТЕМЫ УРАВНЕНИЙ ЧАСТЬ I#математика #егэ #огэ #shorts #профильныйегэСкачать  Система линейных уравнений. Общее решение. Метод ГауссаСкачать  Линейная алгебра, Матрицы: Метод Гаусса. Высшая математикаСкачать  Решение систем линейных уравнений, урок 4/5. Метод ГауссаСкачать  Общее, частное, базисное решение системы линейных уравнений Метод ГауссаСкачать  День студента мехмата МГУ #мгу #умскул #физика #математика #учеба #подготовкаогэ #подготовкакегэСкачать  решение системы уравнений методом ГауссаСкачать  СИСТЕМЫ УРАВНЕНИЙ В ЕГЭ ЧАСТЬ I #shorts #математика #егэ #огэ #профильныйегэСкачать  метод Гаусса СИСТЕМА ЛИНЕЙНЫХ УРАВНЕНИЙ решение СЛАУСкачать  |
















 a=b=c=d=2 м;e=f=g=h= l =1,3м;
a=b=c=d=2 м;e=f=g=h= l =1,3м;




 3. Преобразование системы в стандартную форму
3. Преобразование системы в стандартную форму









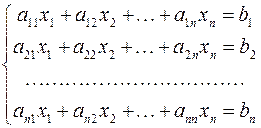 ,
, ,
,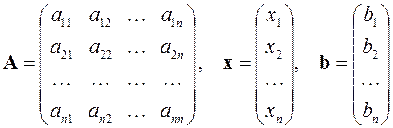 ,
, .
. ,
,
 ,
,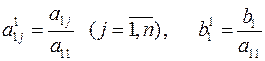 .
. .
. .
. .
. .
. , где
, где ,
,  .
. или
или 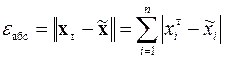 или
или ,
, обозначают норму вектора.
обозначают норму вектора. ,
,
 . С его помощью определяется как реальная абсолютная погрешность полученного решения
. С его помощью определяется как реальная абсолютная погрешность полученного решения или
или  или
или  ,
, .
.
 .
. .
. .
.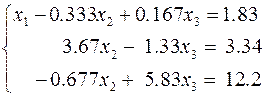 .
. .
. .
. .
.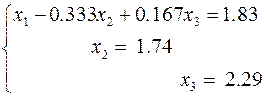 ,
, .
. .
.
 ,
,
 ,
, .
. ,
,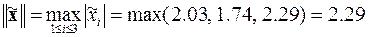 ,
, .
.