ЛАБОРАТОРНАЯ РАБОТА № 3
Тема: Решение систем линейных уравнений, работа с матрицами
Цель работы: Изучение возможностей пакета Ms Excel при решении задач линейной алгебры. Приобретение навыков решения систем линейных алгебраических уравнений и выполнение действий над матрицами средствами пакета.
Предварительно вспомним некоторые сведения из курса высшей математики, необходимые для выполнения данной лабораторной работы.
Решение систем линейных алгебраических уравнений (СЛАУ).
Пусть задана СЛАУ следующего вида:
Эту систему можно представить в матричном виде: AX=b, где

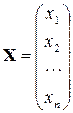
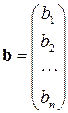
При выполнении лабораторной работы систему линейных алгебраических уравнений необходимо будет решать методом обратной матрицы и методом Крамера. Вспомним основные формулы, используемые в этих методах.
Метод обратной матрицы.
Систему линейных алгебраических уравнений Ax=b умножим слева на матрицу, обратную к А. Система уравнений примет вид:
A -1. A . x=A -1. b, E . x=A -1. b,(E – единичная матрица)
Таким образом, вектор неизвестных вычисляется по формуле x=A -1. b.
В этом случае неизвестные x1,x2,…, xn вычисляются по формуле:
где D – определитель матрицы A, Di – определитель матрицы, получаемой из матрицы А путем замены i-го столбца вектором b.
Обратите внимание на особенность работы с матричными формулами: необходимо предварительно выделять область, в которой будет храниться результат, а после получения результата преобразовывать его к матричному виду, нажав клавиши F2 и Ctrl+Shift+Enter.
Теперь рассмотрим решение системы линейных уравнений методом обратной матрицы и методом Крамера на следующих примерах.
ПРИМЕР 3.1. Решить систему методом обратной матрицы:
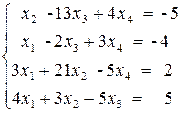
В этом случае матрица коэффициентов А и вектор свободных коэффициентов b имеют вид:
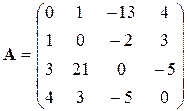
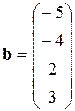
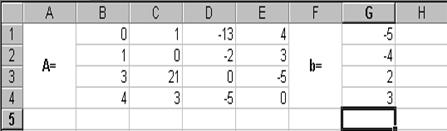
Введём матрицу A и вектор b в рабочий лист MS Excel (рис. 3.1).
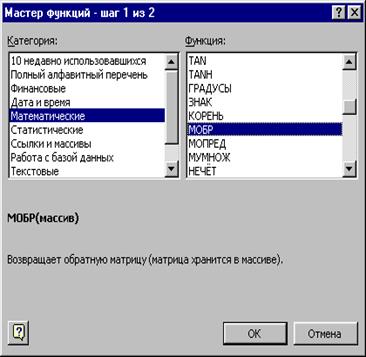
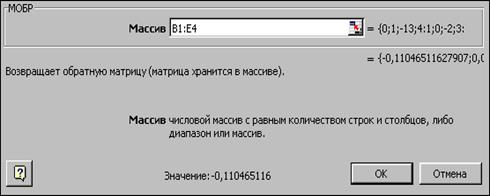
В нашем случае матрица А находится в ячейках B1:Е4, а вектор b в диапазоне G1:G4. Для решения системы методом обратной матрицы необходимо вычислить матрицу, обратную к A. Для этого выделим ячейки для хранения обратной матрицы (это нужно сделать обязательно. ); пусть в нашем случае это будут ячейки B6:E9. Теперь обратимся к мастеру функций, и в категории Математические выберем функцию МОБР,предназначенную для вычисления обратной матрицы (рис. 3.2), щелкнув по кнопке OK, перейдём ко второму шагу мастера функций. В диалоговом окне, появляющемся на втором шаге мастера функций, необходимо заполнить поле ввода Массив(рис. 3.3). Это поле должно содержать диапазон ячеек, в котором хранится исходная матрица — в нашем случае B1:E4. Данные в поле ввода Массив можно ввести, используя клавиатуру или выделив их на рабочем листе, удерживая левую кнопку мыши.
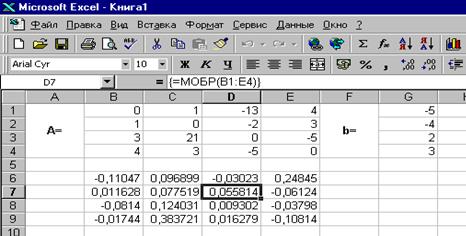
Если поле Массив заполнено, можно нажать кнопку OK. В первой ячейке, выделенного под обратную матрицу диапазона, появится некое число. Для того чтобы получить всю обратную матрицу, необходимо нажать клавишу F2 для перехода в режим редактирования, а затем одновременно клавиши Ctrl+Shift+Enter. В нашем случае рабочая книга MS Excel примет вид изображенный на рис. 3.4.
Теперь необходимо умножить полученную обратную матрицу на вектор b. Выделим ячейки для хранения результирующего вектора, например H6:H9. Обратимся к мастеру функций, и в категории Математические выберем функцию МУМНОЖ,которая предназначена для умножения матриц. Напомним, что умножение матриц происходит по правилу строка на столбец и матрицу А можно умножить на матрицу В только в том случае, если количество столбцов матрицы А равно количеству строк матрицы В. Кроме того, при умножении матриц важен порядок сомножителей, т.е. АВ≠ВА
Перейдём ко второму шагу мастера функций. Появившееся диалоговое окно (рис. 3.5) содержит два поля ввода Массив1 и Массив2. В поле Массив1 необходимо ввести диапазон ячеек, в котором содержится первая из перемножаемых матриц, в нашем случае B6:E9 (обратная матрица), а в поле Массив2 ячейки, содержащие вторую матрицу, в нашем случае G1:G4 (вектор b).
Если поля ввода заполнены, можно нажать кнопку OK. В первой ячейке выделенного диапазона появится соответствующее число результирующего вектора. Для того чтобы получить весь вектор, необходимо нажать клавишу F2, а затем одновременно клавиши Ctrl+Shift+Enter. В нашем случае результаты вычислений (вектор х), находится в ячейках H6:H9.
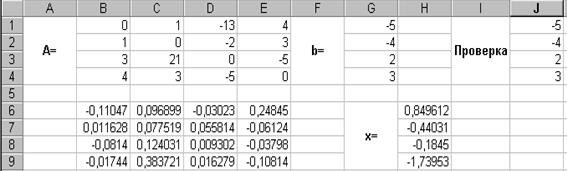
Для того чтобы проверить, правильно ли решена система уравнений, необходимо умножить матрицу A на вектор xиполучить в результате вектор b. Умножение матрицы A на вектор x осуществляется при помощи функции МУМНОЖ(В1:Е4;Н6:Н9), так как было описанной выше.
В результате проведенных вычислений рабочий лист примет вид изображенный на рис. 3.6.
ПРИМЕР 3.2. Решить систему из ПРИМЕРА 3.1 методом Крамера.
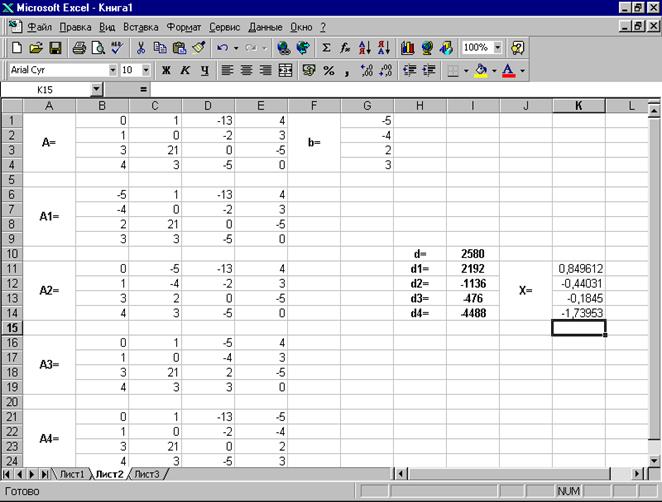
Введём матрицу А и вектор b на рабочий лист. Кроме того, сформируем четыре вспомогательные матрицы, заменяя последовательно столбцы матрицы A на столбец вектора b (рис. 3.7).
Для дальнейшего решения необходимо вычислить определитель матрицы A. Установим курсор в ячейку I10 и обратимся к мастеру функций. В категории Математические выберем функцию МОПРЕД,предназначенную длявычисления определителя матрицы, и перейдём ко второму шагу мастера функций. Диалоговое окно, появляющееся на втором шаге содержит поле ввода Массив.В этом поле указывают диапазон матрицы, определитель которой вычисляют. В нашем случаеэтоячейки B1:E4.
Для вычисления вспомогательных определителей введем формулы:
В результате в ячейке I10 хранится главный определитель, а в ячейках I11:I14 – вспомогательные.
Воспользуемся формулами Крамера и разделим последовательно вспомогательные определители на главный. В ячейку K11 введём формулу =I11/$I$10. Затем скопируем её содержимое в ячейки K12, K13 и K14. Система решена.
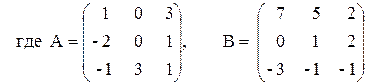
ПРИМЕР 3.3. Вычислить матрицу С по формуле: C=A 2 +2AB, где
Введем исходные данные на рабочий лист (рис. 3.8).
Для умножения матрицы А на матрицу В, выделим диапазон B5:D7ивоспользуемся функцией МУМНОЖ(B1:D3;G1:I3).
Результат вычисления A 2 =A*Aпоместим в ячейкиG5:I7,воспользовавшисьформулой МУМНОЖ(B1:D3;B1:D3).
Умножение (деление) матрицы на число можно выполнить при помощи элементарных операций. В нашем случае необходимо умножить матрицу из диапазона B5:D7начисло 2. Выделим ячейки B9:D11 и введем формулу =2*B5:D7.
Сложение (вычитание) матриц выполняется аналогично. Например, выделим диапазон G9:I11 и введем формул =B9:D11+ G5:I7.
Для получения результата в обоих случаях необходимо нажать комбинацию клавиш Ctrl+Shift+Enter.
Кроме того, в строке формул рабочего листа, изображенного на рис. 3.8, показано как можно вычислить матрицу Содним выражением.
ВАРИАНТЫ З А Д А Н И Й
1. Решить систему уравнений методом Крамера.
2. Решить систему уравнений с помощью обратной матрицы.
3. Выполнить действия над матрицами.
При решении систем обязательно выполнить проверку.
Вариант №1 1) 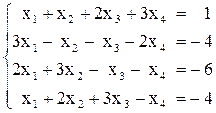
3) 2 (A + B) (2B – A),
Вариант №2 1) 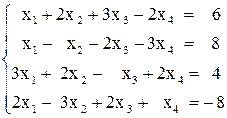
3) 3 A — (A + 2B) B,
Вариант № 3 1) 
3) 2(A–B)(A 2 + B),
Вариант №4 1) 
3) (A 2 – B 2 )(A + B),
Вариант №5 1) 
3) (A–B 2 )(2A+B),
Вариант №6 1) 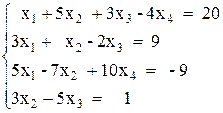
3) (A – B) A + 2B,
Вариант №7 1) 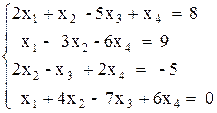
3) 2(A–0,5B)+AB,
Вариант №8 1) 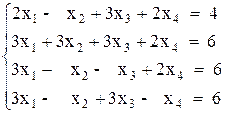
3) (A – B)A + 3B,
Вариант №9 1) 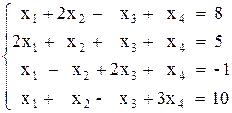
3) 2A – (A 2 + B) B,
Вариант №10 1) 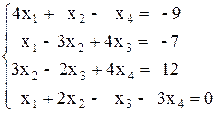
3) 3 (A 2 – B 2 ) –2АB,
Вариант №11 1) 
3) (2A–B)(3А+B)–2АВ,
Вариант №12 1) 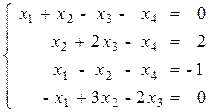
3) А(A 2 –B)-2(B+А)В,
Вариант №13 1) 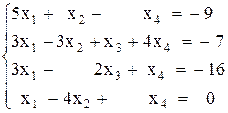
3) (A+B)A–B(2А+3В),
Вариант №14 1) 
3) A(2A+B)–B(А–В),
Вариант №15 1) 
3) 3(A+B)(AВ–2А),
Вариант №16 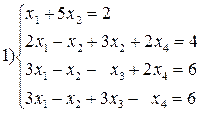
3) 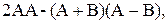
Вариант №17 1) 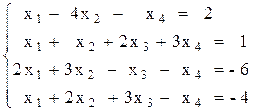
3) 2А + 3B(АB-2А),
Вариант №18 1) 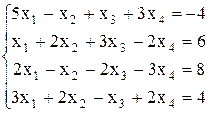
3)
Вариант №191) 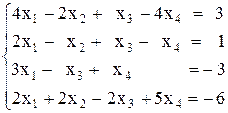
3) 2A — АB(В — А) + В,
Вариант №20 1) 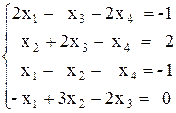
3) A 2 — (A + B)–(А – 3В),
Вариант №21 1) 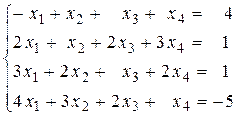
3)
Вариант№22

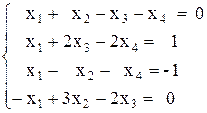
3) А(A — B) + 2В(A + В),
Вариант№24 1) 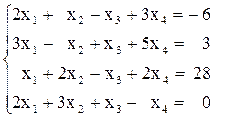
Вариант№25
Вариант №26
Вариант №27
Вариант №28
Вариант№29
Вариант №30
Видео:ЛИНЕЙНЫЕ УРАВНЕНИЯ - Как решать линейные уравнения // Подготовка к ЕГЭ по МатематикеСкачать

Лабораторная работа №6. решение задач линейной алгебры в ms excel
Цель работы: познакомиться с приемами решения задач линейной алгебры.
Типичными задачами линейной алгебры являются задачи, связанные с решением систем линейных уравнений. При этом приходится работать с массивами чисел. Для их обработки в Excel предусмотрен ряд математических функций:
- МОПРЕД(массив) — функция для нахождения определителя квадратной матрицы. Здесь массив — числовой массив с равным количеством строк и столбцов;
- МОБР(массив) — функция для нахождения обратной матрицы. Здесь массив — числовой массив с равным количеством строк и столбцов;
- МУМНОЖ(массив1;массив2) — функция для нахождения произведения массива1на массив2.Результатом является массив с таким же числом строк, как массив1, и с таким же числом столбцов, как массив2. При этом если обозначить буквой С результат произведения двух массивов А и В, то элементы массива С определяются по формуле
, где i — номер строки, а j — номер столбца;
- ТРАНСП(массив) — функция для транспонирования массива ячеек на рабочем листе. Транспонирование массива заключается в том, что первая строка массива становится первым столбцом нового массива, вторая строка массива становится вторым столбцом нового массива и т.д.
Особенностью вычислений, связанных с массивами, является то, что результат вычисления распространяется в виде формулы на целый блок ячеек. Такие формулы называются формулами массива. При вводе формул массива необходимо соблюдать определенную последовательность действий:
Шаг 1. Сначала формула вводится в первую ячейку результирующего массива.
Шаг 2.Выделяется весь блок ячеек результирующего массива.
Шаг 3.Нажимается клавишаклавиатуры.
Шаг 4.Нажимается комбинация клавиш Ctrl+Shift+Enter. При этом формула распознается как формула массива и заключается в фигурные скобки .
При работе с массивами чисел всегда контролируйте размерность результирующего массива!
ЗАДАНИЕ 1. Решение задач линейной алгебры
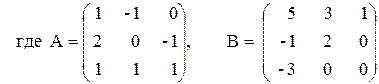
Рассмотрим решение некоторых задач линейной алгебры на простейших примерах. Пусть дана квадратная матрица 3-го порядка 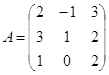
- Найдите матрицу А-1, обратную к данной матрице А.
- Найдите определитель матрицы А.
- Проверьте, что найденная матрица А-1 действительно является обратной для матрицы А.
1. Откройте чистый рабочий лист. Переименуйте его в Обратная матрица.
2. Заполните рабочий лист исходными данными, как показано на рис. 14:
3. Установите курсор в ячейку Е2 и введите формулу =МОБР(А2:С4). После нажатия клавиши Enter в ячейке Е2 появится число 0,4.
4. Для получения обратной матрицы формулу в этом примере необходимо ввести как формулу массива. Для этого выделите диапазон ячеек Е2:G4, соответствующий обратной матрице (размерность матрицы А-1 очевидно будет такая же, как и у матрицы А). Нажмите клавишу , а затем комбинацию клавиш Ctrl+Shift+Enter. В результате ячейки Е2:G4 будут заполнены элементами обратной матрицы.
5. В ячейку А6 введите текст Определитель(A).
6. Установите курсор в ячейку В6 и введите формулу = МОПРЕД(А2:С4). Нажмите клавишу Enter. В ячейке должно получиться значение определителя матрицы А, равное 5. Внимание!В этом случае формулу для расчета определителя не нужно вводить как формулу массива, так как определитель является не массивом, а одним числом.
7. Для проверки правильности нахождения обратной матрицы вспомним, что должно выполняться условие: А А-1=Е, где Е — единичная матрица того же порядка, что и матрица А. Установите курсор в ячейку Е6 и введите текст Произведение матриц.
8. В ячейку Е7 введите формулу = МУМНОЖ(А2:С4; Е2:G4). Нажмите клавишу Enter.
9. Формулу в этом случае также вводим как формулу массива. В результате ячейки Е7:G9 будут заполнены элементами единичной матрицы (по главной диагонали будут записаны 1, остальные элементы будут равны 0). Если числа имеют много десятичных знаков, то выделите ячейки Е7:G9 и уменьшите разрядность либо при помощи команды меню Формат/Ячейки/закладка Число, либо при помощи кнопки Уменьшить разрядность 
ТЕСТОВОЕ ЗАДАНИЕ 1. Решение систем линейных уравнений
Вариант вашего задания задает преподаватель!
Откройте чистый рабочий лист. Переименуйте его в Тест 1.Решите систему линейных уравнений (см. табл. 5) по формулам Крамера.
Формулы Крамера имеют вид:
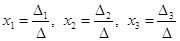
Здесь D- определитель системы, а Di — вспомогательный определитель, который получается из исходного определителя D путем замены i-го столбца на столбец свободных членов уравнений системы.
| № | Решить систему | № | Решить систему |
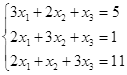 | 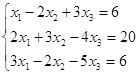 | ||
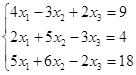 | 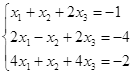 | ||
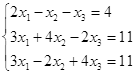 | 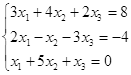 | ||
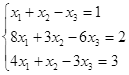 | 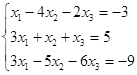 | ||
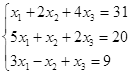 | 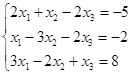 | ||
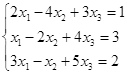 | 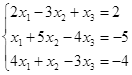 | ||
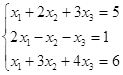 | 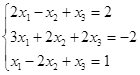 | ||
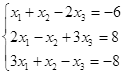 | 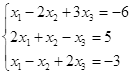 | ||
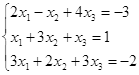 | 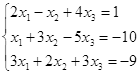 | ||
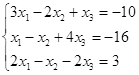 | 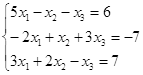 | ||
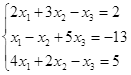 | 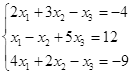 | ||
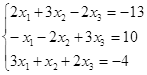 | 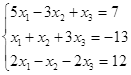 | ||
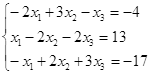 | 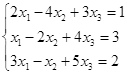 | ||
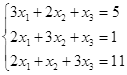 | 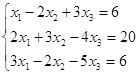 | ||
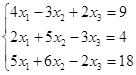 | 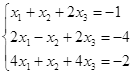 |
ТЕСТОВОЕ ЗАДАНИЕ 2. Решение уравнений, записанных в матричной форме
Вариант вашего задания задает преподаватель!
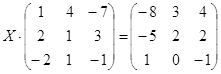
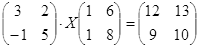
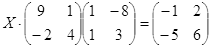
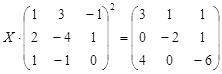
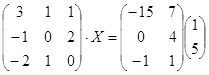
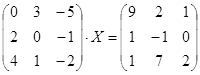
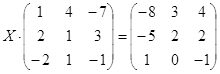
Откройте чистый рабочий лист. Переименуйте его в Тест 2.Решите матричные уравнения, выбрав свой вариант из таблицы 6.
Примечание. Заданное уравнение нужно свести к одному из двух видов:
1) А Х=В, здесь решение находится по формуле Х=А-1 В
2) Х А =В, в этом случае решение находится по формуле Х=В А-1.
Если исходное уравнение имеет вид С Х А =В, то его предварительно приведите к виду: Х А = С-1 В, рассчитайте правую часть системы и затем воспользуйтесь предложенными формулами для нахождения решения системы.
| № | Уравнение | № | Уравнение |
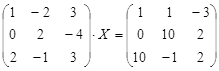 |  | ||
 |  | ||
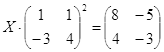 | 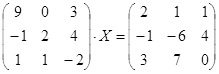 | ||
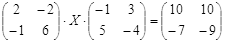 | 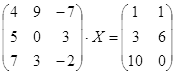 | ||
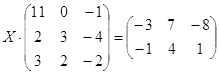 |  | ||
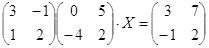 |  | ||
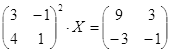 | 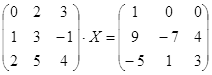 | ||
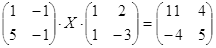 | 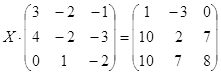 | ||
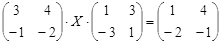 |  | ||
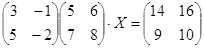 | 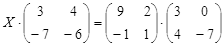 | ||
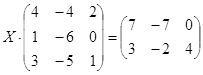 | 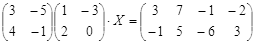 | ||
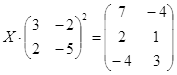 | 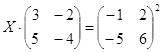 | ||
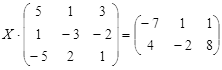 | 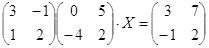 | ||
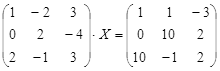 |  | ||
 |  |
Статьи к прочтению:
Курс Excel_Базовый — Урок №8. Абсолютные и относительные ссылки
Похожие статьи:
САМАРСКАЯ ГОСУДАРСТВЕННАЯ АКАДЕМИЯ ПУТЕЙ СООБЩЕНИЯ Кафедра информатики ИНФОРМАТИКА Табличный процессор MS Excel Методические указания к выполнению…
Цель работы: познакомиться с возможностями организации циклических вычислений на примере расчетов сумм и произведений. Обычно при расчетах сумм или…
Видео:Урок 7 ЛИНЕЙНОЕ УРАВНЕНИЕ С ОДНОЙ ПЕРЕМЕННОЙСкачать

Лабораторная_работа «Решение системы линейных уравнений»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Матричные методы решения систем линейных алгебраических уравнений
Цель работы: приобрести навыки решения линейных алгебраических уравнений в среде Excel .
1. Изучить представленный ниже материал, повторить приведенные примеры
В общем виде система линейных алгебраических уравнений записывается следующим образом:
Эту систему можно представить в матричном виде: AX = b , где



Метод обратной матрицы
Систему линейных алгебраических уравнений AX = b умножим слева на матрицу, обратную к матрице А . Система уравнений примет вид:
Вектор неизвестных вычисляется по формуле X=A -1 b .
В этом случае неизвестные x 1 , x 2 ,…, x n вычисляются по формуле:
где – определитель матрицы A ;
I – определитель матрицы, получаемой из матрицы А путем замены i -го столбца вектором b.
Рассмотрим решение системы линейных уравнений методом обратной матрицы и методом Крамера на следующих примерах.
Решить систему линейных уравнений методом обратной матрицы:
Матрица коэффициентов А и вектор свободных коэффициентов b имеют вид:

.
Введем эти данные в рабочий лист Excel (рисунок 12).
Рисунок 12 – Шаг 1 решения системы линейных уравнений
Для решения системы методом обратной матрицы необходимо вычислить матрицу, обратную к A . Для этого определим ячейки для хранения обратной матрицы, пусть это будут ячейки B6:E9.
Обратимся к мастеру функций, и выберем функцию МОБР , щелкнув по кнопке OK, перейдём ко второму шагу мастера функций. В диалоговом окне, появляющемся на следующем шаге мастера функций, необходимо заполнить поле ввода Массив . Это поле должно содержать диапазон ячеек, в котором хранится исходная матрица — в нашем случае B1:E4. Данные в поле ввода Массив можно ввести, используя клавиатуру или выделив их на рабочем листе, удерживая левую кнопку мыши.
Если поле Массив заполнено, нажать кнопку OK. В первой ячейке, выделенного под обратную матрицу диапазона, появится некое число. Для того чтобы получить всю обратную матрицу, необходимо нажать клавишу F2, а затем одновременно клавиши Ctrl+Shift+Enter. Рабочий лист Excel примет вид, изображенный на рисунке 13.
Р
исунок 13 – Шаг 2 решения системы линейных уравнений
Теперь необходимо умножить полученную обратную матрицу на вектор b . Выделим ячейки для хранения результирующего вектора, например H6:H9. Обратимся к мастеру функций, и выберем функцию МУМНОЖ , предназначенную для умножения матриц. На втором шаге мастера функций в диалоговом окне введем в поле Массив1 необходимо ввести диапазон ячеек, в котором содержится первая из перемножаемых матриц, в нашем случае B6:E9 (обратная матрица), а в поле Массив2 ячейки, содержащие вторую матрицу, в нашем случае G1:G4 (вектор b ).
Для того чтобы проверить, правильно ли решена система уравнений, необходимо умножить матрицу A на вектор х и получить в результате вектор b . Умножение матрицы A на вектор x осуществляется при помощи функции = МУМНОЖ (В1:Е4;Н6:Н9), так как было описанной выше.
В
результате проведенных вычислений рабочий лист примет вид изображенный на рисунке 13.
Рисунок 13 – Шаг 3 решения системы линейных уравнений матричным методом
Решим пример методом Крамера.
Введём матрицу А и вектор b на рабочий лист. Сформируем четыре вспомогательные матрицы, заменяя последовательно столбцы матрицы A на столбец вектора b (рисунок 14).
Для дальнейшего решения необходимо вычислить определитель матрицы A. Установим курсор в ячейку I10 и обратимся к мастеру функций. В категории Математические выберем функцию МОПРЕД, предназначенную для вычисления определителя матрицы, и перейдём ко второму шагу мастера функций. Диалоговое окно, появляющееся на втором шаге содержит поле ввода Массив. В этом поле указывают диапазон матрицы, определитель которой вычисляют. В нашем случае это ячейки B1:E4.
Для вычисления вспомогательных определителей введем формулы:
I12= МОПРЕД (B11:E14) ,
I13= МОПРЕД (B16:E19),
I14= МОПРЕД (B21:E24) .
В результате в ячейке I10 хранится главный определитель, а в ячейках I11:I14 — вспомогательные.
Воспользуемся формулами Крамера и разделим последовательно вспомогательные определители на главный. В ячейку K11 введём формулу=I11/$I$10. Затем скопируем её содержимое в ячейки K12, K13 и K14. Система решена.
Рисунок 14 — Решения системы линейных уравнений методом Крамера
2. Решить системы уравнений согласно вариантам с помощью обратной матрицы и методом Крамера.
При решении систем обязательно выполнить проверку.
Вариант 2 Вариант 3 Вариант 4 Вариант 5 Вариант 6 Вариант 7 Вариант 8 Вариант 9 Вариант 10 Вариант 11 Вариант 12 Вариант 13 Вариант 14 Вариант 15 Вариант 16 Вариант 17 Вариант 18 Вариант 19 Вариант 20
Обратите внимание на особенность работы с матричными формулами: необходимо предварительно выделять область, в которой будет храниться результат, а после получения результата преобразовывать его к матричному виду, нажав клавиши F2 и Ctrl+Shift+Enter.
💥 Видео
Линейное уравнение с одной переменной. Практическая часть. 6 класс.Скачать

Алгебра 7 Линейное уравнение с одной переменнойСкачать

Линейное уравнение с одной переменной. Практическая часть. 6 класс.Скачать

Линейное уравнение с одной переменной. Практическая часть. 6 класс.Скачать

Линейное уравнение с двумя переменными. 7 класс.Скачать

Линейное уравнение с одной переменной. 6 класс.Скачать

Решение системы уравнений методом ГауссаСкачать

Алгебра 7 класс (Урок№44 - Решение задач с помощью линейных уравнений.)Скачать

Решение системы линейных уравнений графическим методом. 7 класс.Скачать

Как решать уравнения? уравнение 7 класс. Линейное уравнениеСкачать

Лабораторная работа 2. Решение систем алгебраических уравненийСкачать

Решение системы линейных уравнений графическим методом. Практическая часть. 7 класс.Скачать

Алгебра 7 класс (Урок№43 - Решение линейных уравнений с одним неизвестным.)Скачать

Математика это не ИсламСкачать

Видеоурок. 7 класс. Решение линейных уравнений с одним неизвестнымСкачать

Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Решение системы линейных алгебраических уравнений (СЛАУ) в Excel МАТРИЧНЫМ МЕТОДОМСкачать

Лабораторная работа по Exel “решение уравнения»Скачать

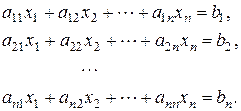
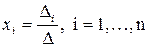

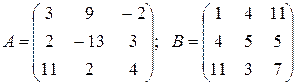

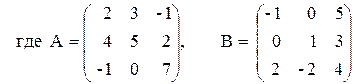
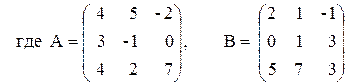
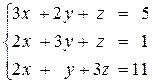

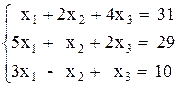
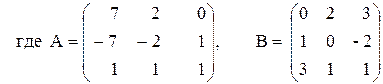
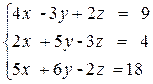
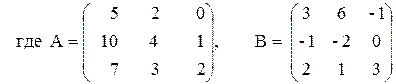
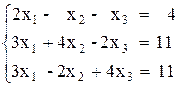

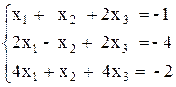
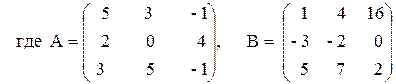

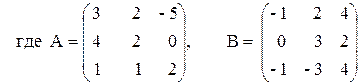
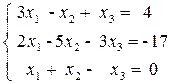
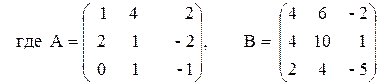

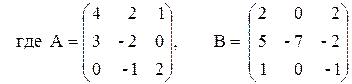


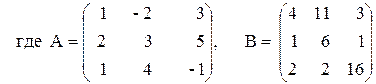

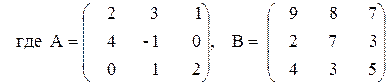
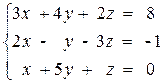


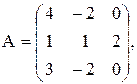

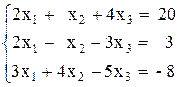
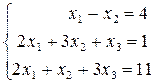

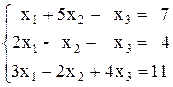
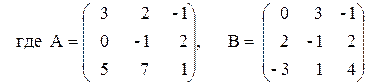

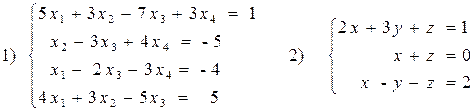
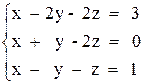
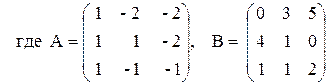
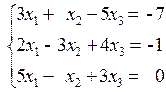
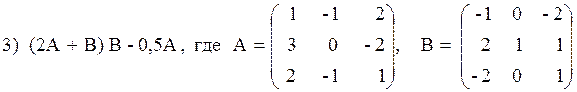
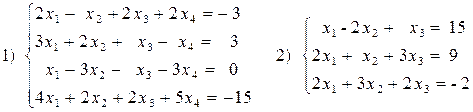

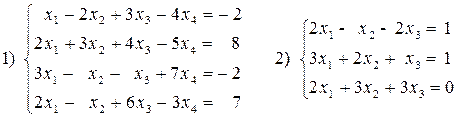
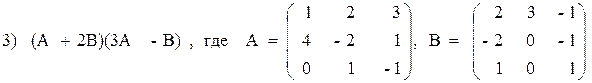

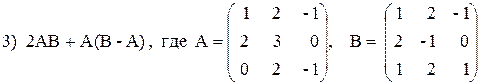
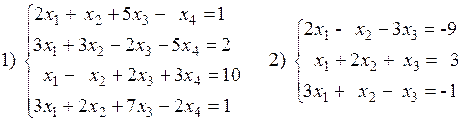
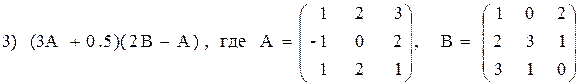

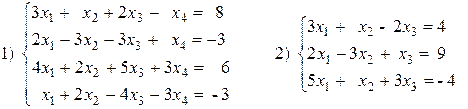
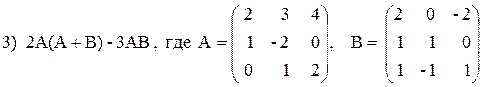
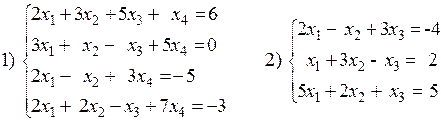
 , где i — номер строки, а j — номер столбца;
, где i — номер строки, а j — номер столбца;