Лабораторная работа изучение уравнения бернулли для идеальной и вязкой жидкости

ЛАБОРАТОРНАЯ РАБОТА № 4

Практическое ознакомление с уравнением Д.Бернулли

1 Цель работы:

На напорном трубопроводе переменного сечения при установившемся движении подтвердить энергетический баланс потока жидкости и представить его графическое доказательство.

2 Общие сведения.

Движение жидкости характеризуется скоростями движения частиц и давлением в отдельных точках потока.

Впервые в 1738 г. Д. Бернулли вывел уравнение для элементарной струйки идеальной жидкости

Уравнение 1 устанавливает связь между скоростью движения, давлением и геометрическим положением частиц жидкости для двух сечений струйки.

Уравнение Бернулли для плавно изменяющегося потока вязкой жидкости имеет вид:

где z – геометрическая высота центра сечения потока, р – давление, ρ – плотность жидкости, V – скорость потока в сечении, α – коэффициент Кориолиса, учитывающий неравномерность распределения скорости по сечению.

Таблица 1 Геометрический и энергетический смысл уравнения Бернулли

Член уравнения Бернулли

Геометрический смысл: При установившемся потоке реальной жидкости сумма четырех высот ( высота положения, пьезометрическая высота, высота скоростного напора и высота потерь напора) есть величина постоянная для любого сечения потока.

Рисунок 1

Энергетический смысл: при установившемся потоке реальной жидкости сумма четырех удельных энергий (энергии положения, энергии давления, кинетической энергии и энергии потерь) остается неизменной для любого сечения потока.

3 Порядок выполнения работы.

Наглядно уравнение Бернулли демонстрируется на установке, представляющего собой участок напорного трубопровода переменного сечения. В центры тяжести выбранных сечений установлены пьезометры и трубки Пито. Трубка Пито — это изогнутая под углом 900 трубка, устанавливаемая отверстием наконечника против течения.

На рисунке приведена схема трубопровода с трубками Пито. В каждой паре трубки слева (пьезометрические) показывают пьезометрическую высоту , она уменьшается с переходом воды из широкого сечения в узкое и снова увеличивается при переходе из узкого сечения в широкое. Трубки справа показывают , где u – скорость набегающей струйки. С уменьшением давления скоростной напор возрастает. Полный напор, или удельная энергия струйки неравномерно уменьшается по течению, так как часть его затрачивается на преодоление сопротивлений. Движение воды по трубопроводу создается за счет работы центробежного насоса 2, осуществляющего циркуляцию воды в системе. Забор воды производится насосом из бака 1, которая возвращается в тот же бак. Через напорный трубопровод 5 пропускается расход воды Q регулируемый с помощью вентиля 3. По показаниям пьезометров записывается пьезометрический напор (удельная потенциальная энергия) и по показаниям динамических трубок – полный напор (полная удельная энергия струйки) .

Скоростной напор определяется как разность между показаниями динамических и пьезометрических трубок. По скоростному напору находится величина скорости на оси струйки потока, где расположены открытые концы динамических трубок.

Для определения удельной энергии всего потока надо определить скоростной напор , вычисленный по средней скорости с учетом α (при турбулентном режиме движения α принимается равным 1,05 — 1,1; при ламинарном режиме α = 2. Средние скорости V в сечениях трубы определяется по расходу Q, .

Расход определяется как , где W — объем жидкости, прошедший через водомер 6; τ — время прохождения этого объема, S_i –площадь трубы в данном сечении трубопровода. По полученным значениям на миллиметровке строится пьезометрическая линия и по значениям – линии полной удельной энергии потока.

Построение линии дает наглядное представление о перераспределении энергии, в соответствии с измерениями живого сечения вдоль потока, согласно уравнению Бернулли.

Рисунок 2. Схема размещения пьезометра и трубки Пито	Рисунок 3 . Напорная и пьезометрическая линии по сечениям канала

4 Обработка результатов испытаний.

Все полученные данные сводятся в таблицу 2

Таблица 2 . Результаты замеров и расчетов

5. Содержание отчета

1. Краткие теоретические данные

2. Схему установки

3. Описание произведенного опыта

4. Обработку результатов опыта в виде таблицы и произведенных расчетов

5. Графики полного напора и пьезометрических высот

6. Основные выводы по работе

6. Контрольные вопросы.

1. Что называют полной удельной энергией потока в произвольном сечении? 2. Запишите уравнение Бернулли для элементарной струйки идеальной жидкости?

4. Запишите уравнение Бернулли для потока реальной жидкости?

5. В чем состоит геометрический смысл уравнения Бернулли?

6. В чем состоит энергетический смысл уравнения Бернулли?

7. Почему напорная линия всегда нисходящая?

8. Почему пьезометрическая линия бывает нисходящей и восходящей?

9. На каком расстоянии друг от друга располагаются напорная и пьезометрическая линии?

10. Могут ли напорная и пьезометрическая линии пересекаться?

11. Как изменяется площадь живого сечения вдоль потока, если расстояние между напорной и пьезометрическими линиями вдоль потока при протекании по трубопроводу жидкости с постоянным расходом увеличится?

Видео:Урок 133. Закон Бернулли. Уравнение БернуллиСкачать

Дистанционная лабораторная работа 5 по иллюстрации уравнения Бернулли

Цель работы. Опытное подтверждение уравнения Д. Бернулли, т. е. понижения механической энергии по течению и перехода потенциальной энергии в кинетическую и обратно (связи давления со скоростью).

Задание. На основе замеров при просмотре фильма и анализе фотографии течения жидкости в канале переменного сечения в устройстве № 4 построить линии энергий для потока и проверить их соответствие уравнению Бернулли.

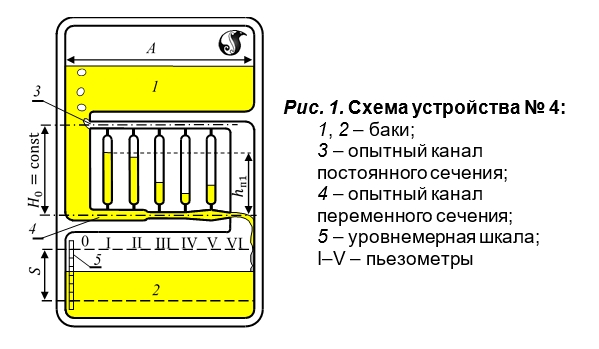
Описание устройства № 4. Устройство № 4 содержит баки 1 и 2, сообщаемые через опытные каналы постоянного 3 и переменного 4 сечений (рис. 1). Каналы соединены между собой равномерно расположенными пьезометрами I–V, служащими для измерения пьезометрических напоров в характерных сечениях. Устройство заполнено подкрашенной водой.

В одном из баков предусмотрена шкала 5 для измерения уровня воды. При перевертывании устройства, благодаря постоянству напора истечения Н о во времени, обеспечивается установившееся движение воды в нижнем канале. Другой канал в это время пропускает воздух, вытесняемый жидкостью из нижнего бака в верхний.

Порядок выполнения работы.

1. Зарисовать схему устройства № 4 и составить таблицу следующего вида.

2. Посмотреть фильм с демонстрацией течения воды через канал переменного сечения в устройстве № 4 и секундомером замерить время t полного опорожнения верхнего бака.

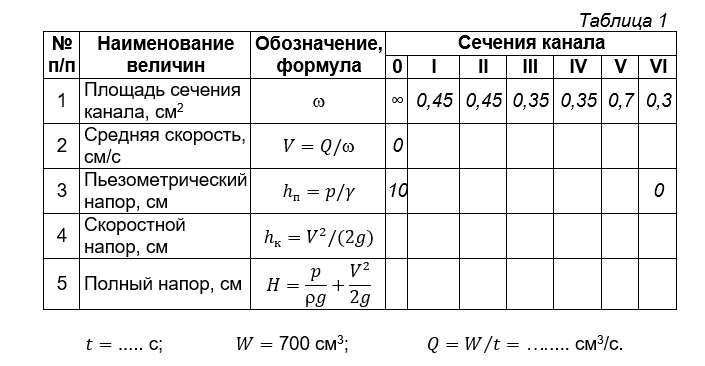
3. Под таблицей записать значение времени t t опорожнения бака, объем бака принять равным W=700 см 3 и определить расход Q=W/t Q = W t .

4. В строке (стр.) 2 рассчитать среднюю скорость течения жидкости в каждом сечении канала: V=Q / w ω Скорость в нулевом сечении (перед входом в канал) принять равной нулю.

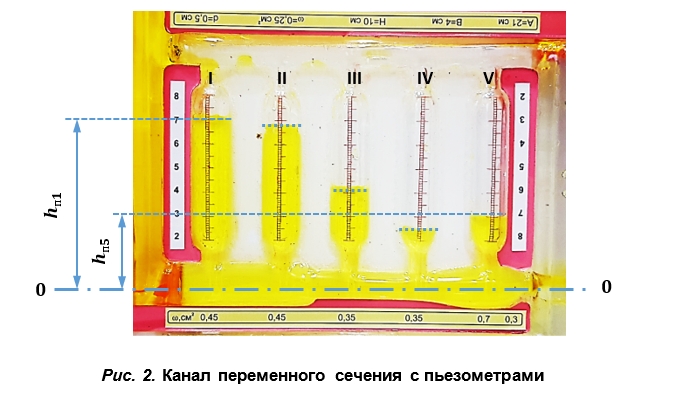
5. На фотографии канала с пьезометрами (рис. 2) снять показания пьезометров h_П1 . . . . h_П5 и записать их в стр. 3. В сечении VI пьезометрический напор равен 0.

6. В стр. 4 определить скоростной напор h_к в сечениях канала. Принять g = 981 см/с 2 .

7. В стр. 5 определить полный напор H H (полную удельную энергию) в каждом сечении. Так как опытный канал горизонтальный и плоскость сравнения 0–0 проведена через его ось, то геометрический напор z₁= z₂= 0 .

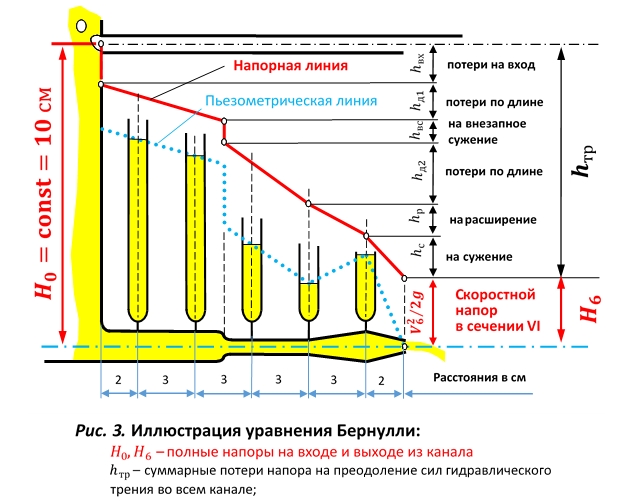
8. Вычертить в масштабе канал с осями пьезометров (рис. 3). Отложить от оси канала пьезометрические напоры h_П h _п на осях пьезометров, наметить уровни жидкости и соединить их между собой и центром выходного сечения VI , как показано на рис. 3. Получится пьезометрическая линия, показывающая изменение потенциальной энергии (давления) вдоль потока. Для получения напорной линии (линии полной механической энергии) нужно отложить от оси канала полные напоры Н и соединить полученные точки, как показано на рис. 3.

9. Проанализировать изменения полной механической H , потенциальной 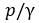и кинетической V 2 /(2g) V 2 /(2 g ) энергий жидкости вдоль потока и проверить их соответствие нижеприведенным правилам построения линий энергий, вытекающим из уравнения Бернулли.

А. Напорная линия (полный напор 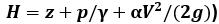постоянно понижается по течению (если на рассматриваемом участке нет насоса) ввиду необратимого преобразования механической энергии в тепловую при преодолении потоком сил гидравлического трения. Причем уклон линии (потери напора h тр ) тем больше, чем меньше сечение участка потока (см. рис. 3).

Б. Пьезометрическая линия отражает изменение потенциальной энергии (z + 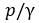) , и, в отличие от напорной, может не только понижаться, но и повышаться по течению. Это происходит при расширении потока (см. рис. 2, 3) за счет повышения давления p ввиду уменьшения скорости V . Пьезометрическая линия проходит через центр тяжести выходного сечения канала (трубопровода) при истечении жидкости в атмосферу и ниже оси канала, если давление в нем меньше атмосферного.

В. Расстояние между пьезометрической и напорной линиями численно равно кинетической энергии 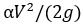α V 2 /( 2 g ) и поэтому обратно пропорционально диаметру трубы. Для участков потоков постоянного сечения средние скорости одинаковы по пути, поэтому такие линии, как правило, параллельны между собой (рис. 3). Эти линии для потоков в конфузорах (конических сходящихся патрубках) расходятся, а в диффузорах (конических расходящихся патрубках) – сходятся. В баках и водоёмах, где жидкость не движется (V=0) ( V =0) , напорная и пьезометрическая линии энергий совпадают со свободной поверхностью, если она находится под атмосферным давлением.

10. Записать выводы , где указать какие знания и навыки получены при выполнении данной работы и в каких сферах инженерной деятельности они могут быть применены.

Видео:Закон БернуллиСкачать

Лабораторная работа изучение уравнения бернулли для идеальной и вязкой жидкости

Лабораторная работа № 3 — Экспериментальная проверка уравнения Д.Бернулли

Цель работы : По результатам экспериментальных данных и расчетов построить диаграмму уравнения Д.Бернулли

1 Основные теоретические положения

Уравнение Д.Бернулли для реального потока жидкости для двух произвольно взятых сечений имеет следующий вид:

, (9)

где: z ₁ , z ₂ – нивелирная высота соответственно для первого и второго сечений, м;

– пьезометрическая высота соответственно для первого и второго сечений, м;

– коэффициент кинетической энергии потока (или коэффициент Кориолиса), учитывающий неравномерность распределения скоростей по сечению потока (величина безразмерная);

– скоростная высота или скоростной напор, м;

– сумма всех гидравлических потерь на участке между первым и вторым сечение, м.

Итак, с геометрической точки зрения уравнение Д.Бернулли показывает, что сумма трех высот – геометрической, пьезометрической и скоростной с учетом всех гидравлических потерь – есть величина, постоянная вдоль струйки.

С энергетической точки зрения члены уравнения Д.Бернулли имеют следующий смысл:

z – удельная энергия положения; -.

z + p / y — удельная потенциальная энергия жидкости;

v /2 g кудельная кинетическая энергия.,

Таким образом, – уравнение Д.Бернулли является примером закона сохранения энергии М.В.Ломоносова в применении к жидкости.

2 Описание экспериментальной установки

Экспериментальная установка показана на рисунке 2.

Экспериментальная установка состоит из труоы 1 переменного диаметра (а в шести сечениях которой установлены пьезометры 2. Жидкость подается в напорный бак 3, через трубу 4 и краном 5 регулируется количество поступающей жидкости. В баке^З напор (Н) поддерживается постоянным. Жидкость выливается в мерный бак 6. Краном 7 изменяется расход жидкости проходящей по, трубе 1, а следовательно скорость жидкости, протекающей по трубе 1.

3 Методика проведения эксперимента

Методика проведения эксперимента заключается в следующем. Открыв кран 5 через трубу 4, наполняем, напорный бак 3 до уровня Н. Поддерживая этот уровень • постоянным, краном 7 устанавливаем некоторый расход жидкости и с помощью мерного бака 6 и секундомера определяем время ( t ) наполнения указанного объема — жидкости ( W ). Снимаем показания
пьезометров 2 и заносим их в трубе 1.

4 Регистрация опытных данных:

4.1 Объем воды, поступившей в мерный бак 6 W (см 3 )

4.2 Время наполнения объема t (с)

Тогда расход потока Q = ( c м 3 /с).

🎥 Видео

Уравнение Бернулли гидравликаСкачать

Физика. 10 класс. Течение вязкой жидкости. Формула Стокса. Обтекание тел. Лабораторная работа № 5Скачать

Вязкость. Ламинарное и турбулентное течения жидкостей. 10 класс.Скачать

Закон БернуллиСкачать

Уравнение Бернулли для потока жидкостиСкачать

Галилео. Эксперимент. Закон БернуллиСкачать

ЛР3 Уравнение БернуллиСкачать

Уравнение Бернулли. Практическая часть. 10 класс.Скачать

Гидродинамика. Вывод уравнения БернуллиСкачать

Уравнение Бернулли и его приложения | Гидродинамика, ГидравликаСкачать

14. Движение идеальной жидкостиСкачать

Урок 134. Применения уравнения Бернулли (ч.1)Скачать

Уравнение БернуллиСкачать

Якута А. А. - Механика - Гидростатика. Уравнение Бернулли. Формула ПуайзеляСкачать

Экспериментальное исследование уравнения БернуллиСкачать

Лабораторная работа №1Скачать

Работа 4. Экспериментальная демонстрация уравнения БернуллиСкачать

Дистанционная работа 5 - иллюстрация уравнения БернуллиСкачать