| Название: Итерационные методы решения нелинейных уравнений Раздел: Рефераты по информатике, программированию Тип: лабораторная работа Добавлен 09:43:21 25 июня 2008 Похожие работы Просмотров: 2747 Комментариев: 21 Оценило: 3 человек Средний балл: 5 Оценка: неизвестно Скачать | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
Рис.1
Аналитический метод. Функция 




2. Метод простых итераций. Для построения рабочей формулы перепишем уравнение (1) в виде: 

Если условие выполняется, то итерационный процесс строится по формуле
Заметим, что в точке 


Построим функцию 












Итерационный процесс (3) можно начать, задав произвольное начальное приближение 




Метод Ньютона. В качестве начального приближения 

Заметим, что в точке 




Условия выхода итерационного процесса (5) аналогичны условиям метода простых итераций.
Модифицированный метод Ньютона. Начальное приближение 



Условия выхода итерационного процесса (6) аналогичны условиям метода простых итераций.
Замечание: для того, чтобы сделать вывод о скорости сходимости методов, необходимо в каждом методе выбирать одинаковое начальное приближение.
3. Блок-схема метода простых итераций, метода Ньютона и модифицированного метода Ньютона приведена на рисунке 3.
 |
Ниже в качестве примера приведены программы на языках программирования Паскаль и С, реализующие итерационный процесс метода простых итераций.
ПРИМЕР ПРОГРАММЫ НА ЯЗЫКЕ ПАСКАЛЬ
printf(“%d %.4f %.4f %.4f %.4fn”,n++,x,y,fabs(y-x),
Решение: в результате решения нелинейного уравнения (1) на указанном отрезке тремя методами при начальном приближении 





4. Содержание отчета.
Отчет о проделанной работе должен содержать: номер и название лабораторной работы; цель работы; содержание работы; задание на работу; теоретическую часть работы (вывод итерационных формул); листинг(и) программ(ы); таблицы результатов (в случае, если число итераций в таблице достаточно большое, в отчет занести две первых и две последних итерации); выводы о проделанной работе.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Определить количество корней исходного нелинейного уравнения графическим методом и построить график (пример приведен на рисунке 2).
2. Доказать аналитическим методом единственность корня исходного нелинейного уравнения на указанном отрезке.
3. Построить итерационные формулы, реализующие процесс поиска корня на отрезке методом простых итераций, методом Ньютона и модифицированным методом Ньютона.
4. Составить программу(ы) на любом языке программирования, реализующую(ие) построенные итерационные процессы, используя алгоритм методов, приведенный на рисунке. Печать результатов должен осуществляться на каждом шаге итераций в виде следующей таблицы:
Видео:Метод итерацийСкачать

Метод итераций решения системы уравнений. Пример решения
Решение получаем с помощью калькулятора Решение СЛАУ методом итераций .
Видео:Лабораторная работа №4 Изучение явления электромагнитной индукцииСкачать

Достаточное условие сходимости метода простых итераций
Прежде чем применять метод итераций, необходимо переставить строки исходной системы таким образом, чтобы на диагонали стояли наибольшие по модулю коэффициенты матрицы. Если при этом условие все таки не выполняется, то иногда удается обеспечить сходимость метода с помощью следующего метода.
Пусть дана система Ax = b. Преобразуем ее к виду: x= Qx + c
где Q = E — D•A, c = D•b
Здесь D — некоторая матрица. Нам необходимо подобрать такую матрицу D, чтобы выполнялось условие |Q| 0 =β, тогда:
x 1 =b — a x 0
x 2 =b — a x 1
.
x k+1 =b — a x k
Для нашей задачи достаточное условие сходимости выполняется.
| 10 | 2 | -1 |
| -2 | -6 | -1 |
| 1 | -3 | 12 |
Приведем к виду:
x1=0.5-(0.2x2-0.1x3)
x2=-4.07-(0.33x1+0.17x3)
x3=3-(0.0833x1-0.25x2)
Покажем вычисления на примере нескольких итераций.
N=1
x1=0.5 — 0 • 0.2 — 0 • (-0.1)=0.5
x2=-4.07 — 0 • 0.33 — 0 • 0.17=-4.07
x3=3 — 0 • 0.0833 — 0 • (-0.25)=3
N=2
x1=0.5 — (-4.07) • 0.2 — 3 • (-0.1)=1.61
x2=-4.07 — 0.5 • 0.33 — 3 • 0.17=-4.74
x3=3 — 0.5 • 0.0833 — (-4.07) • (-0.25)=1.94
N=3
x1=0.5 — (-4.74) • 0.2 — 1.94 • (-0.1)=1.64
x2=-4.07 — 1.61 • 0.33 — 1.94 • 0.17=-4.93
x3=3 — 1.61 • 0.0833 — (-4.74) • (-0.25)=1.68
Остальные расчеты сведем в таблицу.
| N | x1 | x2 | x3 | e1 | e2 | e3 |
| 0 | 0 | 0 | 0 | |||
| 1 | 0.5 | -4.07 | 3 | 0.5 | 4.07 | 3 |
| 2 | 1.61 | -4.74 | 1.94 | 1.11 | 0.67 | -1.06 |
| 3 | 1.64 | -4.93 | 1.68 | 0.0274 | 0.19 | -0.26 |
| 4 | 1.65 | -4.9 | 1.63 | 0.013 | -0.0341 | -0.051 |
| 5 | 1.64 | -4.89 | 1.64 | -0.0119 | -0.00416 | 0.00744 |
| 6 | 1.64 | -4.89 | 1.64 | -8.8E-5 | -0.00273 | 0.00203 |
| 7 | 1.64 | -4.89 | 1.64 | -0.000343 | 0.00031 | 0.000691 |
Ответ: x1=1.64, x2=-4.89, x3=1.64
Пример №2 . Решить систему уравнений Ax = b с точностью 0.05 методами: 1) простой итерации; 2) Зейделя. Указание. Для обеспечения выполнения достаточного условия сходимости воспользоваться перестановкой строк в исходной системе уравнений.
Видео:Лабораторная работа №4 по физике для 9 класса "Изучения явления электромагнитной индукции"Скачать

Лабораторная работа №4. Решение нелинейных уравнений
Решение нелинейных уравнений
Цель работы.Изучение численных методов решения нелинейных уравнений.
Задание.Решить нелинейное уравнение указанными в табл.7 методами, предварительно определив интервал [a,b], на котором существует решение уравнения. Сделать проверку решения.
Варианты заданий.Варианты уравнений и методов их решения приведены в табл.7.
| Вар. | Уравнение | Методы решения |
| x=exp(-x) | перебора и половинного деления | |
| x=cos(x) | перебора и хорд | |
| х=x2-1 | перебора и касательных | |
| x=2exp(-x) | перебора и хорд-касательных | |
| x=exp(-3x) | перебора и половинного деления | |
| x=3cos(x) | перебора и хорд | |
| x=exp(-3×2) | перебора и касательных |
Продолжение таблицы 7
| Вар. | Уравнение | Методы решения |
| x=tg(x) | перебора и хорд-касательных | |
| x=cos(2x) | перебора и половинного деления | |
| x=tg(2x)-1 | перебора и хорд | |
| x=exp(-3x)+1 | перебора и касательных | |
| x=exp(-x2) | перебора и хорд-касательных | |
| x= ln(x)+2 | перебора и половинного деления | |
| x=exp(-3x) | перебора и хорд | |
| x2=exp(-x2) | перебора и касательных | |
| x=2exp(-3x)+1 | перебора и хорд-касательных | |
| x=exp(-x2)+2 | перебора и половинного деления | |
| x= ln(x)+3 | перебора и хорд | |
| x=3exp(-3x) | перебора и касательных | |
| x2=exp(-x2)-1 | перебора и хорд-касательных | |
| x=exp(-3×2) | перебора и половинного деления | |
| x=tg(x) | перебора и хорд | |
| x=cos(2x) | перебора и касательных | |
| x=tg(2x)-1 | перебора и хорд-касательных | |
| x=exp(-3x)+1 | перебора и половинного деления |
Математическое описание.Уравнение типа F(x)=0 или x=f(x) называется нелинейным. Решить уравнение это значит найти такое x, при котором уравнение превращается в тождество. В общем случае уравнение может иметь 0; 1; 2;... корней. Рассмотренные ниже численные методы решения нелинейных уравнений позволяют находить один корень на заданном интервале [a,b]. При этом на интервале должен существовать только один корень. Рассмотрим несколько методов решения нелинейных уравнений.
1. Метод перебора. При решении нелинейного уравнения методом перебора задаются начальное значение аргумента x=a и шаг h, который при этом определяет и точность нахождения корней нелинейного уравнения. Пока выполняется условие F(x)*F(x+h)>0 аргумент x увеличиваем на шаг h (x=x+h) . Если произведение F(x)*F(x+h) становится отрицательным, то на интервале [x,x+h] существует решение уравнения. Структограмма метода приведена на рис.3.
| Пока F(x)*F(x+h)>0 | |
| x=x+h | Рис.3 |
2. Метод половинного деления. При решении нелинейного уравнения методом половинного деления задаются интервал [a,b], на котором существует только одно решение, и желаемая точность e. Затем определяется середина интервала с=(а+в)/2 и проверяется условие F(a)F(c) e. Структограмма решения нелинейных уравнений методом половинного деления приведена на рис.4.
| Пока b-a>e | ||||||
| c=(a+b)/2 | ||||||
| F(a)F(c) e | ||||||
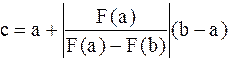 | ||||||
F(a)F(c) e. Для определения точки пересечения (i+1) касательной с осью абсцисс воспользуемся следующей формулой 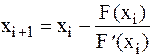 (получите формулу самостоятельно). Условие сходимости метода касательных F(xo)* (получите формулу самостоятельно). Условие сходимости метода касательных F(xo)* 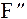 (xo)>0. . Структограмма решения нелинейных уравнений методом касательных показана на рис.6. (xo)>0. . Структограмма решения нелинейных уравнений методом касательных показана на рис.6.
5. Метод хорд-касательных. Если в методе касательных производную функции F'(xi) заменить отношением конечных приращений, то получаем расчетную формулу для метода хорд-касательных 6. Метод итераций. При решении нелинейного уравнения методом итераций воспользуемся записью уравнения в виде x=f(x). Задаются начальное значение аргумента xo и точность e. Первое приближение решения x1 находим из выражения x1=f(x0), второе — x2=f(x1) и т.д. В общем случае i+1 приближение найдем по формуле xi+1 =f(xi). Указанную процедуру повторяем пока f(xi)-xi >e. Условие сходимости метода итераций
Содержание отчета: 1. Название, цель работы и задание. 3. Математическое описание, алгоритм (структограмма) и текст программы. 5. Результаты расчета, проверка и выводы по работе . 💥 ВидеоРешение нелинейного уравнения методом простых итераций (программа)Скачать  Информатика 2. S01.E10. Лабораторная работа №4. Пример (Pascal, excel, word)Скачать  Лабораторная работа № 4 по физике для 8 класса "Сборка электрической цепи и измерение силы тока "Скачать  1 3 Решение нелинейных уравнений методом простых итерацийСкачать  Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать  10 Численные методы решения нелинейных уравненийСкачать  Лабораторная работа по Exel “решение уравнения»Скачать  Решение системы линейных уравнений методом итерацийСкачать  Метод простых итераций - PascalСкачать  Алгоритмы С#. Метод простых итерацийСкачать  7 класс. Лабораторная работа №4. Изучение упругих деформаций.Скачать  Решение систем линейных уравнений методом простой итерации в ExcelСкачать  Численное решение уравнений, урок 4/5. Метод касательных (Ньютона)Скачать  Удалили с экзамена ОГЭ Устное Собеседование shorts #shortsСкачать  Информатика 2. S01.E09. Лабораторная работа №3. Пример (Pascal, excel, word)Скачать  |


 и
и  . Сделать вывод о скорости сходимости всех трех методов.
. Сделать вывод о скорости сходимости всех трех методов. и снова решить задачу. Сделать вывод о точности полученных результатов.
и снова решить задачу. Сделать вывод о точности полученных результатов. (1)
(1) .
. на Рис.1 видно, что функция
на Рис.1 видно, что функция  в одной точке, являющейся приближенным значением корня нелинейного уравнения (1). Но так как данная функция имеет сложный аналитический вид, то преобразуем уравнение (1) к виду
в одной точке, являющейся приближенным значением корня нелинейного уравнения (1). Но так как данная функция имеет сложный аналитический вид, то преобразуем уравнение (1) к виду  и построим два графика
и построим два графика  и
и  , имеющих более простой аналитический вид (Рис.2). Абсцисса точки пересечения графиков является приближенным значением корня. Заметим, что графический метод показывает количество корней исходного уравнения, но не доказывает единственность корня на отрезке.
, имеющих более простой аналитический вид (Рис.2). Абсцисса точки пересечения графиков является приближенным значением корня. Заметим, что графический метод показывает количество корней исходного уравнения, но не доказывает единственность корня на отрезке.
 . Порядок выполнения вычислений в данном методе аналогичен рассмотренному ранее.
. Порядок выполнения вычислений в данном методе аналогичен рассмотренному ранее.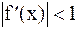 . Структограмма метода итераций показана на рис.7.
. Структограмма метода итераций показана на рис.7.