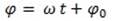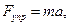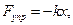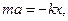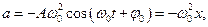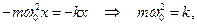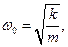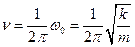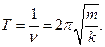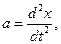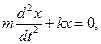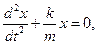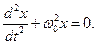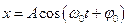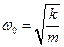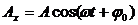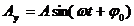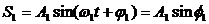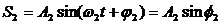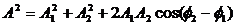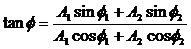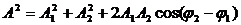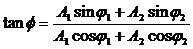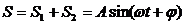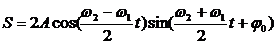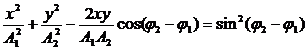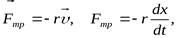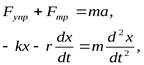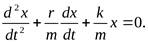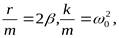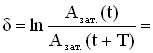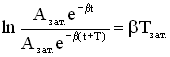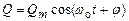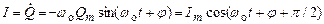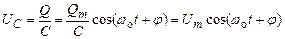Колебания, при которых изменения физических величин происходят по закону косинуса или синуса (гармоническому закону), называются гармоническими колебаниями.
Это простейший вид периодических колебаний. Конкретный вид функции (синус или косинус) зависит от способа выведения системы из положения равновесия. Если выведение происходит толчком (сообщается кинетическая энергия), то при t = 0 смещение х = 0, следовательно, удобнее пользоваться функцией sin, положив
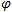
Выражение, стоящее под знаком cos или sin, называется фазой колебания:
Фаза колебания измеряется в радианах и определяет значение смещения (колеблющейся величины) в данный момент времени. Амплитуда колебания зависит только от начального отклонения (начальной энергии, сообщенной колебательной системе).
Упругие и квазиупругие силы.
Систему, состоящую из материальной точки массы m и абсолютно упругой пружины с коэффициентом жесткости k, в которой возможны свободные колебания, называют пружинным маятником.
Запишем второй закон ньютона для рис. Б
Если сила не является по своей природе упругой, но подчиняется закону f = —kх, то она называется квазиупругой силой.
Получим уравнение пружинного маятника. Учтем в записи второго закона ньютона, что
— дифференциальное уравнение точки, совершающей колебательное движение (дифференциальное уравнение пружинного маятника).
Решение дифференциального уравнения:
— уравнение колеблющейся точки (уравнение колеблющейся пружины).
— собственная частота колебаний.
Собственные колебания (свободные колебания), колебания, которые совершаются за счет энергии, сообщенной системе в начале колебательного движения (например, в механической системе через начальное смещение тела или придание ему начальной скорости, а в электрической системе — колебательном контуре — через создание начального заряда на обкладках конденсатора). Амплитуда собственных колебаний в отличие от вынужденных колебаний определяется только этой энергией, а их частота — свойствами самой системы. Вследствие рассеяния энергии собственные колебания всегда являются затухающими колебаниями. Пример собственные колебания — звучание колокола, гонга, струны рояля и т.п.
Сложение гармонических колебаний.
Если колебательная система одновременно участвует в двух (или более) независимых колебательных движениях, возникает задача — найти результирующее колебание. В случае однонаправленных колебаний под этим понимается нахождение уравнения результирующего колебания; в случае взаимно перпендикулярных колебаний — нахождение траектории результирующего колебания.
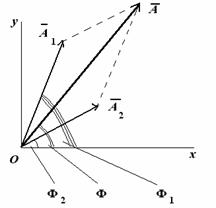
Метод векторных диаграмм
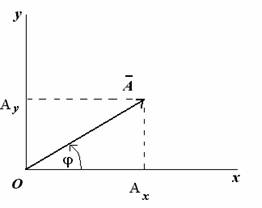
Рассмотрим вращающийся против часовой стрелки с постоянной угловой скоростью вектор а. Очевидно, что угол = t + где — начальный угол.
Проекции вектора а на оси координат запишутся:
Видно, что проекции вращающегося вектора на оси координат по форме совпадают с уравнением гармонических колебаний, если угловой скорости вектора сопоставить угловую частоту колебаний, а начальному углу — начальную фазу.
Проводя аналогию дальше, можно сказать, что результат сложения двух однонаправленных колебаний можно получить следующим путем: необходимо сложить два вектора, а проекции суммарного вектора на оси координат будут являться уравнениями результирующего колебания. Рассмотрим этот метод на примере сложения двух колебаний с произвольными частотами. Пусть наше тело участвует в двух совпадающих по направлению колебаниях:
Сопоставим этим колебаниям два вектора а1 и а2, вращающихся с соответствующими угловыми скоростями.
Сопоставляем колебаниям проекции векторов на ось y. Задача сложения колебаний сводится к нахождению проекции вектора а на ось y (амплитуда результирующего колебания) и угла (фаза результирующего колебания).
Из очевидных геометрических соображений находим:
Отметим, что в общем случае сложения колебаний с разными частотами амплитуда результирующего колебания будет зависеть от времени. Если же частоты одинаковы, то 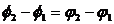
Рассмотрим сложение двух однонаправленных колебаний с неравными, но близкими частотами, то есть 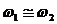
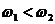
Получим уравнение суммарного колебания:
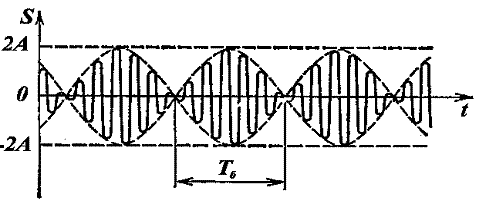
Полученное результирующее колебание не является гармоническим (сравни с уравнением (1)); такого вида колебания носят название биений, название понятно, если посмотреть на график колебаний.
посмотреть на осциллографе
Величина, стоящая перед синусом, меняется со временем относительно медленно, так как разность частот мала. Эту величину условно называют амплитудой биений, а разность складываемых частот 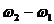
При сложении взаимно перпендикулярных колебаний необходимо найти уравнение траектории тела, то есть из уравнений колебаний типа x = x(t), y = y(t) исключить t и получить зависимость типа y(x).
Например, сложим два колебания с одинаковыми частотами:
Исключив время, получим:
В общем случае это — уравнение эллипса. При a1=a2 — окружность, при 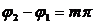
Вид траектории при сложении взаимно перпендикулярных колебаний зависит от соотношения амплитуд, частот и начальных фаз складываемых колебаний. Получающиеся кривые носят название фигур лиссажу.
1. Собственные затухающие механические колебания. Величины, характеризующие быстроту затухания колебаний: коэффициент затухания, логарифмический декремент затухания, добротность, их физический смысл. Апериодический процесс.
Во всякой реальной системе, совершающей механические колебания, всегда действуют те или иные силы сопротивления (трение в точке подвеса, сопротивление окружающей среды и т.п.), на преодоление которых система затрачивает энергию, вследствие чего реальные свободные механические колебания всегда являются затухающими.
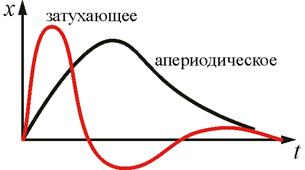
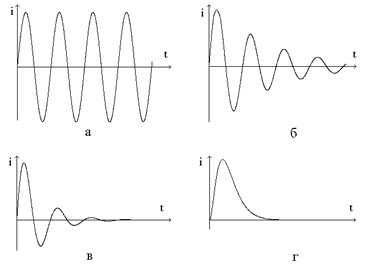
Затухающие колебания- это колебания, амплитуда которых убывает со временем.
Найдем закон изменения амплитуды.
Для пружинного маятника массой m, совершающего малые колебания под действием упругой силы 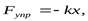
Где r- коэффициент сопротивления среды; знак минус означает, что 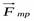
Согласно ii закону ньютона уравнение движения маятника имеет вид:
Обозначим:
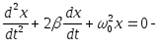
Решением этого уравнения является выражение:
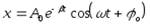
Где 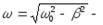

b — коэффициент затухания,
A0— амплитуда в начальный момент времени (t=0).
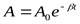
С течением времени амплитуда убывает по экспоненциальному закону (рис. 3).
Величины, характеризующие быстроту затухания колебаний: коэффициент затухания, логарифмический декремент затухания, добротность, их физический смысл.
.коэффициент затухания β.
Изменение амплитуды затухающих колебаний происходит по экспоненциальному закону:
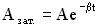
Пусть за время τ амплитуда колебаний уменьшится в “e ” раз (“е” – основание натурального логарифма, е ≈ 2,718). Тогда, с одной стороны, 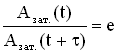
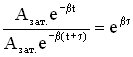
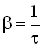
Промежуток времени τ, за который амплитуда уменьшается в “е” раз, называется временем релаксации.
Коэффициент затухания β – величина, обратно пропорциональная времени релаксации.
Логарифмический декремент затухания δ — физическая величина, численно равная натуральному логарифму отношения двух последовательных амплитуд, отстоящих по времени на период .
Если затухание невелико, т.е. Величина β мала, то амплитуда незначительно изменяется за период, и логарифмический декремент можно определить так:
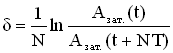
Где азат.(t) и азат.(t+nt) – амплитуды колебаний в момент времени е и через n периодов, т.е.в момент времени (t + nt).
Добротность q колебательной системы – безразмерная физическая величина, равная произведению величины (2π) νа отношение энергии w(t) системы в произвольный момент времени к убыли энергии за один период затухающих колебаний:
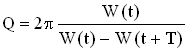
Так как энергия пропорциональна квадрату амплитуды, то
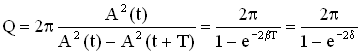
При малых значениях логарифмического декремента δ добротность колебательной системы равна
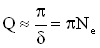
Где ne – число колебаний, за которое амплитуда уменьшается в “е” раз.
Так, добротность пружинного маятника — 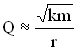
При большом коэффициенте затухания происходит не только быстрое уменьшение амплитуды, но и заметно увеличивается период колебаний. Когда сопротивление становится равным критическому , а то круговая частота обращается в нуль, а колебания прекращаются. Такой процесс называется апериодическим (рис. 1).
2. Вынужденные механические колебания. Резонанс. Резонансные кривые для амплитуды смещения.
Вынужденные механические колебания.
Колебания, совершающиеся под воздействием внешней периодической силы, называются вынужденными.
В этом случае внешняя сила совершает положительную работу и обеспечивает приток энергии к колебательной системе. Она не дает колебаниям затухать, несмотря на действие сил трения.
Периодическая внешняя сила может изменяться во времени по различным законам. Особый интерес представляет случай, когда внешняя сила, изменяющаяся по гармоническому закону с частотой ω, воздействует на колебательную систему, способную совершать собственные колебания на некоторой частоте ω0.
Если свободные колебания происходят на частоте ω0, которая определяется параметрами системы, то установившиеся вынужденные колебания всегда происходят на частоте ω внешней силы.
После начала воздействия внешней силы на колебательную систему необходимо некоторое время δt для установления вынужденных колебаний. Время установления по порядку величины равно времени затухания τ свободных колебаний в колебательной системе.
В начальный момент в колебательной системе возбуждаются оба процесса – вынужденные колебания на частоте ω и свободные колебания на собственной частоте ω0. Но свободные колебания затухают из-за неизбежного наличия сил трения. Поэтому через некоторое время в колебательной системе остаются только стационарные колебания на частоте ω внешней вынуждающей силы.
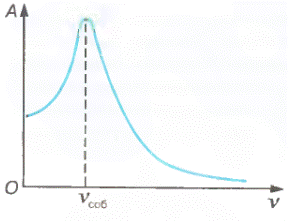
Резкое возрастание амплитуды вынужденных колебаний при ν = νcoб называется резонансом.
График зависимости амплитуды вынужденных колебаний от частоты изменения внешней силы изображен на рисунке 1. Этот график называют резонансной кривой. Максимум этой кривой приходится на частоту ν, равную собственной частоте колебаний νсоб.
Резонансные кривые для амплитуды смещения.
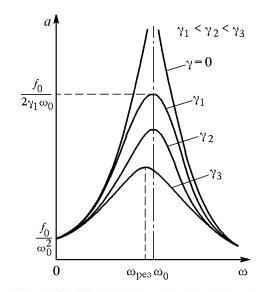
Амплитуда установившихся вынужденных колебаний пропорциональна амплитуде вынуждающей силы. Исследуем зависимость амплитуды колебаний от частоты со вынуждающей силы. При малом затухании у эта зависимость имеет очень резкий характер. Если, то при стремлении со к частоте свободных колебаний амплитуда вынужденных колебаний а стремится к бесконечности, что совпадает с полученным ранее результатом. При наличии затухания амплитуда колебаний в резонансе уже не обращается в бесконечность, хотя и значительно превышает амплитуду колебаний под действием внешней силы той же величины, но имеющей частоту, далекую от резонансной. Резонансные кривые при разных значениях постоянной затухания у приведены на рис. 1.
3. Свободные гармонические колебания в идеальном колебательном контуре.
Свободные гармонические колебания в идеальном колебательном контуре.
Среди различных электрических явлений особое место занимают электромагнитные колебания, при которых электрические величины (заряды, токи) периодически изменяются и которые сопровождаются взаимными превращениями электрического и магнитного полей. Для возбуждения и поддерживания электромагнитных колебаний используется колебательный контур — цепь, состоящая из включенных последовательно катушки индуктивностью l, конденсатора емкостью с и резистора сопротивлением r.
Рассмотрим последовательные стадии колебательного процесса в идеальном контуре, сопротивление которого пренебрежимо мало 
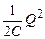
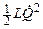
Так как 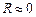
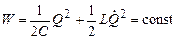
Так как она на нагревание не расходуется. Поэтому в момент 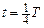
Согласно закону ома, для контура, содержащего катушку индуктивностью l, конденсатор емкостью с и резистор сопротивлением r,
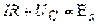
Где ir — напряжение на резисторе, uc =q/c — напряжение на конденсаторе, 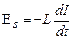
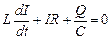
Разделив на l и подставив 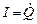
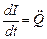
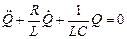
В данном колебательном контуре внешние эдс отсутствуют, поэтому рассматриваемые колебания представляют собой свободные колебания. Если контур идеальный, т.е. Сопротивление r=0, то свободные электромагнитные колебания в контуре являются гармоническими. Тогда из составленного уравнения получим дифференциальное уравнение свободных гармонических колебаний заряда в контуре
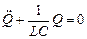
Из уравнения такого вида следует, что заряд q совершает гармонические колебания по закону
Где qm — амплитуда колебаний заряда конденсатора с циклической частотой ωо, называемой собственной частотой контура, т. Е.
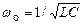
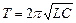
Такая формула впервые была получена у.томсоном и называется формулой томсона.
Сила тока в колебательном контуре
Где 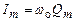
Напряжение на конденсаторе
Где 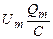
Из полученных формул вытекает, что в идеальном колебательном контуре колебания тока i опережают по фазе колебания заряда q на π/2, т. Е., когда ток достигает максимального значения, заряд (а также и напряжение обращается в нуль, и наоборот.
4. Свободные (затухающие) колебания в последовательном колебательном контуре. Величины, характеризующие быстроту затухания колебаний: коэффициент затухания, логарифмический декремент затухания, добротность, их физический смысл. Условие превращения колебаний в апериодический процесс. Критическое сопротивление.
Свободные (затухающие) колебания в последовательном колебательном контуре.
Свободные колебания в последовательном колебательном контуре.
Последовательный колебательный контур (рис. 1) содержит конденсатор емкостью c и катушку индуктивностью l и сопротивлением r. Пусть в момент времени t = 0 на конденсаторе имеется заряд 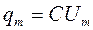
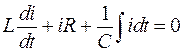 | (1) |
Учитывая, что 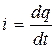
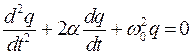 , , | (2) |
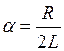 , , 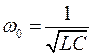 , , | (3) |
(a — коэффициент затухания, w0 – собственная частота контура).
Если 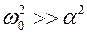
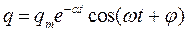 , , | (4) |
Где 
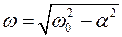
Таким образом, при 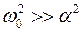
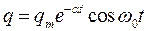 . . | (5) |
Закон изменения силы тока можно найти, дифференцируя (5) по времени с учетом, что 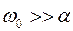
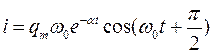 . . | (6) |
Уравнение (6) дает следующее соотношение между амплитудами тока и напряжения:
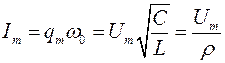
Волновое или характеристическое сопротивлением контура и является одной из его основных характеристик, так как активное сопротивление контура не влияет на соотношение между um и im; оно определяет лишь степень затухания колебаний, т.е. Быстроту уменьшения амплитуд с течением времени.
Кроме коэффициента затухания a для характеристики затухающих колебаний пользуются логарифмическим декрементом затухания, который равен натуральному логарифму отношения амплитуд колебаний, взятых через период т:
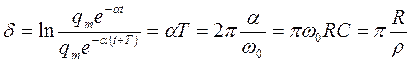 . . | (8) |
Важным параметром колебательного контура является добротность q, характеризующая относительную убыль энергии в процессе колебаний:
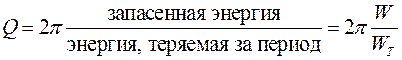 . . | (9) |
Энергия теряемая в контуре за один период, согласно закону джоуля – ленца, равна 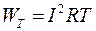
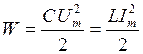
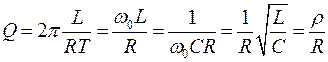 . . | (10) |
Величины, характеризующие быстроту затухания колебаний: коэффициент затухания, логарифмический декремент затухания, добротность, их физический смысл, коэффициент затухания β.
Изменение амплитуды затухающих колебаний происходит по экспоненциальному закону:
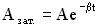
Пусть за время τ амплитуда колебаний уменьшится в “e ” раз (“е” – основание натурального логарифма, е ≈ 2,718). Тогда, с одной стороны, 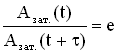
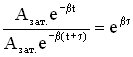
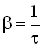
Промежуток времени τ, за который амплитуда уменьшается в “е” раз, называется временем релаксации.
Коэффициент затухания β – величина, обратно пропорциональная времени релаксации.
Логарифмический декремент затухания δ — физическая величина, численно равная натуральному логарифму отношения двух последовательных амплитуд, отстоящих по времени на период .
Если затухание невелико, т.е. Величина β мала, то амплитуда незначительно изменяется за период, и логарифмический декремент можно определить так:
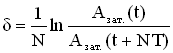
Где азат.(t) и азат.(t+nt) – амплитуды колебаний в момент времени е и через n периодов, т.е.в момент времени (t + nt).
Добротность q колебательной системы – безразмерная физическая величина, равная произведению величины (2π) νа отношение энергии w(t) системы в произвольный момент времени к убыли энергии за один период затухающих колебаний:
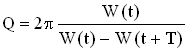
Так как энергия пропорциональна квадрату амплитуды, то
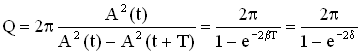
При малых значениях логарифмического декремента δ добротность колебательной системы равна
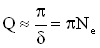
Где ne – число колебаний, за которое амплитуда уменьшается в “е” раз.
Так, добротность пружинного маятника — 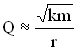
Условие превращения колебаний в апериодический процесс.
При большом коэффициенте затухания происходит не только быстрое уменьшение амплитуды, но и заметно увеличивается период колебаний. Когда сопротивление становится равным критическому , а то круговая частота обращается в нуль, а колебания прекращаются.
Чем больше сопротивление r, тем больше коэффициент затухания и тем быстрее завершается переходный процесс. При 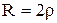
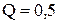
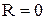
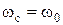
Сопротивление контура, при котором колебательный процесс переходит в апериодический, называется критическим (rкр).
Значение критического сопротивления: 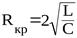
Видео:МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ период колебаний частота колебанийСкачать

Упругие и квазиупругие силы
Выясним какими силами вызываются гармонические колебания, воспользовавшись законами динамики.
По второму закону динамики сила F, действующая на материальную точку численно равна произведению массы точки m на ее ускорение w. Подставляя в это соотношение найденное ранее выражение w для гармонического колебания, определим значение силы 


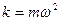
- величина силы прямо пропорциональна смещению точки от центра колебаний;
- направление силы противоположно направлению смещений, т.е. сила всегда направлена к центру (при x>0 F 0 F
При смещении материальной точки вниз от 0 на величину x на нее будет действовать сила Fупр=-kx>0 направленная вверх, т.к. x 2 =k
Эта частота колебаний называется частотой собственных колебаний системы и обозначается w0, это частота колебаний системы за счет внутренних сил.

Частота и период не зависят от амплитуды колебаний и определяются только величинами m и k. Амплитуда и фаза колебаний (или начальная фаза j0) определяются из начальных условий, при которых возникло движение.
Аналогичное гармоническое движение возникает и при движении груза m, подвешенного на пружине с учетом действия ускорения свободного падения. Отличие от рассмотренного выше случая состоит в том, что положение равновесия будет иметь место при несколько растянутой пружине. Упругая сила растяжения в положении равновесия в точности ровна силе тяжести и будет направлена вверх. Уравновешивает ее:
Чтобы материальная точка m совершала гармонические колебания не обязательно, чтобы на нее действовали именно упругие силы. Достаточно, чтобы сила при смещении от положения равновесия менялось согласно закону F=-kx.
Если сила, не являющаяся по своей природе упругой, подчиняется закону F=-mw 2 x=-kx, то она называется «квазиупругой» силой (по латыни «quasi» означает «как-бы»).
Рассмотрим пример гармонического колебательного движения под действием квазиупругих сил.
Математический маятник
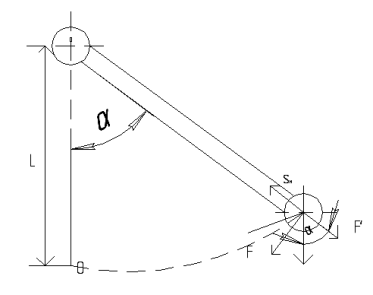
Маятник настенных часов представляет собой настенный груз, который укреплен на длинном тонком стержне, подвешенном шарнирно на горизонтальной оси C перпендикулярно стержню. В первом приближении пренебрежем массой стержня и будем считать всю массу груза m сосредоточенной в его центре М. Подобная система, состоящая из материальной точки m, подвешенная на невесомом твердом стержне или нерастяжимой нити длинны СМ=L, называется математическим маятником.
Отклоним стержень на некоторый угол a от вертикали и разложим мысленно силу веса P=mg, действующую на точку М на 2 составляющие F¢ и F, направленные соответственно вдоль стержня и перпендикулярно к нему. Сила F¢=Pcosa будет растягивать стержень и уравновесится реакцией стержня S. Неуравновешенной останется составляющая силы F=Psina. Таким образом на точку М будет действовать 2 силы P и S, направленные под углом p-a друг к другу. Равнодействующая этих сил по правилу параллелограмма будет сила F=Psina, направленная по касательной к дуге ОМ в сторону точки 0.
Когда груз придет в наинизшее положение, т.е. в точку 0, силы P и S полностью уравновесится. Таким образом точка 0 есть положение равновесия груза m. Обозначим отрезок дуги ОМ, характеризующий путь, пройденный точкой М из положения равновесия, через x и будем считать угол a и величину x положительными при отклонении стержня с грузом вправо от вертикали и отрицательными – при отклонении влево. Угол a измеряемый в радианах численно равен отношению длинны дуги x, на которую он опирается к радиусу окружности l, тогда (с учетом направления) сила F, действующая на точку М, может быть выражена в виде
Для малых углов отклонения от вертикали не превышающих 5-6°, т.е. при a
Видео:Урок 327. Гармонические колебанияСкачать

Квазиупругая и упругая сила уравнение гармонических колебаний
§2 Пружинный маятник.
Упругие и квазиупругие силы .
Уравнение колеблющейся пружины

1) величина силы пропорциональна величине отклонения системы от положения равновесия
2) направление сила противоположно направлении смещения, т.е. сила всегда направлена к положению равновесия (при х > 0, F упр F упр > 0)
3) В положении равновесия х = 0 и F упр = 0.
Систему, состоящую из материальной точки массы m и абсолютно упругой пружины с коэффициентом жесткости k , в которой возможны свободные колебания, называют пружинным маятником.
Запишем второй закон Ньютона для рис. б
Если сила не является по своей природе упругой, но подчиняется закону F = — k х , то она называется квазиупругой силой.
Получим уравнение пружинного маятника. Учтем в записи второго закона Ньютона, что
— дифференциальное уравнение точки, совершающей колебательное движение (дифференциальное уравнение пружинного маятника).
Решение дифференциального уравнения:
— уравнение колеблющейся точки (уравнение колеблющейся пружины).
— собственная частота колебаний.
§3 Математический и физический маятники.
Периоды колебаний математического и физического маятников
Математический маятник — материальная точка, подвешенная на невесомой нерастяжимой нити, и совершавшая колебания в вертикальной плоскости под действием силы тяжести. Материальная точка — тело, масса которого сосредоточена в центре масс и размерами которого в условиях данной задачи, можно пренебречь.


Основное уравнение вращательного цветения запишется в виде

М – момент сил, I – момент инерции, ε – угловое ускорение.
Равнодействующая сил 


Из треугольника АВС
таким образом, колебания математического маятника происходят под действием квазиупругой силы — силы тяжести.
Тогда (1) запишется в виде

Знак минус учитывает, что векторы 




Сократив в (2) на m и 
При малых углах колебаний α = 5 ÷6° , 
получим дифференциальное уравнение колебаний математического маятника
— уравнение математического маятника.
из которого видно, что угол α изменяется по закону косинуса. α0 — амплитуда, ω0 — циклическая частота, φ0 — начальная фаза.
— период колебаний математического маятника
Физический маятник — твердое тело, колеблющееся под действием силы тяжести вокруг неподвижной горизонтальной оси, не проходящей через центр тяжести тела, называемой осью качания маятника.

При малых углах колебаний 
— дифференциальное уравнение физического маятника.
— период колебаний физического маятника
следовательно, математический маятник с длиной
💡 Видео
Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫСкачать

Выполнялка 53.Гармонические колебания.Скачать

Физика 9 класс. §25 Гармонические колебанияСкачать

Гармонические колебания | Физика 9 класс #25 | ИнфоурокСкачать

Физика. 11 класс. Уравнение и графика гармонических колебаний /03.09.2020/Скачать

Математика это не ИсламСкачать

Физика 9 класс (Урок№11 - Гармонические колебания. Затухающие колебания. Резонанс.)Скачать

Урок 326. Динамика колебательного движенияСкачать

Гармонические колебания | Физика 11 класс #8 | ИнфоурокСкачать

Урок 325. Колебательное движение и его характеристикиСкачать

Семинар №4 "Гармонические колебания" (Чивилев В.И.)Скачать

65. Свободные гармонические колебанияСкачать

Урок 335. Анализ графика гармонических колебанийСкачать

Урок 333. "Энергетический" метод расчета частоты свободных колебанийСкачать

КОЛЕБАНИЯ физика 9 класс решение задачСкачать

Урок 330. Скорость и ускорение при гармонических колебанияхСкачать

Затухающие колебания. Вынужденные колебания | Физика 9 класс #26 | ИнфоурокСкачать