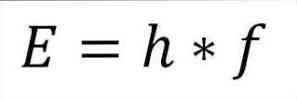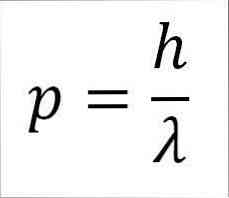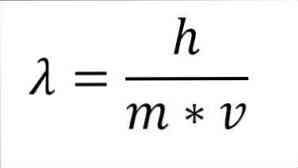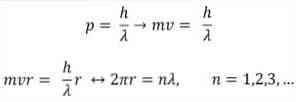Квантово механическая модель атома уравнение де бройля

Видео:Урок 450. Корпускулярно-волновой дуализм. Гипотеза де БройляСкачать

Атомная модель Де Бройля: характеристики и ограничения

Атомная модель Де Бройля: характеристики и ограничения — Наука

Видео:Волна де Бройля (видео 4) | Квантовая физика | ФизикаСкачать

Содержание:

В атомная модель де Бройля он был предложен французским физиком Луи Бройлем в 1924 году. В своей докторской диссертации Бройль утверждал дуальность электронов между частицами и волнами, заложив основы волновой механики. Бройль опубликовал важные теоретические открытия о корпускулярно-волновой природе материи на атомном уровне.

Позже утверждения де Бройля были экспериментально продемонстрированы учеными Клинтоном Дэвиссоном и Лестером Гермером в 1927 году. Теория электронных волн Де Бройля основана на предложении Эйнштейна о волновых свойствах света на коротких волнах.

Бройль объявил о возможности того, что материя имеет поведение, подобное поведению света, и предположил аналогичные свойства у субатомных частиц, таких как электроны.

Электрические заряды и орбиты ограничивают амплитуду, длину и частоту волны, описываемой электронами. Бройль объяснил движение электронов вокруг ядра атома.

Видео:Квантово-механическая модель атомаСкачать

Характеристики модели атома де Бройля

Развивая свое предложение, Бройль исходил из принципа, что электроны имеют двойную природу между волной и частицей, подобно свету.

В этом смысле Бройль провел сравнение между обоими явлениями и на основе уравнений, разработанных Эйнштейном для изучения волновой природы света, указал следующее:

— Полная энергия фотона и, следовательно, полная энергия электрона, является произведением частоты волны и постоянной Планка (6,62606957 (29) × 10 -34 Жюля x секунд), как подробно описано в следующем выражении:

В этом выражении:

E = энергия электрона.

h = постоянная Планка.

f = частота волны.

— Импульс фотона и, следовательно, электрона обратно пропорционален длине волны, и обе величины связаны через постоянную Планка:

В этом выражении:

p = импульс электрона.

h = постоянная Планка.

— Линейный импульс — это произведение массы частицы и скорости, которую частица имеет во время своего перемещения.

Если приведенное выше математическое выражение преобразовать в функцию от длины волны, мы получим следующее:

В этом выражении:

h = постоянная Планка.

m = масса электрона.

v = скорость электрона.

Поскольку h, постоянная Планка, имеет небольшое значение, длина волны λ тоже. Следовательно, можно утверждать, что волновые свойства электрона проявляются только на атомном и субатомном уровнях.

— Бройль также исходит из постулатов атомной модели Бора. Согласно последнему, орбиты электронов ограничены и могут быть только кратными целым числам. Так:

h = постоянная Планка.

m = масса электрона.

v = скорость электрона.

r = радиус орбиты.

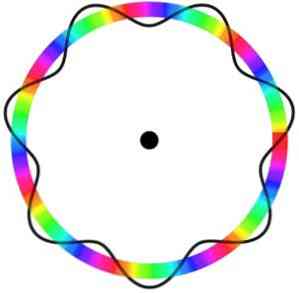
Согласно атомной модели Бора, которую Бройль принял за основу, если электроны ведут себя как стоячие волны, единственными допустимыми орбитами являются те, радиус которых равен целому кратному длине волны λ.

Следовательно, не все орбиты соответствуют параметрам, необходимым для движения электрона по ним. Вот почему электроны могут двигаться только по определенным орбитам.

Теория электронных волн де Бройля оправдала успех атомной модели Бора в объяснении поведения одного электрона атома водорода.

Точно так же это также пролило свет на то, почему эта модель не подходит для более сложных систем, то есть атомов с более чем одним электроном.

Видео:Волновая функция (видео 5) | Квантовая физика | ФизикаСкачать

Эксперимент Дэвиссона и Гермера

Экспериментальная проверка атомной модели де Бройля состоялась через 3 года после ее публикации, в 1927 году.

Выдающиеся американские физики Клинтон Дж. Дэвиссон и Лестер Гермер экспериментально подтвердили теорию волновой механики.

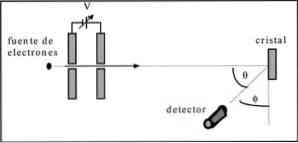
Дэвиссон и Гермер провели испытания на рассеяние электронного луча через кристалл никеля и наблюдали явление дифракции через металлическую среду.

Проведенный эксперимент заключался в проведении следующей процедуры:

— В первую очередь был размещен узел электронного пучка с известной начальной энергией.

— Установлен источник напряжения для ускорения движения электронов за счет разности потенциалов.

— поток электронного луча был направлен на металлический кристалл; в данном случае никель.

— Было измерено количество электронов, столкнувшихся с кристаллом никеля.

В конце эксперимента Дэвиссон и Гермер обнаружили, что электроны рассеиваются в разных направлениях.

Повторяя эксперимент с использованием металлических кристаллов разной ориентации, ученые обнаружили следующее:

— Рассеяние электронного луча через металлический кристалл было сопоставимо с явлением интерференции и дифракции световых лучей.

— Отражение электронов от ударного кристалла описывало траекторию, которую он теоретически должен описывать согласно теории электронных волн де Бройля.

Короче говоря, эксперимент Дэвиссона и Гермера экспериментально подтвердил дуальную волновую и частичную природу электронов.

Видео:11. Строение атома. Квантовые числаСкачать

Ограничения

Атомная модель де Бройля не предсказывает точное положение электрона на орбите, по которой он движется.

В этой модели электроны воспринимаются как волны, которые движутся по орбите без определенного местоположения, тем самым вводя понятие электронной орбитали.

Более того, модель атома де Бройля, аналогичная модели Шредингера, не рассматривает вращение электронов вокруг своей оси (вращение).

Пренебрегая собственным угловым моментом электронов, мы пренебрегаем пространственными вариациями этих субатомных частиц.

Точно так же эта модель также не учитывает изменения в поведении быстрых электронов как следствие релятивистских эффектов.

Видео:СТРОЕНИЕ АТОМА ХИМИЯ 8 класс // Подготовка к ЕГЭ по Химии - INTENSIVСкачать

Интересные статьи

Атомная модель Шредингера.

Атомная модель Чедвика.

Модель атома Гейзенберга.

Атомная модель Перрина.

Атомная модель Томсона.

Атомная модель Дальтона.

Атомная модель Дирака Джордана.

Атомная модель Демокрита.

Атомная модель Левкиппа.

Атомная модель Бора.

Текущая атомная модель.

Видео:Лучшая модель атома? [Минутка физики]Скачать

Ссылки

1. Квантовая теория Бора и волны Де Бройля (н.д.). Получено с: ne.phys.kyushu-u.ac.j
2. Луи де Бройль — Биографический (1929). © Нобелевский фонд. Получено с: nobelprize.org
3. Луи-Виктор де Бройль (s.f.). Получено с: chemed.chem.purdue.edu
4. Ловетт, Б. (1998). Луи де Бройль. Encyclopdia Britannica, Inc. Получено с: britannica.com
5. Атомная модель де Бройля. Национальный университет дистанционного образования. Испания. Получено с: ocw.innova.uned.es
6. Волны материи Луи де Бройля (s.f.). Получено с: hiru.eus
7. Фон Памель О. и Маркизио С. (s.f.). Квантовая механика. Национальный университет Росарио. Получено с: fceia.unr.edu.ar

Ganoderma lucidum: характеристики, среда обитания и польза

Боязнь тараканов (блатофобия): причины, симптомы и последствия

Видео:Квантовые числа. 1 часть. 10 класс.Скачать

Квантово-механическая модель строения атома. Корпускулярно-волновые свойства электрона: уравнение Де Бройля, принцип неопределенности Гейзенберга (стр. 1 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7

В 1911г. Э. Резерфорд предложил модель атома, согласно которой атом состоит из положительно заряженного ядра, в котором находится почти вся масса атома, и располагающихся вокруг ядра электронов. Ядро состоит из протонов и нейтронов. Число электронов равно числу протонов и, поэтому, атом электронейтрален.

В основе квантово-механической теории строения атомов лежат их корпускулярно-волновые свойства. С движущимся электроном ассоциируется волна, длина которой определяется уравнением Де-Бройля: где λ — длина волны, (м); m — масса электрона; V-скорость движения частицы (≈108 м/с), h — постоянная Планка. Принцип неопределенности Гейзенберга: невозможно описать с высокой степенью точности местонахождение электрона (координаты), и его энергию (импульс) в один и тот же момент времени.

2. Уравнение Шредингера. Квантовые числа, волновая функция, понятие об атомной орбитали.

Уравнение Шрёдингера (1926 г) описывает волновые и корпускулярные свойства электрона в атоме водорода. Решениями уравнения Шредингера являются энергии электрона и волновая функция ψ(пси).

Волновая функция ψ зависит от координат (x, y, z), и энергии E электрона и не имеет определенного физического толкования. Квадрат волновой функции ψ2 определяет плотность вероятности нахождения электрона в точке с координатами (x, y, z). ψ2·ΔV –вероятность нахождения электрона в данном объеме атома ΔV. Чем больше ψ2·ΔV, тем плотнее электронное облако в данном объеме атома.

Область пространства, в которой вероятность нахождения электрона составляет не менее 90%, называют атомной орбиталью. Атомные орбитали различаются по энергии, размерам, форме, ориентации в пространстве и могут быть охарактеризованы тремя квантовыми числами (n, l, ml).

Главное квантовое число характеризует энергию электрона в атоме. принимает только целые положительные значения n = 1, 2, 3…∞. С увеличением n энергия и размер электронного облака (атомной орбитали) возрастает. Совокупность атомных орбиталей с одинаковым значением n называют уровнем или электронным слоем.

Орбитальное квантовое число l принимает значения от 0 до (n-1), например, при n = 3: l = 0, 1, 2. Характеризует форму атомных орбиталей (электронных облаков), для которых в зависимости от l приняты соответствующие обозначения: l 0, 1, 2, 3, 4, 5…

обозначение s, p, d, f, g, h…

Магнитное квантовое число определяет возможные ориентации электронного облака в пространстве. ml – может принимать положительные и отрицательные целочисленные значения от –l до +l через нуль. Так, для s — орбиталей (l = 0, ml = 0), возможна одна ориентация. Для р — орбиталей (l=1, ml = -1, 0, +1), что соответствует трем ориентациям р — орбиталей относительно трех осей. Для d — орбиталей (l=2, ml = -2, -1, 0, +1, +2) число возможных ориентаций – пять, для f – орбиталей — семь.

Спиновое (ms) квантовое число характеризует сложное движение электрона вокруг собственной оси; принимает значения +1/2 и –1/2.

3. Энергетическая диаграмма возможных состояний электрона в атоме водорода.

4. Распределение электронов по АО в многоэлектронных атомах. Принцип Паули, правило Гунда, правила Клечковского.

Распределение электронов в многоэлектронных атомах основано на трех положениях: принципе минимума энергии, принципе В. Паули и правиле Ф. Хунда.

Принцип наименьшей энергии. Электроны занимают в атоме орбитали с наименьшей энергией. Последовательность расположения АО по уровням энергии при заполнении электронами определяется правилом Клечковского: электроны в невозбужденном атоме располагаются в состояниях, где меньше сумма (n+l), так как энергия электронов зависит от n и l и не зависит от ml и ms. При одинаковом значении этой суммы в первую очередь заполняется орбиталь с меньшим значением главного квантового числа (n).

Принцип Паули. В атоме не может быть двух электронов, имеющих четыре одинаковых квантовых числа. Один электрон от другого на атомной орбитали должен отличаться спиновым квантовым числом. Как следует из принципа Паули, на атомной орбитали максимально может быть два электрона, отличающихся спином и это обозначается: ↑↓.

Правило Хунда. При заполнении энергетического подуровня, электроны стремятся заполнить свободные орбитали, сначала по одному с параллельными спинами, а затем по второму с противоположными спинами.

5. Периодический закон. Периодическая система. Электронные конфигурации атомов.

Периодический закон: свойства простых веществ, а также формы и свойства соединений элементов находятся в периодической зависимости от заряда ядра атомов элементов.

Периодическую систему химических элементов в настоящее время рассматривают как классификацию элементов в зависимости от зарядов ядра и от строения электронных оболочек невозбужденных атомов. Распределение электронов по атомным орбиталям называют электронной конфигурацией атома. И представляют в виде а) полной электронной формулы, например: 22Ti 1s22s22p63s23p64s23d2; б) краткой электронной формулы: 22Ti [Ar]4s23d2; в) электроно-графической формулы, в которой атомные орбитали обозначают в виде клеток (энергетических или квантовых ячеек), а электроны – стрелками ↑↓.

6. Периодические свойства атомов (радиусы атомов, энергия ионизации, сродство к электрону, электроотрицательность).

— атомный и ионный радиусы (r), определяемые как средние радиусы атома или иона, находимые из экспериментальных данных по межатомным расстояниям в различных соединениях;

— энергия ионизации, определяемая количеством энергии, необходимой для отрыва электрона от атома ();

— сродство к электрону, определяемое количеством энергии, выделяющейся при присоединении дополнительного электрона к атому ();

— Электроотрицательность (χ) — фундаментальное химическое свойство атома, количественная характеристика способности атома в молекуле притягивать к себе общие электронные пары.

7. Характерные степени окисления элементов.

Степень окисления — условный заряд атома в молекуле, вычисленный в предположении, что все связи имеют ионный характер. Понятие степени окисления введено в предположении о пол­ном смещении пар электронов к тому или другому атому (показывая при этом заряд ионов, образующих ионное соедине­ние). Поэтому следует помнить, что в полярных соединениях сте­пень окисления означает число электронов, лишь смещенных от данного атома к атому, связанному с ним.

8. Ковалентная химическая связь: механизмы её образования, разновидности. Длина, энергия, порядок (кратность) ковалентной связи.

Связь, образованную посредством перекрывания электронных облаков, то есть осуществляемую общей парой электронов с противоположными спинами, называют ковалентной связью.

Для объяснения природы ковалентной связи и механизма ее образования используются два метода – метод валентных связей (ВС) и метод молекулярных орбиталей (МО). В основе метода ВС лежит теория Льюиса об образовании ковалентной связи формированием общей пары электронов между взаимодействующими атомами. Основные характеристики ковалентной химической связи – длина связи, энергия связи. С увеличением кратности связи уменьшается длина связи и увеличивается суммарная энергия связи.

9, 10. Насыщаемость ковалентной связи и валентные возможности атомов.

Направленность ковалентной связи и геометрия молекулы.

Ковалентной связи присущи следующие особенности – насыщаемость и направленность. Насыщаемость определяет стехиометрию молекулярных химических соединений (формульный состав, массовые соотношения элементов) и валентные возможности атомов (способность образовать ограниченное число ковалентных связей).

Направленность ковалентной связи определяет геометрическую структуру (форму) молекулы. Атомные орбитали имеют разные формы и размеры, разную ориентированность в пространстве, и перекрываются по определенным, предпочтительным направлениям, в которых достигается максимальная плотность перекрывания. Это приводит к образованию молекулы определенной геометрической формы (линейной, угловой, тетраэдрической и др). Например, атом серы в сероводороде образует связи с атомами водорода за счет p-электронов, ориентированных вдоль осей координат под углом 90о.

11. Полярность и поляризуемость ковалентной связи. Полярность молекулы.

Связь в двухатомных молекулах, образованная из одинаковых атомов (Н2) или атомов близких по электроотрицательности (ЭО), называется неполярной (гомеополярной). Связь, образованная различными атомами, отличающимися ЭО, называется полярной (гетерополярной).

Полярность связи обуславливается различием ЭО и размеров атомов. Полярность связи обуславливает полярность молекулы – то есть несимметричное распределение электронной плотности, при котором «центры тяжести положительных и отрицательных зарядов» в молекуле не будут совпадать в одной точке. Поляризуемостью ковалентной связи и (или) молекулы называют ее способность под действием внешнего электрического поля становиться полярной или более полярной. Поляризуемость π-связи выше, чем поляризуемость σ-связи. Поляризуемость молекулы возрастает с увеличением ее объема и числа π-связей.

12. Металлическая связь. Деление элементов на металлы и неметаллы. Металлические структуры.

Металлическая связь — химическая связь, обусловленная наличием относительно свободных электронов. Металлическая связь возникает в металлах, сплавах, интерметаллических соединениях. Валентные электроны внешних оболочек металла относительно легко удаляются, из атомов образуются катионы металла. Электроны делокализованы и могут свободно перемещаться по всему кристаллу. Оставшиеся катионы металлов притягиваются делокализованным электронным облаком («электронным газом»), заполняющим пространство между ними. Образованную подобным образом химическую связь называют металлической связью. Металлическая связь характеризуется ненаправленностью и ненасыщаемостью. Строение металлических кристаллов наиболее точно описывается «структурами с плотнейшей укладкой шаров».

Видео:Физика 11 класс (Урок№25 - Квантовые постулаты Бора.)Скачать

Характеристики и ограничения атомной модели Бройля

Атомная модель Бройля был предложен французским физиком Луи Бройлем в 1924 году. В своей докторской диссертации Бройль утверждал, что электронно-волновое дуальность электронов закладывает основы волновой механики. Бройль опубликовал важные теоретические выводы о корпускулярно-волновой природе вещества в атомном масштабе..

Впоследствии утверждения Бройля были экспериментально продемонстрированы учеными Клинтоном Дэвиссоном и Лестером Джермером в 1927 году. Теория электронных волн Бройля основана на предложении Эйнштейна о волновых свойствах света на коротких длинах волн..

Брогли объявил о возможности поведения вещества, подобного поведению света, и предложил аналогичные свойства в субатомных частицах, таких как электроны..

Электрические заряды и орбиты ограничивают амплитуду, длину и частоту волны, описываемой электронами. Бройль объяснил движение электронов вокруг атомного ядра.

• 1 Характеристики атомной модели Бройля
• 2 Эксперимент Дэвиссона и Гермера
• 3 ограничения
• 4 Статьи интересов
• 5 ссылок

Видео:Теория Бора. Гипотеза де Бройля. Принцип неопределенности. Уравнение Шрёдингера.Скачать

Характеристики атомной модели Бройля

Чтобы развить свое предложение, Бройль исходил из принципа, что электроны имеют двойственную природу между волной и частицей, подобно свету..

В этом смысле Бройль провел сравнение между обоими явлениями и, основываясь на уравнениях, разработанных Эйнштейном для изучения волновой природы света, указал следующее:

— Полная энергия фотона и, следовательно, полная энергия электрона, являются результатом произведения частоты волны и постоянной Планка (6.62606957 (29) × 10 -34 Жюль х секунд), как указано в следующем выражении:

В этом выражении:

E = энергия электрона.

h = постоянная планки.

f = частота волны.

— Линейный момент фотона, а следовательно, и электрона, обратно пропорционален длине волны, и обе величины связаны через постоянную Планка:

В этом выражении:

р = линейный момент электрона.

h = постоянная планки.

— Линейный импульс представляет собой произведение массы частицы на скорость, которую частица имеет при перемещении.

Если предыдущее математическое выражение реструктурируется как функция длины волны, мы имеем следующее:

В указанном выражении:

h = постоянная планки.

m = масса электрона.

v = скорость электрона.

Поскольку h, постоянная Планка, имеет небольшое значение, длина волны λ также. Следовательно, можно утверждать, что волновые свойства электрона проявляются только на атомном и субатомном уровнях..

— Бройль также основан на постулатах атомной модели Бора. Согласно последним, орбиты электронов ограничены и могут быть только кратными целым числам. таким образом:

h = постоянная планки.

m = масса электрона.

v = скорость электрона.

r = радиус орбиты.

Согласно атомной модели Бора, которую Брогли принял за основу, если электроны ведут себя как стоячие волны, единственными допустимыми орбитами являются те, радиус которых равен целому кратному длине волны λ.

Поэтому не все орбиты соответствуют параметрам, необходимым для того, чтобы электрон проходил через них. Вот почему электроны могут путешествовать только по определенным орбитам.

Волновая теория электронов Бройля обосновала успех атомной модели Бора для объяснения поведения одиночного электрона атома водорода..

Аналогично, это также пролило свет на то, почему эта модель не подходит для более сложных систем, то есть атомов с более чем одним электроном..

Видео:Урок 459. Обзор квантовой теории атома водородаСкачать

Эксперимент Дэвиссона и Гермера

Экспериментальная проверка атомной модели Брогли состоялась через 3 года после ее публикации, в 1927 году..

Выдающиеся американские физики Клинтон Дж. Дэвиссон и Лестер Гермер экспериментально подтвердили теорию волновой механики.

Дэвиссон и Гермер провели тесты рассеяния электронного пучка на кристалле никеля и наблюдали явление дифракции в металлической среде..

Проведенный эксперимент состоял из проведения следующей процедуры:

— В первом случае была размещена сборка с электронным пучком, которая имела известную начальную энергию.

— Источник напряжения был установлен, чтобы ускорить движение электронов, вызывая разность потенциалов.

— Поток электронного пучка был направлен к металлическому кристаллу; в этом случае никель.

— Было измерено количество электронов, которые воздействовали на кристалл никеля..

В конце эксперимента Дэвиссон и Гермер обнаружили, что электроны были распределены в разных направлениях..

Повторяя эксперимент с использованием металлических кристаллов с различной ориентацией, ученые обнаружили следующее:

— Дисперсия электронного пучка через металлический кристалл была сравнима с явлением интерференции и дифракции световых лучей..

— Отражение электронов на ударном кристалле описало траекторию, которую, теоретически, следует описать в соответствии с теорией электронных волн Бройля.

В синтезе эксперимент Дэвиссона и Гермера экспериментально доказал двойственную волновую-электронную природу электронов.

Видео:Квантовые постулаты Бора. Модель атома | Физика 11 класс #43 | ИнфоурокСкачать

ограничения

Модель атома Брогли не предсказывает точное местоположение электрона на орбите, по которой он движется.

В этой модели электроны воспринимаются как волны, которые движутся по орбите без определенного местоположения, что вводит понятие электронной орбитали.

Кроме того, модель атома Бройля, аналогичная модели Шредингера, не учитывает вращение электронов вокруг своей оси (спин).

Игнорируя внутренний момент импульса электронов, пространственные изменения этих субатомных частиц игнорируются..

В том же порядке идей, эта модель не учитывает изменения в поведении быстрых электронов в результате релятивистских эффектов.

📸 Видео

Волновые свойства частиц. Волны де Бройля. 11 класс.Скачать

ВОЛНА ДЕ БРОЙЛЯ. ДИФРАКЦИЯ ЭЛЕКТРОНОВ. ОПЫТ ТОМСОНА. | КВАНТОВАЯ ФИЗИКА - АВАКЯНЦ Л. П. ФизФак МГУСкачать

Структура материи (эпизод 4): модель Бора и гипотеза де Бройля – физик Виталий Бейлин | НаучпопСкачать

Устройство атома от Томсона до ШрёдингераСкачать

Квантовые числа (видео 14) | Квантовая физика | ФизикаСкачать

Консультация по квантовой механике. Часть 4. "Волны де Бройля. Дифракция частиц"Скачать

Урок 455. Уравнение ШрёдингераСкачать

Современная квантовая модель атомаСкачать