Квадратные уравнения вида ах2 вх с (2 видео)

Содержание

Неполные квадратные уравнения
Основные понятия
Решение неполных квадратных уравнений
Как решить уравнение ax² = 0
Как решить уравнение ax² + с = 0
В двух словах
Как решить уравнение ax² + bx = 0
Квадратные уравнения. Углубленное изучение свойств квадратных уравнений
Алгебра. 8 класс
💥 Видео

Видео:Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

Неполные квадратные уравнения

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Видео:Квадратные уравнения от «А» до «Я». Классификация, решение и теорема Виета | МатематикаСкачать

Основные понятия

Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.

Степень уравнения можно определить по наибольшей степени, в которой стоит неизвестное. Если неизвестное стоит во второй степени — это квадратное уравнение.

Квадратное уравнение — это ax² + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.

Чтобы определить, сколько корней имеет уравнение, нужно обратить внимание на дискриминант. Чтобы его найти, берем формулу: D = b² − 4ac. А вот свойства дискриминанта:

если D 0, есть два различных корня.

Неполное квадратное уравнение — это уравнение вида ax² + bx + c = 0, где хотя бы один из коэффициентов b или c равен нулю.

Неполные квадратные уравнения бывают трех видов:

Если b = 0, то квадратное уравнение принимает вид ax² + 0x+c=0 и оно равносильно ax² + c = 0.
Если c = 0, то квадратное уравнение выглядит так ax² + bx + 0 = 0, иначе его можно написать как ax² + bx = 0.
Если b = 0 и c = 0, то квадратное уравнение выглядит так ax² = 0.

Такие уравнения отличаются от полного квадратного тем, что их левые части не содержат слагаемого с неизвестной переменной, либо свободного члена, либо и того и другого. Отсюда и их название — неполные квадратные уравнения.

Видео:Неполные квадратные уравнения. Алгебра, 8 классСкачать

Решение неполных квадратных уравнений

Как мы уже знаем, есть три формулы неполных квадратных уравнений:

ax² = 0, ему отвечают коэффициенты b = 0 и c = 0;
ax² + c = 0, при b = 0;
ax² + bx = 0, при c = 0.

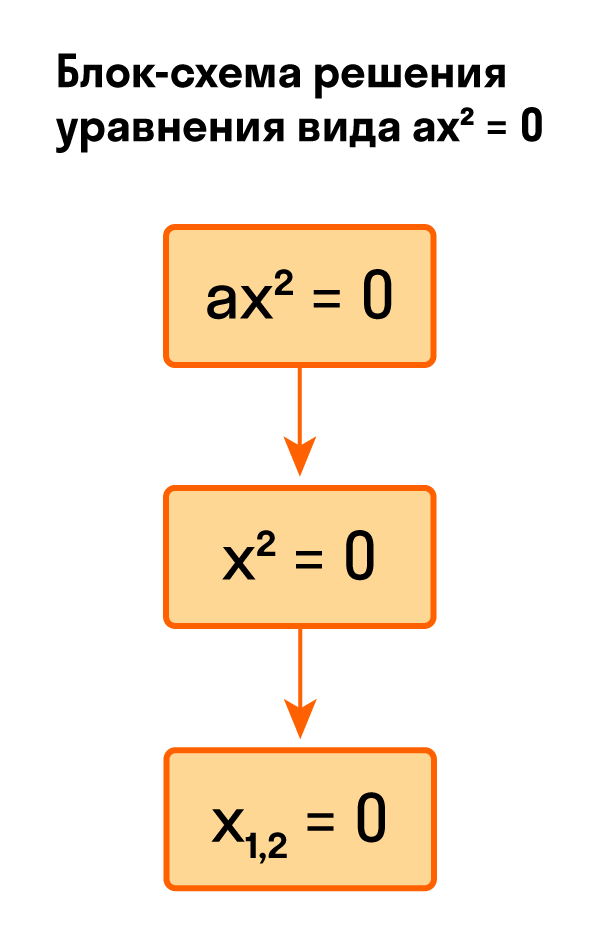
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).

Видео:Квадратное уравнение. 8 класс.Скачать

Как решить уравнение ax² = 0

Начнем с решения неполных квадратных уравнений, в которых b и c равны нулю, то есть, с уравнений вида ax² = 0.

Уравнение ax² = 0 равносильно x² = 0. Такое преобразование возможно, когда мы разделили обе части на некое число a, которое не равно нулю. Корнем уравнения x² = 0 является нуль, так как 0² = 0. Других корней у этого уравнения нет, что подтверждают свойства степеней.

Таким образом, неполное квадратное уравнение ax² = 0 имеет единственный корень x = 0.

Пример 1. Решить −5x² = 0.

Замечаем, что данному уравнению равносильно x2 = 0, значит исходное уравнение имеет единственный корень — нуль.
По шагам решение выглядит так:

Записывайся на дополнительные уроки по математике онлайн, с нашими лучшими преподавателями! Для учеников с 1 по 11 класса!

Видео:Алгебра 8. Урок 9 - Квадратные уравнения. Полные и неполныеСкачать

Как решить уравнение ax² + с = 0

Обратим внимание на неполные квадратные уравнения вида ax² + c = 0, в которых b = 0, c ≠ 0. Мы знаем, что слагаемые в уравнениях носят двусторонние куртки: когда мы переносим их из одной части уравнения в другую, они надевает куртку на другую сторону — меняют знак на противоположный.

Еще мы знаем, что если обе части уравнения поделить на одно и то же число (кроме нуля) — у нас получится равносильное уравнение. То есть одно и то же, только с другими цифрами.

Держим все это в голове и колдуем над неполным квадратным уравнением (производим «равносильные преобразования»): ax² + c = 0:

перенесем c в правую часть: ax² = — c,
разделим обе части на a: x² = — c/а.

Ну все, теперь мы готовы к выводам о корнях неполного квадратного уравнения. В зависимости от значений a и c, выражение — c/а может быть отрицательным или положительным. Разберем конкретные случаи.

Если — c/а 0, то корни уравнения x² = — c/а будут другими. Например, можно использовать правило квадратного корня и тогда корень уравнения равен числу √- c/а, так как (√- c/а)² = — c/а. Кроме того, корнем уравнения может стать -√- c/а, так как (-√- c/а)² = — c/а. Ура, больше у этого уравнения нет корней.

В двух словах

Неполное квадратное уравнение ax² + c = 0 равносильно уравнению ax² + c = 0, которое:

не имеет корней при — c/а 0.

Пример 1. Найти решение уравнения 9x² + 4 = 0.

Разделим обе части на 9:

В правой части осталось число со знаком минус, значит у данного уравнения нет корней.

Ответ: уравнение 9x² + 4 = 0 не имеет корней.

Пример 2. Решить -x² + 9 = 0.

Разделим обе части на -1:

Ответ: уравнение -x² + 9 = 0 имеет два корня -3; 3.

Видео:Алгебра 8 класс (Урок№28 - Решение квадратных уравнений вида ax2 + bx + c = 0.Формула корней кв.ур.)Скачать

Как решить уравнение ax² + bx = 0

Осталось разобрать третий вид неполных квадратных уравнений, когда c = 0.

Квадратное уравнение без с непривычно решать только первые несколько примеров. Запомнив алгоритм, будет значительно проще щелкать задачки из учебника.

Неполное квадратное уравнение ax² + bx = 0 можно решить методом разложения на множители. Разложим на множители многочлен, который расположен в левой части уравнения — вынесем за скобки общий множитель x.

Теперь можем перейти от исходного уравнения к равносильному x * (ax + b) = 0. А это уравнение равносильно совокупности двух уравнений x = 0 и ax + b = 0, последнее — линейное, его корень x = −b/a.

Таким образом, неполное квадратное уравнение ax² + bx = 0 имеет два корня:

Пример 1. Решить уравнение 2x² — 32x = 0

Это уравнение равносильно х = 0 и 2x — 32 = 0.

Решить линейное уравнение:

Значит корни исходного уравнения — 0 и 16.

Ответ: х = 0 и х = 16.

Пример 2. Решить уравнение 3x² — 12x = 0

Разложить левую часть уравнения на множители и найти корни:

Видео:Решение биквадратных уравнений. 8 класс.Скачать

Квадратные уравнения. Углубленное изучение свойств квадратных уравнений

Разделы: Математика

Тип урока: урок обобщения и систематизации знаний, углубленное изучение свойств квадратных уравнений.

Образовательные цели урока: обеспечить закрепление теоремы Виета, обратить внимание учащихся на решение квадратных уравнений ах 2 + вх + с = 0, в которых а+в+с=0; привить навыки устного решения таких уравнений.

Воспитательные цели урока: способствовать выработке у школьников желания и потребности обобщения изучаемых фактов, развивать самостоятельность и творчество.

Ход урока

1. Организационный момент.

Учащимся сообщаются задачи урока:

Контроль знаний с помощью тестирования (тест на заполнение пропусков, чтобы получилось верное определение, формулировка, правило)
Решение задач на применение прямой и обратной теорем Виета.
Изучение нового свойства квадратных уравнений.

2. Повторение пройденного материала.

1) Решить уравнение (работа у доски): 7х 2 — 9х + 2 =0

Решение: D = в 2 – 4ас, D = 25, х₁ = , х₂ = 1. Ответ: х₁ = , х₂ = 1.

2) Тест “ Квадратные уравнения”:

Вариант 1

. уравнением называется уравнение ах 2 + вх + с = 0, где а,в,с – заданные числа, а 0, х – переменная.
Уравнение х 2 = а, где а > 0, имеет корни х₁ = . ; х₂ = .
Уравнение ах 2 = 0, где а 0, называется . .
Уравнение ах 2 + вх + с = 0, где а 0, в 0, называется . квадратным уравнением.
Если ах 2 + вх + с = 0 — квадратное уравнение (а 0), то “в” называют . коэффициентом.
Корни квадратного уравнения ах 2 + вх + с = 0 вычисляют по формуле х = . .
Приведенное квадратное уравнение х 2 + рх + q = 0 совпадает с уравнением общего вида, в котором а = . в = . с = . .
Если х₁ и х₂ — корни уравнения х 2 + рх + q = 0, то справедливы формулы х₁ + х₂ =. ; х₁ * х₂ = .

Вариант 2

Если ах 2 + вх + с = 0 — квадратное уравнение, то а называют . коэффициентом, с — . членом.
Уравнение х 2 = а, где а 2 + с = 0, где а 0, с 0, называется . квадратным уравнением.
Корни квадратного уравнения ах 2 + вх + с = 0 вычисляют по формуле х₁ = . ; х₂ = . .
Квадратное уравнение ах 2 + вх + с = 0 имеет два различных действительных корня, если в 2 – 4ас . 0.
Квадратное уравнение вида х 2 + рх + q = 0 называют . .
Сумма корней приведенного квадратного уравнения равна . коэффициенту, взятому с . знаком, а произведение корней равно . числу.
Если числа p, q, х_1, х ₂ таковы, что х₁ + х₂ = — Р; х₁ * х₂ = . то х₁ и х₂ — корни уравнения.

3. Задание на определение вида уравнения (устно).

— Ребята, здесь вы видите уравнения, определенные по какому-то признаку. Как вы думаете, какое из уравнений этой группы является лишним?

Видео:5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

Алгебра. 8 класс

Квадратные уравнения можно решать методом выделения квадрата двучлена.

Напомним формулы квадрата разности и квадрата суммы.

Рассмотрим уравнение 5x 2 – 6x + 1 = 0.

Преобразуем к приведённому виду. Разделим на 5 обе части уравнения:

Второй коэффициент представим в виде произведения:

Для выделения квадрата двучлена не хватает квадрата вычитаемого. Прибавим выражение к разности и, чтобы ничего не изменилось, вычтем его же:

Преобразуем уравнение в квадрат двучлена:

Перенеся слагаемые таким образом, чтобы в левой части был квадрат разности, а справа от знака равенства находилось свободное число, получим:

Извлечение корня из квадрата приводит к двум линейным уравнениям:
или .

В итоге получим x = 1 или x = 0,2.

Алгоритм решение квадратного уравнения в общем виде

Деление на первый коэффициент квадратного трёхчлена – получение приведённого квадратного уравнения:

Получение уравнения вида – квадрат многочлена слева, свободное число справа:

Приведение к общему знаменателю:

Число корней этого уравнения зависит от знака правой части.

4a 2 > 0, значит, знак дроби зависит от знака выражения b 2 – 4ac.

Возможны три случая.

1. D = b 2 – 4ac 2 – 4ac = 0.
Уравнение принимает вид , очевидно, что . Т. е. квадратное уравнение имеет один корень.

3. D = b 2 – 4ac > 0.
или .
Получим два корня:
или .

Формула корней квадратного уравнения

, где D = b 2 – 4ac.

Итак, чтобы решить квадратное уравнение необходимо найти его дискриминант. Если он будет отрицательным, то сделать вывод, что корней нет. Если дискриминант окажется положительным или равным нулю, то корни можно будет найти, используя формулу корней квадратного уравнения.

Решим уравнение 5x 2 – 6x + 1 = 0.

D = b 2 – 4ac = (–6) 2 – 4 • 5 • 1 = 36 – 20 = 16 > 0.
Значит, уравнение имеет два корня.

Т. е. x₁ = 0,2; x₂ = 1.

Отдельно выделяют квадратные уравнения, у которых второй коэффициент является чётным числом.

D₁ = k 2 – ac
1. D₁ = k 2 – ac 2 – ac ≥ 0. Корни уравнения: .

Алгебра. 8 класс: учеб. для общеобразоват. организаций / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. – 6-е изд. – М.: Просвещение, 2017.