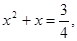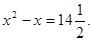Квадратные уравнения в школьном курсе математики (8 видео)

Роль и место квадратных уравнений в образовательном процессе школьников

2014г. ученица 9 Б класса

Тема: «Роль и место квадратных уравнений в образовательном процессе школьников»

(проблемно –исследовательская работа)

Содержание

Скачать:
Предварительный просмотр:
Курсовая работа: Формирование умения решения квадратных уравнений в 8 классе
Курсовая работа
Как решать квадратные уравнения
Понятие квадратного уравнения
Приведенные и неприведенные квадратные уравнения
Полные и неполные квадратные уравнения
Решение неполных квадратных уравнений
Как решить уравнение ax 2 = 0
Как решить уравнение ax 2 + с = 0
Как решить уравнение ax 2 + bx = 0
Как разложить квадратное уравнение
Дискриминант: формула корней квадратного уравнения
Алгоритм решения квадратных уравнений по формулам корней
Примеры решения квадратных уравнений
Формула корней для четных вторых коэффициентов
Формула Виета
Упрощаем вид квадратных уравнений
Связь между корнями и коэффициентами
📸 Видео

Видео:Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

Скачать:

Вложение	Размер
gagarina_rol_i_mesto_ka_uravn.doc	349.5 КБ

Видео:Быстрый способ решения квадратного уравненияСкачать

Предварительный просмотр:

Муниципальное бюджетное общеобразовательное учреждение

средняя общеобразовательная школа №9 г. Холмска

муниципального образования «Холмский городской округ»

Тема: «Роль и место квадратных уравнений в образовательном процессе школьников»

(проблемно –исследовательская работа)

ученица 9-б класса

Руководитель: учитель математики

Глава 1.История квадратных уравнений. 5

Глава 2.Математичская модель — квадратные уравнения и его корни. 8

Неполное квадратное уравнение; 8
Метод выделения полного квадрата; 8
Решение квадратных уравнений по формуле; 9
Теорема Виета; 10
Биквадратные уравнения. 11

Глава 3.Приёмы устного решения квадратного уравнения. 12

3.1 Свойства коэффициентов квадратного уравнения; 12

3.2 Приём «Переброски». 13

Глава 4.Квадратные уравнения в предметах естественно-математического цикла. 14

Глава 5.Комплексные числа. 15

Список литературы. 17

Ресурсы Интернета. 17

« Мне приходилось делить свое время между политикой и уравнениями . однако уравнения, по –моему, гораздо важнее, потому что политика существует только для данного момента, а уравнения будут существовать вечно.»

Школьник начальных классов, только приступивший к изучению арифметики, скажет, что математика изучает правила счёта предметов, школьники постарше добавит к сказанному, что в понятие математики входят алгебра и геометрия, а выпускники средней школы включат в определение математики ещё изучение тригонометрии, вычисление производных и интеграла.

Любой восьмиклассник нашей школы особенно выделит, что математика изучает квадратные уравнения.

После изучения темы: Квадратные уравнения» наша учительница по математике Л.И. Рязанцева проводит урок- отчёт. И вот какое стихотворение написал один из её учеников:

Квадратным уравнениям посвящается

Ах, уравнения, квадратные,

вы такие разные – распрекрасные

полные, неполные, приведенные.

Коэффициент у вас буквы латинские –

а, в и с величаемы.

И пути решения у всех разные –

разложи, перенеси, дискриминант найди.

А дискриминант в² — 4ас формула особая,

к полному и приведённом уравнению

Ах, уравнения, квадратные,

вы такие разные и корней у вас

количество разное – от двух корней

до пустого множества.

Квадратные уравнения – это математическая модель, которая позволят передать особенности изучаемого явления, ситуации.

Математическая модель — приближённое описание какого-либо класса явлений внешнего мира, выраженное с помощью математической символики. Математ и ческая мод е ль — мощный метод познания внешнего мира, а также прогнозирования и управления.

Квадратные уравнения – это фундамент, на котором покоится величественное здание алгебры. Квадратные уравнения находят широкое применение при решении многих текстовых задач, при решении неравенств второй степени и дробно- рациональных, при решении биквадратных, тригонометрических, показательных, иррациональных уравнений. Решение многих задач физики сводится к решению алгебраических и квадратных уравнений.

В школьном курсе математики изучаются формулы корней квадратных уравнений, с помощью которых можно решать любые квадратные уравнения.

Однако имеются и другие приёмы решения квадратных уравнений, которые позволяют очень быстро и рационально решать квадратные уравнения.

Данные приёмы решения заслуживают внимания, поскольку они не отражены в школьных учебниках математики.

Овладение данными приёмами поможет мне экономить время и эффективно решать уравнения. Потребность в быстром решении обусловлена применением тестовой системы итоговых экзаменов в 9 и 11 классах.

Я провела опрос старшеклассников:

Умеете вы решать квадратное уравнение?

8-б да! недавно изучали, 100%

Где применяются решения квадратных уравнений?

8-б – при решении задач из учебника.

9-б – при решении текстовых задач; при нахождении нулей квадратичной функции; при разложении квадратного трёхчлена на множители;

при решении квадратных неравенств;

при решении биквадратных уравнений;

при решении алгебраических уравнений, сводящихся к квадратным.

11-а – очень часто на уроках математики — при решении тригонометрических, показательных, логарифмических, иррациональных уравнений и неравенств;

при исследовании функций с помощью производной;

при нахождении пределов интегрирования;

на уроках физики.

Используешь ли ты при решении уравнений свойства коэффициентов?

Знакомясь с содержанием и структурой диагностических тестов ГИА, я подсчитала, что в среднем 23% всех заданий требуют умения решать квадратные уравнения.

Поэтому меня и заинтересовала эта тема.

1. Познакомиться с историей возникновения квадратных уравнений

2. Рассмотреть способы решения квадратных уравнений: метод выделения полного квадрата, решение квадратных уравнений по формуле, теорема Виета.

3.Изучить приёмы устного решения квадратного уравнения.

4.Узнать на уроках каких предметов задачи решаются с помощью квадратных уравнений.

5. Изучить структуру и содержание КИМ ГИА.

Гипотеза: знания различных способов решения квадратных уравнений и приёмов устного решения квадратных уравнений способствует быстрому и правильному решению задач и экономит время.

Задачи: Квадратные уравнения – это математическая модель реальности и её применение в школьном образовании.

Глава 1. История квадратных уравнений.

Квадратные уравнения в Древнем Вавилоне.

Необходимость решать уравнения не только первой, но и второй степени ещё в древности была вызвана потребность решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики. Квадратные уравнения умели решать около 2000 лет назад до н. э. вавилоняне. Применяя современную алгебраическую запись, можно сказать, что в их клинописных текстах встречаются, кроме неполных, и такие, например, полные квадратные уравнения:

Правило решения этих уравнений, изложено в вавилонских текстах, совпадает по существу с современным, однако неизвестно, каким образом дошли вавилоняне до этого правила. Почти все найденные до сих пор клинописные тексты переводят только задачи с решениями, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены.

Несмотря на высокий уровень развития алгебры в Вавилоне, в клинописных текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений.

Как составлял и решал Диофант квадратные уравнения.

В “Арифметике” Диофант нет систематического изложения алгебры, однако в ней содержится систематизированный ряд задач, сопровождаемых объяснениями и решаемых при помощи составления уравнений разных степеней.

При составлении уравнений Диофант для упрощения решения умело выбирает неизвестные.

Вот, к примеру, одна из его задач.

Задача 11. “Найти два числа, зная, что их сумма равна 20, а произведение – 96” .

Диофант рассуждает следующим образом: из условия задачи вытекает, что искомые числа не равны, так если бы они были равны, то их произведение равнялось бы не 96, а 100. Таким образом, одно из них будет больше половины их суммы, т. е. 10 – x. Разность между ними 2x. Отсюда уравнение

(10 + x) (10 – x) = 96,

Отсюда x = 2. Одно из искомых чисел равно 12, другое 8. Решение x = -2 для Диофанта не существует, так как греческая математика знала только положительные числа.

Если мы решим эту задачу, выбирая в качестве неизвестного одно из искомых чисел, то мы придем к решению уравнения.

y² – 20y + 96 = 0 (2)

Ясно, что, выбирая в качестве неизвестного полуразность искомых чисел, Диофант упрощает решение; ему удаётся свести задачу к решению не полного квадратного уравнения(1).

Квадратные уравнения в Индии

Задачи на квадратные уравнения встречаются уже в 499г. В Древней Индии были распространены публичные соревнования в решении трудных задач. В одной из старинных индийских книг говорится по поводу таких соревнований следующее:

« Как солнце блеском своим затмевает звёзды, так ученый человек затмит славу другого в народных собраниях, предлагая и решая алгебраические задачи».

Одна из задач знаменитого индийского математика XIIв. Бхаскары:

Решение Бхаскары свидетельствует о том, что он знал о двузначности корней квадратных уравнений. Часть страницы из алгебры Бхаскары (вычисление корней).

Квадратные уравнения у ал-Хорезми

В алгебраическом трактате ал-Хорезми даётся классификация линейных уравнений и квадратных уравнений. Автор насчитывает 6 видов уравнений, выражая их следующим образом:

1) “Квадраты равны корнями”, т. е. ax² = bx.

2) “Квадраты равны числу”, т. е. ax²= c.

3) “Корни равны числу”, т. е. ax = c

4) “Квадраты и числа равны корням”, т. е. ax² + c = bx/

5) “Квадраты и корни равны числу”, т. е. ax² + bx = c.

6) “Корни и числа равны квадратам”, т. е. bx + c + ax²

Для ал-Хорезми, избегавшего употребления отрицательных чисел, члены каждого из этих уравнений слагаемые, а не вычитаемые. При этом заведомо не берутся во внимание уравнения, у которых нет положительных решений. Автор излагает способы решения указанных уравнений, пользуясь приёмами ал-джабар и ал-мукабала. Его решения, конечно, не совпадает полностью с нашим. Уже не говоря о том, что оно чисто риторическое, следует отметить, например, что при решении неполного квадратного уравнения первого вида ал-Хорезми, как и все математики до 17 века, не учитывает нулевого решения, вероятно, потому, что в конкретных практических задачах оно не имеет значения. При решении полных квадратных уравнений ал-Хорезми на частных числовых примерах излагает правила решения, а затем их геометрические доказательства.

Квадратные уравнения в Европе XIII — XVIIв.в.

Формулы решения квадратных уравнений по образцу ал-Хорезми в Европе были впервые изложены в книге “Книге абака”, написанной в 1202 г. Итальянским математиком Леонардо Фибоначчи. Этот объёмистый труд, в котором отражено влияние математики как стран ислама, так и Древней Греции, отличается и полнотой, и ясностью изложения. Автор разработал самостоятельно некоторые новые алгебраические примеры задач и первый в Европе подошёл к введению отрицательных чисел. Его книга способствовала распространению алгебраических знаний не только в Италии, но и в Германии, Франции и других стран Европы. Многие задачи из “Книги абака” переходили почти во все европейские учебники 16 – 17 веков и частично 18 века. Общее правило решения квадратных уравнений, приведённых к единому каноническому виду: x² + bx = c,

при всевозможных комбинациях знаков коэффициентов b, c было сформулировано в Европе лишь в 1544 г. М.Штифелем.

Вывод формулы решения квадратного уравнения в общем виде имеется у Виета, однако Виет признавал только положительные корни. Итальянские математики Тарталья, Кардано, Бомбелли среди первых в 16 веке учитывают, помимо положительных, и отрицательные корни. Лишь в 17 веке благодаря трудам Жирара, Декарта, Ньютона и других учёных способов решения квадратных уравнений принимает современный вид.

Квадратные уравнения – это математическая модель, которая позволят передать особенности изучаемого явления, реальной ситуации.

2.1 Квадратные уравнения и его корни

Квадратным уравнением называется уравнение ах² + bх + с = 0, где а≠0, а, b,с – заданные числа числа, х – неизвестное.

Коэффициенты а, b,с квадратного уравнения называют так: а- первым или старшим коэффициентом, b-вторым коэффициентом, с-свободным членом.

Неполное квадратное уравнение

Квадратное уравнение ах² + bх + с = 0 называют неполным , если хотя бы один из коэффициентов b или с равен нулю.

2) ах² + с = 0, ах² = -с

1. если с>0 , то нет действительных корней

2. если с , то х²= -с/а

2.2 Метод выделения полного квадрата

Пример1: решить квадратное уравнение

Преобразуем это уравнение так:

Следовательно, х+1=2 или х+1= -2, откуда х1=1, х2= -3.

Решая уравнение, мы преобразовали его так, что в левой части получился квадрат двучлена, а правая часть не содержит неизвестное.

2.3 Решение квадратных уравнений по формуле.

Если D , то уравнение не имеет действительных корней

Пример1: х² — 4х +5 =0

D , то уравнение не имеет действительных корней

Пример2: 2х² + 3х + 1 = 0

«Виет – творец математической формулы.»

«Французский геометр Виет был выше всех своих современников. Он прославился обобщением алгебры и сделал несколько важных открытий в этой отрасли человеческих знаний.»

Решение уравнений с использованием теоремы Виета.

Как известно, приведенное квадратное уравнение имеет вид

х 2 + px + c = 0. (1)

Его корни удовлетворяют теореме Виета, которая при а =1 имеет вид

x 1 x 2 = q,

Т.е., сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.

Отсюда можно сделать следующие выводы (по коэффициентам p и q можно предсказать знаки корней).

а) Если сводный член q приведенного уравнения (1) положителен ( q > 0 ), то уравнение имеет два одинаковых по знаку корня и это зависти от второго коэффициента p . Если р , то оба корня отрицательны, если р , то оба корня положительны.

x 2 – 3x + 2 = 0; x 1 = 2 и x 2 = 1, так как q = 2 > 0 и p = — 3

x 2 + 8x + 7 = 0; x 1 = — 7 и x 2 = — 1, так как q = 7 > 0 и p= 8 > 0.

б) Если свободный член q приведенного уравнения (1) отрицателен ( q ), то уравнение имеет два различных по знаку корня, причем больший по модулю корень будет положителен, если p , или отрицателен, если p > 0 .

x 2 + 4x – 5 = 0; x 1 = — 5 и x 2 = 1, так как q= — 5 и p = 4 > 0;

x 2 – 8x – 9 = 0; x 1 = 9 и x 2 = — 1, так как q = — 9 и p = — 8

Пример1: х² — 14х – 15 =0

Теорема Виета для полного квадратного уравнения:

По праву достойна в стихах быть воспета

О свойствах корней теорема Виета.

Что лучше, скажи, постоянства такого:

Умножишь ты корни – и дробь уж готова?

В числителе с, в знаменателе а.

А сумма корней тоже дроби равна.

Хоть с минусом дробь, что за беда.

В числителе в, b знаменателе а.

2.5 Биквадратные уравнения.

Биквадратным уравнением — называется уравнение вида ax 4 + bx 2 + c = 0 .

Биквадратное уравнение приводится к квадратному уравнению при помощи подстановки .

Новое квадратное уравнение относительно переменной :

Решая это уравнение, мы получаем корни квадратного уравнения и . Решая эти два уравнения ( и ) относительно переменной , мы получаем корни данного биквадратного уравнения.

Алгоритм решения биквадратных уравнений :

Ввести новую переменную
Подставить данную переменную в исходное уравнение
Решить квадратное уравнение относительно новой переменной
После нахождения корней ( ) подставить их в нашу переменную и найти исходные корни биквадратного уравнения

Решим биквадратное уравнение . Сначала приводим это уравнение к квадратному. Для этого введем вспомогательное неизвестное такое, что . Тогда . Теперь данное биквадратное уравнение приводится к виду:

Решая это квадратное уравнение, мы получим , . Так как , то данное биквадратное уравнение эквивалентно системе двух уравнений:

Решим каждое из этих уравнений и найдем объединение множеств их решений.

Глава 3. Приёмы устного решения квадратного уравнения.

Свойства коэффициентов квадратного уравнения:

Пусть дано квадратное уравнение ах 2 + bх + с = 0, где а ≠ 0.

1) Если, а + b + с = 0 (т.е. сумма коэффициентов равна нулю), то х 1 = 1,

Доказательство: Разделим обе части уравнения на а ≠ 0, получим приведенное квадратное уравнение

x 2 + b/a • x + c/a = 0.

Согласно теореме Виета

По условию а – b + с = 0, откуда b = а + с. Таким образом,

x 1 + x 2 = — а + b/a= -1 – c/a,

x 1 x 2 = — 1• ( — c/a),

т.е. х 1 = -1 и х 2 = c/a, что и требовалось доказать.

1)Решим уравнение 345х 2 – 137х – 208 = 0.

Решение. Так как, а + b + с = 0 (345 – 137 – 208 = 0), то

х 1 = 1, х 2 = c/a = -208/345.

2)Решим уравнение 132х 2 – 247х + 115 = 0.

Решение. Так как, а + b + с = 0 (132 – 247 + 115 = 0), то

х 1 = 1, х 2 = c/a = 115/132.

3)Решим уравнение 5х 2 – 8х + 3 = 0.

Решение. Так как 5 – 8 + 3 = 0, то х 1 = 1; х 2 = 0,6.

Если в квадратном уравнении ах² + bх + с = 0 выполняется равенство а + с = в, то х1 = -1; х2 = — с/а.

1) 5х 2 – 8х + 3 = 0.

Так как 5 – 8 + 3 = 0, то х 1 = 1; х 2 = 0,6.

2) Решить уравнения с большими коэффициентами :

1) 319х² + 1988x + 1669 = 0.

х 1 = — 1; х 2 = -1669/319.

2) 839х² – 448x – 391 = 0.

х 1 = 1; х 2 = -391/839.

3) 939х² + 978x + 39 = 0.

х 1 = — 1; х 2 = -39/939.

3.2 Приём «Переброски»

Рассмотрим квадратное уравнение

ах 2 + bх + с = 0, где а ≠ 0.

Умножая обе его части на а, получаем уравнение

а 2 х 2 + аbх + ас = 0.

Пусть ах = у , откуда х = у/а ; тогда приходим к уравнению

равносильно данному. Его корни у 1 и у 2 найдем с помощью теоремы Виета.

Окончательно получаем х 1 = у 1 /а и х 1 = у 2 /а . При этом способе коэффициент а умножается на свободный член, как бы «перебрасывается» к нему, поэтому его называют способом «переброски» . Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.

1) Решим уравнение 2х 2 – 11х + 15 = 0.

Решение . «Перебросим» коэффициент 2 к свободному члену, в результате получим уравнение

у 2 – 11у + 30 = 0.

Согласно теореме Виета:

у 1 = 5 х 1 = 5/2 x 1 = 2,5

у 2 = 6 x 2 = 6/2 x 2 = 3.

2) Решим уравнение 6х² — 7х – 3 = 0

Глава 4. Квадратные уравнения в предметах естественно-математического цикла .

Задача 1. Вертикально вверх с начальной скоростью 7 м/с брошен камень. Через некоторое время =0,41 с после этого брошен вертикально вверх другой камень с такой же скоростью. На какой высоте (от земли ) встретятся камни?

Решение: Необходимо составить уравнения движения для обоих тел. После чего объединить их и решить. Движение равноускоренное вдоль прямой, поэтому векторы не нужны и сразу пишем уравнения движения в скалярной форме. Ось координат направим вверх, тогда для скорости

V1 = V01 — g * t (поскольку начальная скорость направлена против силы тяжести.)

откуда для координаты

Х1 = Х01 + V01 * t — g * t * t / 2

для второго тела выпущенного в момент времени t1 = t + dt уравнение движения будет иметь вид

Х2 = Х02 + V02 * (t + dt) — g * (t + dt) * (t + dt) / 2

При встрече тел их координаты совпадут, что на языке математики запишется как

Х01 + V01 * t — g * t * t / 2 = Х02 + V02 * (t + dt) — g * (t + dt) * (t + dt) / 2

поскольку тела запускаются из одной и той же точки и с одной и той же скоростью, то

Х01 = Х02 и V01 = V02

и окончательно уравнение принимает вид

V0 * t — g * t * t / 2 = V0 * (t + dt) — g * (t + dt) * (t + dt) / 2

У полученного квадратного уравнения относительно t может быть два, одно или ни одного решения. Нас будут интересовать решения с t > 0. Решения с t

Задача 2. Груз свободно падает с высоты 500 метров. Какое расстояние преодолевает груз за последнюю секунду своего падения?

Решение: Потенциальная энергия переходит в кинетическую

v = корень квадратный(2*g*h) — это скорость в момент удара

Рассмотрим обратный процесс примем скорость v за начальную при движении вверх, тогда пройденный путь s=v*t-g*t^2/2.

Так как t=1, то s=v-g/2 = корень квадратный(2*g*h) -g/2 = 100-5=95 метров

Задача 3. Ускорение свободного падения на Земле равно 10 м/с. Какой продолжительности должны быть сутки, чтобы тела на экваторе были невесомы?

Решение: Центростремительное ускорение есть v^2/R и оно же должно равняться ускорению свободного падения g

отсюда следует, что линейная скорость точки на экваторе должна быть

далее определяем время, которое необходимо на один оборот с такой скоростью

переводим в минуты и часы и получаем, что это 1 час, 23 минуты и 37.9 секунды

Глава 5. Комплексные числа.

Решение многих задач физики и техники приводит к квадратным уравнениям с отрицательным дискриминантом. Эти уравнения не имеют решения в области действительных чисел. Но решение многих таких задач имеет вполне определенный физический смысл. Значение величин, получающихся в результате решения указанных уравнений, назвали комплексными числами.

Комплексные числа широко использовал отец русской авиации Н. Е. Жуковский (1847 – 1921) при разработке теории крыла, автором которой он является.

Комплексные числа и функции от комплексного переменного находят применение во многих вопросах науки и техники.

Но это совсем отдельный вопрос, он меня заинтересовал и может быть в 10 классе я познакомлюсь с этим числами и узнаю как решать квадратные уравнения с отрицательным дискриминантом.

Приобретать знания – храбрость,

Приумножать их – мудрость.

А умело применять — великое искусство!

В данной работе рассмотрена математическая модель — квадратное уравнение – которая позволят передать особенности изучаемого явления, реальной ситуации и решить её.

Рассмотрены виды уравнений, приёмы решения квадратных уравнений, которые позволяют очень быстро и рационально решать квадратные уравнения.

Данные приёмы решения заслуживают внимания, поскольку они не отражены в школьных учебниках математики. Овладение данными приёмами поможет мне экономить время и эффективно решать уравнения. Потребность в быстром решении обусловлена применением тестовой системы итоговых экзаменов в 9 и 11 классах.

Эта тема важна тем, что в результате ее изучения мы овладеете новым математическим аппаратом решения уравнений, позволяющим решать многообразные задачи не только математические, с помощью квадратных уравнений решаются текстовые задачи различных видов, находятся корни квадратного трехчлена, нули квадратичной функции (9 кл.), нахождение критических точек функции при исследовании функций, решение показательных, тригонометрических, логарифмических уравнений, приводимых к квадратным, нахождении пределов интегрирования(11кл.) Квадратные уравнения используются в курсе физики при решении задач по теме: «Равноускоренное движение», Падение тел» и других.

Научившийся решать квадратные уравнения со школьной скамьи (8 класс), знания могут пригодиться нам на протяжении всей жизни.

Я узнала , что квадратные уравнения с отрицательным дискриминантом решаются, но на не знакомом мне множестве чисел: на множестве комплексных чисел. Надеюсь что в старших классах узнаю об этом множестве чисел.

Задачи и цель, которые ставила в работе – знакомство с возникновение квадратных уравнений, рассмотрением различных способов решения квадратных уравнений, изучение приёмов устного решения квадратного уравнения, расширение знаний о применении квадратных уравнений в школьном образовании- достигнуты.

Работать было интересно, потому что я владела хорошими знаниями и навыками решения квадратных уравнений, узнала, что мои знания будут в дальнейшем востребованы на уроках математики и физики.

А Людмила Ивановна ещё считает, что отдельные главы моей работы могут быть использованы учителями математики при проведении элективного курса, дополнительной информацией при подготовке к уроку.

Ш. А. Алимов, Ю. М. Колягин, Ю. В. Сидоров, Н. Е. Федорова, М. И. Шабунин. Учебник 8 класса по алгебре.- М.: Просвещение, 2004.
И. С. Петраков. Математические кружки в 8-10 классах.- М.: Просвещение, 1987.
А. П. Савин. Энциклопедический словарь юного математика.- М.: Педагогика, 1989.
Г.И. Глейзер «История математики в школе»,- М.: Просвещение,1982.

элементов содержания по МАТЕМАТИКЕ для составления

контрольных измерительных материалов для проведения

в 2012 году единого государственного экзамена

Квадратные уравнения
Квадратные неравенства
Квадратичная функция, ее график

Задачи, решаемые с помощью квадратных уравнений на ЕГЭ

Из пункта А в пункт В, расстояние между которыми 40 км, одновременно выехали автомобилист и велосипедист. Известно, что в час автомобилист проезжает на 45 км больше, чем велосипедист.

Определите скорость велосипедиста, если известно, что он прибыл в пункт В на 2 часа позже автомобилиста.

Ответ дайте в км/ч.

Из пункта А в пункт В, расстояние между которыми 60 км, одновременно выехали автомобилист и велосипедист. Известно, что в час автомобилист проезжает на 45 км больше, чем велосипедист

Определите скорость велосипедиста, если известно, что он прибыл в пункт В на 3 часа позже автомобилиста. Ответ дайте в км/ч.

Из пункта А в пункт В, расстояние между которыми 30 км, одновременно выехали автомобилист и велосипедист. Известно, что в час автомобилист проезжает на 25 км больше, чем велосипедист.

Определите скорость велосипедиста, если известно, что он прибыл в пункт В на 50 минут

позже автомобилиста. Ответ дайте в км/ч.

Прямая параллельна касательной к графику функции . Найдите абсциссу точки касания

Найдите наибольшее значение функции y = log 1/2 ( x 2 + 4 x + 8)

Найдите наибольшее значение функции на отрезке

y = ( x + 1)2( x − 3) − 2[−2; 0]

7 2х = 6·7 х + 5 = 0

Решите уравнение .
Найдите наименьший корень уравнения .
Решите уравнение:
Решите уравнение .
Найдите сумму корней уравнения на промежутке [- π ;2 π ].

Решите уравнение 6cos2 x − 7cos x − 5 = 0 .Укажите корни принадлежащие отрезку [− π ; 2 π ]
Вычислите площадь фигуры, ограниченной линиями:

Вычислите площадь фигуры, ограниченной линиями :

Найдите тангенс угла наклона касательной к графику функции в точке с абсциссой .

Укажите промежуток, на котором функция только возрастает .
Найдите точку минимума функции .

Найдите наибольшее значение функции на отрезке .

Задачи с физическим содержанием, решаемые с помощью квадратных уравнений на ЕГЭ

Камень брошен вертикально вверх. Пока камень не упал, высота, на которой он находится, описывается формулой h ( t ) = −5 t ² +18 t , где h – высота в метрах, t – время в секундах, прошедшее с момента броска.

Сколько секунд камень находился на высоте не менее 9 метров.

В боковой стенке высокого цилиндрического бака у самого дна закреплен кран.

После его открытия вода начинает вытекать из бака, при этом высота столба воды в нем, выраженная в метрах, меняется по закону H ( t )= H 0 — √2 gH 0 kt + g,/2к²t² где — время в секундах, прошедшее с момента открытия крана, начальная высота столба H 0 = 5 м, k = 1/700

отношение площадей поперечных сечений крана и бака, ускорение свободного падения (считайте g = 10 м / с²) .Через сколько секунд после открытия крана в баке

останется четверть первоначального объема воды?

В боковой стенке высокого цилиндрического бака у самого дна закреплен кран.

останется четверть первоначального объема воды?

Расстояние от наблюдателя, находящегося на небольшой высоте h километров над землей, до наблюдаемой им линии горизонта вычисляется по формуле L=√2RH , где R (км) — радиус Земли R = 6400 .C какой высоты горизонт виден на расстоянии 32 километра? Ответ выразите в километрах .

Высоту над землёй подброшенного вверх мяча можно вычислить по формуле h(t) = 1 + 11t – 5t² (h— высота в метрах, t — время в секундах, прошедшее с момента броска). Сколько секунд мяч будет находиться на высоте более 3 метров?

Зависимость объёма спроса q (единиц в месяц) на продукцию предприятия-монополиста

от цены p . (тыс. руб.) задается формулой q = 55 − 5 p r.

Выручка предприятия за месяц r (в тыс. руб.) вычисляется

по формуле r ( p ) = q p . ⋅

Определите наибольшую цену р, при которой месячная выручка r ( p ) составит 140 тыс. руб

Видео:Квадратные уравнения от «А» до «Я». Классификация, решение и теорема Виета | МатематикаСкачать

Курсовая работа: Формирование умения решения квадратных уравнений в 8 классе

ГОУ СПО «Кунгурское педагогическое училище»

Формирование умения решения квадратных уравнений в 8 классе

Видео:Формула корней квадратного уравнения. Алгебра, 8 классСкачать

Курсовая работа

по методике математики

Глава 1. Теоретические аспекты обучению решения уравнений в 8 классе

1.1. Из истории возникновения квадратных уравнений 6

1.2. Основные направления изучения линий уравнений в школьном курсе алгебры 12

1.3. Методика изучения квадратных уравнений 15

Глава 2. Методико-педагогические основы обучения решению квадратных уравнений

2.1. Урок – лекция по теме «Формула корней квадратного уравнения с четным вторым коэффициентом» 23

2.2. Урок – практикум по теме «Квадратные уравнения» 28

2.3. Обобщающий урок по теме «Квадратные уравнения» в форме игры «Звездный час» 32

Список литературы 38

Сухие строки уравнений –

В них сила разума влилась.

В них объяснение явлений,

Вещей разгаданная связь.

Уравнения в школьном курсе алгебры занимают ведущее место. На их изучение отводится времени больше, чем на любую другую тему школьного курса математики. Сила теории уравнений в том, что она не только имеет теоретическое значение для познания естественных законов, но и служит конкретным практическим целям. Большинство задач о пространственных формах и количественных отношениях реального мира сводится к решению различных видов уравнений. Овладевая способами их решения, люди находят ответы на различные вопросы из науки и техники (транспорт, сельское хозяйство, промышленность, связь и т. д.). Так же для формирования умения решать уравнения большое значение имеет самостоятельная работа учащегося при обучении решения уравнений. При изучении любой темы уравнения могут быть использованы как эффективное средство закрепления, углубления, повторения и расширения теоретических знаний, для развития творческой математической деятельности учащихся.[10,241].

Автором данной работы выбрана тема «Формирование умения решения квадратных уравнений в 8 классе», так как она актуальна в современном мире; это объясняется тем, что уравнения широко используются в различных разделах математики, в решении важных прикладных задач.

Для этой темы характерна большая глубина изложения и богатство устанавливаемых с ее помощью связей в обучении, логическая обоснованность изложения. Поэтому она занимает исключительное положение в линии уравнений. К изучению темы «Квадратные уравнения» учащиеся приступают, уже накопив определенный опыт, владея достаточно большим запасом алгебраических и общематематических представлений, понятий, умений. В значительной мере именно на материале данной темы осуществляется синтез материала, относящегося к уравнениям.

Исходя из вышесказанного, автор, выбирая тему курсовой работы, руководствовался ее значимостью и сложностью при обучении учащихся решению квадратных уравнений разного вида.

Цель работы: формирование представлений о работе над квадратными уравнениями на уроках математики. Исходя из данной цели, были поставлены следующие задачи:

· изучить научно-методическую литературу, касающуюся изучению уравнений;

· проанализировать школьные учебники и выделить в них место уравнений.

· разработать уроки по данной теме.

Для решения вышеуказанных задач были изучены следующие литературные источники:

1) Алгебра: Учеб. для 8 кл. общеобразоват. учреждений / С.М. Никольский, М.К. Потапов и др. – 2-е изд. – М.: Просвещение, 2003. – 287 с.

2) Алгебра: Учеб. для 8 кл. общеобразоват. учреждений / Ш.А.Алимов, Ю.М.Колягин, Ю.В.Сидоров и др. – 10-е изд. – М.: Просвещение, 2003. – 255с.

3) Мордкович А.Г.. Алгебра: учеб. для 8 кл. общеобразоват. учреждений. – М.: Просвещение, 2004. – 287с.

4) Бекаревич А.Б. Уравнения в школьном курсе математики. – М., 2000. – 241с.

5) Глейзер Г.И. История математики в школе VII – VIII классы. – М., 1982.

6) Колягин Ю.М. Методика преподавания математике в средней школе. Частные методики. – М.: Просвещение, 2002.

7) Маркушевич Л.А. Уравнения и неравенства в заключительном повторении курса алгебры средней школы // Математика в школе. – 2001. — №1. – с.15

8) Методика и технология обучения математике. Курс лекций: пособие для вузов / под ред. Н.Л.Стефановой, Н.С. Подходовой. – М.: Дрофа, 2005. – 416 с.

9) Мишин В.И. Методика преподавания математики в средней школе. – М.,1999.- 398с.

10) Оганесян В.А. Методика преподавания математики в средней школе. – М.: Просвещение, 2003. – 368 с.

Проанализировав некоторые источники, можно сделать вывод о недостаточном освещении изучаемого вопроса в современной методической литературе.

Объект исследования работы: процесс обучения математике.

Предмет: формирование умения решения квадратных уравнений у учащихся 8-го класса.

Контингент: учащиеся 8-го класса.

Глава 1. Теоретические аспекты обучению решения уравнений в 8 классе

1.1. Из истории возникновения квадратных уравнений

Алгебра возникла в связи с решением разнообразных задач при помощи уравнений. Обычно в задачах требуется найти одну или несколько неизвестных, зная при этом результаты некоторых действий, произведенных над искомыми и данными величинами. Такие задачи сводятся к решению одного или системы нескольких уравнений, к нахождению искомых с помощью алгебраических действий над данными величинами. В алгебре изучаются общие свойства действий над величинами.

Некоторые алгебраические приемы решения линейных и квадратных уравнений были известны еще 4000 лет назад в Древнем Вавилоне.

Квадратные уравнения в Древнем Вавилоне

Необходимость решать уравнения не только первой, но и второй степени еще в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики. Квадратные уравнения умели решать около 2000 лет до нашей эры вавилоняне. Применяя современную алгебраическую запись, можно сказать, что в их клинописных текстах встречаются, кроме неполных, и такие, например, полные квадратные уравнения:

Правило решения этих уравнений, изложенное в вавилонских текстах, совпадает по существу с современным, однако неизвестно, каким образом дошли вавилоняне до этого правила. Почти все найденные до сих пор клинописные тексты приводят только задачи с решениями, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены. Несмотря на высокий уровень развития алгебры в Вавилоне, в клинописных текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений.

В «Арифметике» Диофанта нет систематического изложения алгебры, однако в ней содержится систематизированный ряд задач, сопровождаемых объяснениями и решаемых при помощи составления уравнений разных степеней.

При составлении уравнений Диофант для упрощения решения умело выбирает неизвестные.

Вот, к примеру, одна из его задач.

Задача 2. «Найти два числа, зная, что их сумма равна 20, а произведение — 96».

Диофант рассуждает следующим образом: из условия задачи вытекает, что искомые числа не равны, так как если бы они были равны, то их произведение равнялось бы не 96, а 100. Таким образом, одно из них будет больше половины их суммы, т. е. 10 + х. Другое же меньше, т. е. 10 — х. Разность между ними 2х. Отсюда уравнение:

Отсюда х = 2. Одно из искомых чисел равно 12, другое 8. Решение х = — 2 для Диофанта не существует, так как греческая математика знала только положительные числа.

Если решить эту задачу, выбирая в качестве неизвестного одно из искомых чисел, то можно прийти к решению уравнения:

Ясно, что, выбирая в качестве неизвестного полуразность искомых чисел, Диофант упрощает решение; ему удается свести задачу к решению неполного квадратного уравнения.

Квадратные уравнения в Индии

Задачи на квадратные уравнения встречаются уже в астрономическом трактате «Ариабхаттиам», составленном в 499 г. индийским математиком и астрономом Ариабхаттой. Другой индийский ученый, Брахмагупта (VII в.), изложил общее правило решения квадратных уравнений, приведенных к единой канонической форме:

ax 2 + bх = с, а> 0. (1)

В уравнении (1) коэффициенты, могут быть и отрицательными. Правило Брахмагупты по существу совпадает с нашим.

В Индии были распространены публичные соревнования в решении трудных задач. В одной из старинных индийских книг говорится по поводу таких соревнований следующее: «Как солнце блеском своим затмевает звезды, так ученый человек затмит славу в народных собраниях, предлагая и решая алгебраические задачи». Задачи часто облекались в стихотворную форму.

Вот одна из задач знаменитого индийского математика XII в. Бхаскары.

Название: Формирование умения решения квадратных уравнений в 8 классе
Раздел: Рефераты по математике
Тип: курсовая работа Добавлен 00:03:11 03 июля 2008 Похожие работы
Просмотров: 3447 Комментариев: 21 Оценило: 3 человек Средний балл: 5 Оценка: неизвестно Скачать

«Обезьянок резвых стая	А двенадцать по лианам
Всласть поевши, развлекалась	Стали прыгать, повисая
Их в квадрате часть восьмая	Сколько ж было обезьянок,
На поляне забавлялась	Ты скажи мне, в этой стае?»

Решение Бхаскары свидетельствует о том, что автор знал о двузначности корней квадратных уравнений.

Соответствующее задаче 3 уравнение:

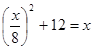
Бхаскара пишет под видом:

x 2 — 64x = — 768

и, чтобы дополнить левую часть этого уравнения до квадрата, прибавляет к обеим частям 32 2 , получая затем:

x 2 — б4х + 32 2 = -768 + 1024,

Квадратные уравнения у Аль-Хорезми

В алгебраическом трактате Аль-Хорезми дается классификация линейных и квадратных уравнений. Автор насчитывает 6 видов уравнений, выражая их следующим образом:

1) «Квадраты равны корням», т. е. ах 2 = bх.

2) «Квадраты равны числу», т. е. ах 2 = с.

3) «Корни равны числу», т. е. ах = с.

4) «Квадраты и числа равны корням», т. е. ах 2 + с = bх.

5) «Квадраты и корни равны числу», т. е. ах 2 + bх =с.

6) «Корни и числа равны квадратам», т. е. bх + с == ах 2 .

Для Аль-Хорезми, избегавшего употребления отрицательных чисел, члены каждого из этих уравнений слагаемые, а не вычитаемые. При этом заведомо не берутся во внимание уравнения, у которых нет положительных решений. Автор излагает способы решения указанных уравнений, пользуясь приемами ал-джабр и ал-мукабала. Его решение, конечно, не совпадает полностью с нашим. Уже не говоря о том, что оно чисто риторическое, следует отметить, например, что при решении неполного квадратного уравнения первого вида Аль-Хорезми, как и все математики до XVII в., не учитывает нулевого решения, вероятно, потому, что в конкретных практических задачах оно не имеет значения. При решении полных квадратных уравнений Аль-Хорезми на частных числовых примерах излагает правила решения, а затем их геометрические доказательства.

Задача 4. «Квадрат и число 21 равны 10 корням. Найти корень» (подразумевается корень уравнения х 2 + 21 = 10х).

Решение: раздели пополам число корней, получишь 5, умножь 5 само на себя, от произведения отними 21, останется 4. Извлеки корень из 4, получишь 2. Отними 2 от 5, получишь 3, это и будет искомый корень. Или же прибавь 2 к 5, что даст 7, это тоже есть корень.

Трактат Аль-Хорезми является первой, дошедшей до нас книгой, в которой систематически изложена классификация квадратных уравнений и даны формулы их решения.[3,75]

Квадратные уравнения в Европе XII — XVII в.

Формы решения квадратных уравнений по образцу Аль-Хорезми в Европе были впервые изложены в «Книге абака», написанной в 1202г. итальянским математиком Леонардом Фибоначчи. Автор разработал самостоятельно некоторые новые алгебраические примеры решения задач и первый в Европе подошел к введению отрицательных чисел.

Эта книга способствовала распространению алгебраических знаний не только в Италии, но и в Германии, Франции и других странах Европы. Многие задачи из этой книги переходили почти во все европейские учебники XIV-XVII вв. Общее правило решения квадратных уравнений, приведенных к единому каноническому виду x 2 + bх = с при всевозможных комбинациях знаков и коэффициентов b, c, было сформулировано в Европе в 1544 г. М.Штифелем.

Вывод формулы решения квадратного уравнения в общем виде имеется у Виета, однако Виет признавал только положительные корни. Итальянские математики Тарталья, Кардано, Бомбелли среди первых вXVI в. учитывают, помимо положительных, и отрицательные корни. Лишь в XVII в. благодаря трудам Жирара, Декарта, Ньютона и других ученых способ решения квадратных уравнений принимает современный вид.[5,12].

Истоки алгебраических методов решения практических задач связаны с наукой древнего мира. Как известно из истории математики, значительная часть задач математического характера, решаемых египетскими, шумерскими, вавилонскими писцами-вычислителями (XX—VI вв. до н. э.), имела расчетный характер. Однако уже тогда время от времени возникали задачи, в которых искомое значение величины задавалось некоторыми косвенными условиями, требующими, с нашей современной точки зрения, составления уравнения или системы уравнений. Первоначально для решения таких задач применялись арифметические методы. В дальнейшем начали формироваться начатки алгебраических представлений. Например, вавилонские вычислители умели решать задачи, сводящиеся с точки зрения современной классификации к уравнениям второй степени. Был создан метод решения текстовых задач, послуживший в дальнейшем основой для выделения алгебраического компонента и его независимого изучения.

Это изучение осуществлялось уже в другую эпоху сначала арабскими математиками (VI—Х вв. н. э.), выделившими характерные действия, посредством которых уравнения приводились к стандартному виду приведение подобных членов, перенос членов из одной части уравнения в другую с переменой знака. А затем европейскими математиками Возрождения, в итоге длительного поиска создавшими язык современной алгебры, использование букв, введение символов арифметических операций, скобок и т. д. На рубеже XVI—XVII вв. алгебра как специфическая часть математики, обладающая своим предметом, методом, областями приложения, была уже сформирована. Дальнейшее ее развитие, вплоть до нашего времени, состояло в совершенствовании методов, расширении области приложений, уточнении понятий и связей их с понятиями других разделов математики.

Итак, ввиду важности и обширности материала, связанного с понятием уравнения, его изучение в современной методике математики связано с тремя главными областями своего возникновения и функционирования.

1.2. Основные направления изучения линий уравнений в школьном курсе алгебры

Уравнение как общематематическое понятие многоаспектно. Можно выделить главные области возникновения и функционирования понятия «уравнение» как:

· средства решения текстовых задач;

· особого рода формулы, служащей в алгебре объектом изучения;

· формулы, которой косвенно определяются числа или координаты точек плоскости (пространства), служащие его решением.[12,268]

Каждое из этих представлений оказалось в том или ином отношении полезным.

Названным областям относятся три основных направления изучения линий уравнений в школьном курсе алгебры.

1. Прикладная направленность линии уравнений раскрывается главным образом при изучении алгебраического метода решения текстовых задач. Этот метод широко применяется в школьной математике, поскольку он связан с обучением приемам, используемым в приложениях математики.

В настоящее время, ведущее положение в приложениях математики занимает математическое моделирование (Математическое моделирование заключается в конструировании по определенным правилам некоторой формальной системы, которая отображает через совокупность математических операций над величинами определенную гипотезу о структуре или воспитания). Используя это понятие, можно сказать, что прикладное значение уравнений, их систем определяется тем, что они являются основной частью математических средств, используемых в математическом моделировании. [14,246].

2. Теоретико-математическая направленность линии уравнений раскрывается в двух аспектах:

· выделение и изучение наиболее важных классов уравнений, и их систем;

· изучение обобщенных понятий, относящихся ко всей линии в целом.

Оба эти аспекта необходимы в курсе школьной математики. Основные классы уравнений связаны с простейшими и одновременно наиболее важными математическими моделями. Использование обобщенных понятий и методов позволяет логически упорядочить изучение линии в целом, поскольку они описывают то общее, что имеется в процедурах и приемах решения, относящихся к отдельным классам уравнений, неравенств, систем. В свою очередь, эти общие понятия и методы опираются на основные логические понятия: неизвестное, равенство, равносильность, логическое следование, которые также должны быть раскрыты в линии уравнений.

3. Направленность на установление связей с остальным содержанием курса математики. Эта линия тесно связана с числовой линией, причем эта связь — двусторонняя. Основная идея, реализуемая в процессе установления взаимосвязи этих линий,— это идея последовательного расширения числовой системы. Все числовые области, рассматриваемые в школьной алгебре и началах анализа, за исключением области всех действительных чисел, возникают в связи с решением каких-либо уравнений.

Например, введение арифметического квадратного корня из рациональных чисел позволяет записывать корни не только уравнений вида х 2 = b, где b—неотрицательное рациональное число, но и любых квадратных уравнений с рациональными коэффициентами и неотрицательным дискриминантом.[9,341]

Линия уравнений тесно связана также и с функциональной линией. Одна из важнейших таких связей — приложения методов, разрабатываемых в линии уравнений, к исследованию функции (например, к заданиям на нахождение области определения некоторых функций, их корней, промежутков знакопостоянства и т. д.). С другой стороны, функциональная линия оказывает существенное влияние как на содержание линии уравнений , так и на стиль ее изучения. В частности, функциональные представления служат основой привлечения графической наглядности к решению и исследованию уравнений и их систем.[12,269]

Изучение и использование преобразований уравнений и их систем, с одной стороны, предполагают достаточно высокую логическую культуру учащихся, а с другой стороны, в процессе изучения и применения таких преобразований имеются широкие возможности для формирования логической культуры.

Таким образом, владение содержанием линии уравнений позволяет расширить список выполнимых преобразований. Так, умение решать квадратные уравнения позволяет осуществлять сокращение дробей, в числителе или знаменателе которых имеется квадратный трехчлен. В итоге изучения материала линии уравнений учащиеся должны не только овладеть применением алгоритмических предписаний к решению конкретных заданий, но и научиться использовать логические средства для обоснования решений в случаях, когда это необходимо.

1.3. Методика изучения квадратных уравнений

С началом изучения систематического курса алгебры основное внимание уделяется способам решения квадратных уравнений, которые становятся специальным объектом изучения. Для этой темы характерна большая глубина изложения и богатство устанавливаемых с ее помощью связей в обучении, логическая обоснованность изложения. Поэтому она занимает исключительное положение в линии уравнений и неравенств. К изучению этой темы учащиеся приступают, уже накопив определенный опыт, владея достаточно большим запасом алгебраических и общематематических представлений, понятий, умений.

Умение решать квадратные уравнения служит базой для решения других уравнений и их систем (дробных рациональных, иррациональных, высших степеней).

Для того чтобы решить любое квадратное уравнение, учащиеся должны знать:

· формулу нахождения дискриминанта;

· формулу нахождения корней квадратного уравнения;

· алгоритмы решения уравнений данного вида.

· решать неполные квадратные уравнения;

· решать полные квадратные уравнения;

· решать приведенные квадратные уравнения;

· находить ошибки в решенных уравнениях и исправлять их;

Решение каждого уравнения складывается из двух основных частей:

· преобразования данного уравнения к простейшим;

· решения уравнений по известным правилам, формулам или алгоритмам.

При изучении темы «Квадратные уравнения» рассматриваются неполные, полные и приведенные квадратные уравнения. Для изучения данной темы были проанализированы современные школьные учебники разных авторов, таких как А.Г.Мордкович, С.М.Никольский, Ю.Н.Макарычев, М.И.Башмаков.

Видео:Как решать квадратные уравнения. 8 класс. Вебинар | МатематикаСкачать

Как решать квадратные уравнения

О чем эта статья:

Видео:Алгебра 8. Урок 9 - Квадратные уравнения. Полные и неполныеСкачать

Понятие квадратного уравнения

Уравнение — это равенство, содержащее переменную, значение которой нужно найти.

Например, х + 8 = 12 — это уравнение, которое содержит переменную х.

Корень уравнения — это такое значение переменной, которое при подстановке в уравнение обращает его в верное числовое равенство.

Например, если х = 5, то при подстановке в уравнение мы получим 5 + 8 = 12. 13 = 12 — противоречие. Значит, х = 5 не является корнем уравнения.

А вот если х = 4, то при подстановке в уравнение мы получим 4 + 8 = 12. 12 = 12 — верное равенство. Значит, х = 4 является корнем уравнения.

Решить уравнение — значит найти все его корни или доказать, что их не существует.

Квадратное уравнение — это уравнение вида ax 2 + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.

Чтобы запомнить месторасположение коэффициентов, давайте потренируемся определять их.

Квадратные уравнения могут иметь два корня, один корень или не иметь корней.

Чтобы определить, сколько корней имеет уравнение, нужно обратить внимание на дискриминант. Чтобы его найти, берем формулу: D = b 2 − 4ac. А вот свойства дискриминанта:

если D 0, есть два различных корня.

С этим разобрались. А сейчас посмотрим подробнее на различные виды квадратных уравнений.

Разобраться в теме еще быстрее с помощью опытного преподавателя можно на курсах по математике в онлайн-школе Skysmart.

Видео:5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

Приведенные и неприведенные квадратные уравнения

Квадратное уравнение может быть приведенным или неприведенным — все зависит от от значения первого коэффициента.

Приведенное квадратное уравнение — это уравнение, где старший коэффициент, тот который стоит при одночлене высшей степени, равен единице.

Неприведенным называют квадратное уравнение, где старший коэффициент отличается от единицы.

Давайте-ка на примерах — вот у нас есть два уравнения:

x 2 — 2x + 6 = 0
x 2 — x — 1/4 = 0

В каждом из них старший коэффициент равен единице (которую мы мысленно представляем при x 2 ), а значит уравнение называется приведенным.

2x 2 − 4x — 12 = 0 — первый коэффициент отличен от единицы (2), значит это неприведенное квадратное уравнение.

Каждое неприведенное квадратное уравнение можно преобразовать в приведенное, если произвести равносильное преобразование — разделить обе его части на первый коэффициент.

Пример 1. Превратим неприведенное уравнение: 8x 2 + 20x — 9 = 0 — в приведенное.

Для этого разделим обе части исходного уравнения на старший коэффициент 8:

Ответ: равносильное данному приведенное уравнение x 2 + 2,5x — 1,125 = 0.

Видео:Квадратное уравнение. Как решить? | Математика ОГЭ 2023 | УмскулСкачать

Полные и неполные квадратные уравнения

В определении квадратного уравнения есть условие: a ≠ 0. Оно нужно, чтобы уравнение ax 2 + bx + c = 0 было именно квадратным. Если a = 0, то уравнение обретет вид линейного: bx + c = 0.

Что касается коэффициентов b и c, то они могут быть равны нулю, как по отдельности, так и вместе. В таком случае квадратное уравнение принято называть неполным.

Неполное квадратное уравнение —— это квадратное уравнение вида ax 2 + bx + c = 0, где оба или хотя бы один из коэффициентов b и c равен нулю.

Полное квадратное уравнение — это уравнение, у которого все коэффициенты отличны от нуля.

Для самых любопытных объясняем откуда появились такие названия:

Если b = 0, то квадратное уравнение принимает вид ax 2 + 0x+c=0 и оно равносильно ax 2 + c = 0.
Если c = 0, то квадратное уравнение выглядит так ax 2 + bx + 0 = 0, иначе его можно написать как ax 2 + bx = 0.
Если b = 0 и c = 0, то квадратное уравнение выглядит так ax 2 = 0.

Такие уравнения отличны от полного квадратного тем, что их левые части не содержат либо слагаемого с неизвестной переменной, либо свободного члена, либо и того и другого. Отсюда и их название — неполные квадратные уравнения.

Видео:МАТЕМАТИКА 8 класс - Квадратные Уравнения. Как решать Квадратные Уравнения? Формула КорнейСкачать

Решение неполных квадратных уравнений

Как мы уже знаем, есть три вида неполных квадратных уравнений:

ax 2 = 0, ему отвечают коэффициенты b = 0 и c = 0;
ax 2 + c = 0, при b = 0;
ax 2 + bx = 0, при c = 0.

Давайте рассмотрим по шагам, как решать неполные квадратные уравнения по видам.

Как решить уравнение ax 2 = 0

Начнем с решения неполных квадратных уравнений, в которых b и c равны нулю, то есть, с уравнений вида ax 2 = 0.

Уравнение ax 2 = 0 равносильно x 2 = 0. Такое преобразование возможно, когда мы разделили обе части на некое число a, которое не равно нулю. Корнем уравнения x 2 = 0 является нуль, так как 0 2 = 0. Других корней у этого уравнения нет, что подтверждают свойства степеней.

Таким образом, неполное квадратное уравнение ax 2 = 0 имеет единственный корень x = 0.

Пример 1. Решить −6x 2 = 0.

Замечаем, что данному уравнению равносильно x 2 = 0, значит исходное уравнение имеет единственный корень — нуль.
По шагам решение выглядит так:

Как решить уравнение ax 2 + с = 0

Обратим внимание на неполные квадратные уравнения вида ax 2 + c = 0, в которых b = 0, c ≠ 0. Мы давно знаем, что слагаемые в уравнениях носят двусторонние куртки: когда мы переносим их из одной части уравнения в другую, они надевает куртку на другую сторону — меняют знак на противоположный.

Еще мы знаем, что если обе части уравнения поделить на одно и то же число (кроме нуля) — у нас получится равносильное уравнение. Ну есть одно и то же, только с другими цифрами.

Держим все это в голове и колдуем над неполным квадратным уравнением (производим «равносильные преобразования»): ax 2 + c = 0:

перенесем c в правую часть: ax 2 = — c,
разделим обе части на a: x 2 = — c/а.

Ну все, теперь мы готовы к выводам о корнях неполного квадратного уравнения. В зависимости от значений a и c, выражение — c/а может быть отрицательным или положительным. Разберем конкретные случаи.

Если — c/а 2 = — c/а не имеет корней. Все потому, что квадрат любого числа всегда равен неотрицательному числу. Из этого следует, что при — c/а 0, то корни уравнения x 2 = — c/а будут другими. Например, можно использовать правило квадратного корня и тогда корень уравнения равен числу √- c/а, так как (√- c/а) 2 = — c/а. Кроме того, корнем уравнения может стать -√- c/а, так как (-√- c/а) 2 = — c/а. Ура, больше у этого уравнения нет корней.

Неполное квадратное уравнение ax 2 + c = 0 равносильно уравнению х 2 = -c/a, которое:

не имеет корней при — c/а 0.

В двух словах

Пример 1. Найти решение уравнения 8x 2 + 5 = 0.

Разделим обе части на 8:

В правой части осталось число со знаком минус, значит у данного уравнения нет корней.

Ответ: уравнение 8x 2 + 5 = 0 не имеет корней.

Как решить уравнение ax 2 + bx = 0

Осталось разобрать третий вид неполных квадратных уравнений, когда c = 0.

Неполное квадратное уравнение ax 2 + bx = 0 можно решить методом разложения на множители. Как разложить квадратное уравнение:

Разложим на множители многочлен, который расположен в левой части уравнения — вынесем за скобки общий множитель x.

Теперь можем перейти от исходного уравнения к равносильному x * (ax + b) = 0. А это уравнение равносильно совокупности двух уравнений x = 0 и ax + b = 0, последнее — линейное, его корень x = −b/a.

Таким образом, неполное квадратное уравнение ax 2 + bx = 0 имеет два корня:

Пример 1. Решить уравнение 0,5x 2 + 0,125x = 0

Это уравнение равносильно х = 0 и 0,5x + 0,125 = 0.

Решить линейное уравнение:

0,5x = 0,125,
х = 0,125/0,5

Значит корни исходного уравнения — 0 и 0,25.

Ответ: х = 0 и х = 0,25.

Как разложить квадратное уравнение

С помощью теоремы Виета можно получить формулу разложения квадратного трехчлена на множители. Выглядит она так:

Формула разложения квадратного трехчлена

Если x₁ и x₂ — корни квадратного трехчлена ax 2 + bx + c, то справедливо равенство ax 2 + bx + c = a (x − x₁) (x − x₂).

Видео:Как проверить корни квадратного уравнения. Как научиться применять т. Виета.Скачать

Дискриминант: формула корней квадратного уравнения

Чтобы найти результат квадратного уравнения, придумали формулу корней. Выглядит она так:

где D = b 2 − 4ac — дискриминант квадратного уравнения.

Эта запись означает:

Чтобы легко применять эту формулу, нужно понять, как она получилась. Давайте разбираться.

Алгоритм решения квадратных уравнений по формулам корней

Теперь мы знаем, что при решении квадратных уравнения можно использовать универсальную формулу корней — это помогает находить комплексные корни.

В 8 классе на алгебре можно встретить задачу по поиску действительных корней квадратного уравнения. Для этого важно перед использованием формул найти дискриминант и убедиться, что он неотрицательный, и только после этого вычислять значения корней. Если дискриминант отрицательный, значит уравнение не имеет действительных корней.

Алгоритм решения квадратного уравнения ax 2 + bx + c = 0:

вычислить его значение дискриминанта по формуле D = b 2 −4ac;
если дискриминант отрицательный, зафиксировать, что действительных корней нет;
если дискриминант равен нулю, вычислить единственный корень уравнения по формуле х = −b/2a;
если дискриминант положительный, найти два действительных корня квадратного уравнения по формуле корней

Чтобы запомнить алгоритм решения квадратных уравнений и с легкостью его использовать, давайте тренироваться!

Примеры решения квадратных уравнений

Как решать квадратные уравнения мы уже знаем, осталось закрепить знания на практике.

Пример 1. Решить уравнение −4x 2 + 28x — 49 = 0.

Найдем дискриминант: D = 28 2 — 4(-4)(-49) = 784 — 784 = 0
Так как дискриминант равен нулю, значит это квадратное уравнение имеет единственный корень
Найдем корень

Ответ: единственный корень 3,5.

Пример 2. Решить уравнение 54 — 6x 2 = 0.

Оставим неизвестное в одной части, остальное перенесем с противоположным знаком в другую

Ответ: два корня 3 и — 3.

Пример 3. Решить уравнение x 2 — х = 0.

Ответ: два корня 0 и 1.

Пример 4. Решить уравнение x 2 — 10 = 39.

Ответ: два корня 7 и −7.

Пример 5. Решить уравнение 3x 2 — 4x+94 = 0.

D = (-4) 2 — 4 * 3 * 94 = 16 — 1128 = −1112

Дискриминант отрицательный, поэтому корней нет.

Ответ: корней нет.

В школьной программе за 8 класс нет обязательного требования искать комплексные корни, но такой подход может ускорить ход решения. Если дискриминант отрицательный — сразу пишем ответ, что действительных корней нет и не мучаемся.

Видео:Квадратное уравнение. 1 урок.Скачать

Формула корней для четных вторых коэффициентов

Рассмотрим частный случай. Формула решения корней квадратного уравнения , где D = b 2 — 4ac, помогает получить еще одну формулу, более компактную, при помощи которой можно решать квадратные уравнения с четным коэффициентом при x. Рассмотрим, как появилась эта формула.

Например, нам нужно решить квадратное уравнение ax 2 + 2nx + c = 0. Сначала найдем его корни по известной нам формуле. Вычислим дискриминант D = (2n) 2 — 4ac = 4n 2 — 4ac = 4(n 2 — ac) и подставим в формулу корней:

2 + 2nx + c = 0″ height=»705″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc11a460e2f8354381151.png» width=»588″>

Для удобства вычислений обозначим выражение n 2 -ac как D₁. Тогда формула корней квадратного уравнения со вторым коэффициентом 2·n примет вид:

где D₁ = n 2 — ac.

Самые внимательные уже заметили, что D = 4D₁, или D₁= D/4. Проще говоря, D₁ — это четверть дискриминанта. И получается, что знак D1 является индикатором наличия или отсутствия корней квадратного уравнения.

Сформулируем правило. Чтобы найти решение квадратного уравнения со вторым коэффициентом 2n, нужно:

вычислить D₁= n 2 — ac;
если D₁ 0, значит можно найти два действительных корня по формуле

Видео:Неполные квадратные уравнения. Алгебра, 8 классСкачать

Формула Виета

Если в школьной геометрии чаще всего используется теорема Пифагора, то в школьной алгебре ведущую роль занимают формулы Виета. Теорема звучит так:

Сумма корней x 2 + bx + c = 0 равна второму коэффициенту с противоположным знаком, а произведение корней равняется свободному члену.

Если дано x 2 + bx + c = 0, где x₁ и x₂ являются корнями, то справедливы два равенства:

Знак системы, который принято обозначать фигурной скобкой, означает, что значения x₁ и x₂ удовлетворяют обоим равенствам.

Рассмотрим теорему Виета на примере: x 2 + 4x + 3 = 0.

Пока неизвестно, какие корни имеет данное уравнение. Но в соответствии с теоремой можно записать, что сумма этих корней равна второму коэффициенту с противоположным знаком. Он равен четырем, значит будем использовать минус четыре:

Произведение корней по теореме соответствует свободному члену. В данном случае свободным членом является число три. Значит:

Необходимо проверить равна ли сумма корней −4, а произведение 3. Для этого найдем корни уравнения x 2 + 4x + 3 = 0. Воспользуемся формулами для чётного второго коэффициента:
2 + 4x + 3 = 0″ height=»215″ src=»https://lh5.googleusercontent.com/E_X403ETh_88EANRWdQN03KRT8yxP2HO4HoCrxj__c8G0DqmNJ1KDRqtLH5Z1p7DtHm-rNMDB2tEs41D7RHpEV5mojDTMMRPuIkcW33jVNDoOe0ylzXdHATLSGzW4NakMkH2zkLE» width=»393″>

Получилось, что корнями уравнения являются числа −1 и −3. Их сумма равняется второму коэффициенту с противоположным знаком, а значит решение верное.
2 + 4x + 3 = 0″ height=»52″ src=»https://lh5.googleusercontent.com/VzGPXO9B0ZYrr9v0DpJfXwuzeZtjYnDxE_ma76PUC8o7jVWwa8kZjTJhq2Lof0TiJXAp_ny3yRwI_OyRzeucv9xUZ63yoozGPP4xd4OxvElVT7Pt-d6xL5w17e_mQNs5qZJQiwfG» width=»125″>

Произведение корней −1 и −3 по теореме Виета должно равняться свободному члену, то есть числу 3. Это условие также выполняется:
2 + 4x + 3 = 0″ height=»52″ src=»https://lh4.googleusercontent.com/Cq-LCFmY3YGNSan1VF3l3CqIeojoJYAvGAiTBWnzyoZu_xJFrF5NfQ3xCe59apJklw6uYbmQ4lAkBTeC-TJmEGicN3rgGtsezhuqdNiOWjZT39NziOB5uOmQr3cr9-5fNnepdZDo» width=»112″>

Результат проделанных вычислений в том, что мы убедились в справедливости выражения:

Когда дана сумма и произведение корней квадратного уравнения, принято начинать подбор подходящих корней. Теорема, обратная теореме Виета, при таких условиях может быть главным помощником. Вот она:

Обратная теорема Виета

Если числа x₁ и x₂ таковы, что их сумма равна второму коэффициенту уравнения x 2 + bx + c = 0, взятому с противоположным знаком, а их произведение равно свободному члену, то эти числа и есть корни x 2 + bx + c = 0.

Обычно вся суть обратных теорем в том самом выводе, которое дает первая теорема. Так, при доказательстве теоремы Виета стало понятно, что сумма x₁ и x₂ равна −b, а их произведение равно c. В обратной теореме это и есть утверждение.

Пример 1. Решить при помощи теоремы Виета: x 2 − 6x + 8 = 0.

2 − 6x + 8 = 0″ height=»59″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc101ce2e346034751939.png» width=»117″>

Когда у нас есть эти два равенства, можно подобрать подходящие корни, которые будут удовлетворять обоим равенствам системы.

Чтобы проще подобрать корни, нужно их перемножить. Число 8 можно получить путем перемножения чисел 4 и 2 либо 1 и 8. Но значения x₁ и x₂ надо подбирать так, чтобы они удовлетворяли и второму равенству тоже.

Можно сделать вывод, что значения 1 и 8 не подходят, так как они не удовлетворяют равенству x₁ + x₂ = 6. А значения 4 и 2 подходят обоим равенствам:

Значит числа 4 и 2 — корни уравнения x 2 − 6x + 8 = 0. p>

Упрощаем вид квадратных уравнений

Если мы ходили в школу всегда одной тропинкой, а потом вдруг обнаружили путь короче — это значит теперь у нас есть выбор: упростить себе задачу и сократить время на дорогу или прогуляться по привычному маршруту.

Так же и при вычислении корней квадратного уравнения. Ведь проще посчитать уравнение 11x 2 — 4 x — 6 = 0, чем 1100x 2 — 400x — 600 = 0.

Часто упрощение вида квадратного уравнения можно получить через умножение или деление обеих частей на некоторое число. Например, в предыдущем абзаце мы упростили уравнение 1100x 2 — 400x — 600 = 0, просто разделив обе части на 100.

Такое преобразование возможно, когда коэффициенты не являются взаимно простыми числами. Тогда принято делить обе части уравнения на наибольший общий делитель абсолютных величин его коэффициентов.

Покажем, как это работает на примере 12x 2 — 42x + 48 = 0. Найдем наибольший общий делитель абсолютных величин его коэффициентов: НОД (12, 42, 48) = 6. Разделим обе части исходного квадратного уравнения на 6, и придем к равносильному уравнению 2x 2 — 7x + 8 = 0. Вот так просто.

А умножение обеих частей квадратного уравнения отлично помогает избавиться от дробных коэффициентов. Умножать в данном случае лучше на наименьшее общее кратное знаменателей его коэффициентов. Например, если обе части квадратного уравнения

умножить на НОК (6, 3, 1) = 6, то оно примет более простой вид x 2 + 4x — 18 = 0.

Также для удобства вычислений можно избавиться от минуса при старшем коэффициенте квадратного уравнения — для этого умножим или разделим обе части на −1. Например, удобно от квадратного уравнения −2x 2 — 3x + 7 = 0 перейти к решению 2x 2 + 3x — 7 = 0.

Связь между корнями и коэффициентами

Мы уже запомнили, что формула корней квадратного уравнения выражает корни уравнения через его коэффициенты:

Из этой формулы, можно получить другие зависимости между корнями и коэффициентами.

Например, можно применить формулы из теоремы Виета:

Для приведенного квадратного уравнения сумма корней равна второму коэффициенту с противоположным знаком, а произведение корней — свободному члену. Например, по виду уравнения 3x 2 — 7x + 22 = 0 можно сразу сказать, что сумма его корней равна 7/3, а произведение корней равно 22/3.

Можно активно использовать уже записанные формулы и с их помощью получить ряд других связей между корнями и коэффициентами квадратного уравнения. Таким образом можно выразить сумму квадратов корней квадратного уравнения через его коэффициенты: