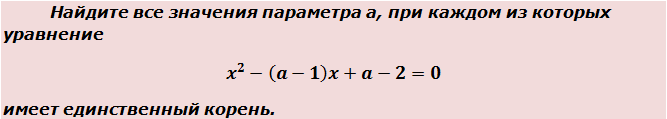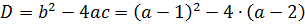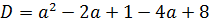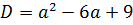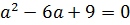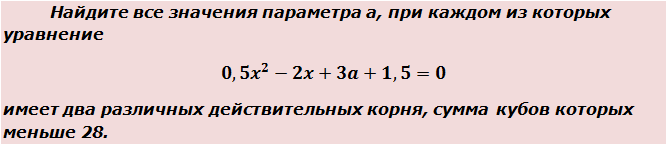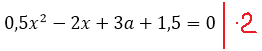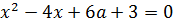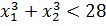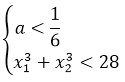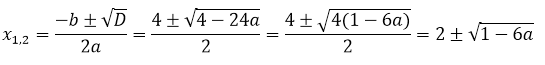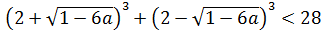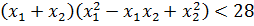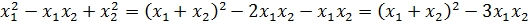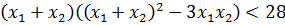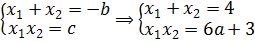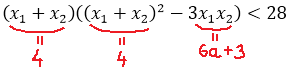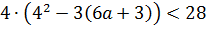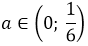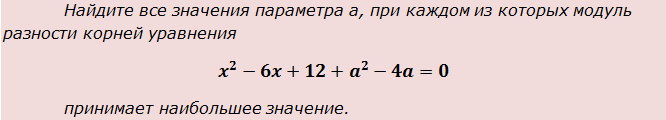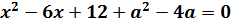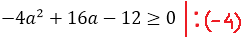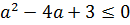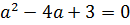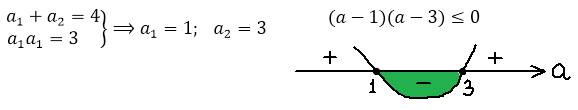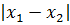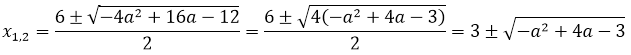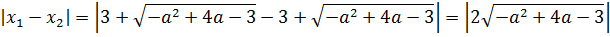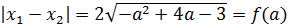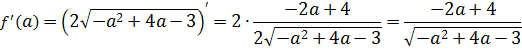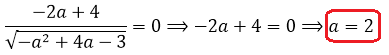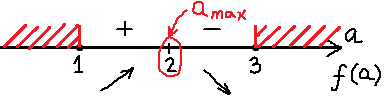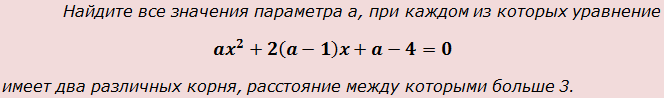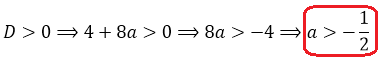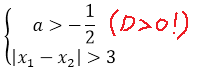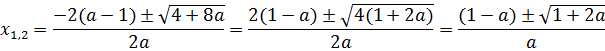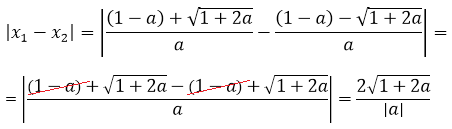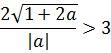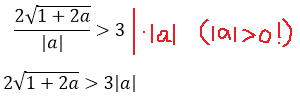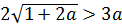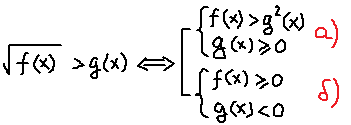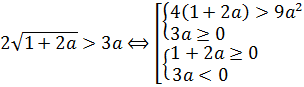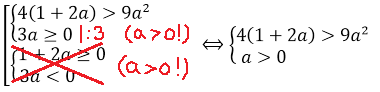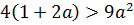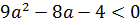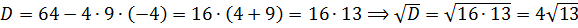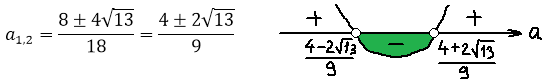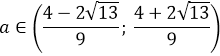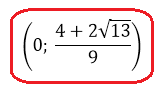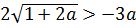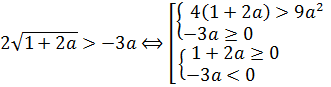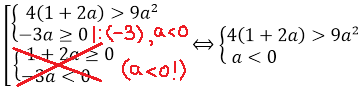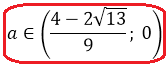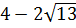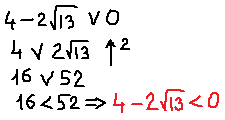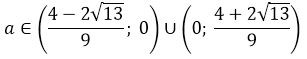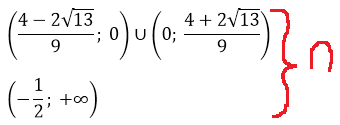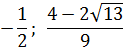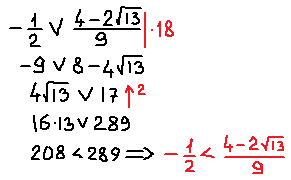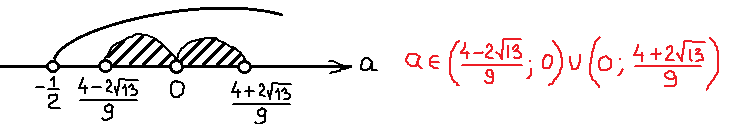Квадратные уравнения с параметром 8 класс примеры с решением (6 видео)

Содержание

Квадратные уравнения с параметром
Понятие уравнения с параметром и его решения
Примеры
Конспект «Решение квадратных уравнений с параметрами» (8 класс)
Краткое описание документа:
Квадратные уравнения с параметром
📹 Видео

Видео:#119 Урок 44. Параметры. Квадратные уравнения с параметрами. Алгебра 8 класс. Математика.Скачать

Квадратные уравнения с параметром

Понятие уравнения с параметром и его решения

Часто на практике создаётся такая математическая модель, в которой приходится решать не одно, а целое «семейство» похожих уравнений.

Рассмотрим несложный пример.

Пусть нам дан прямоугольный участок площадью a. С точки зрения практической, мы хотим обнести участок забором, т.е. нас интересует зависимость периметра от длины x при некоторой площади a (ширина будет равна $frac$):

Допустим, у нас есть материалы, чтобы соорудить забор длиной 100 м.

Это – простейшее уравнение с параметром, в котором один из коэффициентов не задан конкретным числом.

Уравнение относительно переменной x с параметром a – это уравнение F(x,a), в котором значение a не определено и также является переменной величиной.

Решить уравнение с параметром – это найти множество корней $$ для любого значения параметра a .

Решим наше уравнение. Найдём дискриминант:

$$ D = 50^2-4a = 2500-4a = 4(625-a) $$

Чтобы решения существовали, потребуем:

$$ D ge 0 Rightarrow 625-a ge 0 Rightarrow a le 625 $$

При $a lt 625$ два корня $x_ = 25 pm sqrt$

При a = 625 один корень $x_0 = 25$

При $a gt 625$ решений нет

Наша модель немного усложнится, если мы поставим условия, чтобы площадь и длина были строго положительными:

Исследуем решение. Полученный корень $x_2 = 25+ sqrt ge 25 gt 0$ — положительный. И $x_1 = 25- sqrt$ при $0 lt a lt 625$ меняется в пределах $0 lt x_1 lt 25$, т.е. также положительный.

Запишем ответ для модели с условиями:

При $0 lt a lt 625$ два корня $x_ = 25 pm sqrt$

При a = 625 один корень $x_0$ = 25

При $a gt 625$ решений нет

Ответ изменился незначительно, но чтобы его записать, нам пришлось провести дополнительное исследование.

Решить уравнение с параметром F(x,a) при дополнительных условиях на переменную x и параметр a – это найти допустимое множество корней $$ для любого допустимого значения параметра a .

Заметим, что согласно полученным результатам, максимальная площадь, которую мы можем огородить нашим забором длиной 100 м, равна a = 625 $м^2$. Участок при этом представляет собой квадрат с длиной $x_0 = 25$ м и шириной $ frac = 25$ м.

Примеры

Пример 1. При каких p квадрат разности корней уравнения $x^2-4x+p = 0$ равен 32?

Пусть $x_1, x_2$ — корни уравнения. По теореме Виета и условию задачи:

$$ <left< begin x_1+x_2 = 4 \ x_1 x_2 = p \ x_1^2-x_2^2 = 32 end right.> Rightarrow <left< begin x_1+x_2 = 4 \ x_1 x_2 = p \ (x_1+x_2 )(x_1-x_2 ) = 32 end right.> Rightarrow <left< begin x_1+x_2 = 4 \ x_1-x_2 = 8 \ x_1 x_2 = p end right.> Rightarrow $$

$$ Rightarrow <left< begin 2x_1 = 4+8 = 12 \ 2x_2 = 4-8 = -4 \ x_1 x_2 = p end right.> Rightarrow <left< begin x_1 = 6 \ x_2 = -2 \ p = 6 cdot (-2) = -12 end right.> $$

Пример 2. При каких значениях a уравнение

имеет один корень? Найдите этот корень.

$$ D = (a+2)^2-4(a+5) = a^2+4a+4-4a-20 = a^2-16 $$

Уравнение имеет один корень, если D = 0:

$$ a^2-16 = 0 Rightarrow a = pm 4 $$

При a = -4 уравнение имеет вид $x^2+2x+1 = 0$, т.е. $(x+1)^2 = 0$, $x_0 = -1$

При a = 4 уравнение имеет вид $x^2-6x+9 = 0$, т.е. $(x-3)^2 = 0, x_0 = 3$

При a = -4, $x_0$ = -1

При a = 4, $x_0$ = 3

Пример 3. Найдите такое p, чтобы уравнения

$$ x^2+x+p = 0 и x^2+px+1 = 0 $$

имели общий корень. Найдите этот корень.

Общий корень означает, что параболы пересекаются в точке, лежащей на оси OX.

$$ x(1-p) = 1-p Rightarrow left[ begin <left< begin p = 1 \ x in Bbb R — любой end right.> \ <left< begin p neq 1 \ x = 1 end right.> end right. $$

При p = 1 уравнения совпадают $x^2+x+1 = 0$, но решений не имеют, т.к. $D lt 0$.

При x = 1 уравнения парабол имеют вид: $p+2 = 0 Rightarrow p = -2$.

При p = 2 уравнения имеют общий корень x = 1.

Пример 4. Найдите все целые значения a, при которых уравнение $frac = frac$ имеет решение.

Особая точка: a = 4. Уравнение $x^2-2x+4 = 0$ решений не имеет, т.к. $D lt 0$.

Решаем уравнение в общем виде:

Потребуем $D ge 0$

$$ -4(a-3)(a-1) ge 0 Rightarrow (a-3)(a-1) le 0 $$

Начертим график параболы

Значение $f(a) le 0$ не положительно, только на отрезке

Это значит, что $D ge 0$, и уравнение имеет решения, только при трёх целочисленных a $in$

При a = 1 и a = 3 D = 0, уравнение имеет вид $x^2-2x+1 = 0$ и одно решение $x_0 = 1$.

При a = 2 уравнение имеет вид: $x^2-2x = 0 Rightarrow x(x-2) = 0 Rightarrow left[ begin x_1 = 0 \ x_2 = 2 end right. $

При a = 1 и a = 3 один корень $x_0 = 1$

При a = 2 два корня $x_1 = 0, x_2 = 2$

При всех других целых a уравнение решений не имеет.

Пример 5. При каких b и c уравнение $x^2+bx+c = 0$ имеет корнями b и c?

По условию $x_1 = b, x_2 = c$

По теореме Виета:

$$ <left< begin x_1+x_2 = b+c = -b \ x_1 x_2 = bc = c end right.> Rightarrow <left< begin c = -2b = -2 \ b = 1end right.> $$

Уравнение $x^2+x-2 = 0$ имеет корнями 1 и -2.

Ответ: b = 1, c = -2

Пример 6. Найдите все значения параметра a, при которых уравнения

$$ x^2+(a^2+3a+7)x = 0 и x^2+(4a+19)x+(a^2+7a-44) = 0 $$

имеют один и те же решения.

Старшие коэффициенты парабол одинаковы и равны 1.

Параболы будут иметь одинаковые решения в том случае, если будут полностью совпадать, т.е.:

$$ <left< begin a^2+3a+7 = 4a+19 \ 0 = a^2+7a-44 end right.> Rightarrow <left< begin a^2-a-12 = 0 \ a^2+7a-44 = 0 end right.> Rightarrow <left< begin (a-4)(a+3) = 0 \ (a-4)(a+11) = 0 end right.> Rightarrow a = 4 $$

Кроме того, они могли бы совпадать, если бы все переменные коэффициенты одновременно стали равны 0:

$$ <left< begin a^2+3a+7 = 0 \ 4a+19 = 0 \ a^2+7a-44 = 0 end right.> Rightarrow <left< begin D lt 0, a in varnothing \ a = — frac \ a = end right.> Rightarrow a in varnothing $$

Пример 7. Решите уравнение:

При a = 1 уравнение имеет вид $x^2 = 0$ и один корень $x_0 = 0$

Видео:Уравнения с параметром. Алгебра, 8 классСкачать

Конспект «Решение квадратных уравнений с параметрами» (8 класс)

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Рабочие листы и материалы для учителей и воспитателей

Более 300 дидактических материалов для школьного и домашнего обучения

Тема урока: решение квадратных уравнений с параметрами.

Тип урока: комбинированный.

Планируемые результаты обучения:

— личностные: логичность мышления, умение работать в проблемной ситуации;

— предметные: формировать умение решать квадратные уравнения с параметром;

— метапредметные: формирование информационной, коммуникативной и учебной компетентности учащихся, умения работать с имеющейся информацией в новой ситуации.

Этапы урока (время)

1. Организационный момент.

Приветствует учащихся, организует рабочее место,

Учащиеся настраиваются на работу.

2. Актуали-зация теоретических знаний.

Проводится опрос по теории

— Какое уравнение называется квадратным?

— Квадратным или линейным является уравнение

а) при b=6; б)0; в) b=0,5;

-Какое квадратное уравнение называется приведенным?

-Какое выражение называют дискриминантом?

-Сколько корней может иметь квадратное уравнение? (формулы).

-Теорема Виета и обратное утверждение.(записать)

Учащиеся предлагают различные варианты решения, говорят о трудностях, которые у них возникли.

Формировать личную мотивацию к учению.

Структурировать знания по данной теме

Учебное сотрудничество с учителем

3. Объяснение нового материа-ла.

При решении квадратного уравнения с параметрами контрольными будут те значения параметра, при которых коэффициент при обращается в 0. Дело в том, что если этот коэффициент равен 0, то уравнение превращается в линейное и решается по соответствующему алгоритму; если же этот коэффициент отличен от нуля, то имеем квадратное уравнение, которое решается по иному алгоритму. Дальнейшее решение зависит от D .

Учащиеся формулируют цель урока: «Научиться решать уравнения с параметром».

Взаимоконтроль и самоконтроль

Умение структурировать знания

Учебное сотрудничество с учителем и сверстниками, управление поведением партнера

4. Приме-нение знаний и умений в новой ситуации

Решение: Здесь коэффициент перед отличен от , значит, данное уравнение при любых значениях параметра является квадратным. Найдем дискриминант:

D =

D , значит, квадратное уравнение имеет два различных корня.

p +2 и p -1

Ответ: при любых значениях р p +2 ; p -1.

Пример 2. Решить уравнение p .

Решение: Мы не можем утверждать, что данное уравнение является квадратным. Рассмотрим контрольное значение р=0, имеем два случая.

Если р=0, то получается уравнение вида 0 + х=1.

Если р≠0. То уравнение является квадратным, можно применять формулу D = —

4р(-1)=1-2р+ +4р= ; ; .

Ответ: при р=0 х=1, при р≠0 ; .

Пример 3. Решить уравнение

Найдем значения параметра, обращающие в нуль коэффициент при х

Решим уравнение при а=1

0 × х 2 +2(2 × 1+1)х+4 × 1+3=0 Û 6х+7=0 Û .

Найдем значения параметра, обращающие в нуль дискриминант уравнения

4(5а+4)=0 Û .

Решим уравнение при , в этом случае уравнение будет иметь один действительный корень

Û Û

9х 2 +6х+1=0 Û (3х+1) 2 =0 Û .

Решим уравнение при а ¹ 1, . В этом случае D

Решим уравнение при а ¹ 1, . В этом случае уравнение имеет два действительных корня

Ответ: 1) при , ;

2) при а=1, ;

3) при , действительных корней нет;

4) при и а ¹ 1, .

Пример 4. При каких значениях m ровно один из корней уравнения

Решение: Если нуль является корнем уравнения, значит квадратный трехчлен =0 обращается в нуль. =-3, =3.

Найдем второй корень при найденных значениях m .

Если m =3, то получаем =0, =-6.

Если m =-3, то получаем =0, которое имеет два кратных корня равных 0.

5. Закрепле-ние матери-ала

Работа в группах.

( а + 1 ) х 2 – 2 ( а + 9 ) х + 9 = 0;

С последующей проверкой.

Работа в группах. Проблемный диалог. Задают и отвечают на вопросы.

Контроль, коррекция, оценка

Учебное сотрудничество с учителем и сверстниками, управление поведением партнера

6. Домаш-нее задание.

1. При каких значениях а уравнение (а+2) +2(а+2)х+2=0 имеет один корень?

2.Решить уравнение .

3. Решить уравнение

4. Решить уравнение ( 2 — b -6) = 4( b +1) x -2.

Объясняет какие номера обязательные и какие можно взять по выбору.

Учащиеся записывают домашнее задание и определяют для себя уровни заданий.

7. Итог урока. (1мин)

Какие цели стояли на уроке?

Достиг ли каждый из вас цели урока?

Фиксирую проблемы для следующего урока.

Самостоятельно определяют насколько достигнуты цели урока.

Формировать адекватную самооценку.

Формировать умения планировать свою работу.

Формулировать собственное мнение и аргументировать его.

Формулировать познавательную цель.

Учащимся предлагается по желанию продолжить предложение:

На уроке я научился (научилась) …

На уроке мне понравилось …

На уроке мне пригодились знания….

Для меня было сложно…

С урока я ухожу с … настроением!

Учащиеся продолжают предложения.

Смыслообразование, формирование положительного отношения к процессу познания

Оценка- выделение и осознание учащимися того, что уже усвоено и что еще подлежит усвоению.

Рефлексия способов и условий действия, контроль и оценка процесса и результатов деятельности.

Краткое описание документа:

Тема урока: решение квадратных уравнений с параметрами.

Тип урока: комбинированный.

Планируемые результаты обучения:

личностные: логичность мышления, умение работать в проблемной ситуации;

предметные: формировать умение решать квадратные уравнения с параметром;

метапредметные: формирование информационной, коммуникативной и учебной компетентности учащихся, умения работать с имеющейся информацией в новой ситуации.

1. Организационный момент.

Приветствует учащихся, организует рабочее место,

Учащиеся настраиваются на работу.

2. Актуали-зация теоретических знаний.

Проводится опрос по теории

— Какое уравнение называется квадратным?

— Квадратным или линейным является уравнение

а) при b=6; б)0; в) b=0,5;

-Какое квадратное уравнение называется приведенным?

-Какое выражение называют дискриминантом?

-Сколько корней может иметь квадратное уравнение? (формулы).

-Теорема Виета и обратное утверждение.(записать)

Учащиеся предлагают различные варианты решения, говорят о трудностях, которые у них возникли.

Формировать личную мотивацию к учению.

Структурировать знания по данной теме

Учебное сотрудничество с учителем

3. Объяснение нового материа-ла.

Учащиеся формулируют цель урока: «Научиться решать уравнения с параметром».

Взаимоконтроль и самоконтроль

Умение структурировать знания

Учебное сотрудничество с учителем и сверстниками, управление поведением партнера

4. Приме-нение знаний и умений в новой ситуации

D =

D , значит, квадратное уравнение имеет два различных корня.

p +2 и p -1

Ответ: при любых значениях р p +2 ; p -1.

Пример 2. Решить уравнение p .

Если р=0, то получается уравнение вида 0+ х=1.

Если р≠0. То уравнение является квадратным, можно применять формулу D =—

4р(-1)=1-2р++4р=; ; .

Ответ: при р=0 х=1, при р≠0 ; .

Найдем значения параметра, обращающие в нуль коэффициент при х

Решим уравнение при а=1

0  х 2 +2(2  1+1)х+4  1+3=0  6х+7=0  .

Найдем значения параметра, обращающие в нуль дискриминант уравнения

4(5а+4)=0  .

Решим уравнение при , в этом случае уравнение будет иметь один действительный корень

 

9х 2 +6х+1=0  (3х+1) 2 =0  .

Решим уравнение при а  1, . В этом случае D  1, . В этом случае уравнение имеет два действительных корня

Ответ: 1) при , ;

2) при а=1, ;

3) при , действительных корней нет;

4) при и а  1, .

Пример 4. При каких значениях m ровно один из корней уравнения

Решение: Если нуль является корнем уравнения, значит квадратный трехчлен =0 обращается в нуль. =-3, =3.

Найдем второй корень при найденных значениях m .

Если m =3, то получаем =0, =-6.

Если m =-3, то получаем =0, которое имеет два кратных корня равных 0.

5. Закрепле-ние матери-ала

Работа в группах.

( а + 1 ) х 2 – 2 ( а + 9 ) х + 9 = 0;

С последующей проверкой.

Работа в группах. Проблемный диалог. Задают и отвечают на вопросы.

Контроль, коррекция, оценка

Учебное сотрудничество с учителем и сверстниками, управление поведением партнера

6. Домаш-нее задание.

1.При каких значениях а уравнение (а+2) +2(а+2)х+2=0 имеет один корень?

2.Решить уравнение .

3. Решить уравнение

4. Решить уравнение ( 2— b -6) = 4( b +1) x -2.

Объясняет какие номера обязательные и какие можно взять по выбору.

Учащиеся записывают домашнее задание и определяют для себя уровни заданий.

7. Итог урока. (1мин)

Какие цели стояли на уроке?

Достиг ли каждый из вас цели урока?

Фиксирую проблемы для следующего урока.

Самостоятельно определяют насколько достигнуты цели урока.

Формировать адекватную самооценку.

Формировать умения планировать свою работу.

Формулировать собственное мнение и аргументировать его.

Формулировать познавательную цель.

Учащимся предлагается по желанию продолжить предложение:

На уроке я научился (научилась) …

На уроке мне понравилось …

На уроке мне пригодились знания….

Для меня было сложно…

С урока я ухожу с … настроением!

Учащиеся продолжают предложения.

Смыслообразование, формирование положительного отношения к процессу познания

Оценка- выделение и осознание учащимися того, что уже усвоено и что еще подлежит усвоению.

Рефлексия способов и условий действия, контроль и оценка процесса и результатов деятельности.

Видео:Решаем квадратное уравнение с параметромСкачать

Квадратные уравнения с параметром

Задачи с параметрами. Простейшие задачи на квадратный трёхчлен.

Сегодня мы рассмотрим задачи на квадратный трёхчлен, про который, в зависимости от параметра, надо будет что-то выяснить. Это «что-то» может быть самым разнообразным, насколько только хватит фантазии у составителей задачи. Это самый простой тип задач с параметрами. И, если на ЕГЭ вам попалась такая — считайте, что вам повезло!

Но, прежде чем приступать к разбору самих задач, ответьте сами себе на такие простые вопросы:

— Что такое квадратное уравнение, как оно выглядит и как решается?

— Что такое дискриминант и куда его пристроить?

— Что такое теорема Виета и где её можно применить?

Если вы верно отвечаете на эти простые вопросы, то 50% успеха в решении параметрических задач на квадратный трёхчлен вам обеспечены! А остальные 50% — это обычная алгебра и арифметика: раскрытие скобок, приведение подобных, решение уравнений, неравенств и систем и т.д.

Для начала рассмотрим совсем безобидную задачку. Для разминки. 🙂

Пример 1

Приступаем к решению. Во-первых, чтобы в будущем не накосячить в коэффициентах, всегда полезно выписать их отдельно. Прямо в столбик. Вот так:

Да-да! Часть коэффициентов в уравнении (а именно — b и с) зависит от параметра. В этом как раз и состоит вся фишка таких задач. А теперь снова въедливо перечитываем условие. Ключевой зацепкой в формулировке задания являются слова «единственный корень». И когда же квадратное уравнение имеет единственный корень? Подключаем наши теоретические знания о квадратных уравнениях. Только в одном единственном случае — когда его дискриминант равен нулю.

Осталось составить выражение для дискриминанта и приравнять его к нулю. Поехали!

Теперь надо приравнять наш дискриминант к нулю:

Можно, конечно, решать это квадратное уравнение через дискриминант, а можно немного схитрить. На что у нас похожа левая часть, если как следует присмотреться? Она у нас похожа на квадрат разности (a-3) 2 !

Респект внимательным! Верно! Если заменить наше выражение слева на (a-3) 2 , то уравнение будет решаться в уме!

Вот и всё. Это значит, что единственный корень наше квадратное уравнение с параметром будет иметь только в одном единственном случае — когда значение параметра «а» равно тройке.)

Это был разминочный пример. Чтобы общую идею уловить.) Теперь будет задачка посерьёзнее.

Пример 2

Вот такая задачка. Начинаем распутывать. Первым делом выпишем наше квадратное уравнение:

0,5x 2 — 2x + 3a + 1,5 = 0

Самым логичным шагом, было бы умножить обе части на 2. Тогда у нас исчезнут дробные коэффициенты и само уравнение станет посимпатичнее. Умножаем:

Выписываем в столбик наши коэффициенты a, b, c:

Видно, что коэффициенты a и b у нас постоянны, а вот свободный член с зависит от параметра «а»! Который может быть каким угодно — положительным, отрицательным, целым, дробным, иррациональным — всяким!

А теперь, чтобы продвинуться дальше, вновь подключаем наши теоретические познания в области квадратных уравнений и начинаем рассуждать. Примерно так:

«Для того чтобы сумма кубов корней была меньше 28, эти самые корни, во-первых, должны существовать. Сами по себе. В принципе. А корни у квадратного уравнения существуют, тогда и только тогда, когда его дискриминант неотрицательный. Кроме того, в задании говорится о двух различных корнях. Эта фраза означает, что наш дискриминант обязан быть не просто неотрицательным, а строго положительным!»

Если вы рассуждаете таким образом, то вы движетесь правильным курсом! Верно.) Составляем условие положительности для дискриминанта:

Полученное условие говорит нам о том, что два различных корня у нашего уравнения будет не при любых значениях параметра «а», а только при тех, которые меньше одной шестой! Это глобальное требование, которое должно выполняться железно. Неважно, меньше 28 наша сумма кубов корней или больше. Значения параметра «а», большие или равные 1/6, нас заведомо не устроят. Гуд.) Соломки подстелили. Движемся дальше.

Теперь приступаем к загадочной сумме кубов корней. По условию она у нас должна быть меньше 28. Так и пишем:

Значит, для того чтобы ответить на вопрос задачи, нам надо совместно рассмотреть два условия:

А дальше начинаем отдельно работать с этой самой суммой кубов. Есть два способа такой работы: первый способ для трудолюбивых и второй способ — для внимательных.

Способ для трудолюбивых заключается в непосредственном нахождении корней уравнения через параметр. Прямо по общей формуле корней. Вот так:

Теперь составляем нужную нам сумму кубов найденных корней и требуем, чтобы она была меньше 28:

А дальше — обычная алгебра: раскрываем сумму кубов по формуле сокращённого умножения, приводим подобные, сокращаем и т.д. Если бы корни нашего уравнения получились покрасивее, без радикалов, то такой «лобовой» способ был бы неплох. Но проблема в том, что наши корни выглядят немного страшновато. И подставлять их в сумму кубов как-то неохота, да. Поэтому, для того чтобы избежать этой громоздкой процедуры, я предлагаю второй способ — для внимательных.

Для этого раскрываем сумму кубов корней по соответствующей формуле сокращенного умножения. Прямо в общем виде:

А дальше проделываем вот такой красивый фокус: во вторых скобках выражаем сумму квадратов корней через сумму корней и их произведение. Вот так:

Казалось бы, и что из этого? Сейчас интересно будет! Давайте, посмотрим ещё разок на наше уравнение. Как можно внимательнее:

Чему здесь равен коэффициент при x 2 ? Правильно, единичке! А как такое уравнение называется? Правильно, приведённое! А, раз приведённое, то, стало быть, для него справедлива теорема Виета:

Вот и ещё одна теорема нам пригодилась! Теперь, прямо по теореме Виета, подставляем сумму и произведение корней в наше требование для суммы кубов:

Осталось раскрыть скобки и решить простенькое линейное неравенство:

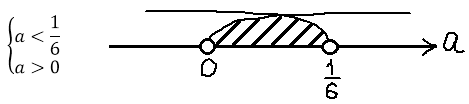
Вспоминаем, что ещё у нас есть глобальное требование a 0 необходимо пересечь с условием a . Рисуем картинку, пересекаем, и записываем окончательный ответ.

Да. Вот такой маленький интервальчик. От нуля до одной шестой… Видите, насколько знание теоремы Виета, порой, облегчает жизнь!

Вот вам небольшой практический совет: если в задании говорится о таких конструкциях, как сумма, произведение, сумма квадратов, сумма кубов корней, то пробуем применить теорему Виета. В 99% случаев решение значительно упрощается.

Это были довольно простые примеры. Чтобы суть уловить. Теперь будут примеры посолиднее.

Например, такая задачка из реального варианта ЕГЭ:

Пример 3

Что, внушает? Ничего не боимся и действуем по нашему излюбленному принципу: «Не знаешь, что нужно, делай что можно!»

Опять аккуратно выписываем все коэффициенты нашего квадратного уравнения:

А теперь вчитываемся в условие задачи и находим слова «модуль разности корней уравнения». Модуль разности нас пока не волнует, а вот слова «корней уравнения» примем во внимание. Раз говорится о корнях (неважно, двух одинаковых или двух различных), то наш дискриминант обязан быть неотрицательным! Так и пишем:

Что ж, аккуратно расписываем наш дискриминант через параметр а:

А теперь решаем квадратное неравенство. По стандартной схеме, через соответствующее квадратное уравнение и схематичный рисунок параболы:

Значит, для того чтобы у нашего уравнения в принципе имелись хоть какие-то корни, параметр а должен находиться в отрезке [-1; 3]. Это железное требование. Хорошо. Запомним.)

А теперь приступаем к этому самому модулю разности корней уравнения. От нас хотят, чтобы вот такая штука

принимала бы наибольшее значение. Для этого, ничего не поделать, но теперь нам всё-таки придётся находить сами корни и составлять их разность: x₁ — x₂. Теорема Виета здесь в этот раз бессильна.

Что ж, считаем корни по общей формуле:

Дальше составляем модуль разности этих самых корней:

Теперь вспоминаем, что корень квадратный — величина заведомо неотрицательная. Стало быть, без ущерба для здоровья, модуль можно смело опустить. Итого наш модуль разности корней выглядит так:

И эта функция f(a) должна принимать наибольшее значение. А для поиска наибольшего значения у нас есть такой мощный инструмент, как производная! Вперёд и с песнями!)

Дифференцируем нашу функцию и приравниваем производную к нулю:

Получили единственную критическую точку a = 2. Но это ещё не ответ, так как нам ещё надо проверить, что найденная точка и в самом деле является точкой максимума! Для этого исследуем знаки нашей производной слева и справа от двойки. Это легко делается простой подстановкой (например, а = 1,5 и а = 2,5).

Слева от двойки производная положительна, а справа от двойки — отрицательна. Это значит, что наша точка a = 2 и вправду является точкой максимума. Заштрихованная зона на картинке означает, что нашу функцию мы рассматриваем только на отрезке [1; 3]. Вне этого отрезка нашей функции f(a) попросту не существует. Потому, что в заштрихованной области наш дискриминант отрицательный, и разговоры о каких-либо корнях (и о функции тоже) бессмысленны. Это понятно, думаю.

Всё. Вот теперь наша задача полностью решена.

Здесь было применение производной. А бывают и такие задачи, где приходится решать уравнения либо неравенства с так ненавистными многими учениками модулями и сравнивать некрасивые иррациональные числа с корнями. Главное — не бояться! Разберём похожую злую задачку (тоже из ЕГЭ, кстати).

Пример 4

Итак, приступаем. Первым делом замечаем, что параметр а ни в коем случае не может быть равен нулю. Почему? А вы подставьте в исходное уравнение вместо а нолик. Что получится?

Получили линейное уравнение, имеющее единственный корень x=2. А это уже совсем не наш случай. От нас хотят, чтобы уравнение имело два различных корня, а для этого нам необходимо, чтобы оно, как минимум, было хотя бы квадратным.)

При всех остальных значениях параметра наше уравнение будет вполне себе квадратным. И, следовательно, чтобы оно имело два различных корня, необходимо (и достаточно), чтобы его дискриминант был положительным. То есть, первое наше требование будет D > 0.

А далее по накатанной колее. Считаем дискриминант:

D = 4(a-1) 2 — 4a(a-4) = 4a 2 -8a+4-4a 2 +16a = 4+8a

Вот так. Значит, наше уравнение имеет два различных корня тогда и только тогда, когда параметр a > -1/2. При прочих «а» у уравнения будет либо один корень, либо вообще ни одного. Берём на заметку это условие и движемся дальше.

Далее в задаче идёт речь о расстоянии между корнями. Расстояние между корнями, в математическом смысле, означает вот такую величину:

Зачем здесь нужен модуль? А затем, что любое расстояние (что в природе, что в математике) — величина неотрицательная. Причём здесь совершенно неважно, какой именно корень будет стоять в этой разности первым, а какой вторым: модуль — функция чётная и сжигает минус. Точно так же, как и квадрат.

Значит, ответом на вопрос задачи является решение вот такой системы:

Теперь, ясен перец, нам надо найти сами корни. Здесь тоже всё очевидно и прозрачно. Аккуратно подставляем все коэффициенты в нашу общую формулу корней и считаем:

Отлично. Корни получены. Теперь начинаем формировать наше расстояние:

Наше расстояние между корнями должно быть больше трёх, поэтому теперь нам надо решить вот такое неравенство:

Неравенство — не подарок: модуль, корень… Но и мы всё-таки уже решаем серьёзную задачу №18 из ЕГЭ! Делаем всё что можно, чтобы максимально упростить внешний вид неравенства. Мне здесь больше всего не нравится дробь. Поэтому первым делом я избавлюсь от знаменателя, умножив обе части неравенства на |a|. Это можно сделать, поскольку мы, во-первых, в самом начале решения примера договорились, что а ≠ 0, а во-вторых, сам модуль — величина неотрицательная.

Итак, смело умножаем обе части неравенства на положительное число |a|. Знак неравенства сохраняется:

Вот так. Теперь в нашем распоряжении имеется иррациональное неравенство с модулем. Ясное дело, для того чтобы решить его, надо избавляться от модуля. Поэтому придётся разбивать решение на два случая — когда параметр а, стоящий под модулем, положителен и когда отрицателен. Другого пути избавиться от модуля у нас, к сожалению, нет.

Случай 1 (a>0, |a|=a)

В этом случае наш модуль раскрывается с плюсом, и неравенство (уже без модуля!) принимает следующий вид:

Неравенство имеет структуру: «корень больше функции». Такие иррациональные неравенства решаются по следующей стандартной схеме:

Отдельно рассматривается случай а), когда обе части неравенства возводятся в квадрат и правая часть неотрицательна и отдельно — случай б), когда правая часть всё-таки отрицательна, но зато сам корень при этом извлекается.) И решения этих двух систем объединяются.

Тогда, в соответствии с этой схемой, наше неравенство распишется вот так:

А теперь можно существенно упростить себе дальнейшую работу. Для этого вспомним, что в случае 1 мы рассматриваем только a>0. С учётом этого требования, вторую систему можно вообще вычеркнуть из рассмотрения, поскольку, второе неравенство в ней (3a 0 и a

Упрощаем нашу совокупность с учётом главного условия a>0:

Вот так. А теперь решаем самое обычное квадратное неравенство:

Нас интересует промежуток между корнями. Стало быть,

Отлично. Теперь этот промежуток пересекаем со вторым условием системы a>0:

Есть. Таким образом, первым кусочком ответа к нашему неравенству (а пока не ко всей задаче!) будет вот такой интервал:

Всё. Случай 1 разложен по полочкам. Переходим к случаю 2.

Случай 2 (a

В этом случае наш модуль раскрывается с минусом, и неравенство принимает следующий вид:

Опять имеем структуру: «корень больше функции». Применяем нашу стандартную схему с двумя системами (см. выше):

С учётом общего требования a

А дальше снова решаем обычное квадратное неравенство:

И опять сокращаем себе работу. Ибо оно у нас уже решено в процессе разбора случая 1! Решение этого неравенства выглядело вот так:

Осталось лишь пересечь этот интервал с нашим новым условием a

Вот и второй кусочек ответа готов:

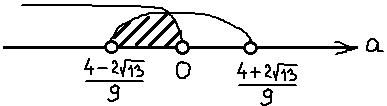
Кстати сказать, как я узнал, что ноль лежит именно между нашими иррациональными корнями? Легко! Очевидно, что правый корень заведомо положителен. А что касается левого корня, то я просто в уме сравнил иррациональное число

с нулём. Вот так:

А теперь объединяем оба найденных интервала. Ибо мы решаем совокупность (а не систему):

Готово дело. Эти два интервала — это пока ещё только решение неравенства

Кто забыл, данное неравенство отвечает у нас за расстояние между корнями нашего уравнения. Которое должно больше 3. Но! Это ещё не ответ!

Ещё у нас есть условие положительного дискриминанта! Неравенство a>-1/2, помните? Это значит, что данное множество нам ещё надо пересечь с условием a>-1/2. Иными словами, теперь мы должны пересечь два множества:

Но есть одна проблемка. Мы не знаем, как именно расположено на прямой число -1/2 относительно левого (отрицательного) корня. Для этого нам придётся сравнить между собой два числа:

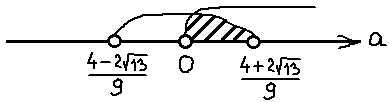
Поэтому сейчас берём черновик и начинаем сравнивать наши числа. Примерно так:

Это значит, что дробь -1/2 на числовой прямой находится левее нашего левого корня. И картинка к окончательному ответу задачи будет какая-то вот такая: