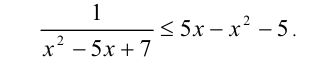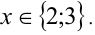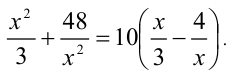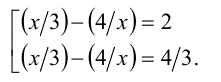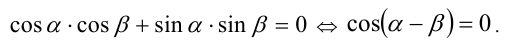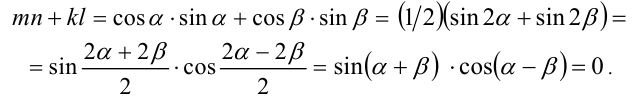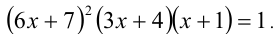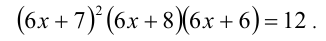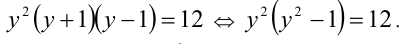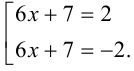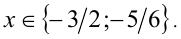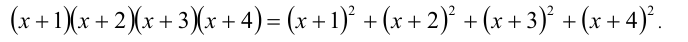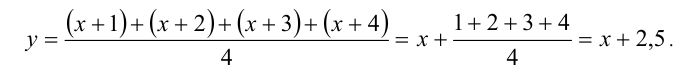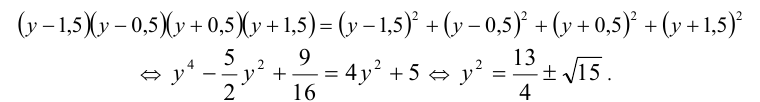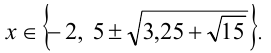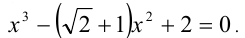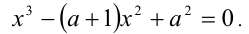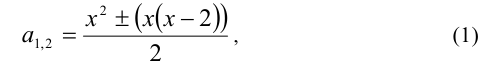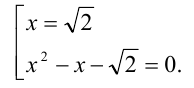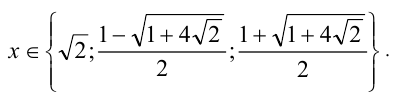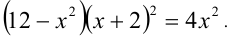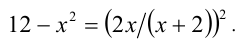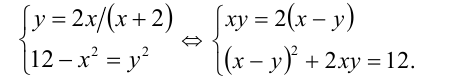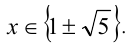- Метод замены переменной – это такой способ решения, при котором в уравнение (или неравенство) вводится новая переменная, в результате чего оно становится более простым.
- Примеры использования метода замены переменной
- Решение уравнений, сводящихся к квадратным
- Биквадратные уравнения
- Метод разложения на множители
- Метод замены переменной
- Выделение полного квадрата
- Примеры
- Метод замены переменных при решении уравнений и неравенств
- Метод замены переменных
- Пример №350.
- Пример №351.
- Пример №352.
- Пример №353.
- Пример №354.
- Пример №355.
- Пример №356.
- 📹 Видео
Метод замены переменной – это такой способ решения, при котором в уравнение (или неравенство) вводится новая переменная, в результате чего оно становится более простым.
Этот метод один из самых популярных при решении сложных заданий, в частности, в ЕГЭ и ОГЭ.
У нас довольно сложное уравнение. А если раскрыть скобки, оно станет еще сложнее. Что делать? Давайте попробуем заменить переменную.
Заменим выражение (x+frac) буквой (t).
Получилось обычное квадратное уравнение! Решив его, найдем чему равно (t), после чего, сделав обратную замену, вычислим (x).
Когда не стоит вводить новую переменную? Когда это не сделает уравнение проще. Например, если старая переменная остается, несмотря на замену:
Попробуем сделать замену здесь.
Заменим выражение (sin x) буквой (t).
Видим, что в этой замене нет никакого смысла – она не упростила уравнение, даже наоборот, усложнила его, потому что теперь у нас в уравнении две переменные.
Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Примеры использования метода замены переменной
Заметим, что (x^4=(x^2 )^2) (см. свойства степеней ). Тогда наше уравнение приобретает следующий вид.
Теперь используем метод замены.
Вводим новую переменную, заменяя (x^2) на (t).
Мы нашли чему равно (t), но найти-то надо иксы! Поэтому делаем обратную замену.
Ответ: (±1); (±) (frac) .
Весьма частая ошибка при использовании этого метода: забыть «вернуться к иксам», то есть не сделать обратную замену. Помните – нам нужно найти (x), а не (t)! Поэтому возврат к (x) — строго обязателен!
Пример. Решить неравенство: (log^2_3x-log_3x-2>0)
Приступим к решению.
Теперь нужно вернуться к исходной переменной – иксу. Для этого перейдем к совокупности , имеющей такое же решение, и сделаем обратную замену.
Видео:Решение уравнения методом замены переменнойСкачать

Решение уравнений, сводящихся к квадратным
Биквадратные уравнения
Биквадратным уравнением называется уравнение вида:
$$ ax^4+bx^2+c = 0, a neq 0 $$
Алгоритм решения биквадратного уравнения
Шаг 1. Ввести новую переменную: $z = x^2 ge 0$.
Переписать уравнение для новой переменной: $az^2+bz+c = 0$
Шаг 2. Решить полученное квадратное уравнение.
Если $D gt 0$, $z_ = frac<-b pm sqrt> $. Проверить условие $z ≥ 0$, если положительных корней нет, решений нет, переход на шаг 4.
Если D = 0,$z_0 = -frac$. Проверить условие $z ge 0$, если корень отрицательный, решений нет, переход на шаг 4.
Если $D lt 0$, решений нет, переход на шаг 4.
Шаг 3.Если после шага 2 остались положительные корни, найти x: $x = pm sqrt$.
Шаг 4. Работа завершена.
Шаг 1. $z = x^2 ge 0, z^2+7z-30 = 0$
$z_1 = -10 lt 0, z_2 = 3 gt 0 $
Шаг 3. Находим корни из положительного $z: x_ = pm sqrt$
Метод разложения на множители
Решение уравнений, в которые переменная x входит с различными натуральными степенями и вещественными коэффициентами, по существу, является поиском корней многочлена.
Число $x_0$ называют корнем многочлена $P_n (x) = a_n x^n+a_ x^ + ⋯ + a_1 x+a_0$ если $P_n (x_0 ) = 0$.
Для многочлена $P_n$ (x) произвольной степени n справедливо следующее.
Если $x = x_0$ является корнем многочлена $P_n$ (x), то $P_n (x) = (x-x_0) P_ (x)$, где $P_ (x)$ — многочлен степени n-1.
Таким образом, разными способами находя корни и формируя скобки, можно постепенно добиваться понижения степени «оставшегося» многочлена, пока не будут найдены все корни.
При разложении многочлена
- множители вида (x-a) называют линейными множителями ;
- множители вида $ (x^2+bx+c)$, для которых $D lt 0$, называют неприводимыми квадратичными множителями .
Любой многочлен $P_n$ (x) можно представить в виде конечного числа линейных и/или неприводимых квадратичных множителей.
Причём, такое представление единственно с точностью до порядка множителей.
Для разложения многочленов на множители применяются разные методы:
- вынесение общего множителя за скобку (см. §19 справочника для 7 класса);
- группировка (см. §20 справочника для 7 класса);
- формулы сокращенного умножения (см. §25 справочника для 7 класса);
- метод неопределённых коэффициентов;
- выделение полного квадрата и т.п.
Решим уравнение $2x^3-x^2-8x+4 = 0$.
Раскладываем на множители: $x^2 (2x-1)-4(2x-1) = 0$
$$ (x^2-4)(2x-1) = 0 Rightarrow (x-2)(x+2)(2x-1) = 0 $$
Корни уравнения: $x_1 = 2, x_2 = -2, x_3 = frac$
Метод замены переменной
Замена переменной – это уравнение, с помощью которого можно упростить исходное уравнение, и перейти к решению системы из двух более простых уравнений:
$Исходное quad сложное quad уравнение iff <left< begin Новая quad переменная quad (урав. quad связи quad со quad старой quad переменной \ Исходное quad урав. quad в quad «упрощ.» quad виде end right.>$
Например, для биквадратных уравнений:
$$ ax^4+bx^2+c = 0 iff <left< begin z = x^2 ge 0 \ az^2+bz+c = 0 end right.> $$
Можно предложить аналогичные схемы для других уравнений:
$$ ax+b sqrt+c = 0 iff <left< begin z = sqrt ge 0 \ az^2+bz+c = 0 end right.> $$
И, в общем виде, для любой рациональной степени n:
$$ ax^+bx^n+c = 0 iff <left< begin z = x^n \ az^2+bz+c = 0 end right.> , n in Bbb Q $$
В других случаях замена переменной не настолько очевидна.
Но при удачном выборе, этот метод очень упрощает задачу.
Раскроем скобки:$ x^2-x = frac$. Сделаем замену:
$$ z = frac Rightarrow z(z-2) = 24 Rightarrow z^2-2z-24 = 0 Rightarrow (z-6)(z+4) = 0 Rightarrow left[ begin z_1 = -4 \ z_2 = 6 end right.$$
Возвращаемся к исходной переменной x:
$$ left[ begin x^2-x = -4 \ x^2-x = 6 end right. Rightarrow left[ begin x^2-x+4 = 0 \ x^2-x-6 = 0 end right. Rightarrow left[ begin D lt 0, x in varnothing \ (x-3)(x+2) = 0 end right. Rightarrow left[ begin x_1 = -2 \ x_2 = 3 end right. $$
При использовании метода замены переменной не забывайте возвращаться к исходной переменной.
Выделение полного квадрата
Метод выделения полного квадрата является одним из методов разложения на множители. Его идея – представить многочлен в виде разности квадратов двух других многочленов степенью пониже, и разложить разность на две скобки:
$$ P_n (x) = Q_k^2 (x)-R_m^2 (x) = (Q_k (x)-R_m (x))(Q_k (x)+R_m (x)) $$
Такое разложение не всегда возможно.
Рассмотрим выделение полного квадрата для квадратного трёхчлена:
$$ = a Biggl(x+frac Biggr)^2 — frac = a Biggl(x+ frac Biggr)^2- frac, D = b^2-4ac $$
Нами выделен полный квадрат $(x+frac)^2$.
Данное выражение используется для построения и анализа графиков парабол (см. §28 данного справочника).
А его разложение на две линейные скобки, известное как теорема Виета (см. §26 данного справочника), возможно только при условии $D ge 0$.
Решить уравнение $x^4+4x^2-1 = 0$
Выделим полный квадрат и разложим на множители:
$$ left[ begin x^2+2-sqrt = 0 \ x^2+2+sqrt = 0 end right. Rightarrow left[ begin x^2 = sqrt -2 gt 0 \ x^2 = -(2+sqrt) lt 0 end right. Rightarrow x_1,2 = pm sqrt<sqrt-2> $$
Примеры
Пример 1. Решите биквадратные уравнения:
Делаем замену: $2x^4+7x^2-4 = 0 iff <left< begin z = x^2 ge 0 \ 2z^2+7z-4 = 0 end right.>$
Решаем квадратное уравнение: $D = 7^2-4 cdot 2 cdot (-4) = 49+32 = 81 = 9^2$
$$ z = frac = left[ begin z_1 = -4 lt 0 \ z_2 = frac gt 0 end right. $$
Выбираем положительный z и возвращаемся к исходной переменной x:
Делаем замену: $(x+3)^4-10(x+3)^2+24 = 0 iff <left< begin z = (x+3)^2 ge 0 \ z^2-10z+24 = 0 end right.>$
Решаем квадратное уравнение: $z^2-10z+24 = 0 Rightarrow (z-4)(z-6) = 0 Rightarrow left[ begin z_1 = 4 \ z_2 = 6 end right.$
Берём оба корня и возвращаемся к исходной переменной.
$$ left[ begin (x+3)^2 = 4 \ (x+3)^2 = 6 end right. Rightarrow left[ begin x+3 = pm sqrt \ x+3 = pm sqrt end right. Rightarrow left[ begin x_ = -3 pm 2 \ x_ = -3 pm sqrt end right. Rightarrow left[ begin x_1 = -5 \ x_2 = -1 \ x_ = -3 pm sqrt end right. $$
Пример 2. Решите уравнения аналогичные биквадратным:
Делаем замену: $x+4 sqrt-60 = 0 iff <left< begin z = sqrt ge 0 \ z^2+4z-60 = 0 end right.>$
Решаем квадратное уравнение: $ z^2+4z-60 = 0 Rightarrow (z+10)(z-6) = 0 Rightarrow left[ begin z_1 = -10 \ z_2 = 6 end right.$
Выбираем положительный корень и возвращаемся к исходной переменной:
Делаем замену: $(x-1)^6-7(x-1)^3-8 = 0 iff <left< begin z = (x-1)^3 \ z^2-7z-8 = 0 end right.>$
Решаем квадратное уравнение: $ z^2-7z-8 = 0 Rightarrow (z+1)(z-8) = 0 Rightarrow left[ begin z_1 = -1 \ z_2 = 8 end right.$
При замене куба знак z может быть любым, берём оба корня и возвращаемся к исходной переменной.
$$ left[ begin (x-1)^3 = -1 \ (x-1)^3 = 8 end right. Rightarrow left[ begin x-1 = -1 \ x-1 = 2 end right. Rightarrow left[ begin x_1 = 0 \ x_2 = 3 end right. $$
Пример 3. Решите уравнения с помощью замены переменной:
Заметим, что $(x+3)^2 = x^2+6x+9$. Получаем:
$$ (x^2+6x)^2-(x^2+6x+9) = 33 Rightarrow (x^2+6x)^2-(x^2+6x)-42 = 0 $$
Решаем квадратное уравнение: $ z^2-z-42 = 0 Rightarrow (z+6)(z-7) = 0 Rightarrow left[ begin z_1 = -6 \ z_2 = 7 end right.$
Берём оба корня и возвращаемся к исходной переменной.
$$ left[ begin x^2+6x = -6 \ x^2+6x = 7 end right. Rightarrow left[ begin x^2+6x+6 = 0 \ x^2+6x-7=0 end right. Rightarrow left[ begin D = 12, x = frac<-6 pm 2 sqrt> \ (x+7)(x-1) = 0 end right. Rightarrow left[ begin x_ = -3 pm sqrt \ x_3 = -7 \ x_4 = 1 end right. $$
Делаем замену: $ frac + frac = 2 iff left[ begin z = x^2+3 ge 3 \ frac + frac = 2 end right.$
Решаем уравнение относительно z:
$$ frac + frac = 2 Rightarrow frac = frac Rightarrow 4(z+1)+5z = 2z(z+1) $$
$$ 2z^2+2z-9z-4 = 0 Rightarrow 2z^2-7z-4 = 0 $$
$$ D = 7^2-4 cdot 2 cdot (-4) = 49+32 = 81 = 9^2 $$
$$ z = frac = left[ begin z_1 = — frac lt 3 \ z_2 = 4 gt 3 end right. $$
Выбираем корень больше 3 и возвращаемся к исходной переменной:
$$ x^2+3 = 4 Rightarrow x^2 = 1 Rightarrow x_ = pm 1$$
Пример 4*. Решите уравнения:
Приведём это уравнение к биквадратному.
В линейных множителях (x+a) выберем все a =
Найдем их среднее арифметическое (см. §52 справочника для 7 класса)
Замена переменных $z = x+a_$:
Упрощаем уравнение, используя формулу разности квадратов:
$$ (z^2-9)(z^2-1) = 945 Rightarrow z^4-10z^2+9 = 945 Rightarrow z^4-10z^2-936 = 0 $$
Получили биквадратное уравнение.
Делаем замену: $z^4-10z^2-936 = 0 iff <left< begin t = z^2 ge 0 \ t^2-10t-936 = 0 end right.> $
Решаем квадратное уравнение:
$$ D = 100+4 cdot 936 = 3844 = 62^2, t = frac = left[ begin t_1 = -26 lt 0 \ t_2 = 36 gt 0 end right. $$
Выбираем положительный корень и возвращаемся к переменной z:
$$ z = pm sqrt = pm sqrt = pm 6 $$
Возвращаемся к исходной переменной x:
$$ x = z-4 = pm 6-4 = left[ begin x_1 = -10 \ x_2 = 2 end right. $$
$$ z- frac =2,1 |times z (z neq 0) $$
$$ z^2-2,1z-1 = 0 Rightarrow D = 2,1^2+4 = 8,41 = 2,9^2; z = frac = left[ begin z_1 = -0,4 \ z_2 = 2,5 end right. $$
Берём оба корня и возвращаемся к исходной переменной.
$$ left[ begin frac = -0,4 \ frac = 2,5 end right. Rightarrow left[ begin x^2+1 = -0,4x \x^2+1 = 2,5x end right. Rightarrow left[ begin x^2+0,4x+1 = 0 \ x^2-2,5x+1 = 0 end right. $$
В первом уравнении $D = 0,4^2-4 lt 0$, решений нет.
Во втором уравнении (x-2)(x-1/2) = 0 $Rightarrow left[ begin x_1 = frac \ x_2 = 2 end right.$
Видео:Решение биквадратных уравнений. 8 класс.Скачать

Метод замены переменных при решении уравнений и неравенств
Метод замены переменных
Этот распространённый метод используется для разных целей: упрощение задачи и повышение её наглядности, придание уравнению (неравенству, системе и проч.) более симметричного вида, сведение одного уравнения к системе нескольких уравнений, рационализация иррациональностей (см. пункт 3.3) и т.д. Иными словами, введение новых переменных производится в тех случаях, когда есть возможность свести задачу к другой, для которой существует более эффективный способ решения.
Существуют виды уравнений, для которых разработаны специальные подстановки, позволяющие наиболее оптимально решать эти уравнения (например, симметрические и возвратные уравнения, однородные уравнения и многие другие). Рассмотрим дополнительно группу примеров, иллюстрирующих различные цели использования этого подхода.
Начнём с примера, в котором при помощи замены неизвестной рациональное неравенство сводится также к рациональному, но более простому алгебраическому неравенству.
Пример №350.
Решение:
Положим 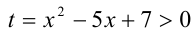
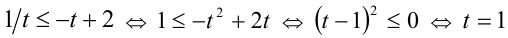
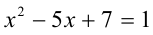
В следующем примере дробно-рациональное уравнение заменой сводится к целому алгебраическому уравнению.
Пример №351.
Решить уравнение
Решение:
Обозначим разность 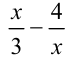
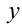
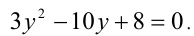
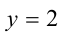
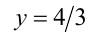
Первое уравнение даёт корни 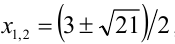
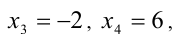
В некоторых случаях алгебраическую задачу (даже если в её условиях не содержится радикалов) с помощью специальных тригонометрических подстановок бывает целесообразно свести к тригонометрической задаче, и далее уже решать её методами тригонометрии.
Пример №352.
Известно, что 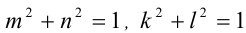
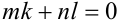
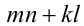
Решение:
Воспользуемся тем, что если два действительных числа X, у удовлетворяют равенству
где 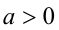
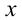
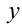
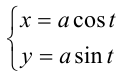
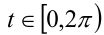
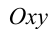
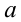
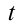
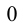
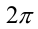
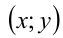
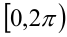
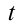
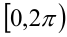
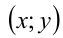
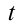
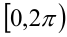
Итак, поскольку числа 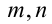
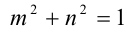
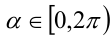
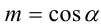
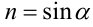
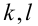
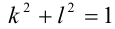
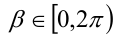
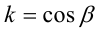
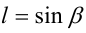
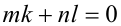
Выполнив тригонометрическую подстановку в искомом выражении 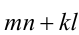
Введение новых переменных может быть вызвано необходимостью понизить степень уравнения, упростив при этом решение задачи.
Пример №353.
Решить уравнение
Решение:
Сведём данное уравнение 4-й степени к квадратному уравнению. Для этого вначале умножим обе части уравнения на 12 и приведём его к виду
Затем сделаем подстановку 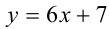
Сделав ещё одну подстановку 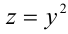
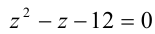
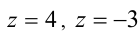
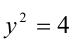
Ответ:
В следующем примере используется симметризирующая подстановка. Название говорит само за себя: уравнению придаётся более «симметричный» вид. Новая переменная является средним арифметическим входящих в уравнение выражений. При её применении уравнение 4-й степени общего вида приводится к более простому частному случаю, а именно, симметризация уравнения позволяет «убрать» из уравнения нечётные степени неизвестной, оставив только чётные и превратив его, таким образом, в биквадратное уравнение.
Пример №354.
Решение:
Выполним симметризирующую подстановку
Тогда уравнение примет вид
Ответ:
6.Близко к методу введения новых переменных стоит так называемый метод введения параметра. Не всегда введение параметра усложняет задачу. На примере, рассмотренном ниже, видно, как включение параметра в уравнение вместо числового коэффициента позволяет лучше «разглядеть» способ дальнейшего его решения — рассмотрение уравнения как квадратного относительно введённой величины.
Пример №355.
Решение:
Введём в уравнение параметр, положив 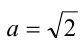
Рассмотрим теперь это уравнение как квадратное относительно 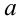
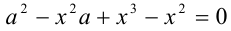
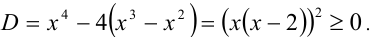
т.е. 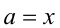
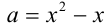
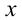
Заменяя 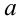
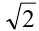
Отсюда находим решения:
Замечание. В формуле корней квадратного уравнения более корректным было, вообще говоря, написать
Однако когда ищутся оба корня, то использование формул (1) и (2) приводит к одному результату. Именно поэтому часто в подобных ситуациях модуль опускают.
7.Отметим, что, вообще говоря, не всегда в задаче нужно полностью переходить к новым переменным. Иногда имеет смысл, вводя новую переменную, сохранить в задаче и первоначальную переменную, т.е. сделать частичную замену переменных. Так, сведением к системе уравнений, решаются некоторые уравнения. Рассмотрим в качестве пояснения пример.
Пример №356.
Решение:
Так как 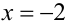
Положим 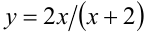
Решая эту систему относительно 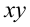
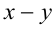
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
📹 Видео
9 класс, 11 урок, Методы решения систем уравненийСкачать

9 класс. Алгебра. Решение уравнений методом замены переменной.Скачать

Алгебра 9 класс. Решение систем уравнений методом замены переменныхСкачать

Решение квадратных уравнений. Метод разложения на множители. 8 класс.Скачать

Алгебра Система уравнений Метод замены переменной № 6.22 9 классСкачать

Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

#139 Урок 64. Решение уравнений методом замены. Как понизить степень уравнения заменив переменную?Скачать

Решение систем уравнений методом подстановкиСкачать

Быстрый способ решения квадратного уравненияСкачать

Решение систем уравнений второго порядка. 8 класс.Скачать

ПОСМОТРИ это видео, если хочешь решить систему линейных уравнений! Метод ПодстановкиСкачать

Решение квадратного уравнения методом замены переменнойСкачать

КАК РЕШАТЬ КУБИЧЕСКИЕ УРАВНЕНИЯ | Разбираем на конкретном примереСкачать

Решение систем уравнений методом подстановки (с решением квадратных уравнений). Алгебра 9 класс.Скачать

Дробно-рациональные уравнения. 8 класс.Скачать

Пример 47. Решить систему методом замены переменнойСкачать

Как решать квадратные уравнения без дискриминантаСкачать