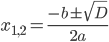Квадратное уравнение ax 2 + bx + c = 0 на C++ лучше всего решать с помощью формулы, содержащей дискриминант:
Разберем пример кода такой программы:
Данная программа учитывает все исходы при решении подобного уравнения.
- Похожие записи:
- Квадратное уравнение: 8 комментариев
- Программирование на Паскале. Тема: «Решение квадратного уравнения с использованием конструкции IF–THEN–ELSE»
- Программа для решения квадратных уравнений на C++
- Алгоритм решения квадратного уравнения
- Для вас это может быть интересно:
- Программа для решения квадратных уравнений на C++ : 24 комментария
- Добавить комментарий Отменить ответ
- 🌟 Видео
Похожие записи:
Видео:5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

Квадратное уравнение: 8 комментариев
Добрый день! А как быть со случаями, когда а == 0; b == 0 && c > 0; b == 0 && C !=0 и т.д.?
При a == 0 уравнение перестает называться квадратным. Проблемы также возникают, когда, например, пользователь ввел букву вместо числа. Такие случаи называются аномалиями.
Все аномалии рассмотреть нельзя. Если требуется, то можно, например, рассмотреть аномалию a == 0, добавив после 11-й строки:
if (a == 0)
<
cout
«Все аномалии рассмотреть нельзя.»
Сложно с Вами согласиться. Не такая уж это и нетривиальная задача для программиста — решить уравнение ax2 + bx + c = 0 на C++, учтя все возможные варианты а, b, c, в том числе и когда уравнение перестает быть квадратным и другие.
В противном случае код получается не универсальный, а только для некоторых случаев, когда переменные Вас «устраивают».
Согласитесь — это не решение задачи, а нахождение решения для группы частных случаев.
Нельзя. Будет всегда компьютер, бракованный, на котором программа не будет работать. На этом факте основано всё лицензирование программного обеспечения. Бракованный компьютер — тоже совокупность аномалий.
По квадратному уравнению имеет смысл рассматривать аномалии только, если от Вас это требуется в задании. И процесс такой длительный:
1. Рассматриваются случаи, когда пользователь ввел уравнение, не являющееся квадратным.
2. Рассматриваются случаи, когда пользователь ввел a,b,c, не являющиеся числами.
3. Рассматриваются случаи, когда пользователь, не умеет запускать программу, пишется инструкция.
4. Рассматриваются случаи, когда пользователь не умеет читать, пишется инструкция с картинками, часто с голосовым помощником.
5. Это именно программа, поэтому можно также составить инструкцию по компиляции, указать различные версии программы для разных стандартов языка.
.
Это все не моя выдумка, так делают, но только, если это действительно нужно.
Бывает другой случай, например, нужно сдать программу, решающую квадратное уравнение, преподавателю и вот здесь нужно сделать минимум, то, что написано в примере, а дальше, только если преподаватель просит.
Нет. Вы не правы.
Про аномалии — я вообще ничего не говорю. Я говорю только про задачу, которую озвучили Вы: решить ax2 + bx + c = 0. Другими словами — найти все возможные ответы при абсолютно любых значениях а, b и с. Без исключений. Не важно — квадратное будет уравнение или линейное, после того, как мы с консоли введем переменные. В этом весь смысл программирования. Сделать универсальное решение, которое будет работать всегда, при любых значениях переменных (аномалии, когда пользователю оторвало руки и он не может ввести переменные с консоли, истекая кровью, я тоже не рассматриваю).
Глупо, имея инструмент, который позволяет решить задачу, не решать её в любых, без исключения, случаях. А ограничивать себя только удобными случаями и тривиальными. Это не программирование получается, а ерунда какая-то, решение частных случаев. «Сюда — смотри, сюда — не смотри, а здесь — рыбу заворачивали. »
Вот, корявый, конечно, не оптимальный, но работающий во всех случаях код:
#include
#include
using namespace std;
int main() <
double a, b, c;
cin >> a >> b >> c;
/*(D = b*b minus 4*a*c) — считаем дискриминант*/
double d = (b*b) — 4 * a * c;
double x1, x2, d1;
d1=sqrt(d);/*корень из дискриминанта — заготовка для решения решаемого квадратного уравнения*/
/*1. группируем все исключения — когда решение вообще или через дискриминант невозможно*/
/*2. в каждое исключение сливаем все условия и для этих условий пишем вывод*/
/*3. оставшиеся случаи решаем через дискриминант*/
if ((a==0 && b == 0 ) || ( b==0 && ((c> 0 && a>0) || (c
Про аномалии это я переделал. Лучше говорить аномалии, а не исключения.
Задачу читайте внимательно: квадратное уравнение. Подразумевается, что коэффициент a не равен 0.
Посмотрите математическую энциклопедию.
Ещё раз повторю: Вы не сможете сделать универсальное решение, которое будет работать всегда.
Ваше решение просто лучше моего, оно не работает, если вместо a, я ввожу rrr или другие символы.
Аномалии про оторванные руки и кровь тоже рассматривают, есть даже задачи и модели математические про ситуацию, когда 0 взял так и случайно стал 1 в памяти ЭВМ. Про глупость, ну а что, так и есть, глупость это нормально. Ваша программа умнее моей.
Это не ерунда, а программирование. Первый этап, который всегда должен происходить, это спецификация (уточнение) задачи. Пишется такая бумага, в которой как раз и есть «Сюда — смотри, сюда — не смотри, а здесь — рыбу заворачивали. «.
Вопрос у Вас фактически про спецификацию (уточнение). Те пять пунктов, которые я в предыдущем комментарии написал — совершенно адекватные требования преподавателя, заказчика, сайта с хранилищем программного обеспечения. Часто преподаватели говорят — составить отчёт с инструкциями даже по такой программе как решение квадратного уравнения, это нормально. Про оторванные руки я не писал как раз как про первоочередную задачу.
Но по минимуму решение именно то, что я написал. Оно, бывает, проходит, при быстром ответе на вопрос экзамена. Если требуют уточнить, нужно уметь уточнять. Да и ещё раз замечу, Ваше решение умнее моего, но оно не универсально.
Математической энциклопедии под рукой не нашлось.
«Лучше говорить аномалии, а не исключения.»
Не помню из курса алгебры (в рамках которой изучается решение квадратных уравнений) такого термина — аномалии, но допускаю, что Вы правы и такой математический термин существует и его можно применить к квадратному уравнению.
«Задачу читайте внимательно: квадратное уравнение. Подразумевается, что коэффициент a не равен 0.»
Прочитал внимательно. «ax2 + bx + c = 0» — где сказано, что а не равен нулю?
«Но по минимуму решение именно то, что я написал. Оно, бывает, проходит, при быстром ответе на вопрос экзамена.»
Когда я пытался пропихнуть код, который не учитывает исключений — не приняли, хотя вот текст моего задания:
«На вход вашей программы в стандартном потоке ввода подаются действительные коэффициенты A, B и C уравнения Ax² + Bx + C = 0. Выведите все его различные действительные корни в поток вывода в любом порядке, при этом разделяя корни пробелами. Гарантируется, что хотя бы один из коэффициентов уравнения не равен нулю.»
«Вы не сможете сделать универсальное решение, которое будет работать всегда.» и «Да и ещё раз замечу, Ваше решение умнее моего, но оно не универсально.»
Позвольте, Вы настаиваете, что невозможно написать код, который будет решать квадратное уравнение при любых действительных a, b и c? Как-то можете теоретически аргументировать? Пока что только не подкрепленные утверждения, не готов принимать их на веру.
При каких действительных значениях а, b и c мой, реально корявый, код не работает?
Страницы математических энциклопедий доступны через Яндекс. Только внимательнее, там есть поясняющие материалы в результатах поиска, не перепутайте.
Квадратное уравнение — алгебраическое уравнение 2-й степени. Общий вид К. у. ax^+bx+c=0, a != 0.
Что такое аномалия?
В тестировании программного обеспечения под аномалией понимается результат, отличный от ожидаемого. Такое поведение может быть результатом документа а также представлений и опыта тестировщиков.
Аномалия может также относиться к проблеме удобства использования, поскольку тестовое программное обеспечение может вести себя в соответствии со спецификацией, но удобство его использования все же можно улучшить. Иногда аномалия также может быть названа дефектом / ошибкой.
Перед тем как разрабатывать программу проводят формальную спецификацию (уточнение) задания.
В информатике формальная спецификация — это математическое описание программной или аппаратной системы, которая может быть реализована в соответствии с этим описанием. Специфицируется, что должна делать система, но не то, как она должна это делать.
Если система огромная — длительное обсуждение, анализ и т.д. Для небольших программ, вот как решение квадратного уравнения, можно на бумаге составить. Вот на этой бумаге пишется задача, ИД — исходные данные, ВД — выходные данные, реакция на аномалии и т.д. В пункте реакция на аномалии рисуется таблица, по крайней мере с двумя столбцами: название аномалии, то что программа будет в этом случае делать.
У Вас в задании слова квадратное как раз нет и аккуратно написано, что подаются только действительные числа. Формальная спецификация выполнена в задании в основном.
Если будут вводить только действительные числа, можно написать работающий код. По такой формальной спецификации можно, я почти уверен, хотя доказательства корректности работы программы трудные.
Нельзя написать универсальное решение, без аномалий, на все случаи жизни. Тот же потенциальный пользователь программы решения квадратного уравнения, школьник, будет тыкать во всю клавиатуру, а не только в цифры.
Видео:решение (поиск корней) квадратных уравнений c++Скачать

Программирование на Паскале. Тема: «Решение квадратного уравнения с использованием конструкции IF–THEN–ELSE»
Цели урока:
Оборудование:
До сих пор мы с вами говорили о каких-то отвлечённых задачах из области математики. Сегодня мы поговорим о конкретной задаче, которая встречается у вас почти на каждом уроке. Это решение квадратного уравнения. Я хочу, чтобы вы на примере этой задачи поняли, что программирование — это не просто прихоть учителя, это действительно раздел информатики, который может нам помочь, например, в решении конкретных математических задач. Нужно только уметь разбираться в этом.
2. Математическое решение
Давайте вспомним, что понимают под квадратным уравнением?
Что из себя представляют числа a,b,c и как их называют?
С чего начинают решение квадратного уравнения?
Найдите вокруг себя формулу дискриминанта. (D=b 2 -4ac) (Приложение 3)
Как мы решаем далее квадратное уравнение? (сравнение D с нулём)
Какие выводы мы из этого делаем?
(если D 0, то два корня)
Как найти корни квадратного уравнения? Найдите формулы корней среди тех, что развешены повсюду.
Если я случай наличия корней квадратного уравнения сведу к условию D
(Два одинаковых корня)
Давайте ещё раз подробно разберём нашу задачу:
Итак, у нас есть квадратное уравнение ax 2 +bx+c=0.
Мы должны решить его, т.е. найти такие значения х, при которых правая часть уравнения =0. Мы знаем, что для этого нам надо:
Найти дискриминант D=b 2 — 4ac.
Сравнить его с нулём
D=b 2 -4ac=10 2 -4*3*3=100 — 36 =64
Х1=
X2 =
3. Составление блок-схемы алгоритма.
По заданному решению попробуем составить блок-схему алгоритма в тетради. Кто справится первым, прошу к доске.
Подпишем основные элементы блок — схемы применительно к языку программирования.
4. Составление программы по блок — схеме.
Теперь, пользуясь нашими записями, составим программу и покажем её учителю. Тот, кто до конца урока составит только программу, не проверив её на компьютере, получит три, тот, кто наберёт программу на компьютере, но не проверит её на примерах, получит три. Тот, кто выполнит всё задание, получит пять.
А я раздам вам домашнее задание.
Var a,b,c,d,x1,x1: real;
Write(‘введите коэффициенты уравнения a,b,c’); readln(a,b,c);
Else writeln(‘действительных корней нет’)
1. Составить и набрать программу КВУР на компьютере.
Загрузка среды Pascal- 2ЩЛКМ по значку Pascal, нажать ALT+ENTER.
Запуск программы — ЩЛКМ по кнопке RUN выбрать RUN.
2. Решить следующие квадратные уравнения и показать учителю их решения (если нет такой возможности, то занести их в маршрутный лист (Приложение 4)
1,5х 2 -0,6х — 4,8 = 0
3. Переделайте программу КВУР таким образом, чтобы в ней учитывался случай, когда D=0 и уравнение имеет один корень.
4. Закрыть программу.
Подсказка: Меню File — Exit или ALT+X.
1. За простое воспроизведение (набор программы) без проверки оценка «3»
2. За проверку работы программы на примерах, представленных учителем оценка «4»
3. За решение всех заданий и дополнительное изменение программы для случая D=0, оценка «5»
4. Закрыть программу.
Подсказка: Меню File — Exit или ALT+X.
| № | Х1 | Х2 |
| 1 | 3,230139 | 0,1031947 |
| 2 | 1,464102 | -5,464102 |
| 3 | 1,106107 | -1,356107 |
| 4 | Корней нет | |
| 5 | Корней нет | |
| 6 | 1,6 | 0 |
| 7 | 2 | -1,6 |
| 8 | Корней нет | |
| 9 | 0,6872614 | -1,131706 |
| 10 | 9,486833 | -9,486833 |
Можно дать дополнительное задание:
Изменить программу так, чтобы ответ был с точностью до 2-х знаков после запятой.
1) Напишите программу проверки пароля. Пусть пароль — некоторое число, зафиксированное в программе. Программа печатает приглашение «введите пароль» и вводит число. Если введённое число совпадает с фиксированным паролем, то программа выводит приветствие, если нет — сообщает о том, что пароль не угадан.
7. Подведение итогов урока.
Итак, ребята, сегодня мы с вами решали конкретные задачи из математики, применяя свои умения по программированию. Вы получили следующие оценки за свои знания. (Перечисление оценок) На следующем уроке нам предстоит познакомиться с новыми алгоритмами — Циклическими.
На сегодня наш урок закончен. До свидания.
Литература:
Видео:34 Задача: Найти корни квадратного уравнения при помощи PythonСкачать

Программа для решения квадратных уравнений на C++

Алгоритм решения квадратного уравнения
Многие знают, что уравнение вида ax 2 + bx + c = 0 , где a не равно 0, называют квадратным уравнением.
Существуют различные способы решения квадратных уравнений, но мы рассмотрим решение через дискриминант.
Обозначается дискриминант буквой D . Из школьного курса знаем, что D = b 2 — 4ac .
Существует несколько условий:
- Если D > 0, то решение имеет 2 различных вещественных корня.
- Если D = 0, то оба вещественных корня равны.
- Если D для вводавывода в консоли, #include для работы с математическими функциями и область using namespace std;
Просим пользователя ввести значения переменных и сохраняем каждое значение
Проверяем условие, если дискриминант больше или равен 0, то находим корни и выводим
в противном случае выводим сообщение
На этом всё, осталось скомпилировать, запустить и проверить. Запускаем и вводим данные, чтобы D был меньше 0
В этом случае D = 3*3 — 4*2*3 = -15, а это меньше 0, значит ответ программа дала верный.
Ответы тоже верны. Программа работает правильно.
Ниже представлен весь листинг программы для нахождения корней квадратного уравнения на C++
Для вас это может быть интересно:
Видео:Квадратные уравнения от «А» до «Я». Классификация, решение и теорема Виета | МатематикаСкачать

Программа для решения квадратных уравнений на C++ : 24 комментария
Программировать так сложно…
- Nicknixer Автор записи 15.10.2016
Не так сложно, как Вам кажется! Немного литературы, немного практики и смотреть на код решения такой задачи Вы будете по-другому.
Доброго времени суток! Помогите пожалуйста написать программу, которая считает сколько символов в ряде двумерного массива. То есть , например массив 5 на 5, сколько символов в 1 ряде, сколько во 2 и т.д.
Ответил вам по электронной почте
Критику принимаете? 🙂
Программа дырявая как сито.
Если число очень маленькое, но положительное, например 10^(-20) — у вас будет переполнение или типо того. Оператор > проверяет знак числа (это отдельный бит), а оператор == для дробных чисел не имеет смысла, т.к. в младших разрядах числа обычно находится какой-нибудь мусор, который при таком сравнении дает false.
x = ( -1*b + sqrt(b*b — 4*a*c) ) / (2 * a);
x = ( -1*b — sqrt(b*b — 4*a*c) ) / (2 * a);
Тут есть три вопроса:
1) зачем два раза вычислять одно и тоже (я про корень)
2) что делать если мне корни надо как-то использовать, а не просто вывести (тут есть проблема, ведь у меня то один корень — то два). Чтобы лучше понять в чем проблема — попробуйте вынести вычисление корней в отдельную функцию. У вас то вообще, если корень один — то их выведется все равно два, одинаковых.
3) в переменной «a» может быть ноль (или близкое к нулю число) — при этом мы получим деление на ноль (а точнее, переполнение).
Но это ведь еще не все. Что будет если и «a» и «b» равны нулю? — тебе надо рассмотреть два варианта — если c = 0 (условно, близко к нулю), то корней бесконечно много. А если c != 0, то корней нет.
Вообще, эта задача — прекрасный пример для юнит-тестирования и демонстрации принципов разработки через тестирование. Именно его я рассматривал в своей статье по теме тестирования: Юнит-тестирование. Пример. Boost Unit Test. Дело в том, что тут куча вариантов сделать ошибку, при этом их понимание приходит не сразу, т.е. школьник решая задачу напишет по формуле которой учили (ну и вот как у вас). А потом надо разбираться и смотреть как программа может сломаться, при этом разрабатывать тесты.
- Николай Сергейчук Автор записи 09.02.2017
Принимаем 🙂
Согласен с вами во всём! Программу можно реализовать намного лучше, используя различные проверки и валидацию входных данных.
Однако, статья рассчитана на аудиторию, которая только начинает познавать программирование или делает лабораторную. 🙂 Чтобы людям легче было понять, реализация данной программы упрощена до невозможности. И, возможно, несправедливо было с моей стороны не предупредить их о возможных ошибках в работе программы, которые могут вскрыться позже, если подать на вход определенные значения.
Кстати, у вас интересная статья по тестированию!
Николай, доброго времени суток! Можете помочь с написанием програмки в с++? 1-1/2!+1/3!-1/4!+1/5! и так до 1/100! ? Чтобы при заднии в строке номера члена последовательности выдавал сумму до него по такой вот формуле? Буду очень благодарен!
Пожалуйста подскажите как ввести экран правильный ответ дискриминанта
Помогите решить в Dev C++
Sqrt x^2+1+sqrt|x|,x0
Здравствуйте, можете помочь с решением биквадратного и триквадратного уравнения?
#include
using namespace std;
int main()
<
/*Решение квадратных уравнений*/
setlocale(0, «»);
cout a;
cout b;
cout c;
D = pow(b, 2) — 4 * a * c;
cout
ну и? если даже тупо скопировать код и вставить его в cpp.sh , ничего не работает. поебота какая то этот с++
Уважаемая, Лена! Я, надеюсь, вы знаете, что код программы, написанной на языке программирования C++ нельзя тупо вставить в блокнот и сохранить под названием «cpp.sh»? Если не знали, то я, видимо, открыл для вас Америку!
помогите решить. заданы 3 перемены a.b.c записать вы радение на С
< 7a/b+2a, если a=b,
Х= b,
b и а не равно != с
iconcerts где забыл
#include
Я ради интереса написал программу нахождения корней квадратного уравнения на С++, с выводом корней как в десятичном виде, так и в виде простой дроби (причём уже сокращённой), потому что выводя корни в десятичном виде программа их одновременно сокращает и округляет и 1/3 превращается в 0.333333 хотя на самом деле 0.333333 (3), то есть для проверки правильно ли нашёл корни ваш ребёнок, вы с получите что-то типа: X1= 0.285714; X2=0.214286, а на самом деле это будет X1=2/7; X2=3/14, кроме того, если корень из дискриминанта не получается целым числом, вы уже получите двойную неточность: сначала при извлечении корня программа отсечёт значение до 4-6 цифр после запятой с округлением, а затем сделает то же самое при делении числителя на знаменатель. Я и здесь сделал вывод корней в двух значениях: в десятичном и в виде выражения X1= (-b + sqrt(D))/(2*a); X2= (-b — sqrt(D))/(2*a), то есть выводится примерно вот так X1=-5+sqrt(21)/2; X2=-5-sqrt(21)/2 с одновременным разложением дискриминанта под корнем на множители, вынесением этих множителей из-под корня, если они выносятся нацело, их перемножением и дальнейшим сокращением. Вот, например, имеем a=3, b=15, c=3, при решении получаем D=189 программа выдаёт десятичные корни X1= -0.208712 и X2= -4.79129, а в виде выражения имеем: X1= -5+sqrt(21)/2, то есть первоначально получаем: X1= -15+sqrt(189)/6, -> 189=21*9 -> -15+3sqrt(21)/6 далее идёт сокращение на 3 и итог -5+sqrt(21)/2
День добрый.
Недавно начал изучать C++. Решил попробовать написать решение квадратного уравнения именно через оператор вида «условие ? выполняется : не выполняется». Т.е. если условие выполняется, то имеем два решения (даже если d = 0, то тоже должно быть два решения x1 = x2), если d a;
std::cout b;
std::cout c;
d = pow(b, 2) — 4 * a*c;
d >= 0 ? xfst = ((-b + sqrt(d)) / double(2 * a)) , xscd = ((-b — sqrt(d)) / double(2 * a)) : std::cout
- Николай Сергейчук Автор записи 12.02.2020
if (d >= 0) <
xfst = ((-b + sqrt(d)) / double(2 * a));
xscd = ((-b — sqrt(d)) / double(2 * a));
std::cout
Создать программу для решения квадратного уравнения.
У меня не получаеться, но и копифейсом я не хочу заниматься.
Прошу помогите. Заранее спасибо.
Здравствуйте! Как решить эту задачу? Приведенный пример сверху не подходит .
Давайте напишем действительно полезную программу! Вы наверняка уже устали считать дискриминант для квадратных уравнений? Давайте автоматизируем этот процесс.
На вход программы подаются три целых числа — коэффициенты уравнения ax^2 + bx + c = 0ax
2
+bx+c=0
Гарантируется, что a neq 0a
=0.
Выведите через пробел корни уравнения в порядке убывания и округленные «вниз». Если уравнение имеет корень кратности 2 — выведите одно число. Если у уравнения нет действительных корней — выведите «NO»
Для извлечения корней используйте функцию sqrt. Она содержится в библиотеке сmath ( она уже импортирована в коде ). Для округления воспользуйтесь функцией floor ( из той же библиотеки ).
1 0 -4
Sample Output 1:
2 -2
Sample Input 2:
1 2 2
Sample Output 2:
Пожалуйста подскажите как ввести экран ответ дискриминанта
Пожалуйста подскажите как ввести на екран ответь дискриминанта
Подскажите как правильно решить?
Обчислити z = (x1 + y1) / (x2 + y2), де х1, х2 — коренi рiвняння 2х^2 + x — 4 =0.
y1, y2 — коренi рiвняння ay^2 + 2y — 1 = 0. Усi коренi дiйснi.
using namespace std;
int main() <
double a = 2, b, c = -4;
int x1, x2;
double a1, b1 = 2, c1 = -1;
int y1, y2;
float z;
if((b*b — 4*a*c) >= 0 ) <
x1 = ( -1*b + sqrt(b*b — 4*a*c)) / (2 * a);
cout a1;
if((b1*b1 — 4*a1*c1) >= 0) <
y1 = ( -1*b1 + sqrt(b1*b1 — 4*a1*c1)) / (2 * a1);
cout = 0, y1 >= 0, y2 >= 0) <
z = (x1 + y1)/(x2 +y2);
cout
Добавить комментарий Отменить ответ
Этот сайт использует Akismet для борьбы со спамом. Узнайте, как обрабатываются ваши данные комментариев.
🌟 Видео
Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

Программа для решения квадратных уравнений на С++Скачать

решаем квадратные уравнения в ExcelСкачать

Программа для решения корней квадратного уравнения с использованием дискриминанта на языке ПаскальСкачать
Решение биквадратных уравнений. 8 класс.Скачать

Задача 411. Квадратное уравнение. acmp.ru C++Скачать

Пишем программы #1 квадратные уравнения на C++Скачать

Программа, определяющая корни квадратного уравнения. Язык программирования Python.Скачать

Как решать квадратные уравнения. 8 класс. Вебинар | МатематикаСкачать

Алгебра 8 класс (Урок№30 - Решение приведённых квадратных уравнений. Теорема Виета.)Скачать

Решение задач с помощью квадратных уравнений. Алгебра, 8 классСкачать

Алгебра 8. Урок 9 - Квадратные уравнения. Полные и неполныеСкачать

С++ 03 03. Находим корни квадратного уравнения.Скачать

Неполные квадратные уравнения. Алгебра, 8 классСкачать

Формула корней квадратного уравнения. Алгебра, 8 классСкачать

Представление моей программы по нахождению дискриминанта и корней квадратных уравненийСкачать