В данной статье мы расскажем о матричном методе решения системы линейных алгебраических уравнений, найдем его определение и приведем примеры решения.
Метод обратной матрицы — это метод, использующийся при решении СЛАУ в том случае, если число неизвестных равняется числу уравнений.
Найти решение системы n линейных уравнений с n неизвестными:
a 11 x 1 + a 12 x 2 + . . . + a 1 n x n = b 1 a n 1 x 1 + a n 2 x 2 + . . . + a n n x n = b n
Матричный вид записи: А × X = B
где А = а 11 а 12 ⋯ а 1 n а 21 а 22 ⋯ а 2 n ⋯ ⋯ ⋯ ⋯ а n 1 а n 2 ⋯ а n n — матрица системы.
X = x 1 x 2 ⋮ x n — столбец неизвестных,
B = b 1 b 2 ⋮ b n — столбец свободных коэффициентов.
Из уравнения, которое мы получили, необходимо выразить X . Для этого нужно умножить обе части матричного уравнения слева на A — 1 :
A — 1 × A × X = A — 1 × B .
Так как А — 1 × А = Е , то Е × X = А — 1 × В или X = А — 1 × В .
Обратная матрица к матрице А имеет право на существование только, если выполняется условие d e t A н е р а в е н н у л ю . Поэтому при решении СЛАУ методом обратной матрицы, в первую очередь находится d e t А .
В том случае, если d e t A н е р а в е н н у л ю , у системы имеется только один вариант решения: при помощи метода обратной матрицы. Если d e t А = 0 , то систему нельзя решить данным методом.
Видео:Матричный метод решения систем уравненийСкачать

Пример решения системы линейных уравнений с помощью метода обратной матрицы
Решаем СЛАУ методом обратной матрицы:
2 x 1 — 4 x 2 + 3 x 3 = 1 x 1 — 2 x 2 + 4 x 3 = 3 3 x 1 — x 2 + 5 x 3 = 2
- Записываем систему в виде матричного уравнения А X = B , где
А = 2 — 4 3 1 — 2 4 3 — 1 5 , X = x 1 x 2 x 3 , B = 1 3 2 .
- Выражаем из этого уравнения X :
- Находим определитель матрицы А :
d e t A = 2 — 4 3 1 — 2 4 3 — 1 5 = 2 × ( — 2 ) × 5 + 3 × ( — 4 ) × 4 + 3 × ( — 1 ) × 1 — 3 × ( — 2 ) × 3 — — 1 × ( — 4 ) × 5 — 2 × 4 — ( — 1 ) = — 20 — 48 — 3 + 18 + 20 + 8 = — 25
d e t А не равняется 0, следовательно, для этой системы подходит метод решения обратной матрицей.
- Находим обратную матрицу А — 1 при помощи союзной матрицы. Вычисляем алгебраические дополнения А i j к соответствующим элементам матрицы А :
А 11 = ( — 1 ) ( 1 + 1 ) — 2 4 — 1 5 = — 10 + 4 = — 6 ,
А 12 = ( — 1 ) 1 + 2 1 4 3 5 = — ( 5 — 12 ) = 7 ,
А 13 = ( — 1 ) 1 + 3 1 — 2 3 — 1 = — 1 + 6 = 5 ,
А 21 = ( — 1 ) 2 + 1 — 4 3 — 1 5 = — ( — 20 + 3 ) = 17 ,
А 22 = ( — 1 ) 2 + 2 2 3 3 5 — 10 — 9 = 1 ,
А 23 = ( — 1 ) 2 + 3 2 — 4 3 — 1 = — ( — 2 + 12 ) = — 10 ,
А 31 = ( — 1 ) 3 + 1 — 4 3 — 2 4 = — 16 + 6 = — 10 ,
А 32 = ( — 1 ) 3 + 2 2 3 1 4 = — ( 8 — 3 ) = — 5 ,
А 33 = ( — 1 ) 3 + 3 2 — 4 1 — 2 = — 4 + 4 = 0 .
- Записываем союзную матрицу А * , которая составлена из алгебраических дополнений матрицы А :
А * = — 6 7 5 17 1 — 10 — 10 — 5 0
- Записываем обратную матрицу согласно формуле:
A — 1 = 1 d e t A ( A * ) T : А — 1 = — 1 25 — 6 17 — 10 7 1 — 5 5 — 10 0 ,
- Умножаем обратную матрицу А — 1 на столбец свободных членов В и получаем решение системы:
X = A — 1 × B = — 1 25 — 6 17 — 10 7 1 — 5 5 — 10 0 1 3 2 = — 1 25 — 6 + 51 — 20 7 + 3 — 10 5 — 30 + 0 = — 1 0 1
Ответ: x 1 = — 1 ; x 2 = 0 ; x 3 = 1
Видео:Решение матричных уравненийСкачать

Квадратичные формы
Содержание:
Видео:5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

Квадратичные формы и их определение
Определение. Квадратичной формой L (x1, x2, . xn) от n переменных называется сумма, каждый член которой является или квадратом одной из переменных, или произведением двух различных переменных, взятых с некоторым коэффициентом, то есть

Допускаем, что в квадратичной форме (2.44) aij — действительные числа. Распишем квадратичную форму (2.44), разбив слагаемые, содержащие произведения переменных, на две равные части:
Матрица

или A = <aij> (i, j = 1, 2, . n) является симметричной, так как aij = aji, называется матрицей квадратичной формы (2.44).
Рангом квадратичной формы называется ранг ее матрицы. Квадратичная форма называется невырожденной, если ее матрица невырожденная.
Если 
Выражение X T AX представляет собой квадратичную форму в матричном виде.
Пример 1. Записать в матричном виде квадратичную форму
Решение. Матрица данной квадратичной формы имеет вид
А =
Значит, 
Квадратичная форма называется канонической (или другими словами, имеет канонический вид), если все aij = 0, когда i ≠ j. Тогда квадратичная форма будет иметь вид 
Рассмотрим следующую теорему.
ТЕОРЕМА 1. Произвольная квадратичная форма приводится к каноническому виду.
Доказательство. Пусть задана квадратичная форма (2.44) с матрицей (2.45) в базисе 

Матрица B является матрицей перехода от базиса

к некоторому базису 
Примечание. Действительная квадратная матрица называется ортогональной, если сумма квадратов элементов каждого столбца равна единице и сумма произведений соответствующих элементов из двух разных столбцов равна нулю. Необходимое и достаточное условие ортогональности матрицы В является условие В T ⋅ B = Е.
Пусть X и Y являются векторами-столбцами из координат вектора 

или

Примечание. При доказательстве данной теоремы использовали транспонирование произведения матриц по формуле (СY) T = Y T ⋅ C T .
Заметим, что в канонической форме (2.48) λ1, λ2, . λn являются собственными числами матрицы A.
Пример 2. Привести квадратичную форму 
Решение. Матрица данной квадратичной формы имеет вид 

Характеристическое уравнение данной системы имеет вид

Решив данное уравнение, находим λ1 = 6, λ2 = 1. Значит канонический вид данной квадратичной формы является 
Найдем ортогональную матрицу.
Столбцами ортогональной матрицы, которая приводит квадратичную форму к каноническому виду, является ортонормированный собственные вектор-столбец матрицы A.
Сначала найдем нормированный собственный вектор-столбец матрицы A с собственным значением λ1 = 6. Для этого из системы (2.49) имеем систему для нахождения координат вектора: 
Из данной системы находим x2 = 2x1 или u2 = 2u1. Значит, при произвольном u1, отличном от нуля, столбец 


Аналогично находим вектор-столбец матрицы A с собственным значением λ2 = 1, а именно из системы: 
Находим x1 = –2x2 или при произвольном s, отличном от нуля, столбец 


Замечание. Легко проверить, что 
Рассмотрим на примере еще один метод приведения квадратичной формы к каноническому виду.
Метод Лагранжа приведения квадратичной формы к каноническому виду заключается в последовательном выделении полных квадратов.
Пример 3. Привести к каноническому виду квадратичную форму 
Итак, невырожденное линейное преобразование 
приводит данную квадратичную форму к каноническому виду
Канонический вид квадратичной формы не является однозначным, так как одна и та же квадратичная форма может быть приведена к каноническому виду многими способами. Однако полученные разными способами квадратичные формы имеют ряд общих свойств.
Сформулируем одно из этих свойств, которое выражает закон инерции квадратичных форм, и заключается в следующем: все канонические формы, к которым приводится данная квадратичная форма, имеют:
1) одно и то же число нулевых коэффициентов;
2) одно и то же число положительных коэффициентов;
3) одно и то же число отрицательных коэффициентов.
Определение 1. Квадратичная форма L (x1, x2, . xn) называется положительно определенной, если для всех действительных значений x1, x2, . xn используется неравенство L (x1, x2, . xn) > 0.
Определение 2. Если L (x1, x2, . xn) является положительно определенной формой, то квадратичная формаL (x1, x2, . xn) T AX была положительно (отрицательно) определенной, необходимо и достаточно, чтобы все собственные значения λi (i = 1, 2, . n) матрицы A были положительными (отрицательными).
Данную теорему приводим без доказательства.
Во многих случаях для установления знакоопределенности квадратичной формы удобно применять критерии Сильвестра.
ТЕОРЕМА 3. Для того чтобы квадратичная форма была положительно определенной, необходимо и достаточно, чтобы все главные миноры матрицы этой формы были положительными, то есть


Следует заметить, что для отрицательно определенных квадратичных форм знаки главных миноров чередуются, начиная со знака «минус» для минора первого порядка.
Например, квадратичная форма L в примере 2 является положительно определенной на основании теоремы 2, так как корни характеристического уравнения λ1 = 6 и λ2 = 1 являются положительными.
Второй способ. Так как главные миноры матрицы A

Видео:Лекция 8. Решение матричных уравненийСкачать

Квадратичные формы
Однородный многочлен второй степени относительно переменных
называется квадратичной формой от этих переменных. Если взять 
Выражение (1.28), а следует и квадратичная форма (1.26) полностью определяется матрицей 
Выполняя замену базиса, квадратичную форму (1.26) можно привести к виду:
где 


Выражение (1.29) называется каноническим видом квадратичной формы (1.26).
Рассмотрим квадратичную форму 

Тогда квадратичную форму можно записать так:
Квадратичная форма 



Если 

Решение примеров:
Пример 1.99
является отрицательно определенной.
Пример 1.100
Используя теорию квадратичных форм, привести к каноническому виду уравнения линии второго порядка
Решение. Уравнение линии запишем в виде 
Сложим характеристическое уравнение матрицы 

Корни уравнения 


Свойства квадратичной формы (1.30) связаны с собственными числами матрицы
Пример 1.101
Привести к каноническому виду уравнения линии
Решение. Группа старших членов этого уравнения квадратическую форму 
Собственными значениями будут числа 





Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
Видео:Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

Квадратные СЛАУ. Матричный метод решения
С помощью данного метода можно находить решение только для квадратных СЛАУ.
Видео:Система линейных уравнений. Метод обратной матрицы. Матричный метод.Скачать

Матричный метод решения
Запишем заданную систему в матричном виде:
Если матрица $$A$$ невырождена, то тогда с помощью операций над матрицами выразим неизвестную матрицу $$X$$ . Операция деления на множестве матриц заменена умножением на обратную матрицу, поэтому домножим последнее равенство на матрицу $A^$ слева:
$$A^ A X=A^ B Rightarrow E X=A^ B Rightarrow$$ $$X=A^ B$$
Поэтому, чтобы найти неизвестную матрицу $$X$$ надо найти обратную матрицу к матрице системы и умножить ее справа на вектор-столбец свободных коэффициентов.
Данный метод удобно применять тогда, когда нужно решить много одинаковых систем с разными правыми частями.
Видео:§28 Матричные уравненияСкачать

Примеры решения систем уравнений
Задание. Найти решение СЛАУ $left<begin 5 x_+2 x_=7 \ 2 x_+x_=9 endright.$ матричным методом.
$$X=left(begin x_ \ x_ endright)=A^ B=left(begin 1 & -2 \ -2 & 5 endright) cdotleft(begin 7 \ 9 endright)=$$ $$=left(begin -11 \ 31 endright) Rightarrowleft(begin x_ \ x_ endright)=left(begin -11 \ 31 endright)$$
Две матрицы одного размера равны, если равны их соответствующие элементы, то есть в итоге имеем, что $x_=-11, x_=31$
Ответ. $x_=-11, x_=31$
Задание. Решить с помощью обратной матрицы систему $left<begin 2 x_+x_+x_=2 \ x_-x_=-2 \ 3 x_-x_+2 x_=2 endright.$
Решение. Запишем данную систему в матричной форме:
где $A=left(begin 2 & 1 & 1 \ 1 & -1 & 0 \ 3 & -1 & 2 endright)$ — матрица системы, $X=left(beginx_ \ x_ \ x_endright)$ — столбец неизвестных, $X=left(begin x_ \ x_ \ x_ endright)$ — столбец правых частей. Тогда $X=A^ B$
Найдем обратную матрицу $X=A^$ к матрице $A$ с помощью союзной матрицы:
Здесь $Delta=|A|$ — lt a href=»formules_6_11.php» title=»Методы вычисления определителей матрицы: теоремы и примеры нахождения»>определитель матрицы $A$ ; матрица $tilde$ — союзная матрица, она получена из исходной матрицы $A$ заменой ее элементов их алгебраическими дополнениями. Найдем $A$ , для этого вычислим алгебраические дополнения к элементам матрицы $A$ :
Определитель матрицы $A$
$$Delta=left|begin 2 & 1 & 1 \ 1 & -1 & 0 \ 3 & -1 & 2 endright|=2 cdot(-1) cdot 2+1 cdot(-1) cdot 1+1 cdot 0 cdot 3-$$ $$-3 cdot(-1) cdot 1-(-1) cdot 0 cdot 2-1 cdot 1 cdot 2=-4 neq 0$$
🎥 Видео
Математика без Ху!ни. Метод Гаусса.Скачать

Квадратные уравнения от «А» до «Я». Классификация, решение и теорема Виета | МатематикаСкачать

Решение системы уравнений методом обратной матрицы.Скачать

Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Квадратное уравнение. Практическая часть. 1ч. 8 класс.Скачать

Привести квадратичную форму к каноническому видуСкачать
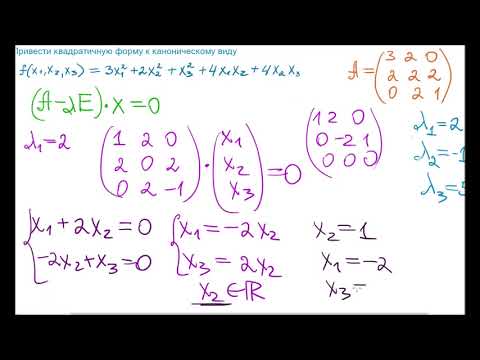
Квадратное уравнение. 8 класс.Скачать

Неполные квадратные уравнения. Алгебра, 8 классСкачать

Решение системы уравнений методом ГауссаСкачать

Матричные уравнения Полный разбор трех типов матричных уравненийСкачать

Комплексные корни квадратного уравненияСкачать

Быстрый способ решения квадратного уравненияСкачать

Квадратное уравнение. Практическая часть. 2ч. 8 класс.Скачать






























