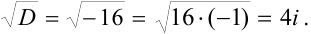Квадратное уравнение с отрицательным дискриминантом через комплексные числа (2 видео)

Содержание

Квадратное уравнение с отрицательным дискриминантом через комплексные числа
Решение квадратных уравнений с отрицательным дискриминантом
Пример №42.4.
Числа. Извлечение корней из комплексных чисел. Квадратное уравнение с комплексными корнями.
Как извлечь корень из произвольного комплексного числа?
💥 Видео

Видео:Комплексные корни квадратного уравненияСкачать

Квадратное уравнение с отрицательным дискриминантом через комплексные числа

КОМПЛЕКСНЫЕ ЧИСЛА XI

§ 253. Извлечение корней квадратных из отрицательных чисел.
Решение квадратных уравнений с отрицательными дискриминантами

Таким образом, существуют по крайней мере два значения корня квадратного из — 1, а именно i и — i . Но, может быть, есть еще какие-нибудь комплексные числа, квадраты которых равны — 1?

Чтобы выяснить этот вопрос, предположим, что квадрат комплексного числа а + bi равен — 1. Тогда

Два комплексных числа равны тогда и только тогда, когда равны их действительные части и коэффициенты при мнимых частях. Поэтому

Согласно второму уравнению системы (1) хотя бы одно из чисел а и b должно равняться нулю. Если b = 0, то из первого уравнения получается а 2 = — 1. Число а действительное, и поэтому а 2 > 0. Неотрицательное число а 2 не может равняться отрицательному числу — 1. Поэтому равенство b = 0 в данном случае невозможно. Остается признать, что а = 0, но тогда из первого уравнения системы получаем: — b 2 = — 1, b = ± 1.

Следовательно, комплексными числами, квадраты которых равны —1, являются только числа i и —i, Условно это записывается в виде:

Аналогичными рассуждениями учащиеся могут убедиться в том, что существует ровно два числа, квадраты которых равны отрицательному числу —а. Такими числами являются √ a i и —√ a i . Условно это записывается так:

Под √ a здесь подразумевается арифметический, то есть положительный, корень. Например, √ 4 = 2, √ 9 =.3; поэтому

Если раньше при рассмотрении квадратных уравнений с отрицательными дискриминантами мы говорили, что такие уравнения не имеют корней, то теперь так говорить уже нельзя. Квадратные уравнения с отрицательными дискриминантами имеют комплексные корни. Эти корни получаются по известным нам формулам. Пусть, например, дано уравнение x 2 + 2х + 5 = 0; тогда

Итак, данное уравнение имеет два корня: х₁ = — 1 +2i, х₂ = — 1 — 2i. Эти корни являются взаимно сопряженными. Интересно отметить, что сумма их равна — 2, а произведение 5, так что выполняется теорема Виета.

2022. (У с т н о.) Решить уравнения:

2023. Найти все комплексные числа, квадраты которых равны:

2024. Решить квадратные уравнения:

Решить системы уравнений (№ 2025, 2026):

2027. Доказать, что корни квадратного уравнения с действительными коэффициентами и отрицательным дискриминантом являются взаимно сопряженными.

2028. Доказать, что теорема Виета верна для любых квадратных уравнений, а не только для уравнений с неотрицательным дискриминантом.

2029. Составить квадратное уравнение с действительными коэффициентами, корнями которого являются:

2030. Составить квадратное уравнение с действительными коэффициентами, один из корней которого равен (3 — i) (2i — 4).

2031. Составить квадратное уравнение с действительными коэффициентами, один из корней которого равен 32 — i
1— 3i .

Видео:Отрицательный дискриминантСкачать

Решение квадратных уравнений с отрицательным дискриминантом

Рассмотрим решение квадратных уравнений, дискриминант которых отрицателен:

Пример №42.4.

Решить уравнение: .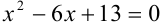

Решение:

Найдем дискриминант: .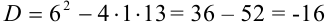

Тогда .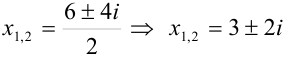

Ответ: .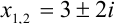

Видим, что если дискриминант квадратного уравнения отрицателен, то уравнение имеет решения на множестве комплексных чисел. В ответе получаются два сопряженных комплексных числа. Это очень важный результат: теперь мы знаем, что абсолютно любое квадратное уравнение имеет два корня на множестве комплексных чисел.

Подобное утверждение, известное под названием «основная теорема алгебры», было доказано Гауссом в конце XVIII века: любое алгебраическое уравнение -й степени имеет комплексных корней (при этом некоторые корни являются кратными). Эти результаты подчеркивают ту исключительную роль, которую играют комплексные числа в теории алгебраических уравнений.

Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:

Другие лекции по высшей математике, возможно вам пригодятся:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

Видео:Как найти корни квадратного уравнения с отрицательным дискриминантом? Теория комплексных чисел.Скачать

Числа. Извлечение корней из комплексных чисел. Квадратное уравнение с комплексными корнями.

Рассматривать будем на таком примере:

Если говорить о действительных числах, то, вы знаете, что корень из отрицательного числа нельзя извлекать. Однако в комплексных числах можно. Если конкретнее, 2 корня:

Выполним проверку того, что эти корни и права оказываются решением уравнения:

Что и требовалось доказать.

Зачастую используют сокращенную запись, корни записывают в одну строчку в таком виде: .

Такие корни являются сопряженными комплексными корнями.

Теперь вы знаете как можно извлечь квадратный корень из отрицательного числа. Приведем еще несколько примеров:

, ,

В каждом случае получаем 2 сопряженных комплексных корня.

Решим квадратное уравнение .

Первым шагом определим дискриминант уравнения:

В нашем случае дискриминант оказался отрицательным, и в случае с действительными числами у уравнения нет решений, но у нас вариант с комплексными числами, поэтому можем продолжать решение:

Как известно из формул дискриминанта у нас образуется 2 корня:

– сопряженные комплексные корни

Т.о., у уравнения есть 2 сопряженных комплексных корня:

Теперь можно решить любое квадратное уравнение!

У любого уравнения с многочленом n-ой степени есть ровно n корней, некоторые из них могут быть комплексными.

Видео:Комплексные корни квадратных уравнений. 11 класс.Скачать

Как извлечь корень из произвольного комплексного числа?

Рассмотрим уравнение z n = w, либо, записав в другом виде: . Здесь n может принимать всякое натуральное значение, которое больше 1-цы.

В частности, при n = 2 получаем квадратный корень .

У уравнения типа есть ровно n корней z₀, z₁, z₂, … z_n_-1, которые можно вычислить с помощью формулы:

где – это модуль комплексного числа w,

φ – его аргумент,

а параметр k принимает значения: .

Найдем корни уравнения: .

Перепишем уравнение как: .

В этом примере , , поэтому у уравнения будет 2 корня: z₀ и z₁. Детализируем общую формулу:

, .

Далее найдем модуль и аргумент комплексного числа :

Число w находится в 1-ой четверти, значит:

Помним, что определяя тригонометрическую форму комплексного числа лучше делать чертеж.

Детализируем еще немного общую формулу:

, .

Так подобно расписывать не обязательно. Здесь мы это сделали, что бы было ясно откуда что образовалось.

Подставляем в формулу значение k = 0 и получаем 1-й корень:

Подставляем в формулу значение k = 1 и получаем 2-й корень:

Ответ: ,

Если необходимо, корни, которые мы получили можно перевести обратно в алгебраическую форму.

Часто вычисленные корни нужно изобразить геометрически:

Как выполнить чертеж?

Для начала на калькуляторе вычисляем, чему равен модуль корней и чертим с помощью циркуля окружность этого радиуса. Все корни будем откладывать на данной окружности.