Квадратное уравнение с дробью график

В этой статье мы поговорим о том, что такое квадратичная функция, научимся строить ее график и определять вид графика в зависимости от знака дискриминанта и знака старшего коэффициента.
Итак.

Функция вида , где 0″ title=»a0″/> называется квадратичной функцией.

В уравнении квадратичной функции:

a — старший коэффициент

b — второй коэффициент

с — свободный член.

Графиком квадратичной функции является квадратичная парабола, которая для функции имеет вид:

Обратите внимание на точки, обозначенные зелеными кружками — это, так называемые «базовые точки». Чтобы найти координаты этих точек для функции , составим таблицу:

Внимание! Если в уравнении квадратичной функции старший коэффициент , то график квадратичной функции имеет ровно такую же форму, как график функции при любых значениях остальных коэффициентов.

График функции имеет вид:

Для нахождения координат базовых точек составим таблицу:

Обратите внимание, что график функции симметричен графику функции относительно оси ОХ.

Итак, мы заметили:

Если старший коэффициент a>0 , то ветви параболы напрaвлены вверх .

Если старший коэффициент a , то ветви параболы напрaвлены вниз .

Второй параметр для построения графика функции — значения х, в которых функция равна нулю, или нули функции. На графике нули функции — это точки пересечения графика функции с осью ОХ.

Поскольку ордината (у) любой точки, лежащей на оси ОХ равна нулю, чтобы найти координаты точек пересечения графика функции с осью ОХ, нужно решить уравнение .

В случае квадратичной функции нужно решить квадратное уравнение .

В процессе решения квадратного уравнения мы находим дискриминант: , который определяет число корней квадратного уравнения.

И здесь возможны три случая:

1. Если ,то уравнение не имеет решений, и, следовательно, квадратичная парабола не имеет точек пересечения с осью ОХ. Если 0″ title=»a>0″/>,то график функции выглядит как-то так:

2. Если ,то уравнение имеет одно решение, и, следовательно, квадратичная парабола имеет одну точку пересечения с осью ОХ. Если 0″ title=»a>0″/>,то график функции выглядит примерно так:

3 . Если 0″ title=»D>0″/>,то уравнение имеет два решения, и, следовательно, квадратичная парабола имеет две точки пересечения с осью ОХ:

,

Если 0″ title=»a>0″/>,то график функции выглядит примерно так:

Следовательно, зная направление ветвей параболы и знак дискриминанта, мы уже можем в общих чертах определить, как выглядит график нашей функции.

Следующий важный параметр графика квадратичной функции — координаты вершины параболы:

Прямая, проходящая через вершину параболы параллельно оси OY является осью симметрии параболы.

И еще один параметр, полезный при построении графика функции — точка пересечения параболы с осью OY.

Поскольку абсцисса любой точки, лежащей на оси OY равна нулю, чтобы найти точку пересечения параболы с осью OY, нужно в уравнение параболы вместо х подставить ноль: .

То есть точка пересечения параболы с осью OY имеет координаты (0;c).

Итак, основные параметры графика квадратичной функции показаны на рисунке:

Рассмотрим несколько способов построения квадратичной параболы. В зависимости от того, каким образом задана квадратичная функция, можно выбрать наиболее удобный.

1. Функция задана формулой .

Рассмотрим общий алгоритм построения графика квадратичной параболы на примере построения графика функции

1. Направление ветвей параболы.

Так как 0″ title=»a=2>0″/>,ветви параболы направлены вверх.

2. Найдем дискриминант квадратного трехчлена

0″ title=»D=b^2-4ac=9-4*2*(-5)=49>0″/>

Дискриминант квадратного трехчлена больше нуля, поэтому парабола имеет две точки пересечения с осью ОХ.

Для того, чтобы найти их координаты, решим уравнение:

,

3. Координаты вершины параболы:

4. Точка пересечения параболы с осью OY: (0;-5),и ей симметричная относительно оси симметрии параболы.

Нанесем эти точки на координатную плоскость, и соединим их плавной кривой:

Этот способ можно несколько упростить.

1. Найдем координаты вершины параболы.

2. Найдем координаты точек, стоящих справа и слева от вершины.

Воспользуемся результатами построения графика функции

Кррдинаты вершины параболы

Ближайшие к вершине точки, расположенные слева от вершины имеют абсциссы соответственно -1;-2;-3

Ближайшие к вершине точки, расположенные справа имеют абсциссы соответственно 0;1;2

Подставим значения х в уравнение функции, найдем ординаты этих точек и занесем их в таблицу:

Нанесем эти точки на координатную плоскость и соединим плавной линией:

2 . Уравнение квадратичной функции имеет вид — в этом уравнении — координаты вершины параболы

или в уравнении квадратичной функции , и второй коэффициент — четное число.

Построим для примера график функции .

Вспомним линейные преобразования графиков функций. Чтобы построить график функции , нужно

• сначала построить график функции ,
• затем одинаты всех точек графика умножить на 2,
• затем сдвинуть его вдоль оси ОХ на 1 единицу вправо,
• а затем вдоль оси OY на 4 единицы вверх:

Теперь рассмотрим построение графика функции . В уравнении этой функции , и второй коэффициент — четное число.

Выделим в уравнении функции полный квадрат:

Следовательно, координаты вершины параболы: . Старший коэффициент равен 1, поэтому построим по шаблону параболу с вершиной в точке (-2;1):

3 . Уравнение квадратичной функции имеет вид y=(x+a)(x+b)

Построим для примера график функции y=(x-2)(x+1)

1. Вид уравнения функции позволяет легко найти нули функции — точки пересечения графика функции с осью ОХ:

(х-2)(х+1)=0, отсюда

2. Координаты вершины параболы:

3. Точка пересечения с осью OY: с=ab=(-2)(1)=-2 и ей симметричная.

Нанесем эти точки на координатную плоскость и построим график:

График квадратичной функции.

Перед вами график квадратичной функции вида .

Кликните по чертежу.
Подвигайте движки.
Исследуйте зависимость
— ширины графика функции от значения коэффициента ,
— сдвига графика функции вдоль оси от значения ,

— сдвига графика функции вдоль оси от значения
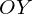
— направления ветвей параболы от знака коэффициента
— координат вершины параболы от значений и :

И.В. Фельдман, репетитор по математике.

Видео:ЭЛЕМЕНТАРНО, ВАТСОН! Квадратичная Функция и ее график ПараболаСкачать

Элективное занятие «Дробно-квадратичные функции. Классификация графиков»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Выберите документ из архива для просмотра:

Выбранный для просмотра документ #U0414#U041a#U0424.pptx

Описание презентации по отдельным слайдам:

Дробно-квадратичные функции. Классификация графиков.

Цель : Исследовать свойства и графики некоторых дробно-квадратичных функций.

Задачи : Обобщить свойства дробно-квадратичных функций. Провести классификацию их графиков. Найти методы построения графиков дробно-квадратичных функций.

Определение. Дробно-квадратичной называется функция вида y = ax² + bx + c , где a, b, c, p, q, r – px² + qx + r таковы, что в числителе дроби – многочлен 2, 1 или 0 степени, отличный от нуля, а в знаменателе – многочлен 1 или 2 степени. При этом a ≠ 0 и p ≠ 0 одновременно. Также многочлены не пропорциональны и не имеют общих корней, т.е. дробь несократима.

Тогда все такие функции можно разделить на две группы: 1 группа 2 группа y = ax² + bx + c , px² + qx + r p ≠0 y = ax² + bx + c , qx + r q ≠ 0

В свою очередь, все ДКФ первой группы можно разделить на три подгруппы, ставя в основу деления условия: D > 0; D = 0; D 0 » onclick=»aa_changeSlideByIndex(33, 0, true)» >

1 группа D = q² — 4pr, D > 0

1.D(y)=R,кромеx=tиx=s 2.E(y) =(-∞;n][m; +∞) 3.Экстремумадва:у=n,у=m(в точкахВиС) 4.Пять промежутков монотонности 5.Асимптотыx=t,x=s,y= 6.Точка пересечения с асимптотами — точкаА 7.Симметриинет. 1.D(y)=R,кромеx=tиx=s 2.E(y) =(-∞;m](α;+∞) или (-∞;α)[m; +∞) 3.Экстремум один:у=m(точкаВ) 4.Четыре промежутка монотонности. 5.Асимптотыx=t;x = s 6.Точек пересечения с асимптотами нет 7. Ось симметрииx =-b, x =s + t. 2a 2

1.D(y)=R,кромеx=tиx=s E(y) =R 3.Экстремумовнет 4.Три промежутка монотонности. 5.Асимптотыx=t;x=s.y= 6.Точек пересечения с асимптотами нет. 7.Симметрии нет.

2 группа D = q² — 4pr, D = 0

1.D(y)=Rкромеx=t 2.E(y) =(-∞;m]или [m; +∞) 3.Экстремумодин:у=m(точкаВ) 4.Три промежутка монотонности. 5.Асимптотыx=t;y= 6.Точекпересечения с асимптотами нет. 7.Симметрии нет. 1.D(y) =Rкромеx=t 2.E(y) =(-∞;α)или (α; +∞) 3.Экстремумов нет. 4.Два промежутка монотонности. 5.Асимптотыx=t;y= 6.Точек пересечения с асимптотаминет Осьсимметрииx =- b. 2a

3 группа D = q² — 4pr, D

Выбранный для просмотра документ #U041f#U0440#U043e#U0435#U043a#U0442. #U0414#U0440#U043e#U0431#U043d#U043e-#U043a#U0432. #U0444#U0443#U043d#U043a#U0446#U0438#U0438.docx

Тема проекта: Дробно-квадратичные функции. Классификация графиков.

Объект исследования: Изучение свойств дробно-квадратичных функций.

Цель проекта: Исследовать свойства некоторых дробно-квадратичных функций.

Обобщить свойства дробно-квадратичных функций.

Провести классификацию их графиков.

Найти методы построения графиков дробно-квадратичных функций.

Экспериментальная часть (выбор функций, их исследование и построение графиков).

Обобщение полученной информации, выдвижение гипотез.

Попытка доказательства выявленных свойств в общем виде.

Заполнение сводной классификационной таблицы.

Результат проекта: таблица разновидностей графиков квадратичных функций.

Построение графиков функций — одна из интереснейших тем в школьной математике. Один из крупнейших математиков нашего времени Израиль Моисеевич Гельфанд писал: «Процесс построения графиков является способом превращения формул и описаний в геометрические образы. Это – построение графиков – является средством увидеть формулы и функции и проследить, каким образом эти функции меняются. Например, если написано y = x 2 , то мы сразу видим параболу; если y = x 2 – 4 , мы видим параболу, опущенную на четыре единицы; если же y = 4 — x 2 , то мы видим предыдущую параболу, перевернутую вниз. Такое умение видеть сразу и формулу, и ее геометрическую интерпретацию – является важным не только для изучения математики, но и для других предметов. Это умение, которое остается с нами на всю жизнь, подобно умению ездить на велосипеде, печатать на машинке или водить машину».

На уроках математики мы строим в основном простейшие графики – графики элементарных функций. Только в 11 классе будем строить графики более сложных функций с помощью производной.

Однако графики некоторых сложных функций можно строить без использования производной, т.е. элементарными способами. Именно разложение сложной функции на элементарные и, в дальнейшем, построение графиков таких функций, и заинтересовало нас при более детальном рассмотрении дробно-квадратичных функций .

Дробно-квадратичные функции – это функции, которые в школьных учебниках и популярной литературе встречаются довольно часто. Однако изучение их ограничивается какими-то конкретными функциями. Между тем, классификация графиков таких функций во многом бы облегчила работу учителей и учащихся.

Определение дробно-квадратичной функции.

Дробно-квадратичной называется функция вида

y = ax² + bx + c , где a, b, c, p, q, r –

px ² + qx + r таковы, что

в числителе дроби – многочлен 2, 1 или 0 степени, отличный от нуля, а в знаменателе – многочлен 1 или 2 степени. При этом a ≠ 0 и p ≠ 0 одновременно. Также многочлены не пропорциональны и не имеют общих корней, т.е. дробь несократима.

Тогда условно можно разделить все такие функции на две группы :

1группа:

2группа:

, q ≠ 0.

Общность свойств дробно-квадратичной функции диктуется , в первую очередь, наличием или отсутствием корней в знаменателе дроби, т.е. знаком числа D = b ² — 4 ac . С этим числом связана структура области определения дробно-квадратичных функций.

Поэтому все дробно-квадратичные функции первой группы можно разделить на три подгруппы,
ставя в основу деления условия:

Построение графиков некоторых дробно-квадратичных функций.

Пример 1 . Построить график функции

. ( D > 0).

Выделив целую часть, будем иметь

.

Дробь изобразим в виде суммы элементарных дробей:

.

Построим графики функций:

После сложения этих графиков получаем график заданной функции:

(рис. 2)

На основании построенного графика проводим исследование данной функции:

Три промежутка монотонности.

Асимптоты: х = — 1 , x = 3, y = 1 .

Точек пересечения с асимптотами нет.

Пример 2. Построим график функции : y = ( D = 0).

Преобразуем данную дробь:

= 1 — = 1 – = 1 — —

Построим график каждой из функций у = 1, у = — и у = — .

В результате сложения графиков получаем график функции у =

Свойства данной функции:

Д(у) = R , кроме x = 2.

Два промежутка монотонности.

Асимптоты: x = 2 , y = 2 .

Точек пересечения с асимптотами нет.

Пример 3. Построим график функции у = ( D 0).

Преобразуем данную функцию в сумму и произведение элементарных функций:

У = = = 1 + = 1 + ( x – 2) ∙ .

Построим график каждой из функций

у = 1, у = х – 2, у = , у =

у = ( x – 2) ∙ .

Видео:Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

Квадратичная функция. Построение параболы

О чем эта статья:

8 класс, 9 класс, ЕГЭ/ОГЭ

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Видео:Как построить график функции без таблицыСкачать

Основные понятия

Функция — это зависимость «y» от «x», при которой «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции.

Задать функцию означает определить правило в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:

• Табличный способ. Помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
• Графический способ: наглядно.

• Аналитический способ, через формулы. Компактно и можно посчитать функцию при произвольном значении аргумента из области определения.
• Словесный способ.

График функции — это объединение всех точек, когда вместо «x» можно подставить в функцию произвольные значения и найти координаты этих точек.

Еще быстрее разобраться в теме и научиться строить график квадратичной функции можно на курсах по математике в онлайн-школе Skysmart.

Видео:Решение квадратных неравенств графическим методом. 8 класс.Скачать

Построение квадратичной функции

Квадратичная функция задается формулой y = ax 2 + bx + c, где x и y — переменные, a, b, c — заданные числа, обязательное условие — a ≠ 0. В уравнении существует следующее распределение:

График квадратичной функции — парабола, которая имеет следующий вид для y = x 2 :

Точки, обозначенные зелеными кружками называют базовыми точками. Чтобы найти их координаты для функции y = x 2 , нужно составить таблицу:

x

y

Если в уравнении квадратичной функции старший коэффициент равен единице, то график имеет ту же форму, как y = x 2 при любых значениях остальных коэффициентов.

График функции y = –x 2 выглядит, как перевернутая парабола:

Зафиксируем координаты базовых точек в таблице:

x

y

Посмотрев на оба графика можно заметить их симметричность относительно оси ОХ. Отметим важные выводы:

• Если старший коэффициент больше нуля a > 0, то ветви параболы напрaвлены вверх.
• Если старший коэффициент меньше нуля a 2 + bx + c, для построения которой нужно решить квадратное уравнение ax 2 + bx + c = 0. В процессе найдем дискриминант D = b 2 — 4ac, который даст нам информацию о количестве корней квадратного уравнения.

Рассмотрим три случая:

1. Если D 0,то график выглядит так:

1. Если D = 0, то уравнение имеет одно решение, а парабола пересекает ось ОХ в одной точке. Если a > 0, то график имеет такой вид:
2. Если D > 0, то уравнение имеет два решения, а парабола пересекает ось ОХ в двух точках, которые можно найти следующим образом:

Если a > 0, то график выглядит как-то так:

0″ height=»671″ src=»https://lh6.googleusercontent.com/8ryBuyxmK9S2EbnsNc4AE5PEl_NpIg0RAM_Y_V8wUP-zREEHNgi9QoQTl8FXxoujjWRAvf3s-MPRsXsoepaLLSTHDX-ReGtrsnLQp4dW3WaEyPF2ywjVpYFXlDIpAEHoIiwlxiB7″ width=»602″>

На основе вышеизложенного ясно, что зная направление ветвей параболы и знак дискриминанта, у нас есть понимание, как будет выглядеть график конкретной функции.

Координаты вершины параболы также являются важным параметром графика квадратичной функции и находятся следующим способом:

Ось симметрии параболы — прямая, которая проходит через вершину параболы параллельно оси OY.

Чтобы построить график, нам нужна точка пересечения параболы с осью OY. Так как абсцисса каждой точки оси OY равна нулю, чтобы найти точку пересечения параболы y = ax 2 + bx + c с осью OY, нужно в уравнение вместо х подставить ноль: y(0) = c. То есть координаты этой точки будут соответствовать: (0; c).

На изображении отмечены основные параметры графика квадратичной функции:

Видео:Неполные квадратные уравнения. Алгебра, 8 классСкачать

Алгоритм построения параболы

Рассмотрим несколько способов построения квадратичной параболы. Наиболее удобный способ можно выбрать в соответствии с тем, как задана квадратичная функция.

Видео:7 класс, 35 урок, Графическое решение уравненийСкачать

Уравнение квадратичной функции имеет вид y = ax 2 + bx + c.

Разберем общий алгоритм на примере y = 2x 2 + 3x — 5.

Как строим:

1. Определим направление ветвей параболы. Так как а = 2 > 0, ветви параболы направлены вверх.
2. Найдем дискриминант квадратного трехчлена 2x 2 + 3x — 5.

D = b 2 — 4ac = 9 — 4 * 2 * (-5) = 49 > 0

В данном случае дискриминант больше нуля, поэтому парабола имеет две точки пересечения с осью ОХ. Чтобы найти их координаты, решим уравнение:

2x 2 + 3x — 5 = 0 2 + 3x — 5 = 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAPoAAAAyCAYAAAB1V8bkAAAJyElEQVR4Ae2c16sUwRLGfdRX/wXFB30QFFQUQUyIKCIGBEEQzCCoKIgB01ExZwVz4JpzztljwJxzzjlnrcuvL33unD2zOzO7OzvuThU0u5N6uuvrr7u6unrKiYpqQDVQ8BooV/A11AqqBlQDokTXRqAaiIEGlOgxAFmrqBpQomsbUA3EQANK9BiArFVUDSjRtQ2oBmKgASV6DEDWKqoGlOjaBlQDMdBAQRH9z58/8vv3b5P+/v2bMXy/fv0S8kxMGWesGRgNpIMXz7jhkg28CxmWgiH69+/f5dSpU7JixQpZtmyZXLx4UX7+/JkUOxoGjSaVTJw4UVatWiUbNmwoSYcPH071iF7zqYGgeNlsT58+LZMnTy7BA2y2bNkib9++tbfor4sGCobogD19+nR5/fq1nDx5Upo0aSLHjh2TZD39x48f5ebNmy4q+d8pRo327dtLo0aNTF6NGzeWevXqCeRXyVwDQfHijXTMmzZtMjiAL6lu3brSuXNnuXfvXuaFKuAcCobojOQDBgwwgD948EAg5ubNm42Z54bfjRs3ZMqUKW6XzDk6jP379wsjD/LmzRtZt26dvHr1KukzesG/BoLiRc5gceXKFZM4/vbtmxw6dEguXbokP3788P/yGN5ZMET/8uWLvHv3Tt6/f2/Muh49esj169eTQupF9MQHIfm1a9cST+txmhoIipfba86fPy9Hjx4VrDOV1BooGKJTTYh++fJlGTt2rCxevNgcJ6t+EKIz3587d26yrPR8mhoIglfiK549e2Y6dHBU8dZA3hH9+PHjYhNmnFO+fv1qTOwDBw5Ily5dhF+nQ47ndu/ebdLChQule/fuJcecp9E477d5d+zYUW7fvm0P9TeABixW/AbBCz+LffbChQtl3rh69WpZsmSJjuZlNON+Iu+IDkGZW+N427Ztm6nVp0+f5MiRI6Zh2Dl1hw4dZOjQoaVGdebc1oM+a9Ys48Sxx/y6zfUePnwoVapUcdeenvXUQLp4LV261OA8bdo0g5nzRR8+fJBhw4YJeav400DeEf3Ro0dmZGD+/fLlS1NLzLjhw4fLmDFjhEaA4DHv16+fGeHdVOHXdKczqVy5slsWes6HBtLF6/HjxwZn/CLPnz8v9aZbt25Jt27dlOiltJL6IO+I7lYdTPY1a9bIjBkz5M6dO7Jjxw5hRN++fXtSb6xfos+ZM0cqVark9trQzrEmXFxc7LnOH1oBQs44HbycRTpz5oy0a9funyA6DkGW/NavX19mauIsc+J/OkCmJliRL168ME7FVM7jxOeDHhcE0ak05KD3P3v2rFkWO3HihHz+/DmpPlh3XbRoUdLr9gL5LF++3B6G+nv//n3ZuHGjDBw4UDp16pS0kwq1EDnKPChezmI9efJEtm7dmnJVxXl/WP8PHjxopoxXr141RG3Tpo0JsPLzPqaaLVq0kDp16kjDhg2lb9++JgbEz7Pp3FMwRKfyBLkwX2fpxivqjbm8Nf1TKY77WK/NhVBuGvGoUaNMHID1N+Ti3VG8IwhezvIR5gwm/EYlrBgMGTJE9u3bZxy4YDV69Gjf/py9e/fKypUrjSVKLEDYqwcFRfSoQM/2e2fOnGmivgqd6NnWWy7zI3CqefPmUlRUVOIXgrzly5cXfEZewr2Y/XTuyaI3vfIIcj1tolM4lpyIBZ83b56MGzdO9uzZY0YjwkSfPn0apBx6r0MDYRBd8XIoOAt/sRiZU0N4az2OHz9eKlSo4MvSgOgs6RKIBYdIYUraRMfsYpkL84m5cc+ePY1DYv78+dKnTx/B2eAlmKldu3b1TISy5luII8s/XnWbNGmSMC9PlDCIrniJcXB6YcJ15s9+JHEkrlq1qixYsMDPowLRcRqzSgSHiOkI0xeUNtHpxXBUIQQ3tGrVKnLniC8N58FNYRBd8QoOPES2Php8Agw2dvR25gZRcaaNHDnSeTrlf/JxdhTsuMQacJ5LmUHAi2kT3b6HyrNBoXXr1uYUBXVThr3f+YuCcGp4JZRsFYAV8K8lt1hremqveuE4RAeJEgbR7Tvigpfb1JG6e2HCde5DCJbCM16rVi2T2D9BiLVT6Agwv3GsgSXPumHqfAZ+sLqCNWfbNQ455ve8MwxJm+gsXeF0YFcXPRlRaAiebD/OCO5l/XDQoEGeCTPHhqZWq1ZN/rVElF2iTJ061bNemHkEhiRKGESPG141atRIVKtZevXT3tjz7kcYgIioZDRmtyM6Zk09sf0zbYIndkBgabFt27ZmeZeYAgQzvmLFimWe9VMOP/ekTXTWMXv37m16uF69esmECRNMZdgDzgcgVIJrwLm8Vr9+fSECjM4wG6J4ZUOL/8+DgQdSwwGccIRkk4jITBRGaZZM8V/ZlRRGdIJlwJzBsX///gKPwpK0iY7HkArSgKgwu8XYMnju3LmkgSr0ZNZUCatCfvLFtKIHtj2sn2dycY8NmCGcF6cQIwXx+dmQfMMLfEj/qjA1Yx29ZcuWpRLmfaLcvXtXBg8eLCNGjChxUoM1mBAdt3btWmP9ZatTT3w/x2kTHcKytAB5EeYmyYiDecpWz9mzZyf9EIRb4cI6Rw/KikGcLI98w4vlWkKYC0Uw5xkEMeGt4A/Akc28P+wBMG2i28L6+WV7IruRmjVrVmK6+HkujHuYL+3atcuUhbm/SlkNRI0Xn/iqWbOmaTNlS5d/ZzDzITOhslFJTohO5Rg98WDaOUoUFabXpBExV2JThBI9OQpR4YX1x3SQb/UxOBSCYO2yA48RPCqJFdGZmxN8w/q/Ej11k4uK6ERXMqflw4+FQvTUms7N1VgRnYgndq2RlOipG1gURCf2myhLpldNmzZVoqeGKNDV2BAdj+bOnTuNcpTo3m0k10THrCVohCAiRInujVGQO2JDdJYA8bQTpIJHt3bt2mZtk1FEpawGck10PrRB4BEf4QQjgqIIK2UbqErmGsgJ0fE2AmL16tWFj/oRwpprYcRgVCcR+URsPkELBCyolNZAFHgRVcZyrcWoQYMGwtd97KfBSpdQj4JqICdEZ3kBkwwQIZZXLHDQSvi9H687G/wJgyREkl+7McdvHnG4L0q8WG9mUOCDnASf4DxVyVwDOSF65sXMXg6QnYbMMh+/fjfgZK8EmlMqDYAPzji7WyyqQSFVGfPxWuyIno8gaZlVA5lqQImeqQb1edVAHmhAiZ4HIGkRVQOZakCJnqkGI3m+WIrKlZOi45G8XF+ahxpQouchaKbIx4uU6PmKXQTlVqJHoPTMX/lM/tOuSIozz0hziIkGlOgxAVqrGW8NKNHjjb/WPiYaUKLHBGitZrw1oESPN/5a+5hoQIkeE6C1mvHWwH8BSUfSiO3XWNEAAAAASUVORK5CYII=»>

1. Координаты вершины параболы:

1. Точка пересечения с осью OY находится: (0; -5) и ей симметричная.
2. Нанести эти точки на координатную плоскость и построить график параболы:
   2 + 3x — 5 = 0″ height=»671″ src=»https://lh6.googleusercontent.com/TYyA5dFfh0ZKINaPSps3Y_X1mCv8Mhv_8bNG3_dPbZud1AEsvo7UBFmVQNm1GcR1CQFo6HE1lNjYaAgepQUTQiK_ay_Fnuv7LEsB53woHkFO66W0R1PP8QfGsFcYzaR_h4AJdLxC» width=»602″>

Видео:Дробно-линейная функция. 10 класс.Скачать

Уравнение квадратичной функции имеет вид y = a * (x — x₀) 2 + y₀

Координаты его вершины: (x₀; y₀). В уравнении квадратичной функции y = 2x 2 + 3x — 5 при а = 1, то второй коэффициент является четным числом.

Рассмотрим пример: y = 2 * (x — 1) 2 + 4.

Как строим:

1. Воспользуемся линейным преобразованием графиков функций. Для этого понадобится:

• построить y = x 2 ,
• умножить ординаты всех точек графика на 2,
• сдвинуть его вдоль оси ОХ на 1 единицу вправо,
• сдвинуть его вдоль оси OY на 4 единицы вверх.

1. Построить график параболы для каждого случая. 2 + y₀» height=»431″ src=»https://lh5.googleusercontent.com/_zgF-CXWf4Yy0p2OnBYSJkUm0zO-mNetq5feU6LIPEbIgSrO9kdr2ti_tr7Gg3yTMOlJVnuZgG0HleAFfAzG7yr7ELHT6KSMqMrRHkHqt-VcgIiSZx80cVj0zlPMBzEM0wAWQ-L6″ width=»602″>

Видео:Квадратичная функция и ее график. 8 класс.Скачать

Уравнение квадратичной функции имеет вид y = (x + a) × (x + b)

Рассмотрим следующий пример: y = (x − 2) × (x + 1).

Как строим:

Данный вид уравнения позволяет быстро найти нули функции:

(x − 2) × (x + 1) = 0, отсюда х₁ = 2, х₂ = −1.

Определим координаты вершины параболы:

Найти точку пересечения с осью OY:

с = ab = (−2) × (1) = −2 и ей симметричная.

Отметим эти точки на координатной плоскости и соединим плавной прямой.

💡 Видео

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Уравнение с двумя переменными и его график. Алгебра, 9 классСкачать

Графики сложных функций на ОГЭ по математике №22. Подробный разбор основных видов!Скачать

Как решать уравнения с дробью? #shortsСкачать

Дробно-рациональные уравнения. 8 класс.Скачать

Графики сложных функций. Подготовка к ОГЭ. Задание № 22. Вебинар | МатематикаСкачать

5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

Как решать дробно-рациональные уравнения? | МатематикаСкачать

Квадратное уравнение. Модуль. Параметр. График.Скачать

Всё о квадратичной функции. Парабола | Математика TutorOnlineСкачать

Построить график функции (рациональные дроби)Скачать

Задание 23 из ОГЭ Построение графиков функций с модулем | МатематикаСкачать