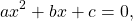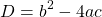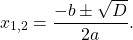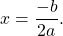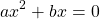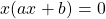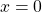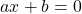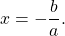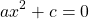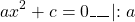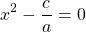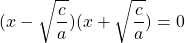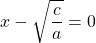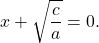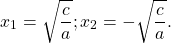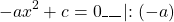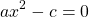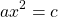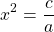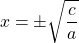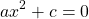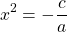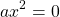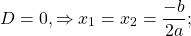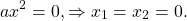теория по математике 📈 уравнения
Уравнение вида ax 2 +bx+c=0, где a,b,c – любые числа, причем a≠0, называют квадратным уравнением. Числа a,b,c принято называть коэффициентами, при этом a – первый коэффициент, b – второй коэффициент, c – свободный член.
Квадратное уравнение может иметь не более двух корней. Решить такое уравнение – это значит найти все его корни или доказать, что их нет.
Видео:Решение квадратных уравнений через сумму коэффициентовСкачать
Дискриминант
Количество корней квадратного уравнения зависит от такого элемента, как дискриминант (обозначают его буквой D).
Нахождение корней квадратного уравнения
Дискриминант – это такой математический инструмент, который позволяет нам определять количество корней. Он выражается определенной формулой:
D=b 2 –4ac
- Если D>0, то уравнение имеет два различных
Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.
Пример №1. Решить уравнение х 2 –2х–3=0. Определяем коэффициенты: а=1, b=–2, c=–3. Находим дискриминант: D=b 2 –4ac=(–2) 2 –41(–3)=4+12=16. Видим, что дискриминант положительный, значит, уравнение имеет два различных корня, находим их:
Пример №2. Решить уравнение 5х 2 +2х+1=0. Определяем коэффициенты: а=5, b=2, c=1. D=b 2 –4ac=2 2 –4=4–20=–16, D 2 –6х+9=0. Определяем коэффициенты: а=1, b=–6, c=9.
D=b 2 –4ac=(–6) 2 –4=36–36=0, D=0, 1
Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.
Видео:Неполные квадратные уравнения. Алгебра, 8 классСкачать
Теорема Виета
Среди квадратных уравнений встречаются такие, у которых первый коэффициент равен 1 (обратим внимание на пример 1 и 3), такие уравнения называются приведенными.
Приведенные квадратные уравнения можно решать не только с помощью дискриминанта, но и с помощью теоремы Виета.
Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком; произведение корней равно третьему коэффициенту.
Корни с помощью данной теоремы находятся устно способом подбора. Рассмотрим это на примерах.
Пример №4. Решить уравнение х 2 –10х+21=0. Выпишем коэффициенты: а=1, b=–10, c=21. Применим теорему Виета:
Начинаем с произведения корней, которое является положительным числом, значит оба корня либо отрицательные, либо положительные. Предполагаем, что это могут быть либо 3 и 7, либо противоположные им числа. Теперь смотрим на сумму, она является положительным числом, поэтому нам подходит пара чисел 3 и 7. Проверяем: 3+7=10, 37=21. Значит, корнями данного уравнения являются числа 3 и 7.
Пример №5. Решить уравнение: х 2 +5х+4=0. Выпишем коэффициенты: а=1, b=5, c=4. По теореме Виета:
Видим, что произведение корней равно 4, значит оба корня либо отрицательные, либо положительные. Видим, что сумма отрицательная, значит, будем брать два отрицательных числа, нам подходят –1 и –4. Проверим:
Данное уравнение является квадратным. Но в его условии присутствует квадратный
Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.
Записываем обязательно в начале решения, что подкоренное выражение может быть только равным нулю или положительным числом (правило извлечения квадратного
Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.
Решаем полученное неравенство: − х ≥ − 5 , отсюда х ≤ 5 . Следовательно, для ответа мы будем выбирать значения, которые меньше или равны 5.
Решаем наше квадратное уравнение, перенося все слагаемые из правой части в левую, изменяя при этом знаки на противоположные и приводя подобные слагаемые (выражения с квадратным корнем взаимоуничтожаются):
х 2 − 2 х + √ 5 − х − √ 5 − х − 24 = 0
Получим приведенное квадратное уравнение, корни которого можно найти подбором по теореме Виета:
х 2 − 2 х − 24 = 0
Итак, корнями уравнения х 2 − 2 х − 24 = 0 будут числа -4 и 6.
Теперь выбираем корень, обращая внимание на наше ограничение на х, т.е. корень должен быть меньше или равен 5. Таким образом, запишем, что 6 – это посторонний корень, так как 6 н е ≤ 5 , а число минус 4 записываем в ответ нашего уравнения, так как − 4 ≤ 5 .
pазбирался: Даниил Романович | обсудить разбор | оценить
Видео:СУММА КОЭФФИЦИЕНТОВ: Как решать Квадратные Уравнения по МАТЕМАТИКЕ 8 классСкачать
Сумма коэффициентов
Скачать
презентацию
Первое свойство коэффициентов. Если сумма коэффициентов равна нулю, т.е. а + b + с = 0, то х1 = 1, х2 = . Доказательство: Разделим обе части уравнения на а, получим приведенное квадратное уравнение Согласно теореме Виета: х1 · х2 = , х1 + х2 = — . По условию, а + в + с = 0, тогда в = — а — с. Значит, х1 · х2 = = 1 · , х1 + х2 = — = — = 1 + . Получаем х1 = 1, х2 = , что и требовалось доказать. Пример 3х2 + 5х – 8 = 0, т.к. а + b + с = 0 ( 3 + 5 – 8 = 0 ), то получим х1 = 1, х2 = = — Ответ: 1 и -. Назад.
Слайд 11 из презентации «Решение уравнений с квадратным корнем» к урокам алгебры на тему «Квадратное уравнение»
Размеры: 960 х 720 пикселей, формат: jpg. Чтобы бесплатно скачать слайд для использования на уроке алгебры, щёлкните на изображении правой кнопкой мышки и нажмите «Сохранить изображение как. ». Скачать всю презентацию «Решение уравнений с квадратным корнем.pptx» можно в zip-архиве размером 257 КБ.
Видео:Квадратные уравнения от «А» до «Я». Классификация, решение и теорема Виета | МатематикаСкачать
Квадратное уравнение
«Нахождение корней квадратного уравнения» — Уравнение корней не имеет. Нахождение корней неполных квадратных уравнений. Способы решения квадратных уравнений. Нахождение дискриминанта. Свойства коэффициентов уравнения. Обратная теорема Виета. Решение неполных квадратных уравнений. Неполные квадратные уравнения. Определение количества корней квадратного уравнения.
«Решение неполных квадратных уравнений» — Постановка учебной задачи. Решение поставленной задачи. Первичное осмысление и применение изученного материала. Считай несчастным тот день или час, в который ты не усвоил ничего. Накопление фактов. Взаимопроверка. Решение неполных квадратных уравнений. Распределите данные уравнения на 4 группы. Вопрос.
«Решение уравнений с квадратным корнем» — Метод выделения полного квадрата. Доказательство. Рисунок. Свободный член приведенного уравнения. Свойства коэффициентов квадратного уравнения. Способы решения квадратных уравнений. Сумма коэффициентов. Уравнение. Приложение. Квадратное уравнение. Разложение на множители. Графическое решение квадратных уравнений.
«Задания по квадратным уравнениям» — Формы решения квадратных уравнений. Цели урока. Квадратные уравнения. Рене Декарт. Команда « Круг». Диофант. Франсуа Виет. Уравнение x2+9=0 имеет два корня. История квадратного уравнения. Команда «Треугольники». Квадратные уравнения в Древнем Вавилоне. Круг. Треугольник. Квадрат. Команда «Квадрат». Энциклопедии по математике для учащихся.
«Математика «Квадратные уравнения»» — М.В. Ломоносов. Решение квадратных уравнений. Цель: научиться видеть рациональный способ решения квадратных уравнений. е) При каком значении а уравнение имеет один корень? Квадратное уравнение aх2+bх+с=0 полное неполное b=0 или c=0. Старайся дать уму как можно больше пищи. Устно решите квадратное уравнение.
«Приёмы решения квадратных уравнений» — Геометрический способ решения квадратных уравнений. Метод выделения полного квадрата. Метод разложения на множители. Квадратные уравнения в Древней Азии. Решение квадратных уравнений. Коэффициент. Приёмы решения. Свойства коэффициентов. Решение квадратных уравнений с помощью номограммы. История развития квадратных уравнений.
Всего в теме «Квадратное уравнение» 34 презентации
Видео:Теорема Виета. 8 класс.Скачать
Квадратное уравнение
Квадратное уравнение — это уравнение вида
где a, b, c — числа, причём a ≠ 0.
Если коэффициенты b и c отличны от нуля, квадратное уравнение называется полным.
Если b или c или оба коэффициента равны нулю, квадратное уравнение называется неполным.
Решение полного квадратного уравнения
Количество корней полного квадратного уравнения зависит от значения дискриминанта.
Дискриминант — это число, вычисляемое по формуле
1) Если D>0, квадратное уравнение имеет два корня, которые находят по формуле
2) Если D=0, квадратное уравнение имеет один корень, который находят по формуле
3) Если D 
Это уравнение типа «произведение равно нулю«. Произведение равно нулю, если хотя бы один из множителей равен нулю. Приравниваем к нулю каждый из множителей:
Таким образом, при c=0 квадратное уравнение имеет два корня, один из которых равен нулю, второй — -b/a.
2) Если b=0
Если знаки a и с разные (например, a>0, c 
Это уравнение — типа «произведение равно нулю». Приравниваем к нулю каждый из множителей:
Если -a 0, обе части уравнения делим на -a
и получаем то же уравнение
Если знаки a и c одинаковые, уравнение не имеет решений.
Если a>0, c>0, то, так как x² — неотрицательное, то ax²≥0 (на самом деле, здесь ax²>0) . Сумма положительных чисел не может равняться нулю, поэтому это уравнение не имеет корней.
Если a 
Таким образом, при b=0 квадратное уравнение либо имеет два корня, которые отличаются только знаками (то есть являются противоположными числами), либо не имеет действительных корней.
3) Если b=0 и c=0
Это уравнение имеет один корень x=0.
Итак, квадратное уравнение может иметь два корня, один корень либо не иметь ни одного корня.
В некоторых источниках один корень рассматривается как два одинаковых корня:
Такие корни называются кратными (второй степени).
В следующий раз для удобства использования запишем виды квадратных уравнений и способы их решения в виде схемы.
Затем рассмотрим примеры решения квадратных уравнений различных видов.
📽️ Видео
5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать
Свойства коэффициентов квадратного уравненияСкачать
ЕГЭ-2018. Задание В-5. Решение квадратного уравнения по сумме коэффициентов.Скачать
Решение квадратных уравнений. Дискриминант. 8 класс.Скачать
Решаем квадратные уравнения как?.. Первый способ - смотрим на сумму коэффициентовСкачать
Формула корней квадратного уравнения. Алгебра, 8 классСкачать
Как решать любое квадратное уравнение Полное Неполное квадр ур x^2+2x-3=0 5x^2-2x=0 2x^2-2=0 3x^2=0Скачать
Решение методом переброски и по сумме коэффициентов ★ 2021x^2-x-2020=0Скачать
Решаем квадратное уравнение с параметромСкачать
СВОЙСТВА КОЭФФИЦИЕНТОВ 😉 #shorts #егэ #огэ #математика #профильныйегэСкачать
коэффициенты в квадратном уравненииСкачать
Квадратные уравнения | Формулы для коэффициентов | АлгебраСкачать
Метод решения квадратного уравнения, зависящий от его коэффициентов. Урок 1Скачать
Квадратные уравнения.Скачать
Алгебра 8. Урок 9 - Квадратные уравнения. Полные и неполныеСкачать
