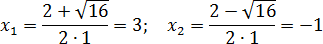Квадратное уравнение когда бесконечное множество решений

В каком случае уравнение ax = b имеет единственный корень; имеет бесконечно много корней; не имеет корней? Приведите примеры.

Решение

Линейное уравнение ax = b при a ≠ 0 имеет один корень, при a = 0 и b ≠ 0, не имеет корней, при a = 0 и b = 0 имеет бесконечно много корней (любое число является его корнем).

Примеры:
15 x = 30 − один корень;
0 x = 4 − не имеет корней;
0 x = 0 − имеет бесконечно много корней.

Нашли ошибку?

Если Вы нашли ошибку, неточность или просто не согласны с ответом, пожалуйста сообщите нам об этом

1. Линейное уравнение. Приведите Примеры линейных уравнений, имеющих один корень, бесконечно много корней и не имеющих корней.

• Попроси больше объяснений
• Следить
• Отметить нарушение

Что ты хочешь узнать?

Видео:Квадратное неравенство. Бесконечное множество решенийСкачать

Ответ

Проверено экспертом

один корень имеют например

5х=6, или 10х=20, или 5х-4=1 или 9х-7=2 и т.д.

бесконечно много корней имеют например 0х=0; 2(5х+6)=10х+12, или 5х-3х-2х=7-4-3

не имеющие корни например 0х=4 или 2х+5=2х+6 и т.д.

После того, как мы изучили понятие равенств, а именно один из их видов – числовые равенства, можно перейти к еще одному важному виду – уравнениям. В рамках данного материала мы объясним, что такое уравнение и его корень, сформулируем основные определения и приведем различные примеры уравнений и нахождения их корней.

Видео:14. Метод Гаусса решения систем линейных уравнений ( бесконечное множество решений ). Часть 3Скачать

Понятие уравнения

Обычно понятие уравнения изучается в самом начале школьного курса алгебры. Тогда оно определяется так:

Уравнением называется равенство с неизвестным числом, которое нужно найти.

Принято обозначать неизвестные маленькими латинскими буквами, например, t , r , m др., но чаще всего используются x , y , z . Иными словами, уравнение определяет форма его записи, то есть равенство будет уравнением только тогда, когда будет приведен к определенному виду – в нем должна быть буква, значение которое надо найти.

Приведем несколько примеров простейших уравнений. Это могут быть равенства вида x = 5 , y = 6 и т.д., а также те, что включают в себя арифметические действия, к примеру, x + 7 = 38 , z − 4 = 2 , 8 · t = 4 , 6 : x = 3 .

После того, как изучено понятие скобок, появляется понятие уравнений со скобками. К ним относятся 7 · ( x − 1 ) = 19 , x + 6 · ( x + 6 · ( x − 8 ) ) = 3 и др. Буква, которую надо найти, может встречаться не один раз, а несколько, как, например, в уравнении x + 2 + 4 · x − 2 − x = 10 . Также неизвестные могут быть расположены не только слева, но и справа или в обеих частях одновременно, например, x · ( 8 + 1 ) − 7 = 8 , 3 − 3 = z + 3 или 8 · x − 9 = 2 · ( x + 17 ) .

Далее, после того, как ученики знакомятся с понятием целых, действительных, рациональных, натуральных чисел, а также логарифмами, корнями и степенями, появляются новые уравнения, включающие в себя все эти объекты. Примерам таких выражений мы посвятили отдельную статью.

В программе за 7 класс впервые возникает понятие переменных. Это такие буквы, которые могут принимать разные значения (подробнее см. в статье о числовых, буквенных выражениях и выражениях с переменными). Основываясь на этом понятии, мы можем дать новое определение уравнению:

Уравнение – это равенство, включающее в себя переменную, значение которой нужно вычислить.

То есть, к примеру, выражение x + 3 = 6 · x + 7 – это уравнение с переменной x , а 3 · y − 1 + y = 0 – уравнение с переменной y .

В одном уравнении может быть не одна переменная, а две и более. Их называют соответственно уравнениями с двумя, тремя переменными и др. Запишем определение:

Уравнениями с двумя (тремя, четырьмя и более) переменными называют уравнения, которые включают в себя соответствующее количество неизвестных.

К примеру, равенство вида 3 , 7 · x + 0 , 6 = 1 является уравнением с одной переменной x , а x − z = 5 – уравнением с двумя переменными x и z . Примером уравнения с тремя переменными может быть выражение x 2 + ( y − 6 ) 2 + ( z + 0 , 6 ) 2 = 26 .

Видео:Решение системы уравнений методом Гаусса. Бесконечное множество решенийСкачать

Корень уравнения

Когда мы говорим об уравнении, сразу возникает необходимость определиться с понятием его корня. Попробуем объяснить, что оно означает.

Нам дано некое уравнение, включающее в себя одну переменную. Если мы подставим вместо неизвестной буквы число, то уравнение станет числовым равенством – верным или неверным. Так, если в уравнении a + 1 = 5 мы заменим букву числом 2 , то равенство станет неверным, а если 4 , то получится верное равенство 4 + 1 = 5 .

Нас больше интересуют именно те значения, с которыми переменная обратится в верное равенство. Они и называются корнями или решениями. Запишем определение.

Корнем уравнения называют такое значение переменной, которое обращает данное уравнение в верное равенство.

Корень также можно назвать решением, или наоборот – оба эти понятия означают одно и то же.

Возьмем пример для пояснения этого определения. Выше мы приводили уравнение a + 1 = 5 . Согласно определению, корнем в данном случае будет 4 , потому что при подстановке вместо буквы оно дает верное числовое равенство, а двойка не будет решением, поскольку ей отвечает неверное равенство 2 + 1 = 5 .

Сколько корней может иметь одно уравнение? Любое ли уравнение имеет корень? Ответим на эти вопросы.

Уравнения, не имеющие ни одного корня, тоже существуют. Примером может быть 0 · x = 5 . Мы можем подставить в него бесконечно много разных чисел, но ни одно из них не превратит его в верное равенство, поскольку умножение на 0 всегда дает 0 .

Также бывают уравнения, имеющие несколько корней. У них может быть как конечное, так и бесконечно большое количество корней.

Так, в уравнении x − 2 = 4 есть только один корень – шесть, в x 2 = 9 два корня ­­– три и минус три, в x · ( x − 1 ) · ( x − 2 ) = 0 три корня – нуль, один и два, в уравнении x=x корней бесконечно много.

Теперь поясним, как правильно записывать корни уравнения. Если их нет, то мы так и пишем: «уравнение корней не имеет». Можно также в этом случае указать знак пустого множества ∅ . Если корни есть, то пишем их через запятую или указываем как элементы множества, заключив в фигурные скобки. Так, если у какого-либо уравнения есть три корня – 2 , 1 и 5 , то пишем – 2 , 1 , 5 или .

Допускается запись корней в виде простейших равенств. Так, если неизвестная в уравнении обозначена буквой y , а корнями являются 2 и 7 , то мы пишем y = 2 и y = 7 . Иногда к буквам добавляются нижние индексы, например, x 1 = 3 , x 2 = 5 . Таким образом мы указываем на номера корней. Если решений у уравнения бесконечно много, то мы записываем ответ как числовой промежуток или используем общепринятые обозначения: множество натуральных чисел обозначается N , целых ­– Z , действительных – R . Скажем, если нам надо записать, что решением уравнения будет любое целое число, то мы пишем, что x ∈ Z , а если любое действительное от единицы до девяти, то y ∈ 1 , 9 .

Когда у уравнения два, три корня или больше, то, как правило, говорят не о корнях, а о решениях уравнения. Сформулируем определение решения уравнения с несколькими переменными.

Решение уравнения с двумя, тремя и более переменными – это два, три и более значения переменных, которые обращают данное уравнение в верное числовое равенство.

Поясним определение на примерах.

Допустим, у нас есть выражение x + y = 7 , которое представляет из себя уравнение с двумя переменными. Подставим вместо первой единицу, а вместо второй двойку. У нас получится неверное равенство, значит, эта пара значений не будет решением данного уравнения. Если же мы возьмем пару 3 и 4 , то равенство станет верным, значит, мы нашли решение.

Такие уравнения тоже могут не иметь корней или иметь бесконечное их количество. Если нам надо записать два, три, четыре и более значений, то мы пишем их через запятую в круглых скобках. То есть в примере выше ответ будет выглядеть как ( 3 , 4 ) .

На практике чаще всего приходится иметь дело с уравнениями, содержащими одну переменную. Алгоритм их решения мы подробно рассмотрим в статье, посвященной решению уравнений.

Видео:Математика| Разложение квадратного трехчлена на множители.Скачать

Когда квадратное уравнение имеет бесконечное множество решений

Что такое линейное уравнение? Что называется корнем линейного уравнения? Сколько корней имеет линейное уравнение? Что значить решить линейное уравнение?

В курсе алгебры 7 класса линейное уравнение определяется следующим образом.

Определение.

Линейное уравнение с одной переменной — это уравнение вида ax=b, где a и b — числа, x — переменная.

Корнем линейного уравнения называется значение переменной, при котором уравнение обращается в верное числовое равенство.

Например, корень уравнения 5x=40 равен 8, так как при x=8 это уравнение превращается в верное числовое равенство:

Количество корней линейного уравнения зависит от значения a (коэффициента перед x).

При a≠0 линейное уравнение имеет единственное решение.

Чтобы найти x, обе части уравнения нужно разделить на число, стоящее перед иксом:

Любое число можно разделить на 2, 5 и числа, которые могут быть представлены в виде произведения только двоек и пятёрок ( например, любое число можно разделить на 10, так как 10=2∙5; на 40, так как 40=2∙2∙2∙5).

В остальных случаях ответ записывают в виде обыкновенной дроби (если дробь неправильная, следует выделить из нее целую часть).

При a=0, b≠0 линейное уравнение

При любом значении x левая часть уравнения равна нулю, а правая — отлична от нуля. То есть нет ни одного значения x, при котором уравнение обратилось бы в верное числовое равенство.

При a=0, b=0 линейное уравнение

имеет бесконечное множество решений.

При любом значении x левая часть уравнения 0x=0 обращается в нуль, в правой части также стоит нуль. Значит, любое число является корнем этого уравнения, то есть, при любом значении x это уравнение обращается в верное числовое равенство.

Возможные решения линейных уравнений можно изобразить в виде схемы.

Решить линейное уравнение — значит, найти корень (корни) уравнения, либо убедиться, что уравнение не имеет корней.

Решение многих уравнений сводится к решению линейных уравнений.

Квадратные уравнения изучают в 8 классе, поэтому ничего сложного здесь нет. Умение решать их совершенно необходимо.

— это уравнение вида ax 2 + bx + c = 0, где коэффициенты a , b и c — произвольные числа, причем a ≠ 0.

Прежде, чем изучать конкретные методы решения, заметим, что все квадратные уравнения можно условно разделить на три класса:

1. Не имеют корней;
2. Имеют ровно один корень;
3. Имеют два различных корня.

В этом состоит важное отличие квадратных уравнений от линейных, где корень всегда существует и единственен. Как определить, сколько корней имеет уравнение? Для этого существует замечательная вещь — дискриминант.

Видео:Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Дискриминант

Пусть дано квадратное уравнение ax 2 + bx + c = 0. Тогда — это просто число D = b 2 − 4 ac .

Эту формулу надо знать наизусть. Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. А именно:

1. Если D D = 0, есть ровно один корень;
2. Если D > 0, корней будет два.

Обратите внимание: дискриминант указывает на количество корней, а вовсе не на их знаки, как почему-то многие считают. Взгляните на примеры — и сами все поймете:

Задача. Сколько корней имеют квадратные уравнения:

1. x 2 − 8 x + 12 = 0;
2. 5 x 2 + 3 x + 7 = 0;
3. x 2 − 6 x + 9 = 0.

Выпишем коэффициенты для первого уравнения и найдем дискриминант:
a = 1, b = −8, c = 12;
D = (−8) 2 − 4 · 1 · 12 = 64 − 48 = 16

Итак, дискриминант положительный, поэтому уравнение имеет два различных корня. Аналогично разбираем второе уравнение:
a = 5; b = 3; c = 7;
D = 3 2 − 4 · 5 · 7 = 9 − 140 = −131.

Дискриминант отрицательный, корней нет. Осталось последнее уравнение:
a = 1; b = −6; c = 9;
D = (−6) 2 − 4 · 1 · 9 = 36 − 36 = 0.

Дискриминант равен нулю — корень будет один.

Обратите внимание, что для каждого уравнения были выписаны коэффициенты. Да, это долго, да, это нудно — зато вы не перепутаете коэффициенты и не допустите глупых ошибок. Выбирайте сами: скорость или качество.

Кстати, если «набить руку», через некоторое время уже не потребуется выписывать все коэффициенты. Такие операции вы будете выполнять в голове. Большинство людей начинают делать так где-то после 50-70 решенных уравнений — в общем, не так и много.

Видео:5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

Корни квадратного уравнения

Теперь перейдем, собственно, к решению. Если дискриминант D > 0, корни можно найти по формулам:

Основная формула корней квадратного уравнения

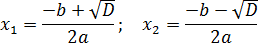
Когда D = 0, можно использовать любую из этих формул — получится одно и то же число, которое и будет ответом. Наконец, если D x 2 − 2 x − 3 = 0;

x 2 + 12 x + 36 = 0.

Первое уравнение:
x 2 − 2 x − 3 = 0 ⇒ a = 1; b = −2; c = −3;
D = (−2) 2 − 4 · 1 · (−3) = 16.

D > 0 ⇒ уравнение имеет два корня. Найдем их:

Второе уравнение:
15 − 2 x − x 2 = 0 ⇒ a = −1; b = −2; c = 15;
D = (−2) 2 − 4 · (−1) · 15 = 64.

D > 0 ⇒ уравнение снова имеет два корня. Найдем их

Наконец, третье уравнение:
x 2 + 12 x + 36 = 0 ⇒ a = 1; b = 12; c = 36;
D = 12 2 − 4 · 1 · 36 = 0.

D = 0 ⇒ уравнение имеет один корень. Можно использовать любую формулу. Например, первую:

Как видно из примеров, все очень просто. Если знать формулы и уметь считать, проблем не будет. Чаще всего ошибки возникают при подстановке в формулу отрицательных коэффициентов. Здесь опять же поможет прием, описанный выше: смотрите на формулу буквально, расписывайте каждый шаг — и очень скоро избавитесь от ошибок.

Видео:Быстрый способ решения квадратного уравненияСкачать

Неполные квадратные уравнения

Бывает, что квадратное уравнение несколько отличается от того, что дано в определении. Например:

Несложно заметить, что в этих уравнениях отсутствует одно из слагаемых. Такие квадратные уравнения решаются даже легче, чем стандартные: в них даже не потребуется считать дискриминант. Итак, введем новое понятие:

Уравнение ax 2 + bx + c = 0 называется , если b = 0 или c = 0, т.е. коэффициент при переменной x или свободный элемент равен нулю.

Разумеется, возможен совсем тяжелый случай, когда оба этих коэффициента равны нулю: b = c = 0. В этом случае уравнение принимает вид a x 2 = 0. Очевидно, такое уравнение имеет единственный корень: x = 0.

Рассмотрим остальные случаи. Пусть b = 0, тогда получим неполное квадратное уравнение вида ax 2 + c = 0. Немного преобразуем его:

Решение неполного квадратного уравнения

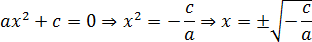
Поскольку арифметический квадратный корень существует только из неотрицательного числа, последнее равенство имеет смысл исключительно при (− c / a ) ≥ 0. Вывод:

1. Если в неполном квадратном уравнении вида ax 2 + c = 0 выполнено неравенство (− c / a ) ≥ 0, корней будет два. Формула дана выше;
2. Если же (− c / a ) c / a ) ≥ 0. Достаточно выразить величину x 2 и посмотреть, что стоит с другой стороны от знака равенства. Если там положительное число — корней будет два. Если отрицательное — корней не будет вообще.

Теперь разберемся с уравнениями вида ax 2 + bx = 0, в которых свободный элемент равен нулю. Тут все просто: корней всегда будет два. Достаточно разложить многочлен на множители:

Вынесение общего множителя за скобку

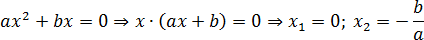
Произведение равно нулю, когда хотя бы один из множителей равен нулю. Отсюда находятся корни. В заключение разберем несколько таких уравнений:

Задача. Решить квадратные уравнения:

x 2 − 7 x = 0 ⇒ x · ( x − 7) = 0 ⇒ x ₁ = 0; x ₂ = −(−7)/1 = 7.

5 x 2 + 30 = 0 ⇒ 5 x 2 = −30 ⇒ x 2 = −6. Корней нет, т.к. квадрат не может быть равен отрицательному числу.

4 x 2 − 9 = 0 ⇒ 4 x 2 = 9 ⇒ x 2 = 9/4 ⇒ x ₁ = 3/2 = 1,5; x ₂ = −1,5.

Хочешь подготовиться к ОГЭ или ЕГЭ по математике на отлично?

Хочешь проверить свои силы и узнать результат насколько ты готов к ЕГЭ или ОГЭ?

Важное замечание!
Если вместо формул ты видишь абракадабру, почисти кэш. Как это сделать в твоем браузере написано здесь: «Как почистить кэш браузера».

За этот урок мы решим 33 квадратных уравнения!

Всех видов, всеми способами.

Ты точно разберешься с этой темой!

И самое главное..

Зачем нужно уметь хорошо и быстро решать квадратные уравнения?

Решение многих других уравнений сводится к решению именно квадратных уравнений!

Будет обидно на экзамене решить какое-нибудь сложное уравнение и запнуться на квадратном.

Потому, давай начнем!

Видео:Решение квадратных неравенств | МатематикаСкачать

Что такое квадратное уравнение?

В термине «квадратное уравнение» ключевым является слово «квадратное» .

Это значит, что в уравнении обязательно должна присутствовать переменная (тот самый икс) в квадрате.

И при этом не должно быть иксов в третьей (и большей) степени.

Если говорить научным, математическим языком, то.

Квадратное уравнение, это уравнение вида

, , – некоторые числа, причем .

и называют коэффициентами квадратного уравнения,

а – свободным членом .

Видео:Система уравнений не имеет решений или имеет бесчисленное множество решенийСкачать

Сначала научимся определять, что перед нами квадратное уравнение, а не какое-нибудь другое

Пример 1

Избавимся от знаменателя и домножим каждый член уравнения на

Перенесем все в левую часть и расположим члены в порядке убывания степеней икса

Теперь можно с уверенностью сказать, что данное уравнение является квадратным!

Пример 2

Домножим левую и правую часть на :

Это уравнение, хотя в нем изначально был , не является квадратным!

Пример 3

Домножим все на :

Страшно? Четвертая и вторая степени… Однако, если произвести замену , то мы увидим, что перед нами простое квадратное уравнение:

Пример 4

Вроде бы есть , но давай посмотрим внимательнее. Перенесем все в левую часть:

Видишь, сократился – и теперь это простое линейное уравнение!

Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Теперь попробуй сам определить, какие из следующий уравнений являются квадратными, а какие нет

Проверь ответы

1. квадратное;
2. квадратное;
3. не квадратное;
4. не квадратное;
5. не квадратное;
6. квадратное;
7. не квадратное;
8. квадратное.

Математики условно делят все квадратные уравнения на вида:

Видео:Решение квадратных неравенств методом интервалов. 8 класс.Скачать

Два вида квадратных уравний — полные и неполные

Полные квадратные уравнения

Полные квадратные уравнения — это уравнения, в которых коэффициенты и , а также свободный член с не равны нулю (как в примере ).

Кроме того, среди полных квадратных уравнений выделяют приведенные – это уравнения, в которых коэффициент (уравнение из примера один является не только полным, но еще и приведенным!)

Неполные квадратные уравнения

Неполные квадратные уравнения – это уравнения, в которых коэффициент и или свободный член с равны нулю:

Неполные они, потому что в них не хватает какого-то элемента.

Но в уравнении всегда должен присутствовать икс в квадрате. Иначе это будет уже не квадратное, а какое-то другое уравнение.

Зачем придумали такое деление? Казалось бы, есть икс в квадрате, и ладно.

Такое деление обусловлено методами решения.

Рассмотрим каждый из них подробнее.

Для начала остановимся на решении неполных квадратных уравнений – они гораздо проще!

Видео:Когда система уравнений имеет бесконечное множество решений .Скачать

Решение неполных квадратных уравнений

Неполные квадратные уравнения бывают типов:

1. , в этом уравнении коэффициент равен .
2. , в этом уравнении свободный член равен .
3. , в этом уравнении коэффициент и свободный член равны .

Теперь рассмотрим решение каждого из этих подтипов.

Поскольку мы знаем, как извлекать квадратный корень, то давайте выразим из этого уравнения

Выражение может быть как отрицательным, так и положительным.

Число, возведенное в квадрат, не может быть отрицательным, ведь при перемножении двух отрицательных или двух положительных чисел – результатом всегда будет положительное число.

Так что: если , то уравнение не имеет решений.

А если 0″> , то получаем два корня . Эти формулы не нужно запоминать. Главное, ты должен знать и помнить всегда, что не может быть меньше .

Давай попробуем решить несколько примеров.

Пример 5

Теперь осталось извлечь корень из левой и правой части. Ведь ты помнишь как извлекать корни?

Ответ:

Никогда не забывай про корни с отрицательным знаком.

Пример 6

Ответ:

Пример 7

Ой! Квадрат числа не может быть отрицательным, а значит у уравнения

Для таких уравнений, в которых нет корней, математики придумали специальный значок – (пустое множество). И ответ можно записать так:

Ответ:

Вынесем общим множитель за скобки:

Произведение равно нулю, если хотя бы один из множителей равен нулю. А это значит, что уравнение имеет решение, когда:

Таким образом, данное квадратное уравнение имеет два корня. Здесь нет никаких ограничений, так как корень мы не извлекали.

Пример 8

Вынесем общий множитель за скобки:

У этого уравнения два корня.

Ответ:

Самый простой тип неполных квадратных уравнений (хотя они все простые, не так ли?). Очевидно, что данное уравнение всегда имеет только один корень:

Здесь обойдемся без примеров.

Видео:15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

Решение полных квадратных уравнений

Напоминаем, что полное квадратное уравнение, это уравнение вида:

Решение полных квадратных уравнений немного сложнее (совсем чуть-чуть), чем приведенных.

Запомни, любое квадратное уравнение можно решить с помощью дискриминанта!

Даже неполное.

Остальные способы помогут сделать это быстрее, но если у тебя возникают проблемы с квадратными уравнениями, для начала освой решение с помощью дискриминанта.

Видео:Система линейных уравнений. Общее решение. Метод ГауссаСкачать

1. Решение квадратных уравнений с помощью дискриминанта.

Решение квадратных уравнений этим способом очень простое, главное запомнить последовательность действий и пару формул.

Если 0″> , то уравнение имеет 2 корня. Нужно особое внимание обратить на шаг 2.

Дискриминант D указывает нам на количество корней уравнения.

Алгоритм

Пример:

Шаг 1. Привести уравнение к стандартному виду:

Если уравнение уже дано в таком виде, то этот шаг делать не нужно.

Главное правильно определить коэффициенты и и свободный член .

Шаг 2. Вычислить дискриминант.

Вот его формула:

Шаг 3. Найти корни уравнения по формуле:

• Если , то формула на шаге сократится до . Таким образом, уравнение будет иметь всего корень.
• Если , то мы не сможем извлечь корень из дискриминанта на шаге . Это указывает на то, что уравнение не имеет корней.

Почему возможно разное количество корней?

Обратимся к геометрическому смыслу квадратного уравнения.

График функции является параболой:

В частном случае, которым является квадратное уравнение, .

А это значит, что корни квадратного уравнения, это точки пересечения с осью абсцисс (ось ).

Парабола может вообще не пересекать ось , либо пересекать ее в одной (когда вершина параболы лежит на оси ) или двух точках.

Кроме того, за направление ветвей параболы отвечает коэффициент . Если 0″> , то ветви параболы направлены вверх, а если – то вниз.

Вернемся к нашим уравнениям и рассмотрим несколько примеров.

Пример 9

Уравнение представлено в стандартном виде, поэтому Шаг 1 пропускаем.

Шаг 2.

0″> , а значит уравнение имеет два корня.

Шаг 3.

Ответ:

Пример 10

Уравнение представлено в стандартном виде, поэтому Шаг 1 пропускаем.

Шаг 2.

, а значит уравнение имеет один корень.

Ответ:

Пример 11

Уравнение представлено в стандартном виде, поэтому Шаг 1 пропускаем.

Шаг 2.

, азначит мы не сможем извлечь корень из дискриминанта. Корней уравнения не существует.

Теперь мы знаем, как правильно записывать такие ответы.

Ответ: Корней нет

Видео:Формула корней квадратного уравнения. Алгебра, 8 классСкачать

2. Решение квадратных уравнений с помощью теоремы Виета

Познакомили поэта с теоремою Виета. Оба корня он сложил, минус он получил. А корней произведенье дает из уравнения.

Если ты помнишь, то есть такой тип уравнений, которые называются приведенными (когда коэффициент а равен ):

Такие уравнения очень просто решать, используя теорему Виета:

Сумма корней приведенного квадратного уравнения равна , а произведение корней равно .

Использовать теорему Виета очень легко.

Нужно всего лишь подобрать такую пару чисел, произведение которых равно свободному члену уравнения, а сумма – второму коэффициенту, взятому с обратным знаком.

Рассмотрим несколько примеров:

Пример 12

Это уравнение подходит для решения с использованием теоремы Виета, т.к. .

Сумма корней уравнения равна , т.е. получаем первое уравнение:

А произведение равно :

Составим и решим систему:

Подберем такие пары чисел, произведение которых равно , и проверим, равна ли их сумма :

• и . Сумма равна ;
• и . Сумма равна ;
• и . Сумма равна .

и являются решением системы:

Таким образом, и – корни нашего уравнения.

Ответ: ; .

Пример 13

Уравнение приведенное, а значит:

Свободный член отрицателен, а значит и произведение корней отрицательно. А это возможно только тогда, когда один корень уравнения отрицателен, а другой положителен.

Подберем такие пары чисел, произведение которых равно , а затем определим, какой корней должен иметь отрицательный знак:

Очевидно, что под первое условие подходят только корни и :

Ответ:

Пример 14

Уравнение приведенное, а значит:

Сумма корней отрицательна, а это значит что, по крайней мере, один из корней отрицателен. Но поскольку их произведение положительно, то значит оба корня со знаком минус.

Подберем такие пары чисел, произведение которых равно :

Очевидно, что корнями являются числа и .

Ответ:

Видео:Решаем квадратное уравнение с параметромСкачать

КВАДРАТНЫЕ УРАВНЕНИЯ. СРЕДНИЙ УРОВЕНЬ

Видео:Комплексные корни квадратных уравнений. 11 класс.Скачать

Что такое квадратное уравнение?

Квадратными называются уравнения, в которых присутствует переменная в квадрате, и при этом нет переменной в степенях, больших .

Другими словами, квадратное уравнение – это уравнение вида , где – неизвестное, , , – некоторые числа, причем .

Число называют старшим или первым коэффициентом квадратного уравнения, – вторым коэффициентом , а – свободным членом .

Потому что если , уравнение сразу станет линейным, т.к. пропадет .

При этом и могут быть равны нулю. В этом стулчае уравнение называют неполным.

Если же все слагаемые на месте, то есть , уравнение – полное.

Видео:Квадратные уравнения от «А» до «Я». Классификация, решение и теорема Виета | МатематикаСкачать

Методы решения неполных квадратных уравнений

Для начала разберем методы решений неполных квадратных уравнений – они проще.

Можно выделить типа таких уравнений:

I. , в этом уравнении коэффициент и свободный член равны .

II. , в этом уравнении коэффициент равен .

III. , в этом уравнении свободный член равен .

Теперь рассмотрим решение каждого из этих подтипов.

Очевидно, что данное уравнение всегда имеет только один корень:

Число, возведенное в квадрат, не может быть отрицательным, ведь при перемножении двух отрицательных или двух положительных чисел результатом всегда будет положительное число. Поэтому:

если , то уравнение не имеет решений;

если 0″> , имеем учаем два корня

Эти формулы не нужно запоминать. Главное помнить, что не может быть меньше .

Примеры решения квадратных уравнений

Пример 15

Никогда не забывай про корни с отрицательным знаком!

Пример 16

Квадрат числа не может быть отрицательным, а значит у уравнения

Чтобы коротко записать, что у задачи нет решений, используем значок пустого множества .

Пример 17

Итак, это уравнение имеет два корня: и .

Вынесем общим множитель за скобки:

Произведение равно нулю, если хотя бы один из множителей равен нулю. А это значит, что уравнение имеет решение, когда:

Итак, данное квадратное уравнение имеет два корня: и .

Разложим левую часть уравнения на множители и найдем корни:

Видео:ФСР. Система однородных уравнений. Общее решениеСкачать

Методы решения полных квадратных уравнений

Видео:ОГЭ математика. Задача 9. Решаем квадратное уравнение методом разложения на множителиСкачать

1. Дискриминант

Решать квадратные уравнения этим способом легко, главное запомнить последовательность действий и пару формул. Запомни, любое квадратное уравнение можно решить с помощью дискриминанта! Даже неполное.

Алгоритм

Пример:

Шаг 1. Привести уравнение к стандартному виду:

Если уравнение уже дано в таком виде, то этот шаг делать не нужно.

Главное правильно определить коэффициенты и и свободный член .

Шаг 2. Вычислить дискриминант. Вот его формула:

Шаг 3. Найти корни уравнения по формуле:

Ты заметил корень из дискриминанта в формуле для корней?

Но ведь дискриминант может быть отрицательным.

Нужно особое внимание обратить на шаг 2. Дискриминант указывает нам на количество корней уравнения.

• Если 0″> , то уравнение имеет корня:
• Если , то уравнение имеет одинаковых корня, а по сути, один корень:

Такие корни называются двукратными.

Почему возможно разное количество корней?

Обратимся к геометрическому смыслу квадратного уравнения. График функции является параболой:

В частном случае, которым является квадратное уравнение, .

А это значит, что корни квадратного уравнения, это точки пересечения с осью абсцисс (ось ).

Парабола может вообще не пересекать ось , либо пересекать ее в одной (когда вершина параболы лежит на оси ) или двух точках.

Кроме того, за направление ветвей параболы отвечает коэффициент . Если 0″> , то ветви параболы направлены вверх, а если – то вниз.

4 примера решения квадратных уравнений

Квадратные уравнения и квадратичные неравенства с параметрами

Дорогой друг! Если ты никогда не решал задач с параметрами – прочитай статьи «Что такое параметр» и «Графический способ решения задач с параметрами». Квадратные уравнения, а тем более неравенства с параметрами только на первый взгляд кажутся простыми. Чтобы уверенно решать их, надо знать определенные приемы. О некоторых мы расскажем.

Разберем сначала подготовительные задачи. А в конце – реальную задачу ЕГЭ.

1. Найдите все значения a, при которых уравнение не имеет действительных корней.

Всегда ли это уравнение является квадратным относительно переменной х? – Нет, не всегда. В случае, когда коэффициент при равен нулю, оно станет линейным.

Рассмотрим два случая – когда это уравнение квадратное и когда оно линейное.

Тогда уравнение примет вид 2 = 0. Такое уравнение не имеет действительных корней, что удовлетворяет условию задачи.

Уравнение будет квадратным. Квадратное уравнение не имеет действительных корней тогда и только тогда, когда его дискриминант отрицательный.

Если и – корни квадратного уравнения
, то по теореме Виета:

Решим первое неравенство системы

Квадратный трехчлен в левой части не имеет корней, так как дискриминант равен -32, то есть отрицателен. Поэтому неравенство будет выполняться для всех действительных значений .

Возведем второе уравнение системы в квадрат:

Из этих двух уравнений выразим сумму квадратов и .

Значит, сумму квадратов корней уравнения можно выразить через параметр

График функции — парабола, ее ветви направлены вверх, минимум будет достигаться в ее вершине. Найдем вершину параболы:

3) Найдите все значения , при каждом из которых все решения уравнения

Как и в первой задаче, уравнение является квадратным, кроме случая, когда . Рассмотрим этот случай отдельно

1) . Получим линейное уравнение

У него единственный корень, причем положительный. Это удовлетворяет условию задачи.

2) При уравнение будет квадратным. Нам надо, чтобы решения существовали, причем были положительными. Раз решения есть, то .

Покажем один из приемов решения квадратичных уравнений и неравенств с параметрами. Он основан на следующих простых утверждениях:

— Оба корня квадратного уравнения и положительны тогда и только тогда, когда их сумма положительна и произведение положительно.

Очевидно, что сумма и произведение двух положительных чисел также положительны. И наоборот – если сумма и произведение двух чисел положительны, то и сами числа положительны.

— Оба корня квадратного уравнения и отрицательны тогда и только тогда, когда их сумма отрицательна, а произведение положительно.

Корни квадратного уравнения и имеют разные знаки тогда и только тогда, когда их произведение отрицательно.

Сумма и произведение корней входят в формулировку теоремы Виета, которой мы и воспользуемся. Получим

Второе и третье неравенства имеют одинаковое решение . Решение первого неравенства:
.

С учетом пункта 1 получим ответ

4. При каких значениях параметра a уравнение

имеет единственное решение?

Уравнение является показательным, причем однородным. Мы умеем решать такие уравнения! Разделим обе части на .

Сделаем замену

Для того, чтобы исходное уравнение имело единственное решение, нужно, чтобы уравнение относительно t имело ровно один положительный корень.

1) В случае уравнение будет линейным

Значит, подходит. В этом случае уравнение имеет единственный положительный корень.

2) Если , уравнение будет квадратным.

Дискриминант является полным квадратом и поэтому всегда неотрицателен. Уравнение имеет либо один, либо два корня. В этом случае несложно найти корни в явном виде.

Один корень получился не зависящим от параметра, причем положительным. Это упрощает задачу.

Для того, чтобы уравнение имело единственный положительный корень, нужно, чтобы либо второй был отрицательным, либо равным нулю, либо чтобы корни совпадали. Рассмотрим все случаи.

Объединив все случаи, получим ответ.

И наконец – реальная задача ЕГЭ.

5. При каких значениях a система имеет единственное решение?

Решением квадратного неравенства может быть:

В каких случаях система двух квадратных неравенств имеет единственное решение:

1) единственная общая точка двух лучей-решений ( или интервалов-решений)

2) одно из неравенств имеет решение – точку, которая является решением второго неравенства

Рассмотрим первый случай.

Если является решением 1 и 2 уравнений, то является решением уравнения (вытекает из второго первое) ⇒ или

Если , при этом система примет вид:

Второй корень первого уравнения:

Второй корень второго первого:

Если , при этом система примет вид:

– бесконечно много решений, не подходит.

Рассмотрим второй случай.

– решением является точка, если – является решением второго неравенства.

– решением является точка, если – не является решением первого неравенства.