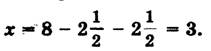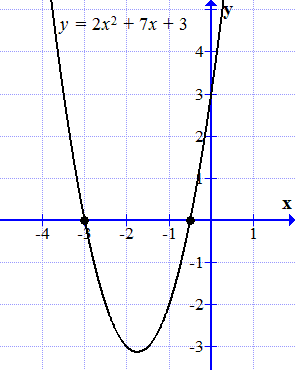Квадратное уравнение и его геометрическая интерпретация

10. СПОСОБ: Геометрический способ решения квадратных уравнений.

В древности, когда геометрия была более развита, чем алгебра, квадратные уравнения решали не алгебраически, а геометрически. Приведу ставший знаменитым пример из «Алгебры» ал — Хорезми.

1) Решим уравнение х 2 + 10х = 39.

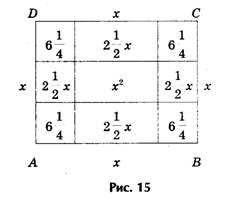
В оригинале эта задача формулируется следующим образом : «Квадрат и десять корней равны 39» (рис.15).

Решение. Рассмотрим квадрат со стороной х, на его сторонах строятся прямоугольники так, что другая сторона каждого из них равна 2,5, следовательно, площадь каждого равна 2,5х. Полученную фигуру дополняют затем до нового квадрата ABCD, достраивая в углах четыре равных квадрата , сторона каждого их них 2,5, а площадь 6,25.

Площадь S квадрата ABCD можно представить как сумму площадей: первоначального квадрата х 2 , четырех прямоугольников (4• 2,5х = 10х ) и четырех пристроенных квадратов (6,25• 4 = 25), т.е. S = х 2 + 10х + 25. Заменяя

х 2 + 10х числом 39, получим, что S = 39 + 25 = 64, откуда следует, что сторона квадрата ABCD, т.е. отрезок АВ = 8. Для искомой стороны х первоначального квадрата получим

2) А вот, например, как древние греки решали уравнение у 2 + 6у — 16 = 0.

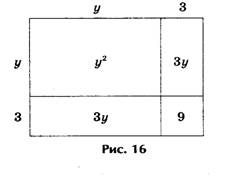
Решение представлено на рис. 16, где

у 2 + 6у = 16, или у 2 + 6у + 9 = 16 + 9.

Решение. Выражения у 2 + 6у + 9 и 16 + 9 геометрически представляют собой один и тот же квадрат, а исходное уравнение у 2 + 6у — 16 + 9 — 9 = 0 — одно и то же уравнение. Откуда и получаем, что у + 3 = ± 5, или у₁ = 2, у₂ = — 8 (рис.16).

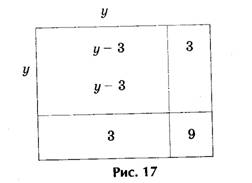
3) Решить геометрически уравнение у 2 — 6у — 16 = 0.

Преобразуя уравнение, получаем

На рис. 17 находим «изображения» выражения у 2 — 6у, т.е. из площади квадрата со стороной у два раза вычитается площадь квадрата со стороной, равной 3. Значит, если к выражению у 2 — 6у прибавить 9, то получим площадь квадрата со стороной у — 3. Заменяя выражение у 2 — 6у равным ему числом 16,

получаем: (у — 3) 2 = 16 + 9, т.е. у — 3 = ± √25, или у — 3 = ± 5, где у₁ = 8 и у₂ = — 2.

Квадратные уравнения находят широкое применение при решении тригонометрических, показательных, логарифмических, иррациональных и трансцендентных уравнений и неравенств.

Однако, значение квадратных уравнений заключается не только в изяществе и краткости решения задач, хотя и это весьма существенно. Не менее важно и то, что в результате применения квадратных уравнений при решении задач не редко обнаруживаются новые детали, удается сделать интересные обобщения и внести уточнения, которые подсказываются анализом полученных формул и соотношений.

Хочется отметить и то, что излагаемая тема в этой работе еще мало изучена вообще, просто ею не занимаются, поэтому она таит в себе много скрытого и неизвестного, что дает прекрасную возможность для дальнейшей работы над ней.

Здесь я остановилась на вопросе решения квадратных уравнений, а что,

если существуют и другие способы их решения?! Опять находить красивые закономерности, какие-то факты, уточнения, делать обобщения, открывать все новое и новое. Но это вопросы уже следующих работ.

Подводя итоги, можно сделать вывод: квадратные уравнения играют огромную роль в развитии математики. Все мы умеем решать квадратные уравнения со школьной скамьи (8 класс), до окончания вуза. Эти знания могут пригодиться нам на протяжении всей жизни.

Так как эти методы решения квадратных уравнений просты в применении, то они, безусловно, должно заинтересовать увлекающихся математикой учеников. Моя работа дает возможность по-другому посмотреть на те задачи, которые ставит перед нами математика.

1. Алимов Ш.А., Ильин В.А. и др. Алгебра, 6-8. Пробный учебник для 6-8 классовой средней школы. — М., Просвещение, 1981.

2. Брадис В.М. Четырехзначные математические таблицы для средней школы.Изд. 57-е. — М., Просвещение, 1990. С. 83.

3. Кружепов А.К., Рубанов А.Т. Задачник по алгебре и элементарным функциям. Учебное пособие для средних специальных учебных заведений. — М., высшая школа, 1969.

4. Окунев А.К. Квадратичные функции, уравнения и неравенства. Пособие для учителя. — М., Просвещение, 1972.

5. Пресман А.А. Решение квадратного уравнения с помощью циркуля и линейки. — М., Квант, № 4/72. С. 34.

6. Соломник В.С., Милов П.И. Сборник вопросов и задач по математике. Изд. — 4-е, дополн. — М., Высшая школа, 1973.

7. Худобин А.И. Сборник задач по алгебре и элементарным функциям. Пособие для учителя. Изд. 2-е. — М., Просвещение, 1970.

Видео:5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

ГЕОМЕТРИЧЕСКОЕ РЕШЕНИЕ КВАДРАТНОГО УРАВНЕНИЯ.

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Описание презентации по отдельным слайдам:

Геометрическое решение квадратного уравнения Автор: Иванова Любовь Алексеевна

Цель: Научить учащихся владению основными способами решения квадратного уравнения Задачи: Изучить историю развития квадратных уравнений. Раскрыть геометрический способ решения квадратных уравнений.

Актуальность работы Квадратные уравнения используются как в учебном процессе, так и для олимпиад самого высокого уровня, а также при решении прикладных задач человеческой жизнедеятельности. Способность ученика подходить к решению уравнений с различных ракурсов, и при этом выбирать наиболее рациональный способ решения, повышает его конкурентоспособность и успешную самореализацию. Квадратные уравнения – «золото» Алгебры.

– это фундамент, на котором покоится величественное здание алгебры. Умение решать квадратные уравнения не только имеет теоретическое значение для познания естественных законов, но и служит практическим целям. Большинство жизненных задач сводится к решению различных видов квадратных уравнений. Квадратное уравнение

История возникновения и развития квадратных уравнений

Кто хочет ограничиться настоящим без знания прошлого, тот никогда его не поймет. Г.В. Лейбниц

решали квадратные уравнения. В древние времена математики ориентировались на человека, его нужды, заботы, возможности. Необходимо было вычислять площади земельных участков, производить расчеты при постройке военных сооружений. В Вавилоне 2 тысячи лет до нашей эры

В VIII столетии до нашей эры в Индии математик Баудхаяма впервые использовал запись квадратных уравнений в виде: и привел методы решения квадратных уравнений

Индийский астроном Ариабхатта

Индийский ученый Брахмагупта (VII век)

Диофант Александрийский (III в.)

«Книга абака» итальянского математика Леонардо Фибоначчи 1201 году

В XVII веке Жирар Декарт систематизировал все теории о квадратных уравнениях.

Геометрический способ решения квадратного уравнения

Пример 1. х2+ 10х -39 = 0 → х2 + 10х = 39 Решение: На сторонах квадрата с ребром х строим прямоугольники 1*х, полученную фигуру дополняем до квадрата ABCD. Площадь квадрата ABCD состоит из площади первоначального квадрата х; площадей десяти прямоугольников 10х и площади квадрата 52 = 25; АВ = х + 5; (х + 5)2 = х2 + 10х + 25 = 39; (х 5)2 = 39 + 25 = 64; х + 5 = ± ± 8; Ответ: х1 = 3; х2 = -13

Пример 2.Решите квадратное уравнение х2 + 6х + 5 = 0 Решение: х2 + 6х = -5; АВ = х + 3; SABCD = (х + 3)2; (х + 3)2 = х2 + 6х = 32; (х + 3)2 = 4; х + 3 = ±2; Ответ: х1 = -1; х2 = -5

Пример 3. Решите квадратное уравнение геометрически 4х2 + 8х – 5 = 0 Решение: 4х2 + 8х = 5; Разделим уравнение на четыре, получим приведенное квадратное уравнение х2 + 2х = ; которое решаем аналогично решениям примеров 1 и 2; х +1 = ± = Ответ: х1 = х2 = — 1

«Опыт научного прошлого не должен быть потерян для будущих поколений, всё развивается по спирали. Человек родился быть господином, повелителем, царем природы. Но мудрость, с которой он должен править с наследственного своего престола, не дана ему от рождения: она приобретается учением».Николай Иванович Лобачевский.

«Торопись, ведь они проходят, Ты у времени в гостях. Не рассчитывай на помощь, Помни: всё в твоих руках!» Юстас Палецкис

«Так, дерзай! Пусть славы эхо о твоих гремит успехах. Станешь ты, хоть скромен вид, знаменитей чем Евклид!» Льюис Керрол

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 930 человек из 80 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 687 человек из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 304 человека из 68 регионов

Ищем педагогов в команду «Инфоурок»

Видео:Квадратные уравнения и геометрическая алгебра древнихСкачать

Дистанционные курсы для педагогов

«Взбодрись! Нейрогимнастика для успешной учёбы и комфортной жизни»

Свидетельство и скидка на обучение каждому участнику

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 593 181 материал в базе

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

«Психологические методы развития навыков эффективного общения и чтения на английском языке у младших школьников»

Свидетельство и скидка на обучение каждому участнику

Другие материалы

• 30.03.2017
• 1047
• 10

• 30.03.2017
• 649
• 0

• 30.03.2017
• 386
• 0

• 30.03.2017
• 1728
• 3

• 30.03.2017
• 1144
• 36

• 30.03.2017
• 256
• 0

• 30.03.2017
• 598
• 4

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 30.03.2017 4164
• PPTX 1.8 мбайт
• 20 скачиваний
• Оцените материал:

Настоящий материал опубликован пользователем Еремова Лена Петровна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 3 года и 1 месяц
• Подписчики: 0
• Всего просмотров: 7590
• Всего материалов: 7

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Квадратные уравнения от «А» до «Я». Классификация, решение и теорема Виета | МатематикаСкачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Курские власти перевели на дистант школьников в районах на границе с Украиной

Время чтения: 1 минута

Ленобласть распределит в школы прибывающих из Донбасса детей

Время чтения: 1 минута

Минпросвещения упростит процедуру подачи документов в детский сад

Время чтения: 1 минута

В Белгородской области отменяют занятия в школах и детсадах на границе с Украиной

Время чтения: 0 минут

Студенты российских вузов смогут получить 1 млн рублей на создание стартапов

Время чтения: 3 минуты

В приграничных пунктах Брянской области на день приостановили занятия в школах

Время чтения: 0 минут

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:Как решать квадратные уравнения. 8 класс. Вебинар | МатематикаСкачать

Корни квадратного уравнения

Видео:Квадратное уравнение. 1 урок.Скачать

Основные формулы

Рассмотрим квадратное уравнение:
(1) .
Корни квадратного уравнения (1) определяются по формулам:
; .
Эти формулы можно объединить так:
.
Когда корни квадратного уравнения известны, то многочлен второй степени можно представить в виде произведения сомножителей (разложить на множители):
.

Далее считаем, что – действительные числа.
Рассмотрим дискриминант квадратного уравнения:
.
Если дискриминант положителен, , то квадратное уравнение (1) имеет два различных действительных корня:
; .
Тогда разложение квадратного трехчлена на множители имеет вид:
.
Если дискриминант равен нулю, , то квадратное уравнение (1) имеет два кратных (равных) действительных корня:
.
Разложение на множители:
.
Если дискриминант отрицателен, , то квадратное уравнение (1) имеет два комплексно сопряженных корня:
;
.
Здесь – мнимая единица, ;
и – действительная и мнимая части корней:
; .
Тогда

.

Видео:Решение биквадратных уравнений. 8 класс.Скачать

Графическая интерпретация

Если построить график функции
,
который является параболой, то точки пересечения графика с осью будут корнями уравнения
.
При , график пересекает ось абсцисс (ось ) в двух точках (см. рисунок ⇓).
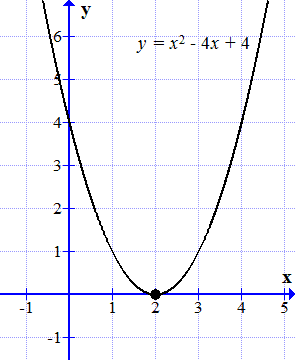
При , график касается оси абсцисс в одной точке (см. рисунок ⇓).
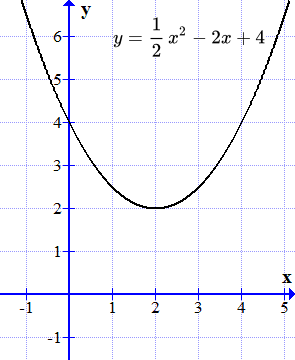
При , график не пересекает ось абсцисс (см. рисунок ⇓).

Видео:Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

Полезные формулы, связанные с квадратным уравнением

Видео:Квадратное уравнение. 8 класс.Скачать

Вывод формулы для корней квадратного уравнения

Выполняем преобразования и применяем формулы (f.1) и (f.3):

,
где
; .

Итак, мы получили формулу для многочлена второй степени в виде:
.
Отсюда видно, что уравнение

выполняется при
и .
То есть и являются корнями квадратного уравнения
.

Видео:8 класс. Квадратное уравнение и его корни. Алгебра.Скачать

Примеры определения корней квадратного уравнения

Пример 1

Найти корни квадратного уравнения:
(1.1) .

Запишем квадратное уравнение в общем виде:
.
Сравнивая с нашим уравнением (1.1), находим значения коэффициентов:
.
Находим дискриминант:
.
Поскольку дискриминант положителен, , то уравнение имеет два действительных корня:
;
;
.

Отсюда получаем разложение квадратного трехчлена на множители:

.

График функции y = 2 x 2 + 7 x + 3 пересекает ось абсцисс в двух точках.

Построим график функции
.
График этой функции является параболой. Она пересевает ось абсцисс (ось ) в двух точках:
и .
Эти точки являются корнями исходного уравнения (1.1).

Пример 2

Найти корни квадратного уравнения:
(2.1) .

Запишем квадратное уравнение в общем виде:
.
Сравнивая с исходным уравнением (2.1), находим значения коэффициентов:
.
Находим дискриминант:
.
Поскольку дискриминант равен нулю, , то уравнение имеет два кратных (равных) корня:
;
.

Тогда разложение трехчлена на множители имеет вид:
.

График функции y = x 2 – 4 x + 4 касается оси абсцисс в одной точке.

Построим график функции
.
График этой функции является параболой. Она касается оси абсцисс (ось ) в одной точке:
.
Эта точка является корнем исходного уравнения (2.1). Поскольку этот корень входит в разложение на множители два раза:
,
то такой корень принято называть кратным. То есть считают, что имеется два равных корня:
.

Пример 3

Найти корни квадратного уравнения:
(3.1) .

Запишем квадратное уравнение в общем виде:
(1) .
Перепишем исходное уравнение (3.1):
.
Сравнивая с (1), находим значения коэффициентов:
.
Находим дискриминант:
.
Дискриминант отрицателен, . Поэтому действительных корней нет.

Можно найти комплексные корни:
;
;
.

График функции не пересекает ось абсцисс. Действительных корней нет.

Построим график функции
.
График этой функции является параболой. Она не пересекает ось абсцисс (ось ). Поэтому действительных корней нет.

Действительных корней нет. Корни комплексные:
;
;
.

Автор: Олег Одинцов . Опубликовано: 19-04-2016

🎬 Видео

Тема: Квадратные уравнения. Урок: Уравнения вида y=ax^2 + bx +cСкачать

Неполные квадратные уравнения. Алгебра, 8 классСкачать

МАТЕМАТИКА 8 класс - Квадратные Уравнения. Как решать Квадратные Уравнения? Формула КорнейСкачать

Алгебра 8. Урок 9 - Квадратные уравнения. Полные и неполныеСкачать

Квадратное уравнение 1. Вводный урокСкачать

Ал-Хорезми и квадратные уравненияСкачать

Квадратные уравнения #shorts Как решать квадратные уравненияСкачать

2. Геометрическая интерпретация комплексных чисел. Модуль и аргумент комплексного числаСкачать

Алгебра 10 класс (Урок№3 - Квадратные уравнения, неравенства и их системы.)Скачать

Быстрый способ решения квадратного уравненияСкачать

Формула корней квадратного уравнения. Алгебра, 8 классСкачать