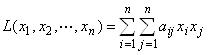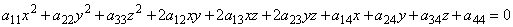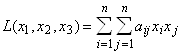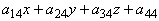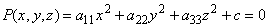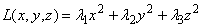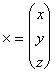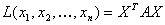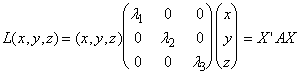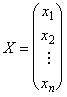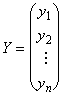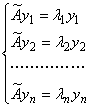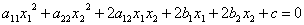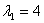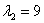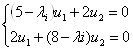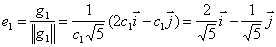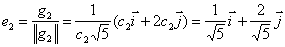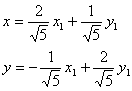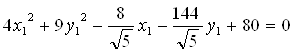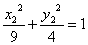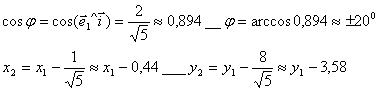Квадратичная форма уравнения 2 го порядка

Видео:Метод Лагранжа. Приведение квадратичной формы к каноническому и нормальному видамСкачать

Приведение кривой второго порядка к каноническому виду

Пример . Дано уравнение кривой 3x 2 +10xy+3y 2 -2x-14y-13=0 в системе координат (0,i,j), где i =(1,0) и j =(0,1).
1. Определить тип кривой.
2. Привести уравнение к каноническому виду и построить кривую в исходной системе координат.
3. Найти соответствующие преобразования координат.

Решение. Приводим квадратичную форму B=3x 2 +10xy+3y 2 к главным осям, то есть к каноническому виду. Матрица этой квадратичной формы . Находим собственные числа и собственные векторы этой матрицы:

Характеристическое уравнение:
; λ₁=-2, λ₂=8. Вид квадратичной формы: .
Исходное уравнение определяет гиперболу.
Заметим, что вид квадратичной формы неоднозначен. Можно записать 8x₁ 2 -2y₁ 2 , однако тип кривой остался тот же – гипербола.
Находим главные оси квадратичной формы, то есть собственные векторы матрицы B. .
Собственный вектор, отвечающий числу λ=-2 при x₁=1: x ₁=(1,-1).
В качестве единичного собственного вектора принимаем вектор , где – длина вектора x ₁.
Координаты второго собственного вектора, соответствующего второму собственному числу λ=8, находим из системы
.
x ₂=(1,1); .
Итак, имеем новый ортонормированный базис ( i ₁, j ₁).
По формулам (5) пункта 4.3.3. переходим к новому базису:
или

Задание. Привести к каноническому виду уравнение линии 17x 2 + 12xy + 8y 2 — 20 = 0.
Решение.Пример 2

Задание. Привести к каноническому виду уравнение линии второго порядка, используя теорию квадратичных форм и определить её вид. Уравнение кривой второго порядка путем выделения полного квадрата привести к каноническому виду. Решение

Задание. Привести уравнение к каноническому виду: 16x 2 — 9y 2 -64x — 8y +199 = 0.
Решение.Скачать решение

Задание. Установить, что каждое из следующих уравнений определяет гиперболу, и найти координаты ее центра С, полуоси, эксцентриситет, уравнения асимптот и уравнения директрис. Изобразить гиперболу на чертеже, указав фокусы, асимптоты и директрисы.
Решение:Скачать решение

Задание. Установить, что каждое из следующих уравнений определяет эллипс, и найти координаты его центра С, полуоси, эксцентриситет, уравнения директрис. Изобразить эллипс на чертеже, указав оси симметрии, фокусы и директрисы.
Решение:Скачать решение

Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Квадратичные формы

Содержание:

Видео:Привести квадратичную форму к каноническому видуСкачать

Квадратичные формы и их определение

Определение. Квадратичной формой L (x₁, x₂, . x_n) от n переменных называется сумма, каждый член которой является или квадратом одной из переменных, или произведением двух различных переменных, взятых с некоторым коэффициентом, то есть
(2.44)

Допускаем, что в квадратичной форме (2.44) a_ij — действительные числа. Распишем квадратичную форму (2.44), разбив слагаемые, содержащие произведения переменных, на две равные части:

Матрица
(2.45)

или A = <a_ij> (i, j = 1, 2, . n) является симметричной, так как a_ij = a_ji, называется матрицей квадратичной формы (2.44).

Рангом квадратичной формы называется ранг ее матрицы. Квадратичная форма называется невырожденной, если ее матрица невырожденная.
Если то квадратичную форму можно переписать в матричном виде L (x₁, x₂, . x_n) = X T AX.

Выражение X T AX представляет собой квадратичную форму в матричном виде.

Пример 1. Записать в матричном виде квадратичную форму

Решение. Матрица данной квадратичной формы имеет вид

А =

Значит,

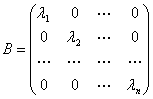
Квадратичная форма называется канонической (или другими словами, имеет канонический вид), если все a_ij = 0, когда i ≠ j. Тогда квадратичная форма будет иметь вид

Рассмотрим следующую теорему.

ТЕОРЕМА 1. Произвольная квадратичная форма приводится к каноническому виду.

Доказательство. Пусть задана квадратичная форма (2.44) с матрицей (2.45) в базисе . Так как A — симметричная матрица, то существует ортогональная матрица B такая, что.

Матрица B является матрицей перехода от базиса
(2.46)
к некоторому базису
. (2.47)

Примечание. Действительная квадратная матрица называется ортогональной, если сумма квадратов элементов каждого столбца равна единице и сумма произведений соответствующих элементов из двух разных столбцов равна нулю. Необходимое и достаточное условие ортогональности матрицы В является условие В T ⋅ B = Е.

Пусть X и Y являются векторами-столбцами из координат вектора соответственно в базисах (2.46) и (2.47). Тогда X = BY и

или
(2.48)

Примечание. При доказательстве данной теоремы использовали транспонирование произведения матриц по формуле (СY) T = Y T ⋅ C T .

Заметим, что в канонической форме (2.48) λ₁, λ₂, . λ_n являются собственными числами матрицы A.

Пример 2. Привести квадратичную форму к каноническому виду с помощью ортогональной матрицы и найти ее.

Решение. Матрица данной квадратичной формы имеет вид . Запишем систему типа (2.39) для нахождения собственных чисел и собственных векторов
(2.49)
Характеристическое уравнение данной системы имеет вид
или (2 – λ) (5 – λ) – 4 = 0.
Решив данное уравнение, находим λ₁ = 6, λ₂ = 1. Значит канонический вид данной квадратичной формы является .
Найдем ортогональную матрицу.

Столбцами ортогональной матрицы, которая приводит квадратичную форму к каноническому виду, является ортонормированный собственные вектор-столбец матрицы A.

Сначала найдем нормированный собственный вектор-столбец матрицы A с собственным значением λ₁ = 6. Для этого из системы (2.49) имеем систему для нахождения координат вектора:

Из данной системы находим x₂ = 2x₁ или u₂ = 2u₁. Значит, при произвольном u₁, отличном от нуля, столбец является собственным вектором-столбиком матрицы A, а столбец является нормированным собственным вектором-столбиком матрицы A. Здесь использовано, что .
Аналогично находим вектор-столбец матрицы A с собственным значением λ₂ = 1, а именно из системы:

Находим x₁ = –2x₂ или при произвольном s, отличном от нуля, столбец является собственным вектором матрицы A. Столбец является нормированным собственным вектором матрицы A. Значит, искомая матрица имеет вид:

Замечание. Легко проверить, что для данного примера 2.
Рассмотрим на примере еще один метод приведения квадратичной формы к каноническому виду.

Метод Лагранжа приведения квадратичной формы к каноническому виду заключается в последовательном выделении полных квадратов.

Пример 3. Привести к каноническому виду квадратичную форму методом Лагранжа. Сначала выделим полный квадрат при переменной x₁, коэффициент при которой отличен от нуля.

Итак, невырожденное линейное преобразование

приводит данную квадратичную форму к каноническому виду

Канонический вид квадратичной формы не является однозначным, так как одна и та же квадратичная форма может быть приведена к каноническому виду многими способами. Однако полученные разными способами квадратичные формы имеют ряд общих свойств.

Сформулируем одно из этих свойств, которое выражает закон инерции квадратичных форм, и заключается в следующем: все канонические формы, к которым приводится данная квадратичная форма, имеют:
1) одно и то же число нулевых коэффициентов;
2) одно и то же число положительных коэффициентов;
3) одно и то же число отрицательных коэффициентов.

Определение 1. Квадратичная форма L (x₁, x₂, . x_n) называется положительно определенной, если для всех действительных значений x₁, x₂, . x_n используется неравенство L (x₁, x₂, . x_n) > 0.

Определение 2. Если L (x₁, x₂, . x_n) является положительно определенной формой, то квадратичная формаL (x₁, x₂, . x_n) T AX была положительно (отрицательно) определенной, необходимо и достаточно, чтобы все собственные значения λ_i (i = 1, 2, . n) матрицы A были положительными (отрицательными).

Данную теорему приводим без доказательства.

Во многих случаях для установления знакоопределенности квадратичной формы удобно применять критерии Сильвестра.

ТЕОРЕМА 3. Для того чтобы квадратичная форма была положительно определенной, необходимо и достаточно, чтобы все главные миноры матрицы этой формы были положительными, то есть
где
Следует заметить, что для отрицательно определенных квадратичных форм знаки главных миноров чередуются, начиная со знака «минус» для минора первого порядка.

Например, квадратичная форма L в примере 2 является положительно определенной на основании теоремы 2, так как корни характеристического уравнения λ₁ = 6 и λ₂ = 1 являются положительными.
Второй способ. Так как главные миноры матрицы A
являются положительными, то по критерию Сильвестра данная квадратичная форма является положительно определенной.

Видео:Приведение ДУ 2 порядка в частных производных к каноническому видуСкачать

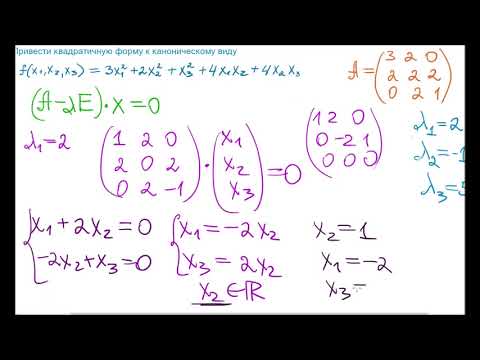
Квадратичные формы

Однородный многочлен второй степени относительно переменных

называется квадратичной формой от этих переменных. Если взять то квадратическую форму (1.26) можно записать в виде:

Выражение (1.28), а следует и квадратичная форма (1.26) полностью определяется матрицей которая называется матрицей квадратичной формы (1.26).

Выполняя замену базиса, квадратичную форму (1.26) можно привести к виду:

где — новые переменные, что линейно выражаются через (1.28), — собственные значения матрицы

Выражение (1.29) называется каноническим видом квадратичной формы (1.26).

Рассмотрим квадратичную форму где — матрица коэффициентов

Тогда квадратичную форму можно записать так:

Квадратичная форма называется положительно определенной, если для всех действительных значений выполняется неравенство и отрицательной, если для всех действительных значений выполняется неравенство

Если положительно определена, то квадратичная форма называется отрицательно определенной.

Решение примеров:

Пример 1.99

является отрицательно определенной.

Пример 1.100

Используя теорию квадратичных форм, привести к каноническому виду уравнения линии второго порядка

Решение. Уравнение линии запишем в виде в котором

Сложим характеристическое уравнение матрицы и найдем ее собственные значения.

или

Корни уравнения являются собственными значениями. Следует, уравнение линии преобразуется в вид или Полученная линия — гипербола.

Свойства квадратичной формы (1.30) связаны с собственными числами матрицы

Пример 1.101

Привести к каноническому виду уравнения линии

Решение. Группа старших членов этого уравнения квадратическую форму Ее матрица

Собственными значениями будут числа Следует квадратичная форма преобразуется к виду а данное уравнение — к виду или Это эллипс.

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Видео:Приведение кривой второго порядка к каноническому виду. ПримерСкачать

69. Квадратичные формы и их приведение к каноническому виду

При рассмотрении евклидового пространства мы вводили определение квадратичной формы. С помощью некоторой матрицы

Строится многочлен второго порядка вида

Который называется квадратичной формой, порождаемой квадратной матрицей А.

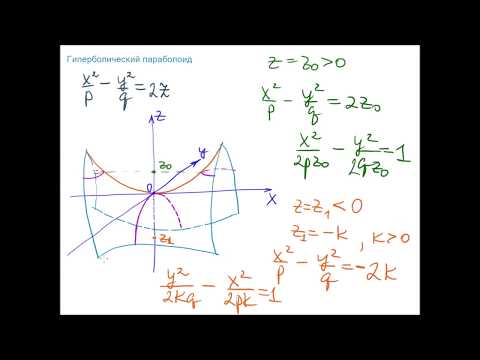
Квадратичные формы тесно связаны с поверхностями второго порядка в n — мерном евклидовом пространстве. Общее уравнение таких поверхностей в нашем трехмерном евклидовом пространстве в декартовой системе координат имеет вид:

Верхняя строка — это не что иное, как квадратичная форма, если положить x1=x, x2=y, x3=z:

— симметричная матрица (aij = aji)

Положим для общности, что многочлен

Есть линейная форма. Тогда общее уравнение поверхности есть сумма квадратичной формы, линейной формы и некоторой постоянной.

Основной задачей теории квадратичных форм является приведение квадратичной формы к максимально простому виду с помощью невырожденного линейного преобразования переменных или, другими словами, замены базиса.

Вспомним, что при изучении поверхностей второго порядка мы приходили к выводу о том, что путем поворота осей координат можно избавиться от слагаемых, содержащих произведение xy, xz, yz или xixj (i¹j). Далее, путем параллельного переноса осей координат можно избавиться от линейных слагаемых и в конечном итоге свести общее уравнение поверхности к виду:

В случае квадратичной формы приведение ее к виду

Называется приведением квадратичной формы к каноническому виду.

Поворот осей координат есть не что иное, как замена одного базиса другим, или, другими словами, линейное преобразование.

Запишем квадратичную форму в матричном виде. Для этого представим ее следующим образом:

L(x, y,z) = x(a11x+a12y+a13z)+

Введем матрицу — столбец

Тогда 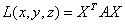— где X T =(x, y,z)

— матричная форма записи квадратичной формы. Эта формула, очевидно, справедлива и в общем случае:

Канонический вид квадратичной формы означает, очевидно, что матрица А имеет диагональный вид:

Рассмотрим некоторое линейное преобразование X = SY, где S — квадратная матрица порядка n, а матрицы — столбцы Х и У есть:

Матрица S называется матрицей линейного преобразования. Отметим попутно, что всякой матрице n-ного порядка при заданном базисе соответствует некоторый линейный оператор.

Линейное преобразование X = SY заменяет переменные x1, x2, x3 новыми переменными y1, y2, y3. Тогда:

где B = S T A S

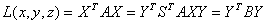
Задача приведения к каноническому виду сводится к отысканию такой матрицы перехода S, чтобы матрица В приобрела диагональный вид:

(*)

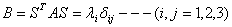
Итак, квадратичная форма с матрицей А после линейного преобразования переменных переходит в квадратичную форму от новых переменных с матрицей В.

Обратимся к линейным операторам. Каждой матрице А при заданном базисе соответствует некоторый линейный оператор А. Этот оператор имеет, очевидно, некоторую систему собственных чисел и собственных векторов. Причем, отметим, что в евклидовом пространстве система собственных векторов будет ортогональна. Мы доказывали на предыдущей лекции, что в базисе собственных векторов матрица линейного оператора имеет диагональный вид. Формула (*), как мы помним, это формула преобразования матрицы линейного оператора при смене базиса. Положим, что собственные вектора линейного оператора А с матрицей А — это вектора у1, y2, . yn.

Т. е.

А это означает, что если собственные вектора у1, y2, . yn взять за базис, то матрица линейного оператора в этом базисе будет диагональной

Или В = S-1 А S, где S – матрица перехода от первоначального базиса <E> к базису <Y>. Причем в ортонормированном базисе матрица S будет ортогональной.

Т. о. для приведения квадратичной формы к каноническому виду необходимо найти собственные числа и собственные векторы линейного оператора А, имеющего в первоначальном базисе матрицу А, которая порождает квадратичную форму, перейти к базису собственных векторов и в новой системе координат построить квадратичную форму.

Обратимся к конкретным примерам. Рассмотрим линии второго порядка.

или

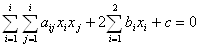
С помощью поворота осей координат и последующего параллельного переноса осей это уравнение можно привести к виду ( переменные и коэффициенты переобозначены х1 = х, х2 = у):

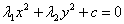
1) если линия центральная, l1 ¹ 0, l2 ¹ 0

2) если линия нецентральная, т. е. один из li = 0.

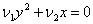
Напомним виды линий второго порядка. Центральные линии:

1) эллипс;

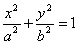
2) гипербола;

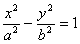
3) точка;

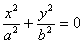
4) две пересекающиеся прямые.

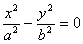
5) х2 = а2 две параллельные линии;

6) х2 = 0 две сливающиеся прямые;

7) у2 = 2рх парабола.

Для нас представляют интерес случаи 1), 2), 7).

Рассмотрим конкретный пример.

Привести к каноническому виду уравнение линии и построить ее:

5х2 + 4ху + 8у2 — 32х — 56у + 80 = 0.

Матрица квадратичной формы есть . Характеристическое уравнение:

Его корни:

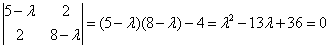
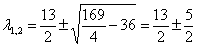
Найдем собственные векторы:

При l1 = 4: 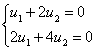u1 = -2u2; u1 = 2c, u2 = — c или g1 = c1(2I – J).

При l2 = 9: 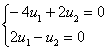2u1 = u2; u1 = c, u2 = 2c или g2 = c2(I+2J).

Нормируем эти векторы:

Составим матрицу линейного преобразования или матрицу перехода к базису g1, g2:

— ортогональная матрица!

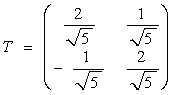
Формулы преобразования координат имеют вид:

или

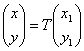
Подставим в наше уравнение линии и получим:

Сделаем параллельный перенос осей координат. Для этого выделим полные квадраты по х1 и у1:

Обозначим . Тогда уравнение приобретет вид: 4х22 + 9у22 = 36 или

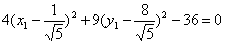
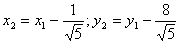
Это эллипс с полуосями 3 и 2. Определим угол поворота осей координат и их сдвиг для того, чтобы построить эллипс в старой системе.

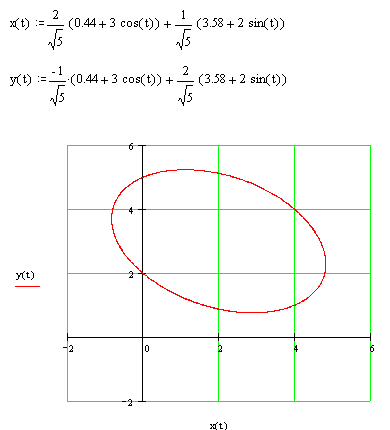
Построим:

Проверка: при х = 0: 8у2 — 56у + 80 = 0 у2 – 7у + 10 = 0. Отсюда у1,2 = 5; 2

При у =0: 5х2 – 32х + 80 = 0 Здесь нет корней, т. е. нет точек пересечения с осью Х!

📽️ Видео

2. Приведение уравнений второго порядка к каноническому видуСкачать

Квадратичные формы. Метод ЛагранжаСкачать

§31.1 Приведение уравнения кривой к каноническому видуСкачать

Приведение квадратичных форм к каноническому видуСкачать

ЛОДУ 2 порядка c постоянными коэффициентамиСкачать

Аналитическая геометрия, 8 урок, Поверхности второго порядкаСкачать

Аналитическая геометрия, 7 урок, Линии второго порядкаСкачать

16. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентамиСкачать

Приведение поверхности второго порядка к каноническому виду ортогональным преобразованием.Скачать

Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

19. Метод вариации произвольных постоянных. Линейные неоднородные диф уравнения 2-го порядкаСкачать

Знакоопределенность квадратичной формыСкачать

Семинар №9 "Приведение уравнения второго порядка к каноническому виду"Скачать

Поверхности второго порядкаСкачать

Видеоурок "Общее уравнение кривой 2 порядка"Скачать