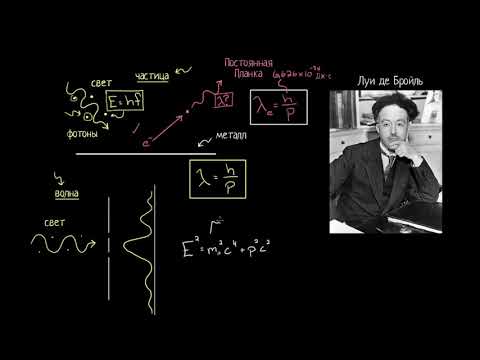
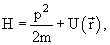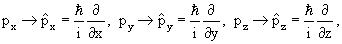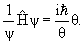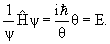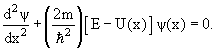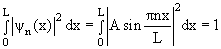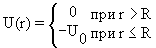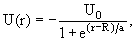Важным этапом в создании квантовой механики явилось обнаружение волновых свойств микрочастиц. Идея о волновых свойствах была первоначально высказана как гипотеза французским физиком Луи де Бройлем.
В физике в течение многих лет господствовала теория, согласно которой свет есть электромагнитная волна. Однако после работ Планка (тепловое излучение), Эйнштейна (фотоэффект) и других стало очевидным, что свет обладает корпускулярными свойствами.
Чтобы объяснить некоторые физические явления, необходимо рассматривать свет как поток частиц-фотонов. Корпускулярные свойства света не отвергают, а дополняют его волновые свойства.
Итак, фотон-элементарная частица света, обладающая волновыми свойствами.
Логично считать, что и другие частицы-электроны, нейтроны- обладают волновыми свойствами.
Формула для импульса фотона
была использована для других микрочастиц массой m, движущихся со скоростью v:
По де Бройлю, движение частицы, например, электрона, подобно волновому процессу с длиной волны λ , определяемой формулой (4.4.3). Эти волны называют волнами де Бройля . Следовательно, частицы (электроны, нейтроны, протоны, ионы, атомы, молекулы) могут проявлять дифракционные свойства.
К.Дэвиссон и Л.Джермер впервые наблюдали дифракцию электронов на монокристалле никеля.
Может возникнуть вопрос: что происходит с отдельными частицами, как образуются максимумы и минимумы при дифракции отдельных частиц?
Опыты по дифракции пучков электронов очень малой интенсивности, то есть как бы отдельных частиц, показали, что при этом электрон не «размазывается» по разным направлениям, а ведет себя как целая частица. Однако вероятность отклонения электрона по отдельным направлениям в результате взаимодействия с объектом дифракции различная. Наиболее вероятно попадание электронов в те места, которые по расчету соответствуют максимумам дифракции, менее вероятно их попадание в места минимумов. Таким образом, волновые свойства присущи не только коллективу электронов, но и каждому электрону в отдельности.
- 4.4.2. Волновая функция и ее физический смысл
- 4.4.3. Соотношение неопределенностей
- 4.4.4.Уравнение Шредингера
- 4.4.5. Применение уравнения Шредингера к атому водорода. Квантовые числа
- Волны (стр. 6 )
- Квадрат модуля волновой функции входящей в уравнение
- 4.1. Уравнение Шредингера
- Уравнение Шредингера
- 4.2. Частица в одномерной прямоугольной яме с бесконечными стенками
- 4.3. Гармонический осциллятор
- Частица в одномерной потенциальной яме
- 4.4. Частица в поле с центральной симметрией
- 4.5. Орбитальный момент количества движения
- 4.6. Спин
- 4.7. Полный момент количества движения
- 4.8. Квантовые числа
- Таблица квантовых чисел
- Задачи
- 🎬 Видео
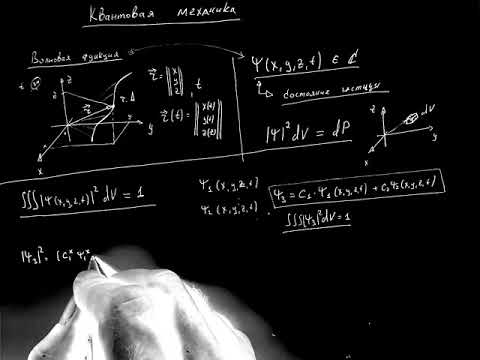
4.4.2. Волновая функция и ее физический смысл
Так как с микрочастицей сопоставляют волновой процесс, который соответствует ее движению, то состояние частиц в квантовой механике описывается волновой функцией, зависящей от координат и времени: .
Если силовое поле, действующее на частицу, является стационарным, то есть не зависящим от времени, то ψ-функцию можно представить в виде произведения двух сомножителей, один из которых зависит от времени, а другой от координат:
В дальнейшем будем рассматривать только стационарные состояния; ψ-функция является вероятностной характеристикой состояния частицы. Поясним смысл этого утверждения.
Выделим в пространстве достаточно малый объем dV=dxdydz, в пределах которого значения ψ-функции можно считать одинаковыми. Вероятность нахождения dW в частицы в этом объеме пропорциональна объему и зависит от квадрата модуля ψ -функции:
Отсюда следует физический смысл волновой функции:
Квадрат модуля волновой функции равен плотности вероятности, то есть отношению вероятности нахождения частицы в объеме к этому объему .
Интегрируя выражение (4.4.5) по некоторому объему V, находим вероятность нахождения частицы в этом объеме:
4.4.3. Соотношение неопределенностей
Одним из важных положений квантовой механики являются соотношения неопределенностей, предложенные В.Гейзенбергом.
Пусть одновременно измеряют положение и импульс частицы, при этом неточности в определениях абсциссы и проекции импульса на ось абсцисс равны соответственно Δx и Δр x .
В классической физике нет каких-либо ограничений, запрещающих с любой степенью точности одновременно измерить как одну, так и другую величину, то есть Δx→0 и Δр x→ 0.
В квантовой механике положение принципиально иное: Δx и Δр x , соответствующие одновременному определению x и р x , связаны зависимостью
Таким образом, чем точнее определена координата x (Δx→0), тем не менее точно определена проекция р x (Δp x→ ± ), и наоборот. Аналогично,
Формулы (4.4.8), (4.4.9) называют соотношениями неопределенностей .
Поясним их одним модельным экспериментом.
При изучении явления дифракции было обращено внимание на то, что уменьшение ширины щели при дифракции приводит к увеличению ширины центрального максимума. Аналогичное явление будет и при дифракции электронов на щели в модельном опыте. Уменьшение ширины щели означает уменьшение Δ x (рис. 4.4.1), это приводит к большему «размазыванию» пучка электронов, то есть к большей неопределенности импульса и скорости частиц.
Рис. 4.4.1.Пояснение к соотношению неопределенности.
Соотношение неопределенностей можно представить в виде
где ΔE — неопределенность энергии некоторого состояния системы; Δt -промежуток времени, в точение которого оно существует. Соотношение (4.4.10) означает, что чем меньше время существования какого-либо состояния системы, тем более неопределенно его значение энергии. Энергетические уровни Е 1 , Е 2 и т.д. имеют некоторую ширину (рис.4.4.2)), зависящую от времени пребывания системы в состоянии, соответствующем этому уровню.
Рис. 4.4.2.Энергетические уровни Е 1 , Е 2 и т.д. имеют некоторую ширину.
«Размытость» уровней приводит к неопределенности энергии ΔE излучаемого фотона и его частоты Δν при переходе системы с одного энергетического уровня на другой:
Это проявляется в уширении спектральных линий.
4.4.4.Уравнение Шредингера
Так как состояние микрочастицы описывают ψ -функцией, то надо указать способ нахождения этой функции с учетом внешних условий. Это возможно в результате решения основного уравнения квантовой механики, предложенного Шредингером. Такое уравнение в квантовой механике постулируется так же, как в классической механике постулируется закон Ньютона.
Применительно к стационарным состояниям уравнение Шредингера может быть записано так:
где m- масса частицы; ; Е и Е n –ее полная и потенциальная энергии (потенциальная энергия определяется силовым полем, в котором находится частица, и для стационарного случая не зависит от времени)
Если частица перемещается только вдоль некоторой линии, например вдоль оси ОХ (одномерный случай), то уравнение Шредингера существенно упрощается и принимает вид
Одним из наиболее простых примеров на использование уравнения Шредингера является решение задачи о движении частицы в одномерной потенциальной яме.
4.4.5. Применение уравнения Шредингера к атому водорода. Квантовые числа
Описание состояний атомов и молекул с помощью уравнения Шредингера является достаточно сложной задачей. Наиболее просто она решается для одного электрона, находящегося в поле ядра. Такие системы соответствуют атому водорода и водородоподобным ионам (однократно ионизированный атом гелия, двукратно ионизированный атом лития и т.п.). Однако и в этом случае решение задачи является сложным, поэтому ограничимся лишь качественным изложением вопроса.
Прежде всего в уравнение Шредингера (4.4.12) следует подставить потенциальную энергию, которая для двух взаимодействующих точечных зарядов – e (электрон) и Ze (ядро), — находящихся на расстоянии r в вакууме, выражается следующим образом:
Состояние электрона в атоме характеризуется не одним, а несколькими квантовыми числами.
Первое из них — главное квантовое число n =1, 2, 3, . Оно определяет уровни энергии электрона по закону
Это выражение является решением уравнения Шредингера и полностью совпадает с соответствующей формулой теории Бора (4.2.30)
На рис.4.4.3 показаны уровни возможных значений полной энергии атома водорода (Е 1 , Е 2 , Е 3 и т.д.) и график зависимости потенциальной энергии Е n от расстояния r между электроном и ядром. С возрастанием главного квантового числа n увеличивается r (см.4.2.26), а полная (4.4.15) и потенциальная энергии стремятся к нулю. Кинетическая энергия также стремится к нулю. Заштрихованная область (Е>0) соответствует состоянию свободного электрона.
Рис. 4.4.3. Показаны уровни возможных значений полной энергии атома водорода
и график зависимости потенциальной энергии от расстояния r между электроном и ядром.
Второе квантовое число – орбитальное l , которое при данном n может принимать значения 0, 1, 2, …., n-1. Это число характеризует орбитальный момент импульса L i электрона относительно ядра:
Третье квантовое число – магнитное m l , которое при данном l принимает значения 0, ±1, ± 2, …, ±l; всего 2l+1 значений. Это число определяет проекции орбитального момента импульса электрона на некоторое произвольно выбранное направление Z:
Четвертое квантовое число – спиновое m s . Оно может принимать только два значения (±1/2) и характеризует возможные значения проекции спина электрона:
Состояние электрона в атоме с заданными n и l обозначают следующим образом: 1s, 2s, 2p, 3s и т.д. Здесь цифра указывает значение главного квантового числа, а буква – орбитальное квантовое число: символам s, p, d, f, соответствуют значения l=0, 1, 2. 3 и т.д.
© ФГОУ ВПО Красноярский государственный аграрный университет, 2015
Видео:Что такое волновая функция? Душкин объяснитСкачать

Волны (стр. 6 )
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 |
I: 20.16; t=0; k=B; ek=50; m=50; c=0;
S: На рисунке представлена диаграмма энергетических уровней атома. Переход с излучением фотона наибольшей частоты обозначен цифрой …
I: 20.17; t=0; k=B; ek=50; m=50; c=0;
S: На рисунке представлена диаграмма энергетических уровней атома. Переход с излучением фотона наименьшей частоты обозначен цифрой …
I: 20.18; t=0; k=B; ek=50; m=50; c=0;
S: На рисунке представлена диаграмма энергетических уровней атома водорода. Поглощение фотона с наибольшей длиной волны происходит при переходе, обозначенном стрелкой под номером …
I: 20.19; t=0; k=B; ek=50; m=50; c=0;
S: На рисунке представлена диаграмма энергетических уровней атома водорода. Поглощение фотона с наименьшей длиной волны происходит при переходе, обозначенном стрелкой под номером …
I: 20.20; t=0; k=B; ek=50; m=50; c=0;
S: На рисунке представлена диаграмма энергетических уровней атома водорода. Излучение фотона с наименьшей длиной волны происходит при переходе, обозначенном стрелкой под номером …
V2: 21. Соотношение неопределенностей Гейзенберга. (B)
I: 21.01; t=0; k=B; ek=50; m=50; c=0;
S: Высокая монохроматичность лазерного излучения обусловлена относительно большим временем жизни электронов в метастабильном состоянии


+:
-:
-:
-:
-:
I: 21.02; t=0; k=B; ek=50; m=50; c=0;
S: Положение пылинки массой 



+:
-:
-:
-:
-:
I: 21.03; t=0; k=B; ek=50; m=50; c=0;
S: Электрон локализован в пространстве в пределах



+:
-:
-:
-:
-:
I: 21.04; t=0; k=B; ek=50; m=50; c=0;
S: Время жизни атома в возбужденном состоянии τ =10 нс. Учитывая, что постоянная Планка 
+:
-:
-:
-:
-:
I: 21.05; t=0; k=B; ek=50; m=50; c=0;
S: Учитывая, что постоянная Планка 

-:
I: 21.06; t=0; k=B; ek=50; m=50; c=0;
S: Определить массу пылинки в килограммах, если ее положение определено с неопределенностью Δх=0,1мкм, а неопределенность скорости 


I: 21.07; t=0; k=B; ek=50; m=50; c=0;
S: Какова неопределенность положения Δх пылинки массой 10-9 кг, если неопределенность скорости 


I: 21.08; t=0; k=B; ek=50; m=50; c=0;
S: Определить пределы локализации в пространстве электрона, если известно, что неопределенность скорости 

I: 21.09; t=0; k=B; ek=50; m=50; c=0;
S: Частица какой массы локализована в пространстве в пределах Δ х = 1 мкм, если неопределенность скорости 

I: 21.10; t=0; k=B; ek=50; m=50; c=0;
S: Определить время жизни атома в возбужденном состоянии, если ширина энергетического уровня составляет не менее 6,6 · 10-8 эВ. Постоянная Планка 
V2: 22. уравнение Шредингера (общие свойства) (A)
I: 22.01; t=0; k=A; ek=25; m=25; c=0;
S: Стационарным уравнением Шредингера для линейного гармонического осциллятора является уравнение …
+:
-:
-:
-:
I: 22.02; t=0; k=A; ek=25; m=25; c=0;
S: Стационарным уравнением Шредингера для частицы в трехмерном ящике с бесконечно высокими стенками является уравнение …
-:
+:
-:
-:
I: 22.03; t=0; k=A; ek=25; m=25; c=0;
S: Стационарным уравнением Шредингера для частицы в одномерном ящике с бесконечно высокими стенками является уравнение …
-:
-:
+:
-:
I: 22.04; t=0; k=A; ek=25; m=25; c=0;
S: Стационарным уравнением Шредингера для электрона в водородоподобном ионе является уравнение …
-:
-:
-:
+:
I: 22.05; t=0; k=A; ek=25; m=25; c=0;
S: Нестационарным уравнением Шредингера является уравнение…
+:
-:
-:
-:
I: 22.06; t=0; k=A; ek=25; m=25; c=0;
S: Стационарное уравнение Шредингера 
+: линейный гармонический осциллятор
-: частицу в трехмерном ящике с бесконечно высокими стенками
-: частицу в одномерном ящике с бесконечно высокими стенками
-: электрон в водородоподобном ионе
I: 22.07; t=0; k=A; ek=25; m=25; c=0;
S: Стационарное уравнением Шредингера 
-: линейный гармонический осциллятор
+: частицу в трехмерном ящике с бесконечно высокими стенками
-: частицу в одномерном ящике с бесконечно высокими стенками
-: электрон в водородоподобном ионе
I: 22.08; t=0; k=A; ek=25; m=25; c=0;
S: Стационарное уравнением Шредингера 
+: частицу в одномерном ящике с бесконечно высокими стенками
-: частицу в трехмерном ящике с бесконечно высокими стенками
-: линейный гармонический осциллятор
-: электрон в водородоподобном ионе
I: 22.09; t=0; k=A; ek=25; m=25; c=0;
S: Стационарное уравнением Шредингера 
+: электрон в водородоподобном ионе
-: частицу в одномерном ящике с бесконечно высокими стенками
-: частицу в трехмерном ящике с бесконечно высокими стенками
-: линейный гармонический осциллятор
I: 22.10; t=0; k=A; ek=25; m=25; c=0;
S: Одномерным временным (нестационарным) уравнением Шредингера является уравнение …
+:
-:
-:
-:
I: 22.11; t=0; k=A; ek=25; m=25; c=0;
S: Для уравнения Шредингера 
1. Уравнение стационарно.
2. Уравнение соответствует трехмерному случаю.
3. Уравнение характеризует состояние частицы в бесконечно глубоком прямоугольном потенциальном ящике.
4. Уравнение характеризует движение частицы вдоль оси Х под действием квазиупругой силы, пропорциональной смещению частицы от положения равновесия.
I: 22.12; t=0; k=A; ek=25; m=25; c=0;
S: С помощью волновой функции 
+: с какой вероятностью частица может быть обнаружена в различных точках пространства
-: импульс частицы в любой точке пространства
-: траекторию, по которой движется частица в пространстве
-: координату частицы в пространстве
I: 22.13; t=0; k=A; ek=25; m=25; c=0;
S: Квадрат модуля волновой функции 
+: плотности вероятности обнаружения частицы в соответствующем месте пространства
-: импульсу частицы в соответствующем месте пространства
-: энергии частицы в соответствующем месте пространства
-: координате частицы в соответствующем месте пространства
I: 22.14; t=0; k=A; ek=25; m=25; c=0;
S: На рисунках приведены картины распределения плотности вероятности нахождения микрочастицы в потенциальной яме с бесконечно высокими стенками. Состоянию с квантовым числом n=2 соответствует
+:
-:
-:
-:
I: 22.15; t=0; k=A; ek=25; m=25; c=0;
S: На рисунках приведены картины распределения плотности вероятности нахождения микрочастицы в потенциальной яме с бесконечно высокими стенками. Состоянию с квантовым числом n=3 соответствует
+:
-:
-:
-:
I: 22.16; t=0; k=A; ek=25; m=25; c=0;
S: На рисунках приведены картины распределения плотности вероятности нахождения микрочастицы в потенциальной яме с бесконечно высокими стенками. Состоянию с квантовым числом n=1 соответствует
+:
-:
-:
-:
I: 22.17; t=0; k=A; ek=25; m=25; c=0;
S: На рисунках приведены картины распределения плотности вероятности нахождения микрочастицы в потенциальной яме с бесконечно высокими стенками. Состоянию с квантовым числом n=4 соответствует
+:
-:
-:
-:
I: 22.18; t=0; k=A; ek=25; m=25; c=0;
S: Задана пси-функция 
+:
-:
-:
-:
I: 22.19; t=0; k=A; ek=25; m=25; c=0;
S: Задана пси-функция 
+:
-:
-:
-:
I: 22.20; t=0; k=A; ek=25; m=25; c=0;
S: Задана пси-функция 

+:
-:
-:
-:
V2: 23. уравнение Шредингера (конкретные свойства) (B)
I: 23.01; t=0; k=B; ek=50; m=50; c=0;
S: Частица находится в потенциальной яме шириной L с бесконечно высокими стенками в определенном энергетическом состоянии 


I: 23.02; t=0; k=B; ek=50; m=50; c=0;
S: Волновая функция вида: 




I: 23.03; t=0; k=B; ek=50; m=50; c=0;
S: Вероятность обнаружить электрон в некотором пространственном интервале определяется через волновую функцию 


+:
-:
-:
-:
-:
I: 23.04; t=0; k=B; ek=50; m=50; c=0;
S: Вероятность обнаружить электрон на участке (a, b) одномерного потенциального ящика с бесконечно высокими стенками вычисляется по формуле 




+:
-:
-:
-:
-:
I: 23.05; t=0; k=B; ek=50; m=50; c=0;
S: Вероятность обнаружить электрон на участке (a, b) одномерного потенциального ящика с бесконечно высокими стенками вычисляется по формуле 




+:
-:
-:
-:
-:
I: 23.06; t=0; k=B; ek=50; m=50; c=0;
S: Вероятность обнаружить электрон на участке (a, b) одномерного потенциального ящика с бесконечно высокими стенками вычисляется по формуле 




+:
-:
-:
-:
-:
I: 23.07; t=0; k=B; ek=50; m=50; c=0;
S: Вероятность обнаружить электрон на участке (a, b) одномерного потенциального ящика с бесконечно высокими стенками вычисляется по формуле 




+:
-:
-:
-:
-:
I: 23.08; t=0; k=B; ek=50; m=50; c=0;
S: Вероятность обнаружить электрон на участке (a, b) одномерного потенциального ящика с бесконечно высокими стенками вычисляется по формуле 




+:
-:
-:
-:
-:
I: 23.09; t=0; k=B; ek=50; m=50; c=0;
S: Вероятность обнаружить электрон на участке (a, b) одномерного потенциального ящика с бесконечно высокими стенками вычисляется по формуле 




+:
-:
-:
-:
Видео:Волновая функция (видео 5) | Квантовая физика | ФизикаСкачать

Квадрат модуля волновой функции входящей в уравнение
Аналог классического волнового уравнения был предложен Э. Шредингером в 1925 г. Как и классическое уравнение, уравнение Шредингера связывает производные волновой функции по времени и координате. Уравнение Шредингера описывает поведение любых нерелятивистских систем. На примерах частицы, находящейся в бесконечно глубокой яме, и гармонического осциллятора рассмотрены простейшие квантовые системы, получены дискретные спектры состояний. Возможности описания динамики данных систем ограничены набором квантовых чисел, отражающих универсальные и внутренние симметрии квантовых систем.
4.1. Уравнение Шредингера
В квантовой физике изменение состояния частицы описывается уравнением Шредингера
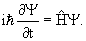 | (4.1) |
где 
в которой 







х → 


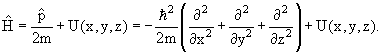 | (4.2) |
Уравнение Шредингера
Зависящее от времени уравнение Шредингера:
где 
Разделение переменных. Запишем Ψ(




Левая часть является функцией только координат, а правая не зависит от переменной x. Поэтому обе части последнего уравнения должны быть равны одной и той же постоянной, которую обозначим E
θ(t) = exp(−iEt/ћ), 




Уравнение 


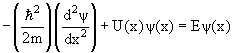
Для трехмерной системы с массой m в поле с потенциалом U(
−(ћ 2 /2m)Δψ(



где Δ – лапласиан.
Так как уравнение Шредингера является линейным уравнением первого порядка по времени, то с его помощью по заданному значению волновой функции Ψ(x, y, z, 0) в момент времени t = 0 можно найти её значение в произвольный момент времени t − Ψ(x, y, z, t).
Уравнение Шредингера для стационарного состояния, когда потенциальная энергия частицы не зависит от времени, имеет вид
 ψ( ψ( ) = Eψ( ) = Eψ( ). ). | (4.3) |
Это уравнение называют стационарным уравнением Шредингера.
Так как в стационарном состоянии
Ψ( ,t) = ψ( ,t) = ψ( )exp(−iEt/ћ) )exp(−iEt/ћ) | (4.4) |
и вероятность найти частицу в момент t в точке x, y, z пропорциональна |Ψ(
|ψ(x,y,z)| 2 , т.е. не зависит от времени. Аналогично, вероятность обнаружить значение физической величины, характеризующей систему, также не изменяется со временем, поскольку выражается через квадрат модуля волновой функции.
4.2. Частица в одномерной прямоугольной яме с бесконечными стенками
Потенциальная энергия U(x) в прямоугольной яме удовлетворяет следующим условиям:
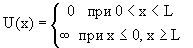 | (4.5) |
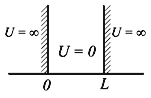
Рис.4.1. Прямоугольная яма с бесконечными стенками
Частица находится в области 0 ≤ x ≤ L. Вне этой области ψ(x) = 0. Уравнение Шредингера для частицы, находящейся в области 0 ≤ x ≤ L
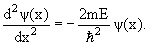 | (4.6) |
Волновая функция, являющаяся решением уравнения (4.9), имеет вид
| ψ(x)= Аsin kx + Bcos kx, | (4.7) |
где k = (2mE/ћ 2 ) 1/2 . Из граничных условий ψ(0) = 0, ψ(L) = 0 и условий непрерывности волновой функции следует
| Аsin kL = 0. | (4.8) |
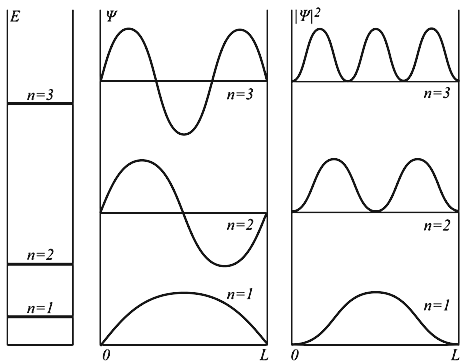
kL = nπ, n = 1, 2, 3, … , то есть внутри потенциальной ямы с бесконечно высокими стенками устанавливаются стоячие волны, а энергия состояния частиц имеет дискретный спектр значений En
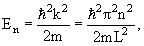 n = 1, 2, 3, … n = 1, 2, 3, … | (4.9) |
Частица может находиться в каком-то одном из множества дискретных состояний, доступных для неё.
Каждому значению энергии En соответствует волновая функция ψn(x), которая с учетом условия нормировки
 | (4.10) |
В отличие от классической, квантовая частица в прямоугольной яме не может иметь энергию
E 2 π 2 /(2mL 2 ). Состояния частицы ψn в одномерном поле бесконечной потенциальной ямы полностью описывается с помощью одного квантового числа n. Спектр энергий дискретный.
Рис. 4.2. Уровни энергии и волновые функции частицы Ψ в бесконечной прямоугольной яме. Квадрат модуля волновой функции |Ψ| 2 определяет вероятность нахождения частицы в различных точках потенциальной ямы.
4.3. Гармонический осциллятор
Положение уровней частицы в потенциальной яме зависит от вида потенциальной ямы. В одномерной потенциальной яме гармонического осциллятора потенциальная энергия имеет вид
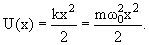 | (4.11) |
В этом случае одномерное уравнение Шредингера имеет вид
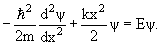 | (4.12) |
Допустимые значения полной энергии определяются формулой
| En = ћω0(n + 1/2), n = 0, 1, 2, | (4.13) |
В отличие от бесконечной прямоугольной ямы, спектр уровней гармонического осциллятора эквидистантный.
С увеличением массы частицы или размеров области ее локализации квантовое описание частицы переходит в классическое.
Частица в одномерной потенциальной яме
Одномерная прямоугольная яма шириной L:
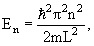

Одномерный гармонический осциллятор:
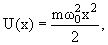
4.4. Частица в поле с центральной симметрией
В сферических координатах стационарное уравнение Шредингера для частицы в центральном потенциале U(r) имеет вид
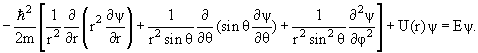 | (4.14) |
Решение уравнения (4.14) записываются в виде произведения радиальной и угловой функций
| ψ(r,θ,φ) = Rnl(r)Ylm(θ,φ), | (4.15) |
где радиальная функция Rnl(r) и угловая функция Ylm(θ,φ), называемая сферической, удовлетворяют уравнениям
 2 Ylm(θ,φ) = ћ 2 l(l +1)Ylm(θ,φ) 2 Ylm(θ,φ) = ћ 2 l(l +1)Ylm(θ,φ) | (4.16) |
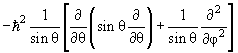 Ylm(θ,φ) = ћ 2 l(l +1)Ylm(θ,φ) Ylm(θ,φ) = ћ 2 l(l +1)Ylm(θ,φ) 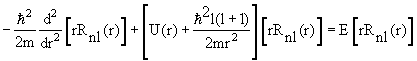 | (4.17) |
Уравнение (4.16) определяет возможные собственные значения l и собственные функции Ylm(θ,φ) оператора квадрата момента 
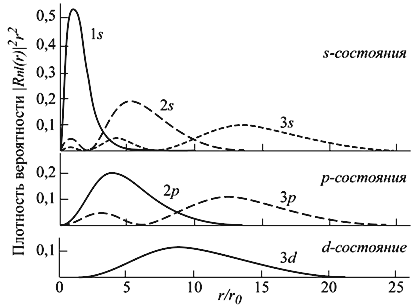
Схема уровней (последовательность и абсолютные значения энергий) зависит от радиальной функции Rnl(r), которая в свою очередь определяется потенциалом U(r), в котором находится частица.
Рис. 4.3. Радиальное распределение вероятности нахождения электрона в кулоновском поле протона (атом водорода). Расстояния даны в боровских радиусах
r0 = ћ 2 /mee 2 ≈ 0.529·10 8 cм.
| Решения уравнения |
существуют лишь при определенных значениях квантовых чисел n (радиальное квантовое число), l (орбитальное квантовое число) и m (магнитное квантовое число).
Возможные энергетические состояния системы (уровни энергии) определяются числами n и l и в случае сферически симметричных состояний не зависят от квантового числа m. Число n может быть только целым:
n = 1, 2, …, ∞. Число l может принимать значения 0, 1, 2, …, ∞.
4.5. Орбитальный момент количества движения
Собственные значения L 2 и Lz являются решением уравнений


Они имеют следующие дискретные значения
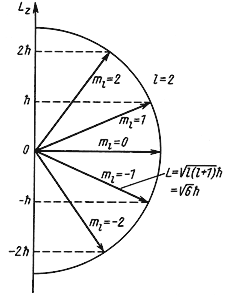
L 2 = ћ 2 l(l + 1), где l = 0, 1, 2, 3, …,
Lz = ћm, где m = 0, ± 1, ± 2, ± 3,…, ± l.
Для характеристики состояний с различными значениями орбитального момента l обычно используют следующие обозначения:
Спектроскопические названия орбитальных моментов l
| l = 0 | s-состояние |
| l = 1 | p-состояние |
| l = 2 | d-состояние |
| l = 3 | f-состояние |
| l = 4 | g-состояние |
| l = 5 | h-состояние |
| и. т. д. |
Состоянию с l = 0 отвечает сферически симметричная волновая функция. В тех случаях, когда l ≠ 0 волновая функция не имеет сферической симметрии. Симметрия волновой функции определяется симметрией сферических функций Ylm(θ,φ). Имеет место интересное квантовое явление, когда решение сферически симметричной задачи (потенциал описывает сферически симметричную систему) приводит к состояниям, не обладающим сферической симметрией. Таким образом, симметрия уравнений не обязательно должна отражаться в симметрии каждого отдельно взятого решения этих уравнений, а лишь во всей совокупности этих решений.
Для частицы, находящейся в сферически симметричном потенциале, величина орбитального момента количества движения L:
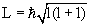 | (4.18) |
Обычно, для упрощения, когда говорят о величине орбитального момента количества движения, называют этой величиной квантовое число l, имея в виду, что между l и L имеется однозначная связь (4.18).
Рис. 4.4 Возможные ориентации вектора 
Так как величина l может принимать только целочисленные значения 0, 1, 2, 3,…, то и орбитальный момент количества движения L квантуется. Например, для частицы с l = 2 момент количества движения
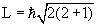
= 6.58·10 -22 √6 МэВ·сек ≈ 2.6·10 — 34 Дж·сек.
Пространственное квантование. Орбитальный момент количества движения является векторной величиной. Так как величина орбитального момента количества движения квантуется, то и направление 

Состояние частицы, находящейся в сферически симметричном поле, полностью описывается тремя квантовыми числами: n, l и m.
Появление квантовых чисел связано со свойствами симметрии системы. Характер этой симметрии определяет возможные значения квантовых чисел. Очевидно, что система, описываемая функцией e im φ , примет прежнее значение только тогда, когда азимутальный угол φ в результате поворота вокруг оси z примет прежнее значение φ. Этому условию функция e im φ удовлетворяет только в случае, когда величина mφ кратна 2π. Т.е. величина m должна иметь целые значения. Так как необходимо учитывать вращение в двух противоположных направлениях и отсутствие вращения, единственно возможными значениями оказываются m = 0, ±1, ±2, … .
4.6. Спин
Спин − собственный момент количества движения частицы. Между значением вектора спина 

 2 = ћ 2 s(s + 1) 2 = ћ 2 s(s + 1) | (4.19) |
В отличие от орбитального квантового числа l, которое может быть лишь целым числом или нулем, спиновое квантовое число s (в дальнейшем просто спин) может быть как целым (включая нуль), так и полуцелым, т. е. s = 0, 1/2, 1, 3/2, 2, 5/2, … , но при этом для каждой элементарной частицы спин может принимать единственное присущее этому типу частиц значение. Так, спины π-мезонов и К-мезонов равны 0. Спины электрона, протона, нейтрино, кварков и их античастиц равны 1/2. Спин фотона равен 1. Бозоны составляют класс частиц с целым значением спина, спин фермионов имеет полуцелое значение. Спин частицы невозможно изменить, также как её заряд или массу. Это её неизменная квантовая характеристика.
Как и в случае других квантовых векторов, проекция вектора спина 
szћ = ±sћ, ±(s − 1)ћ, ±(s − 2)ћ. ±1/2ћ или 0.
Число sz − это квантовое число проекции спина. Максимальная величина sz совпадает с s. Так как спин электрона равен 1/2, то проекция этого спина может принимать лишь два значения sz = ±1/2. Если проекция +1/2, то говорят, что спин направлен вверх, если проекция -1/2, то говорят, что спин направлен вниз.
4.7. Полный момент количества движения
Полный момент количества движения частицы или системы частиц 





Квадрат полного момента имеет значение:

Квантовое число полного момента j, соответствующее сумме двух векторов 

j = l + s, l + s −1. |l − s|
Проекция 
Число значений проекции Jz равно 2j + 1. Если для 

4.8. Квантовые числа
Квантовые числа – это целые или дробные числа, которые определяют все возможные значения физической величины, характеризующей различные квантовые системы – атомы, атомные ядра, кварки и другие частицы.
Таблица квантовых чисел
| n | Радиальное квантовое число. Определяет число узлов волновой функции и энергию системы. n = 1, 2, …, ∞. |
| J, j | Полный угловой момент J и его квантовое число j. Последнее никогда не бывает отрицательным и может быть целым или полуцелым в зависимости от свойств рассматриваемой системы.  2 = ћ 2 j(j + 1). 2 = ћ 2 j(j + 1). |
| L, l | Орбитальный угловой момент L и его квантовое число l. Интерпретация l такая же, как j, но l может принимать только целые значения, включая нуль: l = 0, 1, 2,…. L 2 = ћ 2 l(l + 1). |
| m | Магнитное квантовое число. Проекция полного или орбитального углового момента на выделенную ось (обычно ось z) равна mћ. Для полного момента m = ±j, ±(j-1), …, ±1/2 или 0. Для орбитального m = ± l, ± (l-1), …, ±1, 0. |
| S, s | Спиновый угловой момент S и его квантовое число s. Оно может быть либо положительным целым (включая нуль), либо полуцелым. s – неизменная характеристика частицы определенного типа. S 2 = ћ 2 s(s + 1). |
| sz | Квантовое число проекции спинового момента частицы на выделенную ось. Эта проекция может принимать значения szћ, где sz = ± s, ± (s -1), …, ±1/2 или 0. |
| P или π | Пространственная четность. Характеризует поведение системы при пространственной инверсии  → — → —  (зеркальном отражении). Полная четность частицы Р = π(-1) l , где π – её внутренняя четность, а (-1) l – её орбитальная четность. Внутренние четности кварков положительные, антикварков — отрицательные. (зеркальном отражении). Полная четность частицы Р = π(-1) l , где π – её внутренняя четность, а (-1) l – её орбитальная четность. Внутренние четности кварков положительные, антикварков — отрицательные. |
| I | Изоспин. Характеризует свойство зарядовой инвариантности сильных взаимодействий |
Для обозначения спинового момента часто используют букву J.
Все состояния, в которых может находиться квантовая система, описываются с помощью полного набора квантовых чисел. Так в случае протона в ядре состояние протона описывается с помощью четырех квантовых чисел, соответствующих четырем степеням свободы – трем пространственным координатам и спину. Это
- Радиальное квантовое число n ( 1, 2, …, ∞),
- Орбитальное квантовое число l (0, 1, 2, …),
- Проекция орбитального момента m (± l, ± (l-1), …, ±1, 0),
- Спин протона s =1/2.
Для описания сферически-симметричных систем в квантовой физике используются различные сферически симметричные потенциалы с различной радиальной зависимостью:
- Кулоновский потенциал U = Q/r,
- Прямоугольная потенциальная яма
- Потенциал типа гармонического осциллятора U = kr 2 ,
- Потенциал Вудса-Саксона (с его помощью описываются внутриядерные взаимодействия):
где U0, а и R – положительные константы (R – радиус ядра). Во всех случаях сферически симметричные системы можно описать с помощью набора квантовых чисел n, l, j, jz, однако, в зависимости от радиального вида потенциала энергетический спектр состояний системы будет различным.
Существование сохраняющихся во времени физических величин тесно связано со свойствами симметрии гамильтониана системы. Например, в случае, если квантовая система обладает центральной симметрией U = U(r), то этой системе соответствует сохранение орбитального момента количества движения l и одной из его проекций m. При этом из-за сферической симметрии задачи энергия состояний не будет зависеть от величины m, т. е. состояния будут вырожденными по m.
Наряду с пространственными симметриями, связанными с непрерывными преобразованиями, в квантовой физике существуют и другие симметрии – дискретные. Одной из них является зеркальная симметрия волновой функции относительно инверсии координат (

Система тождественных частиц характеризуется еще одной симметрией – симметрией относительно перестановок тождественных частиц. Эта симметрия определяется свойствами частиц, образующих систему. Системы частиц с целым спином (бозонов) описываются симметричными волновыми функциями, системы частиц с полуцелым спином (фермионов) − антисимметричными волновыми функциями.
Задачи
4.1. Вычислите допустимые уровни энергии электрона, находящегося в одномерной прямоугольной потенциальной яме шириной 10 -8 см, протона, находящегося в потенциальной яме 5 Фм, и шарика массой 1 г, находящегося в потенциальной яме 1 см.
4.2. Рассчитать энергию перехода между состояниями 1s и 2s в атоме водорода.
4.3. Найти значение полного момента j для протона в d-состоянии. Каким будет результат измерения полного момента протона в состоянии 1d5/2?
4.4. Найти полный момент (квантовое число j) системы двух нуклонов в s‑состоянии (l = 0).
4.5. Какие значения может иметь полный момент системы j, если
А. Нейтрон и протон находятся в состояниях с |l,s:j>n = |1, 1 /2: 3 /2>, |l,s:j>p = |1, 1 /2: 3 /2>?
Б. Два нейтрона находятся в состояниях с |l,s:j>1 = |1, 1 /2: 3 /2> и |l,s:j>2 = |1, 1 /2: 3 /2>?
4.6. А) Нейтрон находится в p-состоянии. Найти значения полного момента j и возможные значения проекции момента jz. Каким будет результат измерения орбитального момента частицы в этом состоянии? Б) Рассмотрите задачу А) для протона в d-состоянии.
Ответ: А) j = 3/2, 1/2; jz = ±3/2, ±1/2; L = ћ√ l(l +1) = √ 2 ћ;
Б) j = 5/2, 3/2; jz = ±5/2, ±3/2, ±1/2; L = ћ√ l(l +1) = √ 6 ћ
4.7. А) Частица с собственным моментом s = 3/2 находится в состоянии с орбитальным моментом
l = 2. Найти полный момент частицы j.
Б) Частица с собственным моментом s = 1/2 находится в состоянии с орбитальным моментом
l = 3. Определите полный момент частицы j
Ответ: А) j = 7/2 ÷ 1/2; Б) j = 7/2, 5/2
4.8. Протон и нейтрон находятся в состоянии с относительным орбитальным моментом L = 1. Найти полный момент системы J.
Ответ: J = 0, 1, 2
4.9. На оболочке с квантовым числом n = 1, l = 2 находятся протон и нейтрон. Определить их суммарный полный момент J и его проекцию Jz. Изменится ли результат, если на оболочке n = 1,
l = 2 будут находиться два нейтрона?
4.10. Почему возникают вырожденные состояния?
4.11. Написать оператор Гамильтона 
4.12. Напишите стационарное уравнение Шредингера в сферической системе координат.
4.13. Какие квантовые числа характеризуют частицу в центрально-симметричной потенциальной яме?
4.14. Покажите, что волновые функции ψ = Aexp(kx −ωt) и ψ = Asin(kx −ωt) не удовлетворяют зависящему от времени уравнению Шредингера.
4.15. Покажите, что волновые функции ψ = Ae i(kx −ωt) и ψ = A(cos(kx −ωt) − sin(kx −ωt))удовлетворяют зависящему от времени уравнению Шредингера.
4.16. Частица находится в низшем состоянии n = 1 в бесконечно глубокой одномерной прямоугольной потенциальной яме размера L.
А) Рассчитайте вероятность обнаружить частицу в интервале Δx = 0.001L при x = 1 /2L, x = 2 /3L, x = L.
Б) Рассмотрите случай, когда частица находится в состоянии n = 2 при тех же значениях x.
Ответ: А) P(L/2) = 0.002; P(2L/3) = 0.0015; P(L) = 0; Б) P(L/2) = 0; P(2L/3) = 0.0015; P(L) = 0
4.17. Частица находится в состоянии n = 2 в бесконечно глубокой одномерной прямоугольной потенциальной яме размера L. Рассчитайте вероятность обнаружить частицу в интервале ( 1 /3L, 2 /3L).
Ответ: P(L/3, 2L/3) = 0.2
4.18. Электрон находится всостонии n = 5 в бесконечно глубокой одномерной прямоугольной потенциальной яме размера L. Рассчитайте вероятность обнаружить электрон в области x от 0.2L до 0.5L.
Ответ: P(0.2L, 0.5L) = 0.3
4.19. Электрон находится в бесконечно глубокой одномерной потенциальной яме. Рассчитайте ширину потенциальной ямы, если энергия состояния n = 1 равна 0.1 эВ.
Ответ: L = 1.9 нм
4.20. Рассчитайте средние значения и 2 > для состояний n = 1, 2, 3 в бесконечно глубокой прямоугольной потенциальной яме.
4.21. Что общего и в чем различие в описании атома водорода в теории Шредингера и в модели Бора?
4.22. Почему энергии атома водорода в теории Шредингера не зависят от орбитального квантового числа l?
4.23. Угловой момент характеризуется квантовым числом l = 3. Какие значения могут принимать Lz и L 2 ?
Ответ: Lz = -3ћ, -2ћ. 3ћ; L 2 = 12ћ 2
4.24. Угловой момент характеризуется квантовым числом l = 3. Какие значения могут принимать Lz и L 2 ?
🎬 Видео
Урок 454. Понятие о волновой функцииСкачать

Урок 455. Уравнение ШрёдингераСкачать

Консультация по квантовой механике. Часть 5. "Волновая функция. Уравнение Шредингера"Скачать

Лекции 5-6. Уравнение Шредингера и его приближенные решения. Межатомные.Скачать

Операторы. Волновая функция.Скачать

Лекция №4 "Волновая функция. Уравнение Шредингера" (Гавриков А.В.)Скачать

Теория Бора. Гипотеза де Бройля. Принцип неопределенности. Уравнение Шрёдингера.Скачать

Простое объяснение квантовой волновой функции с канала DoSСкачать
Квантовая механика 49 - Реальна ли волновая функция?Скачать

QM_01 (Волновая функция)Скачать
Волновые функции электрона в водородоподобном атомеСкачать

Петров С.В. - Квантовая механика - 4. Свойства и элементы пространства волновой функцииСкачать
Структура материи 6: уравнение Шрёдингера. Зачем нужна квантовая механика – Виталий Бейлин | НаучпопСкачать

Квантовая механика. Основа реальности часть 1. Волновая функция.Скачать

97. Микрочастица в потенциальной ямеСкачать

Что такое коллапс волновой функции? Душкин объяснитСкачать

Волна де Бройля (видео 4) | Квантовая физика | ФизикаСкачать
Уравнение ШрёдингераСкачать