Куб суммы куб разности уравнения (8 видео)

Куб суммы и разности двух выражений

Содержание

Формула куба суммы
Формула куба разности
Примеры
Алгебра. 7 класс
Сокращенное умножение: правила, формулы
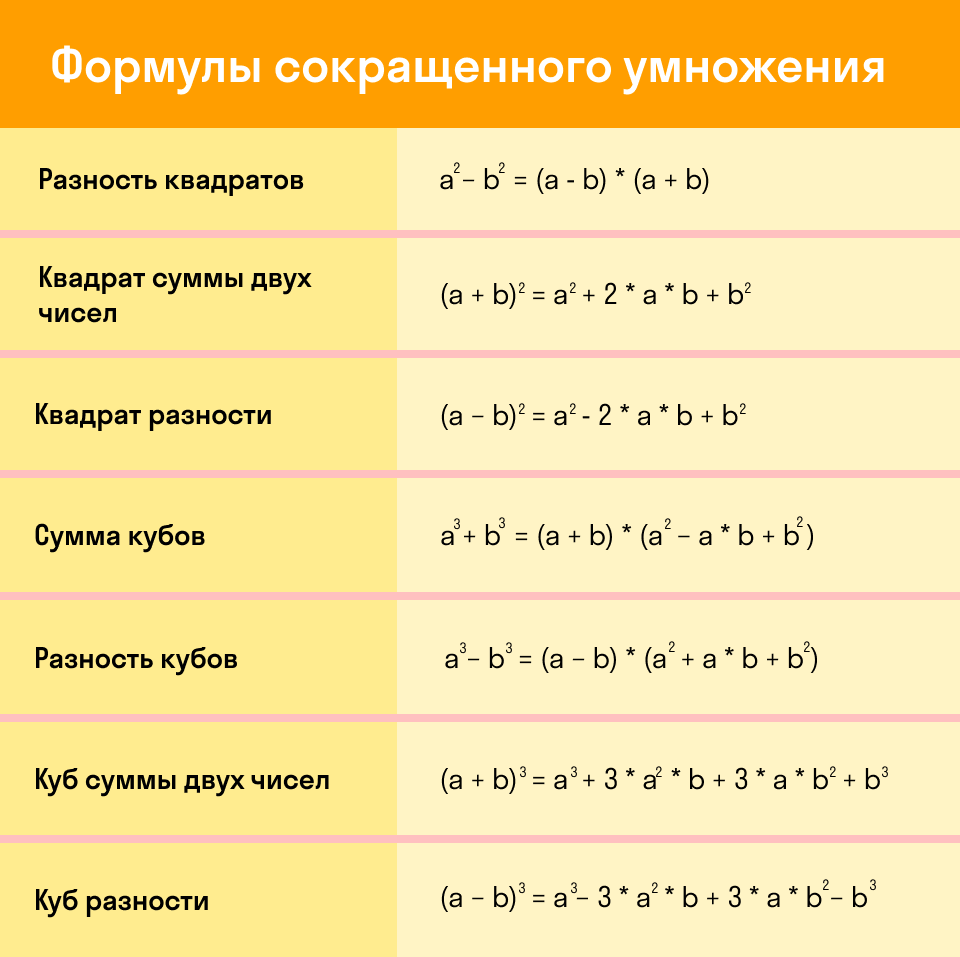
Формулы сокращенного умножения
Как читать формулы сокращенного умножения
Доказательство формул сокращенного умножения
Дополнительные формулы сокращенного умножения
Бином Ньютона
Формула возведения в квадрат суммы трех, четырех и более слагаемых
Формула разности n-ых степеней двух слагаемых
Решение задач
Задание 1
Задание 2
Задание 3
💥 Видео

Формула куба суммы

Возведем в куб сумму (a+b):

$$ = a(a^2+2ab+b^2 )+b(a^2+2ab+b^2 ) = a^3+2a^2 b+ab^2+a^2 b+2ab^2+b^3 = $$

Мы получили формулу куба суммы двух выражений:

Куб суммы двух выражений равен кубу первого выражения, плюс утроенное произведение квадрата первого выражения на второе выражение, плюс утроенное произведение первого выражения на квадрат второго выражения, плюс куб второго выражения.

Вместо a и b в формуле могут быть любые одночлены (и даже многочлены), которые нужно подставить. Например:

Формула куба разности

Возведем в куб разность (a-b):

$$ = a(a^2-2ab+b^2 )-b(a^2-2ab+b^2 ) = a^3-2a^2 b+ab^2-a^2 b+2ab^2-b^3 = $$

Мы получили формулу куба разности двух выражений:

Куб разности двух выражений равен кубу первого выражения, минус утроенное произведение квадрата первого выражения на второе выражение, плюс утроенное произведение первого выражения на квадрат второго выражения, минус куб второго выражения.

Вместо a и b в формуле могут быть любые одночлены (и даже многочлены), которые нужно подставить. Например:

Не забывайте о втором и третьем слагаемом в формулах куба двучленов!

Не путайте знаки «+» и «-» перед слагаемыми!

Примеры

Пример 1. Представьте в виде многочлена

а) $ (x+5)^3 = x^3+3cdot x^2cdot5+3cdot xcdot5^2+5^3 = x^3+15x^2+75x+125$

б) $ (9-z)^3 = 9^3-3cdot9^2cdot z+3cdot9cdot z^2-z^3 = 729-243+27z^2-z^3 $

в) $(5b-3c)^3 = (5b)^3-3cdot(5b)^2cdot3c+3cdot5bcdot(3c)^2-(3c)^3 =$

г) $(2mk+1)^3 = (2mk)^3+3cdot(2mk)^2cdot1+3cdot2mkcdot1^2+1^3 =$

$ = 8m^3 k^3+12m^2 k^2+6mk+1 $

Пример 2. Упростите выражение:

а) $(a+2)^3-(a-2)^3 = a^3+3a^2cdot2+3acdot2^2+2^3-(a^3-3a^2cdot2+3acdot2^2-2^3 )= $

б) $(x-3y)^3+9xy(x-3y) = x^3-3x^2cdot3y+3xcdot(3y)^2-27y^3+9x^2 y-27xy^2 =$

в) $(x+y)^3-x(x-y)^2 = x^3-3x^2 y+3xy^2+y^3-x(x^2-2xy+y^2 ) =$

$= x^3-3x^2 y+3xy^2+y^3-x^3+2x^2 y-xy^2 = -x^2 y+2xy^2+y^3$

г) $3m(k+3m)^2-(k+3m)^3 = 3m(k^2+6km+9m^2 )-$

$-(k^3+3k^2cdot3m+3kcdot(3m)^2+(3m)^3 ) = 3k^2 m+18km^2+27m^3- $

$-k^3-9k^2 m-27km^2-27m^3 = -6k^2 m-9km^2-k^3 $

Пример 3. Найдите значение выражения:

a) $a^3-b^3-3ab(a-b)$ при a = -7 и b = -17

$a^3-b^3-3ab(a-b) = a^3-b^3-3a^2 b+3ab^2 = a^3-3a^2 b+3ab^2-b^3 =$

Подставляем: $(-7-(-17) )^3 = 10^3 = 1000$

б) $3ab(a+b)+a^3+b^3$ при a = -3 и b = 13

$ 3ab(a+b)+a^3+b^3 = 3a^2 b+3ab^2+a^3+b^3 = a^3+3a^2 b+3ab^2+b^3 = $

Подставляем: $(-3+13)^3 = 10^3 = 1000$

Пример 4. Решите уравнение:

а) $(3x+1)^3 = 27x^2 (x+1)$

б) $(1-4x)^3+48x^2 (1 frac x-1) = 0$

$1-3cdot4x+3cdot(4x)^2-(4x)^3+48cdot frac x^3-48x^2 = 0 $

Пример 5*. Дайте геометрическое объяснение формуле куба суммы (аналогично квадрату суммы – см. §21 данного справочника, но для кубов в пространстве).

Рассмотрим куб со стороной (a+b) и вписанный в один из его углов куб со стороной b.

Объемы кубов $V_ = (a+b)^3,V_b = b^3$ Объем прямоугольного параллелепипеда, закрашенного оранжевым цветом: $V_ = a(a+b)^2$

Объем прямоугольного параллелепипеда, закрашенного синим: $V_ = b(a+b)^2$

Видео:Сумма и разность кубов двух выражений. 7 класс.Скачать

Алгебра. 7 класс

Конспект урока

Куб суммы. Куб разности

Перечень вопросов, рассматриваемых в теме:

Формулы сокращённого умножения.
Куб суммы. Куб разности.
Разложение многочлена на множители.
Тождественные преобразования.
Вычисление значения числовых выражений.

Формулы сокращённого умножения.

(a + b) 2 = a 2 + 2ab + b 2

(a – b) 2 = a 2 – 2ab + b 2

a 3 + b 3 = (a + b)(a 2 – ab + b 2 )

a 3 – b 3 = (a – b)(a 2 + ab + b 2 )

(a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3

(a – b) 3 = a 3 – 3a 2 b + 3ab 2 – b 3

упрощение умножения многочленов;
разложение многочлена на множители;
вычисление значения числового выражения;
тождественные преобразования.

1. Никольский С. М. Алгебра: 7 класс. // Никольский С. М., Потапов М. К., Решетников Н. Н., Шевкин А. В. – М.: Просвещение, 2017. – 287 с.

1. Чулков П. В. Алгебра: тематические тесты 7 класс. // Чулков П. В. – М.: Просвещение, 2014 – 95 с.

2. Потапов М. К. Алгебра: дидактические материалы 7 класс. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 96 с.

3. Потапов М. К. Рабочая тетрадь по алгебре 7 класс: к учебнику С. М. Никольского и др. «Алгебра: 7 класс». 1, 2 ч. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 160 с.

Теоретический материал для самостоятельного изучения.

(a + b) 3 = (a + b) 2 (a + b) = (a 2 + 2ab + b 2 )(a + b).

Применив правило умножения многочленов, и приведя подобные члены, получим:

a 3 + 2a 2 b + b 2 a + a 2 b + 2ab 2 + b 3 = a 3 + 3a 2 b + 3ab 2 + b 3 .

Итак, доказано равенство, которое называют «куб суммы»: (a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3

Читается так: «куб суммы двух чисел равен кубу первого числа, плюс утроенное произведение квадрата первого числа на второе, плюс утроенное произведение первого числа и квадрата второго, плюс куб второго числа».

Аналогично докажем формулу «куб разности».

(a – b) 3 = (a – b) 2 (a – b) =(a 2 – 2ab + b 2 )(a – b)

Применив правило умножения многочленов, получим:

a 3 – 2a 2 b + b 2 a – a 2 b + 2ab 2 – b 3 = a 3 – 3a 2 b + 3ab 2 – b 3

Доказано равенство, которое называют «куб разности»:

(a – b) 3 = a 3 – 3a 2 b + 3ab 2 – b 3

Читается так: «куб разности двух чисел равен кубу первого числа, минус утроенное произведение квадрата первого числа на второе, плюс утроенное произведение первого числа и квадрата второго, минус куб второго числа».

Формулы суммы и разности кубов часто используют для упрощения выражений.

Разбор решения заданий тренировочного модуля.

Найдите куб двучлена:

(a + 3) 3 = a 3 + 3a 2 · 3 + 3a · 3 2 + 3 3 = a 3 + 9a 2 + 27a + 27.

(10 – a) 3 =10 3 – 3 · 10 2 a + 3 · 10 · a 2 – a 3 = 1000 – 300a + 30a 2 – a 3 .

Упростите: x 3 + 3x(x + 4) – (x + 2) 3

x 3 + 3x 2 + 12x – (x 3 + 6x 2 + 12x + 8) =

Видео:Алгебра 7 класс (Урок№31 - Куб суммы. Куб разности.)Скачать

Сокращенное умножение: правила, формулы

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Видео:Куб суммы и куб разности двух выражений. 7 класс.Скачать

Формулы сокращенного умножения

Вместо букв a, b могут быть любые числа, переменные или даже целые выражения. Для быстрого решения задач лучше выучить основные 7 формул сокращенного умножения (ФСУ) наизусть. Да, алгебра такая, нужно быть готовым много запоминать.

Ниже удобная табличка, которую можно распечатать и использовать, как закладку для быстрого запоминания формул.

Видео:Куб суммы и куб разности двух выражений. Практическая часть. 7 класс.Скачать

Как читать формулы сокращенного умножения

Учимся проговаривать формулы сокращенного выражения:

Разность квадратов двух выражений равна произведению их разности и их суммы.
Квадрат суммы двух выражений равен квадрату первого плюс удвоенное произведение первого на второе плюс квадрат второго.
Квадрат разности двух выражений равен квадрату первого минус удвоенное произведение первого на второе плюс квадрат второго.
Сумма кубов двух выражений равна произведению суммы первого и второго на неполный квадрат их разности.
Разность кубов двух выражений равна произведению разности первого и второго на неполный квадрат их суммы.
Куб суммы двух выражений равен кубу первого плюс утроенное произведение квадрата первого на второе плюс утроенное произведение первого на квадрат второго плюс куб второго.
Куб разности двух выражений равен кубу первого минус утроенное произведение квадрата первого на второе плюс утроенное произведение первого на квадрат второго минус куб второго.

Обучение на курсах по математике — дорога к хорошим оценкам в школе и высокому баллу на экзамене.

Видео:Квадрат суммы и квадрат разности двух выражений. 7 класс.Скачать

Доказательство формул сокращенного умножения

Напомним, что разность квадратов двух чисел a и b равна произведению их разности и их суммы: a 2 — b 2 = (a — b) * (a + b).

Иначе говоря, произведение суммы a и b на их разность равна разности их квадратов: (a — b) * (a + b) = a 2 — b 2 .

Важно знать, что разность квадратов не равна квадрату разности: a 2 — b 2 ≠ (a — b) 2 .

Докажем, что a 2 — b 2 = (a — b) * (a + b).

a 2 — b 2 = a 2 — b 2 + ab — ab

Сгруппируем иначе: a 2 — b 2 + a * b — a * b = a 2 — a * b + a * b — b 2
Продолжим группировать: a 2 — a * b — b 2 +a * b = (a 2 — a * b) + (a * b — b 2 )
Вынесем общие множители за скобки:
(a 2 — a * b) + (a * b — b 2 ) = a *(a — b) + b *(a — b)

Вынесем за скобки (a — b). a * (a — b) + b * (a — b) = (a — b) * (a + b)
Результат доказательства: a 2 — b 2 = (a — b) * (a + b)
Для того, чтобы доказать в обратную сторону: (a — b) * (a + b) = a 2 — b 2 , нужно раскрыть скобки: (a — b) * (a + b) = a * a + a * b — b * a — b * b = a 2 — b 2 .

Остальные ФСУ можно доказать аналогичным методом.

Видео:Куб суммы и куб разностиСкачать

Дополнительные формулы сокращенного умножения

К таблице основных ФСУ следует добавить еще несколько важных тождеств, которые пригодятся для решения задач.

Бином Ньютона

Формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных. Записывается вот так:

Пример вычисления биномиальных коэффициентов, которые стоят в строке под номером n в треугольнике Паскаля:

ФСУ для квадрата и куба суммы и разности — являются частными случаями формулы бинома Ньютона при n = 2 и n = 3.

Формула возведения в квадрат суммы трех, четырех и более слагаемых

Пригодится, если слагаемых в сумме, которую нужно возвести в степень, больше, чем два.

Читается так: квадрат суммы n слагаемых равен сумме квадратов всех этих слагаемых и удвоенных произведений всех возможных пар этих слагаемых.

Формула разности n-ых степеней двух слагаемых

a n − b n = (a − b) * (a n-1 + a n-2 * b + a n-3 * b 2 + … + a * b n-2 + b n-1 ).

Для четных показателей можно записать так:

a 2*m − b 2*m = (a 2 − b 2 ) *(a 2*m−2 + a 2*m−4 * b 2 + a 2*m−6 * b 4 + … + b 2*m−2 ).

Для нечетных показателей:

a 2*m+1 − b 2*·m+1 = (a − b) * (a 2*m + a 2*m−1 * b + a 2*m−2 * b 2 + … + b 2*m ).

Частными случаями являются формулы разности квадратов и кубов при n = 2 и n = 3. Для разности кубов b можно также заменить на −b.

Видео:Куб суммы и куб разности двух выражений. Практическая часть. 7 класс.Скачать

Решение задач

Давайте потренируемся и рассмотрим примеры с дробями.

Задание 1

Что сделать: вычислить квадрат произведения (55 + 10) 2 .

Как решаем: воспользуемся формулой квадрата суммы: (55 + 10) 2 = 55 2 + 2 * 55 * 10 + 10 2 = 3025 + 1100 + 100 = 4225.

Задание 2

Что сделать: упростить выражение 64 * с 3 – 8.

Как решаем: применим разность кубов: 64 * с 3 – 8 = (4 * с) 3 – 2 3 = (4 * с – 2)((4 * с) 2 + 4 * с * 2 + 2 2 ) = (4 * с – 2)(16 * с 2 + 8 * с + 4).

Задание 3

Что сделать: раскрыть скобки (7 * y — x) * (7 * y + x).

Как решаем:

Произведем умножение: (7 * y — x) * (7 * y + x) = 7 * y * 7 * y + 7 * y * x — x * 7 * y — x * x = 49 * y 2 + 7 * y * x — 7 * y * x — x 2 = 49 * y 2 — x 2 .
Используем формулу сокращенного умножения: (7 * y — x) * (7 * y + x) = (7 * y) 2 — x 2 = 49 * y 2 — x 2 .

Многочленов бояться не стоит, просто совершайте последовательно каждое действие. С формулами решать задачки быстрее и удобнее — сохраняйте шпаргалку, запоминайте и радуйте своих учителей 🙂