Кто придумал уравнение и зачем

Видео:Откуда появляются дифференциальные уравнения и как их решатьСкачать

В мире уравнений

В мире уравнений

СОШ №41 с.Аксаково,

Кто и когда придумал первое уравнение? Ответить на этот вопрос, невозможно.

Теория уравнений интересовала и интересует математиков всех времен и народов. Задачи, сводящиеся к простейшим уравнениям, люди решали на основе здравого смысла с того времени, как они стали людьми. А учебные задачи, которые мы сегодня решаем при помощи уравнений, были хорошо известны еще в Древнем Вавилоне и Древнем Египте, Древнем Китае, Древней Индии и Древней Греции. Выделение алгебры в самостоятельную ветвь математики произошло в арабских странах, куда после распада Римской империи переместился центр научной деятельности. Там появился трактат «Китаб аль-джебр валь-мукабала», в котором были даны общие правила для решения уравнений первой и второй степени. Это сочинение оказало большое значение на развитие математики в Европе, а само слово «аль-джебр», входившее в название книги, постепенно стало названием науки -алгебра –области математики, связанной с искусством решения уравнений.

Выбор темы моего исследования не случаен, т.к. решение уравнений — едва ли не самый распространенный тип экзаменационных задач. На протяжении всех лет обучения в школе мы решаем уравнения, но школьный курс алгебры предусматривает ограниченный набор уравнений. Я умею, без ограничений, решать уравнения первой и второй степени, умею так же решать биквадратные уравнения и особого интереса к ним не проявляю. Интересны уравнения больших степеней. Поэтому объектом моего исследования стали уравнения высших степеней. Цель моей работы заключается в поиске методов решения уравнений произвольных степеней.

Под уравнениями высших степеней понимаются уравнения вида f(х)=0,где f(х)- многочлен степени выше двух. Это может быть кубическое уравнение aх 3 +bх 2 +cх+d=0 или уравнение четвертой степени aх 4 +bх 3 +cх 2 +dх+e=0, или уравнение пятой степени, и так далее. Среди них есть такие, решения которых сводятся, как правило, к квадратному уравнению, либо к определенным формулам Виета, Кардано, Феррари. Наиболее общий прием решения уравнений произвольной степени опирается на теорему Безу или ее следствия.

Таким образом, изучив научно-популярную литературу по данной теме, я выяснила, что корни любого уравнения не выше четвертой степени выражаются через коэффициенты уравнения формулой, в которой используются только четыре арифметические операции и извлечение корней степени, не превышающей степень уравнения. Более того, все уравнения не выше четвертой степени можно «обслужить» одной общей формулой. При подстановке в нее коэффициентов уравнения получим все корни. Общей формулы, применимой ко всем уравнениям пятой степени и выше, не существует. Но имеются специальные вычислительные методы, позволяющие найти корни любого уравнения с любой наперед заданной точностью, ничуть не меньшей, чем дают вычисления по готовым формулам, т.к. в прикладных задачах нас интересуют только приближенные значения корней уравнения, а его разрешимость в радикалах здесь обычно роли не играет.

Настоящая работа будет полезна любознательным школьникам, а так же может служить справочным учебным пособием для выпускников школы. Она позволит улучшить подготовку и математический кругозор в решении уравнений произвольных степеней.

Видео:Математика это не ИсламСкачать

Скачать:

Видео:Как решают уравнения в России и СШАСкачать

Предварительный просмотр:

Муниципальное бюджетное общеобразовательное учреждение

средняя общеобразовательная школа №41 с. Аксаково

муниципального района Белебеевский район РБ

В мире уравнений

МБОУ СОШ№41 с. Аксаково

Андреева Зинаида Маркеловна

1 Алгебра – наука о решении уравнений 5-6

2 Уравнения высших степеней

2.1 Кубические уравнения 7

2.2 Уравнения четвертой степени 8

2.3 Симметрические уравнения четвертой степени 9

2.4 Уравнения высоких степеней

2.5 Алгебраические уравнения и группы Галуа 10

3 Методы решения уравнений высших степеней

3.1 Разложение многочлена на множители 11

3.2 Метод введения параметра 12

3.3 Метод введения новой переменной

3.4 Комбинирование различных методов 13

3.5 Методы решения симметрических уравнений 3-й и 4-й степеней 14

3.6 Теорема Безу и ее следствия

3.7 Метод Кардано 16

3.8 Метод Феррари 17

3.9Теорема Виета 18-19

Приложение 22 2 Введение

1. Важность и актуальность исследования

Кто и когда придумал первое уравнение? Ответить на этот вопрос невозможно. Теория уравнений интересовала и интересует математиков всех времен и народов.

«Можно утверждать, что решение полиномиальных уравнений послужило исторически источником алгебры и что со времен вавилонян, индусов и Диофанта и до наших дней оно остается одной из основных целей» — эти слова французских математиков А. Гротендик (род. 1928) и Ж. Дьедоне (род. 1906), точки зрения которых придерживаются и современные ученые на содержание алгебры.

Выбор темы моего исследования тоже не случаен, так как решение уравнений — самый распространенный тип экзаменационных задач. На протяжении всех лет обучения в школе мы решаем уравнения, но школьный курс алгебры предусматривает ограниченный набор уравнений. Я умею, без ограничений, решать уравнения первой и второй степени и особого интереса к ним не проявляю. Интересны уравнения больших степеней.

Под термином «уравнения высших степеней» понимаются уравнения вида f(x)=0, где f(x)- многочлен степени выше двух. Это может быть кубическое уравнение aх 3 +вх 2 +cх+d=0 или уравнение четвертой степени ах 4 +bх 3 +сх 2 +dх+е=0, или уравнение пятой степени, и так далее. Среди них есть такие уравнения, решения которых сводятся, как правило, к линейным и квадратным по хорошо известным методам. Это разложение на множители многочлена f(х) и введение новой переменной. Но вызвал большой интерес нелинейные уравнения общего вида, решения которых невозможно найти указанными методами. Передо мной встал вопрос: существуют ли другие способы решения уравнений высших степеней? Не попытаться ли, как это делается в математике, отыскать общую формулу, пригодную для решения любых уравнений?

Материал исследования составляют теоретические и практические стороны решения уравнений высших степеней.

Объект исследования- уравнения высших степеней.

Предмет исследования — научно-популярная литература по математике.

3. Цель и задачи исследования

Цель исследования — найти методы решения уравнений высших степеней.

Общая цель исследования определяет конкретные задачи:

-изучить научно-популярную литературу по данной теме;

-выяснить существование специальных методов решения уравнений произвольной степени;

-установить, существует ли формула, выражающая корни любого алгебраического уравнения через конечное число алгебраических операций над его коэффициентами;

-на практике убедиться в правильности данных методов.

4. Практическая значимость исследования.

Материал данного исследования имеет практическую значимость и будет полезна любознательным школьникам, а так же выпускникам школы. Она позволит улучшить подготовку и расширить математический кругозор в решении уравнений произвольных степеней.

5. Методы исследования

Основными методами исследования являются:

1 Алгебра – наука о решении уравнений

Алгебра-часть математики, которая изучает общие свойства действий над различными величинами и решение уравнений, связанных с этими действиями. История алгебры уходит своими корнями в древние времена. Задачи, связанные с уравнениями решались еще в Древнем Египте и Вавилоне. Древние египтяне излагали свои алгебраические познания в числовой форме, не применяли буквенной символики. Путем проб и ошибок числа в условиях задач подбирались так, чтобы получались «хорошие» ответы (натуральные). Других чисел древние египтяне не знали. Более сложные задачи умели решать в Древнем Вавилоне. Там решались уравнения первой, второй и даже отдельные уравнения третьей степени. При этом вавилоняне так же не использовали букв, а излагали решения задач в словесной форме. Способы решения конкретных уравнений дают основание считать, что вавилоняне владели общими правилами нахождения корней уравнений первой и второй степени. Если при решении уравнения надо было извлекать квадратный корень из числа, не являющегося точным квадратом, находили приближенное значение корня. Но эти достижения еще нельзя было назвать наукой, т.к. не было общей теории.

Совсем другой вид приняла алгебра в Древней Греции. Все алгебраические утверждения выражали в геометрической форме. Древнегреческие математики работали не с числами, а с отрезками. Поэтому найти неизвестное для них означало построить отрезок. Большинство задач решалось путем построения циркулем и линейкой, но не все задачи поддавались такому решению. Ведь геометрически можно выразить лишь первые степени (длины), квадраты (площади) и кубы (объемы), но не высшие степени неизвестных. Геометрический путь решения уравнений был гениальной находкой античных математиков, но он сдерживал развитие алгебры. Алгебраические методы, ростки которых возникли в более ранних цивилизациях, в Древней Греции не получили развития.

Выделение алгебры в самостоятельную ветвь математики произошло в арабских странах, куда после распада Римской империи переместился центр научной деятельности. В Багдаде был создан «Дом мудрости», куда по воле халифа собрали образованных людей со всех сторон халифата. Эти мудрецы не только переводили труды своих великих предшественников, но и творили сами. Одним из них был Мухаммед бен Мусса аль- Хорезми. Наиболее значительным его трудом является трактат по алгебре, в котором впервые были разработаны правила преобразования уравнений. Уравнения у него, конечно, были с числовыми коэффициентами и выражались в словесной форме. Но на этих конкретных примерах он показывает способы решения основных типов линейных и квадратных уравнений. В греческих традициях строго геометрически обосновывает свои способы. Любое уравнение должно было быть преобразовано к одному из рассмотренных видов с помощью двух операций: 1) восполнение-перенесение отрицательных членов уравнения в другую часть; 2)противопоставление-приведение подобных членов. Это сочинение, которое по-арабски называется «Китаб аль-джебр вак-мукабала» оказало большое влияние на развитие математики в Европе, а само слово «аль-джебр», входившее в название книги, постепенно стало названием науки – алгебра ( области математики, связанной с искусством решения уравнений).

Итак, решать линейные и квадратные уравнения можно, не записывая каких-либо формул, не зная буквенных обозначений, а только лишь хорошо запомнив многочисленные правила. Но при решении уравнений третьей, четвертой и более высоких степеней без настоящей алгебры двигаться было трудно.

Для математиков, уже умевших — после вавилонян, Евклида и аль — Хорезми –решать линейные и квадратные уравнения, самым желанным было научиться решать уравнения третьей степени (кубические).

2 Уравнения высших степеней

2.1 Кубические уравнения

В 11 веке известный поэт, астроном и математик Омар Хайям без буквенной символики и отрицательных чисел описал все возможные виды уравнений третьей степени и рассмотрел геометрический способ их решения.. Занимался кубическими уравнениями и его современник арабский энциклопедист ал–Бируни. Корни уравнений третьей степени они строили при помощи пересечения парабол, гипербол, окружностей, каким способом решали задачи и греческие геометры. Но арабов, чья математика тяготела к вычислениям, интересовало и численное значение корней. Многие ученые пытались найти правило вычисления корней кубического уравнения, но потерпели неудачу.

Все кубические уравнения являются разновидностями уравнения самого общего вида, т.е. уравнения вида

аx 3 + bx 2 + cx + d =0, где а≠0

Со времен Омара Хайяма ученые средневековья почти 400 лет искали формулу для решения уравнения третьей степени. Были периоды, когда начинало казаться, что сил человеческого ума для решения этой задачи недостаточно. В конце ХV века профессор математики в университетах Рима и Милана Лука Пачоли в своём знаменитом учебнике «Сумма ‮знаний по арифметике, геометрии, отношениям и пропорциональности» задачу о нахождении общего метода решения кубических уравнений ставил в один ряд с задачей о квадратуре круга. И все же усилиями итальянских алгебраистов Даля Ферро, Никколо Тартальей, Джероламо Кардано вскоре такой метод был найден- выделение полного куба. Д.Кардано написал большую книгу, посвященную алгебре. Главным украшением этой книги и была «формула Кардано», как ее называют теперь. Но формулу Кардано нельзя применять без учета некоторых дополнительных условий и ограничений. Пусть практическое значение этих формул невелико-трудно переоценить тот мощный импульс, который они дали развитию современной алгебры.

Важный вклад в развитии науки внес французский математик Франсуа Виет. Пытаясь решить задачу, каким образом корни уравнения выражаются через коэффициенты, он записал систему равенств. Отыскивая одно, он придумал другое: обозначить буквами не только неизвестные, но и коэффициенты при них. Путем преобразований Ф.Виет доказал, что второй коэффициент данного уравнения приведенного вида равен сумме корней уравнения, взятой с противоположным знаком, третий коэффициент равен сумме попарных произведений корней уравнения, четвертый коэффициент равен сумме всех возможных произведений корней уравнения по три, взятой с противоположным знаком и т.д., свободный член уравнения равен произведению всех корней уравнения, умноженному на (-1) n . Эта связь коэффициентов уравнения приведенного вида с его корнями называется обобщенной теоремой Виета. Она позволяет более легко составлять уравнения по их корням. Хотя буквенная символика Виета обладала некоторыми недостатками, тем не менее это был огромный шаг вперед, до него в математике не было формул. Недаром Виета часто называют «отцом алгебры».

2.2 Уравнения четвертой степени

Метод решения уравнений четвертой степени нашел в ХVI в. Лудовико Феррари, ученик Джероламо Кардано. Он так и называется — метод Феррари.

Как и при решении кубического и квадратного уравнений, в уравнении четвертой степени

x 4 +px 3 +qx 2 +rx+s=0

можно избавиться от члена px 3 подстановкой x=y-p/4. Поэтому будем считать, что коэффициент при кубе неизвестного равен нулю:

Идея Феррари состояла в том, чтобы представить уравнение в виде А 2 =В 2 , где левая часть- квадрат выражения А=x 2 +s, а правая часть- квадрат линейного выражения В от х, коэффициенты которого зависят от s. После этого останется решить два квадратных уравнения: А=В и А=-В. Конечно, такое представление возможно только при специальном выборе параметра s.

2.3 Симметрические уравнения четвертой степени

Если уравнение имеет вид Р(Q(x))=0, где Р и Q- многочлены, то замена y=Q(x) сводит его решение к решению двух уравнений меньших степеней: Р(y)=0 и Q(x)=y. Замена используется, в частности, при решении биквадратных уравнений.

Более интересный случай- возвратные уравнения, т.е. уравнения четвертой степени

a 2n x 2n +a 2n-1 x 2n-1 +…+a 1 x+a 0 =0,

в которых коэффициенты, одинаково отстоящие от концов, равны: a 2n = a 0, a 2n-1= a 1 и т.д. Такое уравнение сводится к уравнению вдвое меньшей степени делением на x n и последующей заменой y=x±1/x.

При решении возвратных уравнений более высоких степеней обычно используют тот факт, что выражение x k +1/x k при любом k можно представить как многочлен степени k от y=x+1/x.

2.4 Уравнения высоких степеней

Формула корней квадратного уравнения известна с незапамятных времен, а в XVI в. итальянские алгебраисты решили в радикалах уравнения третьей и четвертой степеней. Таким образом, было установлено, что корни любого уравнения не выше четвертой степени выражаются через коэффициенты уравнения формулой, в которой используются только четыре арифметические операции (сложение, вычитание, умножение, деление) и извлечение корней степени не превышающей степень уравнения. Более того все уравнения данной степени n(n≤4) можно «обслужить» одной общей формулой. При подстановке в нее коэффициентов уравнения получили все корни — и действительные, и комплексные.

После этого естественно возник вопрос: а есть ли похожие общие формулы для решения уравнений пятой степени и выше? Ответ на него смог найти норвежский математик Нильс Хенрик Абель вначале XIX в. Чуть раньше этот результат был указан, но недостаточно обоснован итальянцем Паоло Руффини. Теорема Абеля — Руффини звучит так:

Общее уравнение степени n при n≥5 неразрешимо в радикалах.

Таким образом, общей формулы, применимой ко всем уравнениям данной степени n≥5, не существует.

Хотя уравнения высоких степеней неразрешимо в радикалах, да и формулы Кардано и Феррари для уравнений третьей и четвертой степеней в школе не проходят, в учебниках по алгебре, на вступительных экзаменах в институты иногда встречаются задачи, где требуется решить уравнение выше второй степени. Обычно их специально подбирают так, чтобы корни уравнений можно было найти с помощью некоторых элементарных приемов.

2.5 Алгебраические уравнения и группы Галуа

Теория Галуа позволяет выяснить для любого конкретного уравнения, решается ли оно в радикалах. Для этого данному уравнению сопоставляется некоторая группа перестановок его корней. Важно, что эту группу, названную сейчас группой Галуа, можно определить, не вычисляя корней уравнения, только по его коэффициентам. Галуа установил связь между разрешимостью алгебраического уравнения в радикалах и особым свойством группы этого уравнения, которое также было названо разрешимостью. В частности, любая коммутативная группа разрешима. Если коэффициенты уравнения рациональны и его левая часть не разлагается на множители с рациональными коэффициентами (неприводима), то это уравнение разрешимо в радикалах только тогда, когда разрешима его группа Галуа.

Например, уравнение x 5 — 4x + 2=0 имеет пять различных корней. Хотя они нам неизвестны, можно показать, что группа Галуа данного уравнения совпадает с группой всех перестановок его пяти корней — это самая «большая» из возможных групп для уравнений пятой степени. Доказывается, что эта группа неразрешима. Следовательно, корни данного уравнения не выражаются в радикалах, а значит, общей формулы для решения уравнений пятой степени в радикалах не существует.

3 Методы решения уравнений высших степеней

3.1 Разложение многочлена на множители

При решении алгебраических уравнений часто приходится разлагать многочлен на множители. Разложить многочлен на множители — это значит представить его в виде произведения двух или нескольких многочленов. Некоторые методы разложения многочленов мы употребляем достаточно часто: вынесение общего множителя, применение формул сокращенного умножения, выделение полного квадрата, группировка. Рассмотрим ещё некоторые методы.

Иногда при разложении многочлена на множители бывают полезными следующие утверждения:

1. если многочлен a n +a n-1 x+…+a 0 x n ,a 0 ≠0, с целыми коэффициентами имеет рациональный корень х= p/q (где p/q- несократимая дробь, p є Z, q є N), то p- делитель свободного члена a n , а q- делитель старшего коэффициента а 0 ;
2. если каким-либо образом подобрать корень х=а многочлена Р n (x) степени n, то многочлен Р n (x) можно представить в виде Р n (х)=(х-а) Р n-1 (х), где Р n-1 (х)- многочлен степени n-1.

Многочлен Р n-1 (х) можно найти либо делением многочлена Р n (х) на двучлен (х-а) «столбиком», либо соответствующей группировку слагаемых многочлена и выделением из них множителя х-а, либо методом неопределенных коэффициентов.

Пример. Разложить на множители многочлен

х 4 -5х 3 +7х 2 -5х+6

Решение. Поскольку коэффициент при х 4 равен 1, то рациональные корни данного многочлена, существуют, являются делителями числа 6, т.е. могут быть целыми числами ±1, ±2, ±3, ±6. Обозначим данный многочлен через Р 4 (х). Так как Р 4 (1)=4 и Р 4 (-4)=23, то числа 1 и -1 не являются корнями многочлена Р А (х). Поскольку Р 4 (2)=0, то х=2 является корнем многочлена Р 4 (х), и, значит, данный многочлен делится на двучлен х-2.

х 4 -5х 3 +7х 2 -5х+6 х-2

х 4 -2х 3 х -3х +х-3

-3х +7х -5х+6

-3х +6х

х -5х+6

х -2х

-3х+6

Следовательно, Р 4 (х)= (х-2)( х -3х +х-3). Так как х -3х +х-3 =

= х 2 (х-3)+(х-3)= (х-3)(х 2 +1), то х 4 -5х 3 +7х 2 -5х+6=(х-2)(х-3)(х 2 +1).

3.2 Метод введения параметра

Иногда при разложении многочлена на множители помогает метод введения параметра. Суть этого метода можно пояснить на следующем примере.

Пример. х 3 -(√3+1)х 2 +3.

Решение : рассмотрим многочлен с параметром а:

который при а=√3 превращается в заданный многочлен. Запишем этот многочлен как квадратный трехчлен относительно а:

а 3 -ах 2 +(х 3 -х 2 ).

Так как корни этого квадратного относительно а трехчлена есть а 1 =х и а 2 =х 2 -х, то справедливо равенство а 2 -ах 2 +(х 3 -х 2 ) = (а-х)(а-х 2 +х). Следовательно, многочлен х 3 -(√3+1)х 2 +3 разлагается на множители √3-х и √3-х 2 +х, т.е.

х 3 -(√3+1)х 2 +3=(√3-х)( х 2 -х-√3).

3.3 Метод введения новой переменной

В некоторых случаях путем замены выражения f(х), входящего в многочлен через у можно получить многочлен относительно у, который уже легко разложить на множители. Затем после замены у на f(х) получаем разложение на множители многочлена Р n (х).

Пример: разложить на множители многочлен

Решение : преобразуем данный многочлен следующим образом:

(х+1)(х+2)(х+3)-15= = (х 2 +3х)( х 2 +3х+2)-15.

Обозначим х 2 +3х через у. тогда имеем

х(х+1)(х+2)(х+3)-15=( х 2 +3х+5)( х 2 +3х-3).

Пример: разложить на множители многочлен (х-4) 4 +(х+2) 4

Решение : обозначим = х-1 через у.

Тогда (х-4) 4 +(х+2) 4 =(у-3) 4 +(у+3) 4 =у 4 -12у 3 +54у 3 -108у+81+у 4 +12у 3 +54у 3 +108у+81=

=2у 4 +108у 2 +162=2(у 4 +54у 2 +81)=2((у 2 +27) 2 -648)=2(у 2 +27-√648)(у 2 +27+√684)=

=2((х-1) 2 +27-√684)((х-1) 2 +27+√684)=2(х 2 -2х+28-18√2)( х 2 -2х+28+18√2).

3.4 Комбинирование различных методов

Часто при разложении многочлена на множители приходится применять последовательно несколько из рассмотренных выше методов.

Пример: разложить на множители многочлен

Решение : Применяя группировку, перепишем многочлен в виде

х 4 -3х 2 +4х-3=( х 4 -2х 2 )-(х 2 -4х+3).

Применяя к первой скобке метод выделения полного квадрата, имеем:

х 4 -3х 2 +4х-3=(х 4 -2∙1∙х 2 +1)(х 2 -4х+4).

Применяя формулу полного квадрата, можно теперь записать, что:

х 4 -3х 2 +4х-3=(х 2 -1) 2 -(х-2) 2 .

Наконец, применяя формулу разности квадратов, получим, что:

х 4 -3х 2 +4х-3=( х 2 -1+х-2)( х 2 -1-х+2)=( х 2 +х-3)(х 2 -х+1).

3.5 Решение симметрических уравнений третьей и четвертой степеней

а) решение симметрических уравнений третьей степени.

Пример: решить уравнение 3х 3 +4х 2 +4х+3=0.

Решение : это уравнение является симметрическим уравнением третьей степени.

Поскольку 3х 3 +4х 2 +4х+3=3(х 3 +1)+4х(х+1)=(х+1)(3х 2 -3х+3+4х)=

=(х+1)(3х 2 +х+3), то данное уравнение равносильно совокупности уравнений

Решение первого из этих уравнений есть х= -1, второе уравнение решений не имеет.

б) решение симметрических уравнений четвертой степени.

Пример: решить уравнение х 4 -5х 3 +8х 2 -5х+1=0.

Решение : Данное уравнение является симметрическим уравнением четвертой степени. Так как х=0 не является его корнем, то, разделив данное уравнение на х 2 , получим равносильное ему уравнение:

х 2 -5х+8-5/х+1/х 2 =0

Сгруппировав слагаемые, перепишем уравнение в виде

х 2 +1/х 2 -5(х+1/х)+8=0

Заменив х+1/х на у, получим уравнение

имеющее два корня у 1 =2 и у 2 =3. Следовательно, исходное уравнение равносильно совокупности уравнений х+1/х=2 и х+1/х=3.

Решение первого уравнения этой совокупности есть х =1, а решение второго есть х и х 3 = .

Следовательно, исходное уравнение имеет три корня: х , х , х 3.

3. 6 Теорема Безу и ее следствия.

Наиболее общий прием решения уравнений высших степеней опирается на теорему Безу и ее следствия. Рассмотрим эту теорему и её следствия.

Пусть имеем многочлен М(х)=а 0 х n +а 1 х n-1 +…+a n , целый относительно х, т.е. многочлен с целыми неотрицательными показателями х, х-а- двучлен. Тогда теорема Безу утверждает:

Остаток от деления многочлена, целого относительно х, на двучлен х-а равен значению многочлена при х=а.

Если разделить многочлен М(х) на х-а, то в частности получится многочлен Q(x), степень которого на 1 меньше степени многочлена М(х), и некоторый остаток R. Очевидно, что остаток R не содержит х, т.е равен постоянному числу, так как степень остатка меньше степени делителя.

Тогда М(х)=(х-а)Q(х)+R. Это равенство верно при любом значении х. Оно является тождеством. Положим в нем х=а. Получим:

т.е М(а)=R, R= М(а). Теорема доказана.

Значение а, при котором R=0, называется корнем многочлена М(х). Оно является и корнем уравнения М(х)=0, так как М(а)=0.

Основная теорема алгебры утверждает, что любой многочлен с числовыми коэффициентами, целый относительно х, имеет по крайней мере один корень х 1 . Из теоремы Безу в этом случае следует, что М(х)=(х- х 1 ) Q(x),где степень многочлена Q(x) на 1 меньше степени многочлена М(х). Заменим в уравнении М(х)=0 левую часть произведения (х- х 1 ) Q(x). Получим (х- х 1 ) Q(x)=0. Приравнивая к нулю множитель х- х 1 , получим уже найденный корень х 1 . Приравняем к нулю второй множитель Q(x)=0. Рассуждая аналогично предыдущему, получим, что последнее уравнение имеет хоть один корень х 2 . Тогда левую часть уравнения Q(x)=0 можно заменить произведением (х-х 2 )Q 1 (х)=0, где Q 1 (х)-многочлен степени n-2. Продолжая рассуждать дальше, убеждаемся, что уравнение n-й степени имеет ровно n действительных или мнимых корней.

Если все коэффициенты в уравнении — действительные числа, то каждый мнимый корень уравнения обязательно имеет сопряженный ему корень этого уравнения, т.е. если уравнение с действительными коэффициентами имеет корень х 1 =а+bi, то оно имеет и корень х 2 =а-bi.

Пример: решить уравнение х 4 -3х 3 -8х 2 +12х+16=0.

Решение : выписываем делители свободного члена 16:

При х=1 в левой части уравнения получим 1-3-8+12+16≠0. Единица не является корнем уравнения.

Проверим х=-1. Левая часть уравнения будет равна 1+3-8-12+16=0, х 1 = -1-корень уравнения.

Делим левую часть уравнения на х-х 1 =х+1:

х 4 -3х 3 -8х 2 +12х+16 х+1

± х 4 ± х 3 х 3 -4х 2 -4х+16

±4 х 3 ±4х 2

±4х 2 ±4х

16х+16

Приравниваем к нулю полученное частное:

Проверяем, является ли х=2 корнем этого уравнения:

8-16-8+16=0, т.е. х 2 =2 – корень этого уравнения.

3.7 Метод Кордано

Данным методом решаются лишь уравнения вида х 3 + рх + q = 0

Используем формулу куба суммы: (a + b) 3 = a 3 + 3a 2 b + b 3 = a 3 + b 3 + 3ab·(a + b)

Заменим (а + b) на х:

х 3 – 3abx – (a 3 – b 3 ) = 0

Исходное уравнение равносильно системе уравнений:

Эту систему можно решать по-разному, но результат один:

Это и есть формула Кардано , часто использующаяся при решении кубических уравнений, когда обычные методы не помогают.

Пример. Решим уравнение х 3 + 15х + 124 = 0

Решение. Имеем p = 15, q = 124.

3.8 Метод Феррари

х 4 + dx 3 + ax 2 + bx + c = 0

Избавляемся от dx 3 подстановкой

х 4 + ах 2 + bx + с = 0.

Идея в том, чтобы представить уравнение в виде А 2 =В 2 , где А = х 2 + s, а В – линейная функция от х. Тогда останется решить уравнение А = ± В.

Возьмем Тогда, учитывая исходное равенство, получим:

Пусть t 0 – корень последнего уравнения. Тогда при t = t 0 правая часть-квадрат:

Решив эту систему, мы найдем решение исходного уравнения.

Это и есть метод Феррари.

Пример. х 4 + 8х 3 + 11 = 68х

Решение . Добавив к обеим частям уравнения 16х 2 и перенеся свободный член вправо, перепишем уравнение следующим образом:

(х 2 +4х) 2 =16х 2 +68х-11

Введем неизвестное t и добавим к обеим частям уравнения выражение t 2 -2(х 2 +4х)t.

( х 2 + 4х – t) 2 = ( 16 — 2t)х + ( 68 — 8t)х — ( 11 – t 2 ).

Левая часть уравнения является квадратом. Найдем такое значение t, при котором квадратный трехчлен от х, стоящий в правой части, тоже является полным квадратом. Для этого нужно, чтобы дискриминант квадратного трехчлена равнялся нулю, т.е. чтобы выполнялось равенство

( 34 — 4t) 2 + (16 — 2t) (1 1 – t 2 ) = 0.

Раскрыв в нем скобки, придем к кубическому уравнению

t 3 – 147t + 666 = 0, где t = 6 –корень уравнения.

При t = 6 исходное уравнение принимает вид:

( х 2 + 4х – 6 ) 2 = ( 2х + 5 ) 2 .

Значит, х 2 + 4х – 6 = ±(2х + 5).

Решая оба получившихся уравнения, найдем четыре корня данного уравнения:

3.9 Теорема Виета

х 3 + px 2 + qx + r = 0

Если х 1 , х 2 , х 3 – корни уравнения, то его можно записать в виде

(х – х 1 )·(х – х 2 )·(х – х 3 ) = 0

Преобразуем, раскрыв скобки:

х 3 – (х 1 + х 2 + х 3 )х 2 + (х 1 х 2 + х 1 х 3 + х 2 х 3 )х – х 1 х 2 х 3 = 0

Имеем возможность вместо одного уравнения третьей степени записать такую систему из трех уравнений:

Видео:Как мнимые числа спасли математику [Veritasium]Скачать

Эти загадочные уравнения

Окружная научная конференция учащихся

Эти загадочные уравнения

Наумов Виктор, ученик 6 класса

ГБОУ СОШ ж.-д. ст. Погрузная

ГБОУ СОШ ж.-д. ст. Погрузная

с. Красный Яр, 2013 г.

· Введение. Актуальность проблемы изучения способов решения

Глава 1. Исторические сведения…………………………………….4-8

Глава 2. Эти загадочные уравнения………………………………..8-15

2.1. Что мне было известно про уравнение………………………..8-9

2.2. Решение простейших уравнений …………………..……

2.3. Что я нового узнал об уравнениях из школьных учебников……………………………………………………………11-15

Глава 3. Что я нового узнал об уравнении из дополнительной

3.1. Тайное становится явным (исследование)………….……… 15-18

3.2. Способы решения уравнений……………………….……….. 18-20

а) Решение уравнений с помощью правила нахождения неизвестной компоненты…………………………………………………….…………..18

б) Решение уравнений методом весов…………………………..18

в) Решение уравнений методом проб и ошибок………………..19

г) Решением уравнений методом перебора……………. 19

3.3 Математические фокусы…………………………………. 21-23

· Список использованной литературы……………………. 25

· Приложения. Задания для моих одноклассников

Введение. Актуальность проблемы

Уравнение – одно из важнейших понятий математики. В большинстве практических и научных задач, где какую-то величину нельзя непосредственно измерить или вычислить по готовой формуле, удается составить выражение, которым оно удовлетворяет. Так получают уравнение для определения неизвестной величины. Кто и когда придумал уравнения? Кто ввёл неизвестные величины? Как решаются уравнения? Эти проблемные вопросы, думаю, интересны многим, в том числе и мне. Я высказал гипотезу, что существуют какие-то определенные способы решения уравнений и поставил перед собой цель:

• изучить способы решения уравнений

• углубить математические знания по этой теме

• расширить представления о математике как о языке описания окружающего мира

• изучить литературу и систематизировать материал по данной теме

• исследовать свойства преобразования уравнений

• выявить основные доступные способы решения уравнений

• выработать навыки поисково-исследовательской работы

• систематизация изученного материала

• классификация уравнений по способам их решения

Объект исследования: Уравнения

Предмет исследования: Способы решения уравнений

Слова уравнение и равенство имеют один и тот же корень. Да, и на самом деле, уравнение – это равенство, содержащее неизвестную величину, значение которой нужно найти.

Уравнения в школьном курсе математики занимают ведущее место. На их изучение отводится времени больше, чем на любую другую тему. Подавляющее большинство задач о пространственных формах и количественных отношениях реального мира сводится к решению различных видов уравнений. Овладевая способами их решения, мы находим ответы на различные вопросы из науки и техники.

В начальной школе я научился решать самые простые уравнения, в пятом и шестом классах мы уже решали более сложные уравнения, а в старших классах я научусь решать разные виды уравнений. Существует целая наука алгебра, которая изучает различные виды уравнений и способы их решения. С алгеброй, как учебным предметом, мне предстоит встретиться только в седьмом классе.

Но мне не захотелось ждать седьмого класса. Из дополнительной литературы я решил узнать новое, интересное и загадочное об уравнениях. Поэтому тема моей работы «Эти загадочные уравнения».

Глава 1.Исторические сведения

Кто и когда придумал первое уравнение?

Задачи, которые довольно просто мы сегодня можем решить при помощи уравнений, решали хорошо обученные науке мудрецы, чиновники и жрецы ещё в Древнем Вавилоне и Древнем Египте, Древнем Китае, Древней Индии и Древней Греции. Дошедшие до нас источники свидетельствуют, что древние учёные владели какими-то общими приёмами решения задач с неизвестными. Однако ни в одном папирусе, ни на одной глиняной табличке не дано описание приёмов. Авторы лишь изредка снабжают выкладки скупыми комментариями типа: «Смотри!», «Делай так!», «Ты верно нашёл!» В те времена не было ещё общепринятых теперь обозначений неизвестных буквами, а действий – знаками. Древние египтяне для удобства рассуждений придумали специальное слово, обозначающее неизвестное число, но так как у них не было ещё знаков равенства и знаков действий, то записывать уравнения они, конечно, не умели. Уравнения записывались словами.

Но и в «словесной форме» уравнения существенно облегчали решение задач.

Первым придумал обозначение для

неизвестных греческий математик

Диофант, живший в III веке.

Посредством уравнений, теорем

Он уйму всяких разрешал проблем.

И засуху предсказывал, и ливни –

Поистине его познанья дивны.

Его книга «Арифметика» содержала большое количество интересных задач, её изучали математики всех поколений. Книга сохранилась до наших дней и переведена на русский язык.

Во времена Диофанта языком науки был греческий. Но греки ещё не знали цифр и обозначали числа при помощи букв своего алфавита. Первые девять букв: обозначали числа от 1 до 9; следующие девять:обозначали числа от 10 до 90; наконец, следующие девять: обозначали числа от 100 до 900. чтобы не ошибиться и не принять число за слово, над буквами, обозначающими число, ставилась чёрточка. Букв в алфавите было 28, одна из них была особой – она обозначалась (сигма концевая), ставилась только в конце слов и числового значения не имела. Вот ею-то Диофант и стал обозначать неизвестную величину, так же как мы обычно обозначаем её буквой х.

Придумав это, Диофант стал двигаться дальше. И вместо слова «получится» или «равняется» стал писать — две первые буквы слова («исос» — равный). Диофант придумал знак и для вычитания – им служила буква (пси), только перевёрнутая. А без знака сложения Диофант обходился довольно просто – слагаемые записывал рядом друг с другом. Придумал Диофант и два основных приёма решения уравнений – перенос неизвестных в одну сторону уравнения и приведение подобных членов. С этими приёмами я познакомлюсь при изучении математики в этом году.

Первым руководством по решению уравнений, получившим широкую известность, стал труд арабского учёного IX века Мухаммеда Бен Мус аль -Хорезми. Об аль – Хорезми известно лишь, что он написал ряд трудов по астрономии и географии. И самое главное – он написал сочинение, которое по-арабски называется «Китаб аль-джебр валь-мукабала» (Книга о восстановлении и противопоставлении). Это сочинение оказало большое влияние на развитие математики в Европе, а само слово «аль-джебр», входившее в название книги, постепенно стало названием науки – алгебра. Алгебра – часть математики, которая изучает общие свойства действий над различными величинами и решение уравнений, связанных с этими действиями.

Аль-Хорезми одним из первых стал обращаться с уравнениями так, как торговец обращается с рычажными весами. Пусть, например, имеется равенство 5х – 16 = 20 – 4х. Считая, что оно задаёт равновесие некоторых грузов на чашах весов, торговец вправе заключить, что равенство не изменится, если он на обе чаши добавит одно и то же количество:

было 5х – 16 = 20 – 4х,

стало 5х = 36 – 4х.

После этой операции прибавления одинаковых количеств число 16 исчезло из левой части исходного равенства, зато со знаком плюс оно возникло (восстановилось) в правой части. Точно так же на обе чаши весов можно добавить одно и то же количество 4х:

было 5х = 36 – 4х.,

Опять из правой части равенства выражение 4х пропало, а в левой части оно восстановилось со знаком плюс. Из полученного простого равенства 9х = 36 уже легко вычислить, что х = 4.

Взгляд на уравнение как на равенство грузов на весах, на обеих чашах которых можно производить одинаковые преобразования, оказался очень плодотворным. Равные количества можно не только прибавлять к обеим частям уравнения или вычитать из них. Равенство не нарушится и тогда, когда обе части умножаются или делятся на одно и то же число (если оно не нуль). Главный принцип: если над равными количествами произвести одинаковые действия, то в результате снова получатся равные количества – стал своеобразной «волшебной палочкой», которую обнаружили вдумчивые читатели руководства аль-Хорезми.

Новый великий прорыв в решении уравнений связан с именем французского учёного XVI века Франсуа Виета. Он первым из математиков ввёл буквенные обозначения для неизвестных величин. А традицией обозначать неизвестные величины последними буквами латинского алфавита (х, у или z) мы обязаны соотечественнику Виета – Рене Декарту.

Таким образом, решению уравнений уделялось всегда большое внимание. В древности считалось, что уравнения связаны с тайной, которую нужно разгадать, найдя значение неизвестной величины. Людей, которые могли решать уравнения, считали мудрецами, посвященными в эту тайну, так как уравнения были связаны с решением житейских проблем.

Уравнение – это золотой ключ, открывающий все математические сезамы» С. Коваль

Сезам – заклинание в арабской сказке, силой которого раскрывалась тайная сокровищница.

Глава 2. Эти загадочные уравнения.

2.1.Что мне было известно про уравнение

В учебнике «Математика – 4, часть 2» в разделе «Справочный материал» на странице 92 про уравнение можно прочитать следующее:

« Уравнение – это равенство, содержащее неизвестное число, которое надо найти. Неизвестное число в таком равенстве обозначают латинской буквой (например, х, а, b и др.). Решить уравнение – значит найти такое значение буквы, чтобы равенство стало верным. Например: 15 + х = 18 – уравнение. х = 3 – решение уравнения, так как 15 + 3 = 18 – верное равенство».

В учебнике Виленкина «Математика – 5», в п.10 на страницах 58-59 мы прочтём про уравнение почти то же самое.

Задача. На левой чашке весов лежит арбуз и гиря в 2 кг, а на правой чашке – гиря в5 кг. Весы находятся в равновесии. Чему равна масса арбуза?

Решение. Обозначим неизвестную массу арбуза буквой х. Так как весы находятся в равновесии, то должно выполняться равенство х + 2 = 5.

Нужно найти такое значение х, при котором выполняется это равенство. По смыслу вычитания таким значением будет разность чисел 5 и 2, то есть 3. Значит, масса арбуза равна 3 кг. Пишут: х = 3.

Если в равенство входит буква, то равенство может быть верным при одних значениях этой буквы и неверным при других её значениях.

Например, равенство х + 2 = 5 верно при х = 3 и неверно при х = 4.

Уравнением называют равенство, содержащее букву, значение которой надо найти. Значение буквы, при котором из уравнения получается верное числовое равенство, называют корнем уравнения. (Например, корнем первого уравнения х + 2 = 5 является число3).

Решить уравнение – значит найти все его корни (или убедиться, что это уравнение не имеет ни одного корня).

Таким образом, уравнение характеризуется двумя свойствами, которые легко определить на глаз, по внешнему виду: 1) уравнение – это равенство; 2) в этом равенстве есть буква.

2.2. Решение простейших уравнений

Пример 1. Решим уравнение х + 37 = 85.

Решение. По смыслу вычитания неизвестное слагаемое равно разности суммы и другого слагаемого. Поэтому х = 85 – 37 , то есть х = 48.Число 48 является корнем уравнения х + 37 = 85, потому что 48 + 37 = 85.

Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое.

Пример 2. Решим уравнение у – 94 = 18.

Решение. По смыслу вычитания у является суммой чисел 18 и 94. Значит, у = 18 + 94, то есть у = 112.Число 112 является корнем уравнения у – 94 = 18, так как верно равенство у – 94 = 18.

Чтобы найти неизвестное уменьшаемое, надо сложить вычитаемое и разность.

Пример 3. Решим уравнение 91 – z = 36.

Решение. По смыслу вычитания число 91 является суммой z и 36 , то есть z + 36 = 91. Из этого уравнения находим неизвестное слагаемое: z = 91 – 36, то есть z = 55.Число 55 является корнем уравнения 91 – z = 36, так как верно равенство 91 – 55 = 36.

Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.

Пример 4. Решим уравнение 35х = 175.

Решение. По смыслу деления имеем: х = 175 : 35, то есть х = 5. Число 5 является корнем уравнения 35х = 175, так как верно равенство 355 = 175.

Чтобы найти неизвестный множитель, надо произведение разделить на другой множитель.

Пример 5. Решим уравнение у : 8 = 16.

Решение. По смыслу деления у – произведение множителей 8 и 16. Значит, у = 168, то есть у = 128. Число 128 является корнем уравнения у : 8 = 16, так как верно равенство 128 : 8 = 16.

Чтобы найти неизвестное делимое, надо частное умножить на делитель.

Пример 6. Решим уравнение 252 : z = 21.

Решение. По смыслу деления число 252 – произведение множителей 21 и z, то есть 21z = 252. Применяя правило нахождения неизвестного множителя, находим: z = 252 : 21, то есть z = 12. Число 12 является корнем уравнения 252 : z = 21, так как верно равенство 252 : 12 = 21.

Чтобы найти неизвестный делитель, надо делимое разделить на частное.

Таким образом, при решении этих уравнений я использовал правила нахождения неизвестных компонентов арифметических действий (слагаемого, уменьшаемого, вычитаемого, множителя, делимого и делителя).

Компонент — слово латинского происхождения, на русский язык переводится как составляющая часть, элемент чего-либо. По этим правилам мы решаем уравнения, начиная со второго класса.

2.3.Что я узнал об уравнениях из школьных учебников

При решении уравнений кроме способа нахождения неизвестного компонента, мы использовали еще второй способ, при котором упрощали выражение, стоящее в левой части уравнения, используя свойства сложения, вычитания и умножения.

Рассмотрю несколько заданий из учебника.

№ 000. Решите двумя способами уравнение:

а) (х + 98) + 14 = 169; б) (35 + у) – 15 = 31 .

Решу первое уравнение двумя способами:

1) сначала найду неизвестное слагаемое х + 98:

а потом найду слагаемое х: х = 155 – 98,

2) сначала упростим выражение, стоящее в левой части уравнения, используя сочетательное свойство сложения

а затем найду неизвестное слагаемое х:

Решу второе уравнение двумя способами:

1) сначала найду неизвестное уменьшаемое 35 + у:

а потом найду слагаемое у: у = 46 – 35,

2) сначала упростим выражение, стоящее в левой части уравнения, используя свойство вычитания: (35 + у) – 15 = 31,

а затем найду неизвестное слагаемое у:

№ 000. Решите уравнение:

а) 3х + 5х + 96 = 1568;

Используя распределительное свойство умножения относительно сложения, упрощу левую часть первого и третьего уравнения, а распределительное свойство умножения относительно вычитания для второго и получу более простые уравнения. а) 8х + 96 = 1568;

б) 208z – 1843 = 11469;

После этого найду неизвестные компоненты: слагаемое, вычитаемое и множитель а) 8х + 96 = 1568,

х = 144. Ответ: 144.

б) 208z – 1843 = 11469,

208z = 11469 + 1843,

у = 167. Ответ: 167.

Еще в пятом классе я научился решать задачи с помощью уравнений.

Решу задачи из нашего учебника.

№ 000. Для школы купили 220 столов и стульев, причем стульев – в 9 раз больше, чем столов. Сколько столов и сколько стульев купили?

Решение. Пусть столов купили х штук, тогда стульев – 9х штук. Всего купили (х + 9х) штук, или 220. Получил уравнение: х + 9х = 220. Решу его. х + 9х = 220,

х = 22. Итак, купили 22 стола, тогда стульев – 229 = 198 .

№ 000(1). Первое число в 2,4 раза больше третьего, а второе число на 0,6 больше третьего числа. Найдите эти три числа, если их среднее арифметическое равно 2, 4.

Решение. Пусть третье число равно х, тогда 2,4х – первое число, а второе х + 0,6 . Среднее арифметическое этих чисел (2,4х + х + 0,6 + х) : 3 по условию задачи равно 2,4. Составлю уравнение и решу его.

(2,4х + х + 0,6 + х) : 3 = 2,4,

4,4х + 0,6 = 2,43,

1,5 –третье число, тогда 1,5 + 0,6 = 2,1 – второе число и 1,52,4 = 3,6 – первое число. Ответ: 3,6; 2,1 и 1,5.

Я провел маленькое исследование и убедился, что в учебнике «Математика – 5» достаточно много заданий, связанных с решением уравнений. Это задания первого вида: «Решите уравнение», «Угадайте корни уравнения» или «Найдите корни уравнения» и задания второго вида: «Решите задачу с помощью уравнения», «Придумайте задачу по уравнению», «Решите задачу».

372, 374, 375, 376, 379, 380, 395, 396, 439, 442, 445, 446, 462, 464, 482, 483, 485, 487, 490, 491, 496, 504, 505, 523, 524, 525 , 551, 568, 569, 570, 574, 576, 592, 593, 614, 615, 635, 639, 647, 660, 707, 727,

878, 1018, 1022, 1036, 1042, 1058, 1107, 1127, 1165, 1210, 1236, 1238, 1251, 1268, 1326, 1329, 1348, 1358, 1362, 1373, 1379, 1389, 1441, 1459, 1489, 1517, 1752, 1817.

373, 377, 397, 410, 440, 447, 484, 486, 489, 512, 526, 571,

572, 577, 578,579, 580, 581, 582, 583, 584, 585, 586, 587, 588, 589, 594, 602, 603, 607, 618, 619, 621, 622, 623, 624, 641, 643, 665, 669, 704, 705, 706, 726, 777, 837, 870, 871, 997, 1126, 1081, 1073, 1105,

1140, 1170, 1253, 1328, 1349, 1350, 1351, 1430,1460, 1461, 1462, 1463, 1490, 1491, 1558, 1559, 15 97, 1647, 1669, 1755, 1756, 1757, 1758, 1760, 1838, 1839, 1840.

То есть, 155 номеров всех заданий учебника, а их 1849, связаны с решением уравнений, то есть = 0, 083 829…. 8,4%. Но если учесть, что в данном учебнике первое задание, связанное с решением уравнения начинается с номера 372, то 1849 – 371 = 1478 и = 0, 10 487… 10%.

Теперь можно сделать вывод, что после изучения темы «Уравнение», каждое 10-е задание учебника требует умений решать уравнения. И это еще раз подчеркивает важность изучения темы «Уравнение»

Глава 3. Что я узнал об уравнении из дополнительной литературы.

3.1.Тайное становится явным (исследование)

Представьте, что в очень лёгком — практиче­ски невесомом — кошельке содержится какое-то количество монет одинакового достоинства. Как узнать, сколько монет в кошельке, не за­глядывая внутрь? Есть очень простой способ: положим кошелёк на одну чашу рычажных ве­сов и уравновесим его монетками на другой чаше. Сколько монет для этого потре­буется — столько же их и в кошельке.

В кошельке семь монет.

Весы — испытанный измерительный инструмент продавцов, химиков и аптекарей приходит на помощь и в чуть более сложном случае.

На левой чаше находящихся в равновесии весов лежат кошелёк с неизвестным числом монет и ещё 5 монет рядом с ним, а на правой чаше — 15 точно таких же монеток. Для того чтобы узнать, сколько монет в кошельке, снимем по 5 монет с обеих чаш — равновесие при этом не нарушится.

Следовательно, внутри кошелька 10 монет

Взгляд на уравнение как на равенство грузов на весах, на обеих чашах которых можно производить одинаковые преобразования, оказался очень плодотворным. В своём сочинении об уравнениях арабский учёный аль – Хорезми замечает, что равные количества можно не только прибавлять к обеим частям уравнения или вычитать из них. Равенство не нарушится и тогда, когда обе части умножаются или делятся на одно и то же число, если оно не равно нулю. Главный принцип: если над равными количествами произвести одинаковые действия, то в результате снова получатся равные количества – стал своеобразной «волшебной палочкой», которую обнаружили вдумчивые читатели руководства аль – Хорезми. Попробую и я воспользоваться этой палочкой, и насколько мне позволяют знания, исследовать и доказать, что аль – Хорезми был прав. Рассмотрю это на простом уравнении.

Проведу исследования и узнаю, на самом ли деле значение х = 19, останется везде одинаковым.

1) Прибавлю к обеим частям уравнения число 12, получу новое уравнение 2х + 28 + 12 = 66 + 12,

воспользуюсь правилом, что два соседних слагаемых можно заменять их суммой, тогда 2х + 40 = 78,

2) Вычту из обеих частей уравнения 16,

чтобы найти неизвестное уменьшаемое (2х + 28) нужно к разности прибавить вычитаемое 2х + 28 = 50 + 16,

1) Умножу обе части уравнения на 3,

(2х + 28) 3= 663,

воспользуюсь правилом, что при умножении суммы на число можно на него умножить каждое слагаемое в отдельности и полученные результаты сложить. 2х 3 + 28 3 = 198, применю правило, что от перестановки множителей произведение не изменяется, и получу 3 2х + 84 = 198,

4) Разделю обе части уравнения на 2,

(2х + 28) : 2 = 66 : 2,

Чтобы разделить сумму на число, можно разделить каждое слагаемое и полученные результаты сложить 2х : 2 + 28 :2 = 66 : 2,

Вывод: значение корня не изменится, если :

— к обеим частям уравнения прибавить или отнять одно и то же число;

— обе части уравнения умножить или разделить на число, неравное нулю.

Эти правила применяются для решения уравнений методом весов.

3.2. Способы решения уравнений.

Из дополнительной литературы я узнал о некоторых способах решения уравнений, с которыми я разобрался, и они оказались мне понятными.

а) Решение уравнений с помощью правила нахождения неизвестного компонента. Решение уравнений этим методом я подробно рассмотрел в главе 2.

б) Решение уравнений методом весов. Решение уравнений методом весов я рассматривал в главе «Исторические сведения».

Решу уравнения таким методом.

а) 4х – 9 = 2х + 11, в) 8х – 10 = 5х + 8,

из обеих частей уравнения из обеих частей уравнения

отнимем по 2х и прибавим 9, отнимем по 5х и прибавим 10,

получим уравнение получим уравнение

х = 20 : 2, х = 18 : 3,

Проверка. 4 10 – 9 = 2 10 + 11, Проверка. 8 6 – 10 = 56 + 8,

40 – 9 = 20 + 11, 48 – 10 = 30 + 8,

Ответ: х = 10. Ответ: х = 6.

Уравнения такого вида мы научимся решать в конце 6 класса, используя правила преобразования выражений, а пока их можно решать методом весов.

в) Решение уравнений методом проб и ошибок

а) Решите уравнение х (х + 3) = 70.

Никакие известные нам правила не помогают найти решение этого уравнения. Попробуем тогда подобрать решение «экспериментально», так называемым методом проб и ошибок.

Нам надо найти такое число х, чтобы значение выражения х(х + 3) было равно 70. Попробуем подставить в это выражение, например, х = 4: 4 (4 + 3) = 28. Мы видим, что выбранное число х слишком мало.

Возьмём теперь х = 6: 6 (6 + 3) = 54, и снова выбранное значение мало, хотя ближе к искомому. А следующая попытка оказывается удачной: при х = 7, имеем 7 (7 + 3) = 70. Значит, при х = 7 данное в условии равенство верно.

Казалось бы, уравнение уже решено, но это не так: ведь может оказаться, что буквенное выражение равно 70 при разных значениях букв. Поэтому нужны некоторые дополнительные рассуждения. Если бы число х было больше 7, то число х + 3 было больше 10, и тогда произведение оказалось бы больше 70. Точно так же число х не может быть меньше 7, иначе произведение будет меньше 70. Следовательно, среди натуральных чисел, есть только одно решение этого уравнения. Ответ: х = 7.

Итак, метод проб и ошибок позволяет найти ответ даже в случае, если уравнение представляет собой новый, не изученный ещё объект. Однако при использовании этого метода следует всегда помнить о том, что подбор одного решения не гарантирует полноты решения. Поэтому требуется дополнительное обоснование того, что найдены все возможные решения, и ни одно не пропущено.

г). Решение уравнений методом перебора.

При решении уравнений методом проб и ошибок мы видели, что простой подбор одного неизвестного числа не даёт уверенности в том, что найдены все искомые значения. В этом состоит существенный недостаток метода проб и ошибок.

Указанного недостатка лишен другой метод решения уравнений – метод полного перебора. При поиске неизвестного числа полным перебором рассматриваются все мыслимые возможности: если мы упустим хотя бы одну, то может оказаться, что именно она и даёт решение уравнение.

Полный перебор требует, как правило, больших усилий и большого времени. Однако внимательный анализ условия часто позволяет найти систему перебора, охватывающую все возможные варианты, но более короткую, чем просто перебор всех чисел по — порядку.

Например, глядя на уравнение х (х + 3) = 54, можно заметить, что его натуральные корни должны быть делителями числа 54. Значит, х может принимать лишь значения: 1, 2, 3,6, 9, 18, 27, 54. Подставляя эти числа вместо буквы х в уравнение, находим единственный корень х = 6.

Решим еще одно уравнение методом перебора.

Делители числа 20 – 1, 2, 4, 5, 10, 20.

Можно проанализировать и сделать вывод, что среди натуральных решений могут быть только числа большие 3, но меньшие 7. такими числами будут 4 и 5. проверим это.

х = 4, 4( 4 –– 4) = 4 13 = 12.

х = 5, 5(5 – 2)(7 – 5) = 52 2 = 20.

х= 5 – корень уравнения.

Если бы мы не делали анализа, то нам нужно было проверить все 6 чисел. А если число имеет много делителей, то перебор вариантов может оказаться слишком громоздким. Не всегда удаётся подобрать корни уравнения, и тем более доказать единственность решения. Может оказаться, что среди натуральных чисел решения нет, а среди других чисел оно есть.

Именно поэтому математики всегда стремились найти общие решения различных классов уравнений.

3.3. Математические фокусы.

В этом разделе я хочу показать, как с помощью уравнений отгадывать математические загадки и показывать математические фокусы. Основной темой математических фокусов являются угадывание задуманных чисел или результатов действий над ними. Весь секрет фокусов в том, что «отгадчик» знает и умеет использовать особые свойства чисел, а задумавший этих свойств не знает. Математический интерес каждого фокуса и заключается в разоблачении его теоретических основ, которые в большинстве случаев довольно просты, но иногда бывают хитро замаскированы. Рассмотрю один из математических фокусов. Фокусник предложил каждому из публики задумать число. Потом он сказал: «Прибавьте к задуманному числу 5. Теперь из результата вычтите 2. Теперь к результату прибавьте 7». Потом фокусник спросил у желающих, какое число получилось. Услышав ответ, он немедленно объявил каждому, какое число тот задумал. Этот фокус легко разгадать, если умеешь составлять и решать уравнения. Слева запишу задания «фокусника», а справа — выражения, которые он мысленно при этом составляет.

Задумайте число. Обозначаю его буквой х. Прибавьте к нему число 5. Получается число х + 5.

Из результата вычтите 2. Получается (х + 5) – 2.

К результату прибавьте 7. Получается ((х + 5) – 2) + 7. Скажите ваш результат. Допустим, он равен 17.

Приравнивая составленное выражение ((х + 5) – 2) + 7 к 17, получаю уравнение. ((х + 5) – 2) + 7 = 17, Упростим левую часть уравнения, воспользовавшись свойствами сложения и вычитания: ((х + 5) – 2) + 7 = (х + (5 – 2)) + 7 = (х + 3) + 7 = х + (3 + 7) = х + 10. Уравнение теперь получилось совсем простое : х + 10 = 17. Задуманное число х = 17 – 10, х = 7. Такие фокусы нетрудно придумать и самому. Например, эти два фокуса я придумал сам.

· Задумайте число, утройте его. Прибавьте к результату 10, а затем вычтите 1.Скажите, сколько получилось? А я скажу, какое число вы задумали (нужно от названного числа отнять 9 и результат разделить на 3).

· Задумайте число, прибавьте к нему 15, затем вычтите 7 и прибавьте задуманное число. Скажите, сколько получилось? А я скажу, какое число вы задумали (нужно от названного числа отнять 8 и результат разделить на 2).

Удивительной для непосвященных кажется способность отгадывать задуманное другим число. Но если вы узнаете секреты математических фокусов, то сможете не только их показывать, но и придумывать новые. Вы просите товарища задумать любое число, затем отнять от него 1, результат умножить на 2, из произведения вычисть задуманное число и сообщить вам результат. Прибавив к нему число 2, вы отгадаете задуманное. Секрет фокуса становится понятен, если записать предложенные действия в виде алгебраического выражения (x-1)2 – x, где x – задуманное число. Раскрыв скобки, и выполнив действия, мы получим, что это выражение равно x-2. Если ответ равен 23, то задумано число 21. Чтобы угадать задуманное число нужно от результата отнять 2

1.Задумайте число. Умножьте его на 3. К полученному прибавьте полученное разделите на 3. Скажите, сколько получилось?

Решение. (3х + 6) : 3 = х + 2. Чтобы получить задуманное число, нужно от названного числа отнять 2.

2. Задумайте число. Умножьте его на 4. Из полученного вычтите 3. Полученное умножьте на 3, К полученному прибавьте 5. Полученное разделите на 4. К полученному прибавьте 1. Скажите, сколько получилось? Решение. ((4х – 3)3 + 5) : 4 + 1 = (12х – 9 + 5) : 4 + 1 = ( 12х – (9 – 5)) : 4 + +1 = (12х – 4) : 4 + 1 = 3х – 1 + 1 = 3х – (1 – 1) = 3х – 0 = 3х.

Чтобы получить задуманное число, нужно названное число разделить на 3.

3. Задумайте число. Прибавьте к нему 3. Умножьте полученное на 6. Отнимите от полученного 3. Вычтите из полученного результата задуманное число. Полученное разделите на 5. Скажите”, сколько получилось?

Решение (( х + 3) 6 – 3 – х ) : 5 = ( 6х + 18 – 3 – х) : 5 = ( 5х + 15) : 5 = х + 3 . Чтобы получить задуманное число, нужно от названного числа отнять 3.

4. Задумайте любое число. Удвойте его. К полученному прибавьте 3. Полученное число умножьте на задуманное. От полученного результата отнимите задуманное. Полученное разделите на удвоенное задуманное число. Скажите, сколько получилось? Чтобы получить задуманное число, надо от названного числа отнять 1.

Очень эффектно выглядят фокусы на отгадывание даты рождения и возраста зрителей, особенно в малознакомой компании.

Возраст и дата рождения

Порядковый номер месяца рождения нужно умножить на 100 и к получившемуся произведению прибавить число месяца, на которое приходится день рождения. Затем полученную сумму нужно умножить на 2 и к тому, что получится, прибавить 8. Результат нужно умножить на 5, к произведению прибавить 4 и получившуюся сумму умножить на 10. К тому, что получится, остается прибавить полное число лет (возраст), увеличенное на 4. Пусть каждый, выполнивший все эти вычисления, запишет на листочке бумаги свою фамилию, получившееся число и передаст листочек вам. Получив эти листочки, вы по ним каждому можете сказать его возраст и дату рождения. Придется поступать так: из получившегося числа, записанного на листочке, каждый раз вычитайте по 444 и разность разбивайте на грани справа налево по две цифры в каждой. Первая грань справа даст возраст, вторая — число и третья — порядковый номер месяца рождения.

Работа над данной темой помогла узнать мне много нового из истории математики. Мне пришлось рассмотреть дополнительную математическую литературу, чтобы узнать что-то новое про уравнения, и я подтвердил гипотезу, что существуют различные способы решения уравнений.

Просмотрев все учебники по математики с 5 по 11 классы, я убедился в важности выбранной темы. В течение всех лет мы расширяем знания по теме «Уравнения». Я узнал решение более сложных уравнений с помощью правила

нахождения неизвестной компоненты и решение задач на составление уравнений, решал уравнения с применением их свойств, узнал названия уравнений: линейные, квадратные, дробно — рациональные, биквадратные, тригонометрические, иррациональные, показательные и логарифмические уравнений.

Конечно, эти названия мне ни о чём не говорят, но я теперь знаю, какие бывают уравнения, и что со временем я научусь их решать.

Мне было интересно узнать, что уравнения и математические фокусы, которые сейчас могут решать ученики 5-6 класса, в древности были по силам только математикам и мудрецам. И что, используя известные мне свойства сложения и умножения, я смог провести исследования и доказал на простых уравнениях, что значение корня не изменится, если:

— к обеим частям уравнения прибавить или вычесть одно и то же число;

— обе части уравнения умножить или разделить на число, неравное нулю.

Я научился решать более сложные уравнения, используя 4 способа, о них я прочитал в дополнительной литературе. При выполнении работы мне пришлось решить более 120 уравнений. Во время недели математики я показал математические фокусы в 5-х классах и в 3 – 4 классах.

Вместе с моим руководителем мы составили задания для одноклассников. Среди этих заданий есть те, для решения которых достаточно знаний, полученных на уроках. Но есть и такие уравнения, которые решаются новыми способами, о которых я рассказал в работе, то есть требуют дополнительных знаний. Это для тех ребят, кто захочет научиться решать уравнения, используя новые способы.

Я, думаю, что новые знания, которые я получил, пригодятся мне в дальнейшей учёбе. Все цели и задачи, которые я ставил перед собой, я выполнил.

Список использованной литературы

общеобразовательных учреждений. // М.: Мнемозина, 2005.

2. , БеленковаЕ. Ю. Математика 5 класс.

Задания для обучения и развития учащихся.// М.: Интеллект-

3. Математика: Учебник-собеседник для 5 – 6 классов средних школ//

Просвещение, 1989. (Б-ка учителя математики), стр.187

4. , и др. Математика. Учебник для 4 класса нач.

Школы в 2 ч. Ч. 2. (Второе полугодие) – М.: Просвещение, 2005.

5. Энциклопедический словарь юного математика //

Сост. . М.: Педагогика, 1985, стр.345

6. Энциклопедия для детей. Т. 11. Математика // Ред. коллегия:

М. Аксёнова, В. Володин и др. – М.: Аванта, 2005, стр.237

Видео:Зачем нужна математикаСкачать

Математические уравнения и их использование в решении задач

Видео:1. Что такое дифференциальное уравнение?Скачать

Математические уравнения и их использование в решении задач

Глава 1. История возникновения уравнений

Глава 2. Решения уравнений и способы их упрощения

Глава 3. Использование уравнений при решении задач

Математическое образование, получаемое в общеобразовательной школе, является важнейшим компонентом общего образования и общей культуры современного человека. Практически все, что окружает современного человека – это все так или иначе связано с математикой. А последние достижения в физике, технике и информационных технологиях не оставляют никакого сомнения, что и в будущем положение вещей останется прежним. Поэтому решение многих практических задач сводится к решению различных видов уравнений, которые необходимо научиться решать.

Уравнения в школьном курсе алгебры занимают ведущее место. На их изучение отводится времени больше, чем на любую другую тему. Действительно, уравнения не только имеют важное теоретическое значение, но и служат чисто практическим целям. Подавляющее большинство задач о пространственных формах и количественных отношениях реального мира сводится к решению различных видов уравнений. Овладевая способами их решения, мы находим ответы на различные вопросы из науки и техники (транспорт, сельское хозяйство, промышленность, связь и т. д.).

Глава 1. История возникновения уравнений

Алгебра как искусство решать уравнения зародились очень давно в связи с потребностью практики, в результате поиска общих приёмов решения однотипных задач. Самые ранние дошедшие до нас рукописи свидетельствуют о том, что в Древнем Вавилоне и Древнем Египте были известны приёмы решения линейных уравнений. Слово «алгебра» возникло после появления тракта «Китаб аль-джебр валь-мукабала» хорезмского математика и астронома Мухамеда Бен Муса аль Хорезми. Термин «аль-джерб», взятый из названия этой книги, в дальнейшем стал употребляться как алгебра.

Знак равенства ввел в 1556 году английский математик Рекорд, который объяснил это так, что ничто не может быть более равным, чем два параллельных отрезка.

Франсуам Виемт (фр. Franзois Viиte, seigneur de la Bigotiиre; 1540 — 13 декабря 1603) — выдающийся французский математик, один из основоположников алгебры

Создателем современной буквенной символики является французский математик Франсуа Виет (1540 — 1603). До XVI в. изложение алгебры велось в основном словесно. Буквенные обозначения и математические знаки появлялись постепенно.

Знаки + — впервые встречаются у немецких алгебраистов XVI в. Несколько позже вводится знак * для умножения. Знак деления (:) был введён лишь в XVII в. Решительный шаг в использовании алгебраической символики был сделан в XVI в., когда французский математик Франсуа Виет (1540-1603) и его современники стали применять буквы для обозначения не только неизвестных (что делалось и ранее), но и любых чисел. Однако эта символика ещё отличалась от современной. Так, Виет для обозначения Неизвестного числа применял букву N (Numerus-число), для квадрата и куба неизвестного буквы Q (Quadratus — квадрат) и C (Cubus — куб). Например, запись уравнения X в кубе, минус 8X в квадрате, плюс 16X, равно 40 у Виета выглядела бы так: 1C-8Q+16N aequ. 40 (aequali — равно). Виет делит изложение на две части: общие законы и их конкретно-числовые реализации. То есть он сначала решает задачи в общем виде, и только потом приводит числовые примеры. В общей части он обозначает буквами не только неизвестные, что уже встречалось ранее, но и все прочие параметры, для которых он придумал термин «коэффициенты» (буквально: содействующие). Виет использовал для этого только заглавные буквы: гласные для неизвестных, согласные для коэффициентов. Виет свободно применяет разнообразные алгебраические преобразования. Например, замену переменных или смену знака выражения при переносе его в другую часть уравнения.

Новая система позволила просто, ясно и компактно описать общие законы арифметики и алгоритмы. Символика Виета была сразу же оценена учёными разных стран, которые приступили к её совершенствованию. Диофант (не ранее III века н.э.) — единственный известный нам древнегреческий математик, который занимался алгеброй.

Он решал различные уравнения, особое внимание уделял неопределенным уравнениям, теория которых называется теперь «диофантовым анализом». У Диофанта была попытка ввести буквенную символику.

Первая книга предварена обширным введением, в котором описаны используемые Диофантом обозначения. Неизвестную Диофант называет «числом» и обозначает буквой т, квадрат неизвестной — символом дн (сокращение от дэнбмйт — «степень»). Предусмотрены специальные знаки для следующих степеней неизвестного, вплоть до шестой, называемой кубо-кубом, и для противоположных им степеней. Знака сложения у Диофанта нет: он просто пишет рядом положительные члены, причём в каждом члене сначала записывается степень неизвестного, а затем численный коэффициент

Эваримст Галуам (фр. Йvariste Galois;25 октября 1811, 25 октября 1811, Бур-ля-Рен, О-де-Сен, Франция — 31 мая 1832, ,Франция) — выдающийся французский математик, основатель современной высшей алгебры.

Эврист Галуа (1811 — 1832) — этот гениальный математик погиб на дуэли, подстроенной его врагами. В ночь перед дуэлью он написал письмо, в котором изложил свои результаты, давшей начало целой науке — «теории Галуа»

Нильс Хенрик Абель (1802 — 1829) внес важный вклад в теорию уравнений. В 1824 году он опубликовал доказательство неразрешимости в радикалах общего буквенного выражения пятой степени.

«Абель оставил математикам столь богатое наследие, что им будет чем заниматься в ближайшие 150 лет» (Шарль Эрмит). Нильс Хенрик Абель (норв. Niels Henrik Abel; 5 августа 1802, Фингё — 6 апреля 1829, Фроланд близ Арендаля) — знаменитый норвежский математик

1.Из истории возникновения уравнений.

Алгебра возникла в связи с решением разнообразных задач при помощи уравнений. Обычно в задачах требуется найти одну или несколько неизвестных, зная при этом результаты некоторых действий, произведенных над искомыми и данными величинами. Такие задачи сводятся к решению одного или системы нескольких уравнений, к нахождению искомых с помощью алгебраических действий над данными величинами. В алгебре изучаются общие свойства действий над величинами.

2. Содержание и роль линии уравнений в современном школьном курсе математики

Материал, связанный с уравнениями, составляет значительную часть школьного курса математики. Это объясняется тем, что уравнения широко используются в различных разделах математики, в решении важных прикладных задач.

Истоки алгебраических методов решения практических задач связаны с наукой древнего мира. Как известно из истории математики, значительная часть задач математического характера, решаемых египетскими, шумерскими, вавилонскими писцами-вычислителями (XX—VI вв. до н. э.), имела расчетный характер. Однако уже тогда время от времени возникали задачи, в которых искомое значение величины задавалось некоторыми косвенными условиями, требующими, с нашей современной точки зрения, составления уравнения или системы уравнений. Первоначально для решения таких задач применялись арифметические методы. В дальнейшем начали формироваться начатки алгебраических представлений. Например, вавилонские вычислители умели решать задачи, сводящиеся с точки зрения современной классификации к уравнениям второй степени. Таким образом, был создан метод решения текстовых задач, послуживший в дальнейшем основой для выделения алгебраического компонента и его независимого изучения.

Это изучение осуществлялось уже в другую эпоху сначала арабскими математиками (VI—Х вв. н. э.), выделившими характерные действия, посредством которых уравнения приводились к стандартному виду (приведение подобных членов, перенос членов из одной части уравнения в другую с переменой знака), а затем европейскими математиками Возрождения, в итоге длительного поиска создавшими язык современной алгебры (использование букв, введение символов арифметических операций, скобок и т. д.). На рубеже XVI—XVII вв. алгебра как специфическая часть математики, обладающая своим предметом, методом, областями приложения, была уже сформирована. Дальнейшее ее развитие, вплоть до нашего времени, состояло в совершенствовании методов, расширении области приложений, уточнении понятий и связей их с понятиями других разделов математики. В этом процессе все яснее становилась важность роли, которую играло понятие уравнения в системе алгебраических понятий.

Открытие координатного метода (Декарт, XVII в.) и последовавшее за ним развитие аналитической геометрии позволили применить алгебру не только к задачам, связанным с числовой системой, но и к изучению различных геометрических фигур. Эта линия развития алгебры упрочила положение уравнения как ведущего алгебраического понятия, которое связывалось теперь уже с тремя главными областями своего возникновения и функционирования:

1) уравнение как средство решения текстовых задач;

2) уравнение как особого рода формула, служащая в алгебре объектом изучения;

3) уравнение как формула, которой косвенно определяются числа или координаты точек плоскости (пространства), служащие его решением.

Каждое из этих представлений оказалось в том или ином отношении полезным.

Таким образом, уравнение как общематематическое понятие много аспектно, причем ни один из аспектов нельзя исключить из рассмотрения, особенно если речь идет о проблемах школьного математического образования.

Ввиду важности и обширности материала, связанного с понятием уравнения, его изучение в современной методике математики организовано в содержательно — методическую линию — линию уравнений и неравенств. Здесь рассматриваются вопросы формирования понятий уравнения и неравенства, общих и частных методов их решения, взаимосвязи изучения уравнений и неравенств с числовой, функциональной и другими линиями школьного курса математики. Выделенным областям возникновения и функционирования понятия уравнения в алгебре соответствуют три основных направления развертывания линии уравнений и неравенств в школьном курсе математики.

а) Прикладная направленность линии уравнений раскрывается главным образом при изучении алгебраического метода решения текстовых задач. Этот метод широко применяется в школьной математике, поскольку он связан с обучением приемам, используемым в приложениях математики.

В настоящее время ведущее положение в приложениях математики занимает математическое моделирование. Используя это понятие, можно сказать, что прикладное значение уравнений, их систем определяется тем, что они являются основной частью математических средств, используемых в математическом моделировании.

б) Теоретико-математическая направленность линии уравнений раскрывается в двух аспектах: во-первых, в изучении наиболее важных классов уравнений, и их систем и, во-вторых, в изучении обобщенных понятий и методов, относящихся к линии в целом. Оба эти аспекта необходимы в курсе школьной математики. Основные классы уравнений связаны с простейшими и одновременно наиболее важными математическими моделями. Использование обобщенных понятий и методов позволяет логически упорядочить изучение линии в целом, поскольку они описывают то общее, что имеется в процедурах и приемах решения, относящихся к отдельным классам уравнений, неравенств, систем. В свою очередь, эти общие понятия и методы опираются на основные логические понятия: неизвестное, равенство, равносильность, логическое следование, которые также должны быть раскрыты в линии уравнений

в) Для линии уравнений характерна направленность на установление связей с остальным содержанием курса математики

Эта линия тесно связана с числовой линией. Основная идея, реализуемая в процессе установления взаимосвязи этих линий,— это идея последовательного расширения числовой системы. Все числовые области, рассматриваемые в школьной алгебре и началах анализа, за исключением области всех действительных чисел, возникают в связи с решением каких-либо уравнений и их систем. Области иррациональных и логарифмических выражений связаны соответственно с уравнениями хk = b (k — натуральное число, большее 1) и ax=b.

Линия уравнений тесно связана также и с функциональной линией. Одна из важнейших таких связей — приложения методов, разрабатываемых в линии уравнений, к исследованию функции (например, к заданиям на нахождение области определения некоторых функций, их корней, промежутков знакопостоянства и т. д.). С другой стороны, функциональная линия оказывает существенное влияние как на содержание линии уравнений и неравенств, так и на стиль ее изучения. В частности, функциональные представления служат основой привлечения графической наглядности к решению и исследованию уравнений, неравенств и их систем.

3. О трактовке понятия уравнения.

Понятие уравнения относится к важнейшим общематематическим понятиям. Именно поэтому затруднительно предложить его определение, одновременно и строгое с формальной точки зрения, и доступное для учащихся, приступающих к овладению школьным курсом алгебры.

Логико-математическое определение уравнения можно привести в такой форме: пусть на множестве М зафиксирован набор алгебраических операций, х — переменная на М; тогда уравнением на множестве М относительно х называется предикат вида а(х)=b (х), где а(х) и b(х)-термы относительно заданных операций, в запись которых входит символ х. Аналогично определяется уравнение от двух переменных и т. д.

Принятым в логике терминам «терм» и «предикат» соответствуют термины школьной математики «выражение» и «предложение с переменной». Поэтому наиболее близко к приведенному формальному определению следующее определение: «Предложение с переменной, имеющее вид равенства между двумя выражениями с этой переменной, называется уравнением»

Анализируя приведенное математическое определение уравнения, можно выделить в нем два компонента. Первый состоит в том, что уравнение — это особого рода предикат. Второй уточняет, какого именно рода: это равенство, соединяющее два терма, причем термы также имеют определенный специальный вид. При изучении материала, относящегося к линии уравнений и неравенств, оба компонента играют значительную роль.

Первый — смысловой компонент, важен прежде всего для уяснения понятия корня уравнения. Кроме того, смысловой компонент почти всегда используется при обосновании корректности того или иного преобразования уравнения.

Второй компонент относится к формальным особенностям записи, изображающей уравнение. Назовем этот компонент знаковым. Он важен в случаях, когда запись уравнения подвергается различным преобразованиям: зачастую такие преобразования производятся чисто механически, без обращения к их смыслу.

Возможность использования в школьном обучении подхода к понятию уравнения, включающего явно упоминание о предложении с переменной, зависит от присутствия этого термина и терминов «истина», «ложь» в обязательном материале курса математики. Если их нет, то привести подобное определение невозможно. В этом случае смысловой компонент понятия уравнения переходит в определение другого понятия, тесно связанного с понятием уравнения, — корня уравнения. Получается система из двух терминов: термин «уравнение» несет в себе признаки знакового компонента, а термин «корень уравнения» учитывает смысловой компонент. Такое определение приведено, например, в учебнике Колмогорова А. Н.

Часто, особенно в начале систематического курса алгебры, понятие уравнения вводится посредством выделения его из алгебраического метода решения задач. В этом случае независимо от того, каков текст определения, существенным оказывается подход к понятию уравнения, при котором оно представляет косвенную форму задания некоторого неизвестного числа, имеющего в соответствии с сюжетом задачи конкретную интерпретацию. Например, понятие уравнения вводится на материале текстовой задачи: «Конверт с новогодней открыткой стоит 170сум. Конверт дешевле открытки на 70 сумк. Найти стоимость открытки». Переход к определению уравнения осуществляется на основе анализа некоторых формальных особенностей записи: х+(х-70)= 170, выражающей содержание данной задачи в алгебраической форме. С помощью этого же сюжета вводится и понятие корня уравнения. Вот эти определения: «Равенство, содержащее неизвестное число, обозначенное буквой, называется уравнением. Корнем уравнения называется то значение неизвестного, при котором это уравнение обращается в верное равенство». Указанный способ введения понятия уравнения соответствует еще одному компоненту понятия уравнения — прикладному.

Еще один подход к определению понятия уравнения получается при сопоставлении области определения уравнения и множества его корней. Обычно множество корней уравнения — собственное подмножество его области определения. С другой стороны, при решении уравнений приходится использовать преобразования, которые опираются на тождества, т. е. на равенства, истинные на всей области определения. Выделенное здесь противопоставление тождества и уравнения может быть положено в основу определения уравнения: «Буквенное равенство, которое не обязательно превращается в верное численное равенство при допустимых наборах букв, называется уравнением»

Формирование понятия уравнения требует использования еще одного термина: «решить уравнение». Различные варианты его определения отличаются друг от друга, по существу, только наличием или отсутствием в них термина «множество».

Таким образом, при освоении понятия уравнения необходимо использовать термины «уравнение», «корень уравнения», «что значит решить уравнение». При этом наряду с компонентами понятия уравнения, входящими в текст определения, надо включать и все другие его компоненты по мере развертывания материала данной линии.

В определении понятия уравнения используется один из двух терминов: «переменная» или «неизвестное». Различие между ними состоит в том, что переменная пробегает ряд значений, не выделяя ни одного из них специально, а неизвестное представляет собой буквенное обозначение конкретного числа (поэтому этим термином удобно пользоваться при составлении уравнений по текстовым задачам). Вопросы, связанные с выбором одного их этих терминов для использования в школьной практике, в настоящее время еще нельзя считать окончательно решенными. Выбор того или иного из них влечет определенные различия в развертывании содержания линии уравнений и неравенств. Так, с термином «переменная» связана операция подстановки числа вместо буквы, поэтому в уравнение а(х) = b(х) можно подставлять вместо х конкретные числа и находить среди них корни. Термин же «неизвестное» обозначает фиксированное число; подставлять число на место буквы, обозначающей неизвестное, поэтому нелогично. Нахождение корней уравнения а(х) = b(х) с этой точки зрения должно осуществляться с помощью действий, при которых это равенство рассматривают как верное и пытаются привести его к виду х = х, где х — числовое выражение.

При описании методики мы будем пользоваться термином «неизвестное», который ближе, чем «переменная», связан с алгебраическим методом решения текстовых задач и тем самым с прикладной направленностью линии уравнений и неравенств.

Глава 2. Решения уравнений и способы их упрощения

Наука математика возникла на первых этапах развития человечества из его практических нужд и творческих потребностей. Герман Вейль писал: «Математика играет весьма существенную роль в формировании нашего духовного облика. Занятие математикой — подобно мифотворчеству, литературе или музыке — это одна из наиболее присущих человеку областей и его творческой деятельности, в которой проявляется его человеческая сущность, стремление к интеллектуальной сфере жизни, являющейся одним из проявлений мировой гармонии».

В настоящее время математика достигла своего расцвета, она является основой большинства современных наук, а ее приложения используются во всех областях человеческой деятельности.

Большим значением в практической математике является метод уравнений. С их помощью решаются множество различных задач смежных дисциплин и задач прикладного характера (экономические, транспортные, биохимические, астрономические, географические и многие другие)

Чтобы решить уравнение нужно совершить ряд алгебраических преобразований. В математике существует множество задач, которые решаются с помощью уравнений. Чтобы решить эти задачи, мы вспоминаем слова великого Ньютона, задачу нужно перевести с родного языка на язык алгебры.

Используя данный способ, мы сможем легко и быстро решить любую, на первый взгляд сколь угодно сложную, задачу.

Опираясь на данное изложение, мы хотели бы сказать, что современный мир — мир развития науки и техники, невозможен без знания и умения решать уравнения.

Уравнением с одним неизвестным называется запись вида, А (х)=В (х) — выражения от неизвестного х. В эти выражения помимо чисел, знаков арифметических операций и обозначений функций могут входить и другие буквы, которые обозначают переменные, называемые параметрами.

Областью определения уравнения (иногда говорят — область допустимых значений неизвестного) называется множество всех значений х, при которых определены обе части уравнения.

Корнем или решением, уравнения называется значение неизвестного, при подстановке которого в уравнении получается верное числовое равенство. Решить уравнение — значит найти все его корни или доказать, что их нет.

Есть несколько видов уравнений, которые решаются по готовым формулам. Это линейные и квадратные уравнения, а также уравнения вида f (х)=а, где f — одна из стандартных функций (степенная или показательная функция, логарифм, синус, косинус, тангенс или котангенс). Такие уравнения считаются простейшими. Например, корень уравнения х 3 =а равен, корень уравнения log ₃х = а есть 3 а , а уравнение cos х = а решается по формуле х= arcos, а + 2Пп, где п=о, 1, 2,…Существует формула и для кубического уравнения, но его к простейшим не относят.

Так вот, главная задача при решении любого уравнения — свести его к простейшим.

Два основных способа упрощения уравнений — это замена переменной и разложение на множители.

Например, биквадратное уравнение х 4 +ах 2 +b=0 сводится к квадратному заменой y=х 2 , а тригонометрическое уравнение 2cos 2 х +cos х — 1= 0 — заменой y= cos х. вообще, если вы сумели записать уравнение в виде F (f (x))=0, сделайте замену y=f (x). Решить два уравнения, f (y)=0 и f (x)=y, почти всегда проще, чем одно данное.

Разложить уравнение на множители — значит представить его в виде f (x) . g (x)=0. Такое уравнение можно заменить совокупностью двух уравнений: f (x)=0 и g (x)=0. Множеством решений исходного уравнения будет объединение множеств решений этих двух более простых. Правда, здесь спрятана и одна из ловушек. При замене одного уравнения двумя может расшириться область определения задачи: первое уравнение определено на пересечении областей определения f и g, а совокупность двух уравнений — на объединении. Так, уравнение (х+1)=0 имеет только один корень (х=0), совокупность же уравнений =0 и х+1=0 — два (х=0 и х= -1).

Один корень легко угадать: х= -1.

Как найти остальные? Можно доказать, что если х₀ — корень многочлена P (х), то это многочлен делится на х — х₀, т. е.разлагается на множители, один из которых х — х₀. Выполним это разложение — вынесем из левой части множитель х+1:

х 2 — 3х — 2=х 3 +х 2 — х 2 — 3х — 2= х 2 (х+1) — (х 2 +х) — 2х — 2= (х+1) (х 2 -х -2).

Обратим внимание на используемый при этом прием — прибавление и вычитание одного и того же выражения (…=х 2 — х…). Этот нехитрый, но очень полезный прием носит шутливое название «метод Тараса Бульбы» (вспомним: «Я тебя породил, я тебя и убью!»). Ну, а дальше остается решить квадратное уравнение.

Таковы главные способы упрощения. Однако догадаться какую именно замену следует применить или как разложить на множители конкретное уравнение, порой бывает очень трудно. Успех здесь зависит от знания стандартных формул, опыта, смекалки и в большой мере — от удачи.

Глава 3. Использование уравнений при решении задач

Язык алгебры — уравнения. «Чтобы решить вопрос, относящийся к числам или к отвлеченным отношениям величин, нужно лишь перевести задачу с родного языка на язык алгебраический», — писал великий Ньютон в своем учебнике алгебры, озаглавленном «Всеобщая арифметика». Как именно выполняется такой перевод с родного языка на алгебраический, Ньютон показал на примерах. Вот один из них:

🎬 Видео

О чем говорят уравнения Максвелла? Видео 1/2Скачать

Дарья Лыткина - История квадратных уравнений | РНАСкачать

Ал-Хорезми и квадратные уравненияСкачать

Как распознать талантливого математикаСкачать

Математика - Откуда берется формула дискриминанта?Скачать

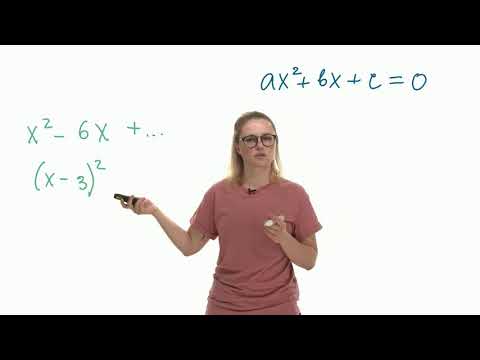
Решение задач с помощью дробно рациональных уравненийСкачать

Математика не нужна!Скачать

Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

Зачем нужен ИНТЕГРАЛ. Объяснение смыслаСкачать

Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

Заземление. Кто придумал? Зачем? Какие бывают системы заземления. Мощный #энерголикбезСкачать

Квадратное уравнение. 1 урок.Скачать

Как решают уравнения в России и США!?Скачать

Можно ли решить уравнение 5-й степени? – математик Алексей Савватеев | НаучпопСкачать