В аналитической геометрии всякому уравнению вида F(x; у) = 0 может соответствовать некоторая линия, свойства которой определяются данным уравнением.
Под F(x; у) = 0 понимаем многочлен степени n; степень многочлена n – порядок линии.
Значит, кривая первого порядка, в декартовой системе координат, описывается алгебраическим уравнением первого порядка ax + by + c = 0, где хотя бы один из коэффициентов a или b отличен от нуля. Это уравнение называют также линейным уравнением. А само выражение, типа ax+by+c=0 и a 2 +b 2 ≠ 0, принято обозначать как общее уравнение прямой.
Следовательно, любая прямая на плоскости представляет собой алгебраическую кривую первого порядка и любая алгебраическая кривая первого порядка на плоскости есть прямая.
Общее уравнение кривой второго порядка в декартовых координатах имеет вид:
причем, в зависимости от значения произведение аb получаем:
— эллипс, частный случай — окружность ( когда ab > 0);
Видео:Лекция 22. Декартова система координат на плоскости и полярная система координатСкачать

Упражнения
1. Нарисуйте кривую, задаваемую уравнением r = sin 4 φ .
2. Нарисуйте кривую, задаваемую уравнением r = cos φ .
3. Для параболы x 2 = 4 ay выберем в качестве полярной оси луч, идущий по оси Oy с началом в фокусе F (0, a ) параболы. Переходя от декартовых к полярным координатам, покажите, что парабола с выколотой вершиной задается уравнением

4. Докажите, что уравнение

задает эллипс, если 0 

5. Нарисуйте спираль Архимеда, заданную уравнением r = — φ . Чему равно расстояние между соседними витками этой спирали?
6. Человек идет с постоянной скоростью вдоль радиуса вращающейся карусели. Какой будет траектория его движения относительно земли?
7. Нарисуйте гиперболическую спираль , задаваемую уравнением r = 
8. Нарисуйте спираль Галилея , которая задается уравнением r = a 
9. Нарисуйте кривую, задаваемую уравнением r = | 
10. Нарисуйте кривую, задаваемую уравнением r = 
11. Нарисуйте кривую, задаваемую уравнением r = 
12. Найдите параметрические уравнения: а) спирали Архимеда; б) логарифмической спирали.
1. Березин В. Кардиоида //Квант. – 1977. № 12.
2. Березин В. Лемниската Бернулли //Квант. – 1977. № 1.
3. Берман Г.Н. Циклоида. – М.: Наука, 1975.
4. Бронштейн И. Эллипс. Гипербола. Парабола / Такая разная геометрия. Составитель А.А. Егоров. – М.: Бюро Квантум, 2001. — / Приложение к журналу «Квант» № 2/2001.
5. Васильев Н.Б., Гутенмахер В.Л. Прямые и кривые. – 3-е изд. – М.: МЦНМО, 2000.
6. Маркушевич А.И. Замечательные кривые. – М.- Л.: Гос. изд. течн. – теор. лит., 1951. — / Популярные лекции по математике, выпуск 4.
7. Савелов А.А. Плоские кривые. – М.: ФИЗМАТЛИТ, 1960.
8. Смирнова И.М., Смирнов В.А. Кривые. Курс по выбору. 9 класс. – М.: Мнемозина, 2007.
9. Смирнова И.М., Смирнов В.А. Геометрия. Учебник для 7-9 классов общеобразовательных учреждений. – М.: Мнемозина, 2011.
10. Смирнова И.М., Смирнов В.А. Компьютер помогает геометрии. – М.: Дрофа, 2003.
Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Примеры решений: полярная система координат
В этом разделе вы найдете бесплатные примеры решений задач по аналитической геометрии на плоскости на тему Кривые в полярной системе координат: табуляция функции, построение графика, переход к уравнению в декартовой системе координат т.п.
Основные этапы при работе с кривой, заданной в полярной системе координат, такие:
- 1. Построить полярную систему координат (изобразить полюс, полярную ось и угловые направления). Обычно строят вспомогательные лучи через $pi/6$ или $pi/8$ радиан, для большинства кривых этих точек (получается от $0$ до $2pi$ помещается 12 или 16 значений) вполне достаточно.
- 2. Табулируем кривую: берем последовательно все углы $phi$ (см. выше): $0$, $pi/8$, $pi/4$, $3pi/8$. и в каждой точке вычисляем значение $rho(phi)$. Заносим значения в таблицу.
- 3. Берем начерченную в первом пункте полярную систему координат и наносим точки. На полярной оси отмеряем значние $rho(0)$, на луче $pi/8$ — $rho(pi/8)$ и так далее.
- 4. Соединяем все точки плавной линией. Получается искомая кривая. Для проверки правильности можно построить дополнительно график с помощью онлайн-сервисов.
- 5. Если требуется найти уравнение кривой в декартовой системе координат, подставляем подходящие формулы $rho=sqrt$, $x=rhocos phi$, $y=rhosin phi$ и преобразуем.
Более подробно — в примерах ниже. Удачного изучения!
Видео:Построение кривой в полярной системе координатСкачать

Полярная система координат: решения онлайн
Задача 1. Построить следующие кривые в полярной системе координат: Лемниската Бернулли $rho^2=2cos 2phi$ (полюс помещен в точку О).
Задача 2. Построить по точкам кривую, заданную уравнением в полярной системе координат $rho=2sin 2phi$. Найти уравнение кривой в прямоугольной системе координат, начало которой совмещено с полюсом, а положительная полуось $Ox$ с полярной осью.
Задача 3. Дана линия своим уравнением в полярной системе координат $r=8 sin phi$. Требуется:
1) построить линию по точкам, давая $phi$ значения через $pi/6$, начиная с 0 до $2pi$.
2) Найти уравнение этой линии в декартовой прямоугольной системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс с полярной осью.
Задача 4. Линия задана уравнением $r=18/(4+5cos phi)$ в полярной системе координат. Требуется:
Построить линию по точкам, начиная от 0 до $2pi$ и придавая $phi$ значения через промежуток $pi/8$.
Найти уравнение данной линии в декартовой прямоугольной системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс – с полярной осью.
Назвать линию, найти координаты фокусов и эксцентриситет.
🎥 Видео
Поворот и параллельный перенос координатных осей. ЭллипсСкачать
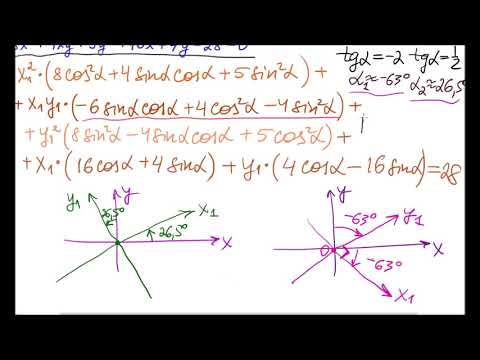
Полярная система координатСкачать

Математика Без Ху!ни. Полярные координаты. Построение графика функции.Скачать

Математика без Ху!ни. Уравнение плоскости.Скачать

§30 Уравнения кривых второго порядка в полярных координатахСкачать

Лекция 31.1. Кривые второго порядка. ЭллипсСкачать

Видеоурок "Преобразование координат"Скачать

Лекция 23. Виды уравнений прямой на плоскости.Скачать

§31.1 Приведение уравнения кривой к каноническому видуСкачать

Аналитическая геометрия: Эллипс, Парабола, Гипербола. Высшая математикаСкачать

Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Координаты на плоскости и в пространстве. Вебинар | МатематикаСкачать

Полярная система координатСкачать

Видеоурок "Общее уравнение кривой 2 порядка"Скачать

Лекция по АнГем: Кривые на плоскости.Скачать

9 класс, 7 урок, Уравнение прямойСкачать

Видеоурок "Полярная система координат"Скачать
