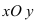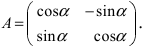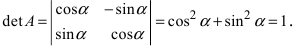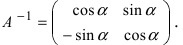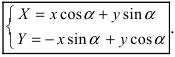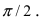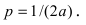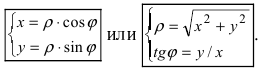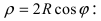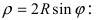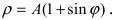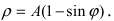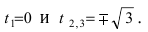Кривая задана общим уравнением найти угол поворота канонической системы координат в градусах (3 видео)

Приведение кривой второго порядка к каноническому виду

Пример . Дано уравнение кривой 3x 2 +10xy+3y 2 -2x-14y-13=0 в системе координат (0,i,j), где i =(1,0) и j =(0,1).
1. Определить тип кривой.
2. Привести уравнение к каноническому виду и построить кривую в исходной системе координат.
3. Найти соответствующие преобразования координат.

Решение. Приводим квадратичную форму B=3x 2 +10xy+3y 2 к главным осям, то есть к каноническому виду. Матрица этой квадратичной формы . Находим собственные числа и собственные векторы этой матрицы:

Характеристическое уравнение:
; λ₁=-2, λ₂=8. Вид квадратичной формы: .
Исходное уравнение определяет гиперболу.
Заметим, что вид квадратичной формы неоднозначен. Можно записать 8x₁ 2 -2y₁ 2 , однако тип кривой остался тот же – гипербола.
Находим главные оси квадратичной формы, то есть собственные векторы матрицы B. .
Собственный вектор, отвечающий числу λ=-2 при x₁=1: x ₁=(1,-1).
В качестве единичного собственного вектора принимаем вектор , где – длина вектора x ₁.
Координаты второго собственного вектора, соответствующего второму собственному числу λ=8, находим из системы
.
x ₂=(1,1); .
Итак, имеем новый ортонормированный базис ( i ₁, j ₁).
По формулам (5) пункта 4.3.3. переходим к новому базису:
или

Задание. Привести к каноническому виду уравнение линии 17x 2 + 12xy + 8y 2 — 20 = 0.
Решение.Пример 2

Задание. Привести к каноническому виду уравнение линии второго порядка, используя теорию квадратичных форм и определить её вид. Уравнение кривой второго порядка путем выделения полного квадрата привести к каноническому виду. Решение

Задание. Привести уравнение к каноническому виду: 16x 2 — 9y 2 -64x — 8y +199 = 0.
Решение.Скачать решение

Задание. Установить, что каждое из следующих уравнений определяет гиперболу, и найти координаты ее центра С, полуоси, эксцентриситет, уравнения асимптот и уравнения директрис. Изобразить гиперболу на чертеже, указав фокусы, асимптоты и директрисы.
Решение:Скачать решение

Задание. Установить, что каждое из следующих уравнений определяет эллипс, и найти координаты его центра С, полуоси, эксцентриситет, уравнения директрис. Изобразить эллипс на чертеже, указав оси симметрии, фокусы и директрисы.
Решение:Скачать решение

Содержание

Преобразования декартовой системы координат с примерами решения
Преобразования декартовой системы координат
Параллельный перенос и поворот системы координат
Полярные координаты. Замечательные кривые
Примеры решений: кривые второго порядка
Кривые 2-го порядка: решения онлайн
🎬 Видео

Видео:Поворот координатных осей. Пара мнимых прямыхСкачать

Преобразования декартовой системы координат с примерами решения

Содержание:

Видео:Математика Без Ху!ни. Полярные координаты. Построение графика функции.Скачать

Преобразования декартовой системы координат

Параллельный перенос и поворот системы координат

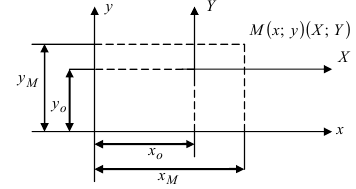
1. Параллельный перенос системы координат. Пусть на плоскости две декартовы системы координат, причем соответствующие оси параллельны и сонаправлены (Рис.46):

Рис. 46. Параллельный перенос одной системы координат относительно другой системы.

Систему координат

Пример:

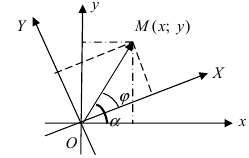
Дана точка М(3;2) и начало новой системы координат 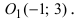Вычислить положение точки М в новой системе отсчета.

Решение:

Используя формулы, определяющие параллельный перенос одной системы отсчета относительно другой, получим 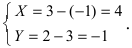Следовательно, точка М в новой системе отсчета имеет координаты М(4; -1).

2. Поворот системы координат. Пусть даны две системы координат (старая и новая), имеющие общее начало отсчета и повернутые относительно друг друга на угол 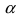(Рис. 47):

Рис. 47. Поворот одной системы координат относительно другой системы с общим началом координат двух систем.

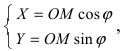
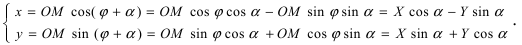
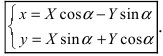
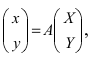
Получим формулы, связывающие старые и новые координаты произвольной точки М(х; у). Из рисунка видно, что в новой системе координат координаты точки равны а координаты этой точки в старой системе координат равны Таким образом формулы перехода от новых координат произвольной точки М к старым имеет вид В матричном виде эти равенства можно записать в виде где матрица перехода

Найдем обратное преобразование системы координат, найдем матрицу 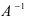обратную к матрице А:

Найдем алгебраические дополнения всех элементов

Запишем обратную матрицу

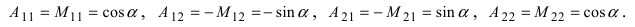
Определение: Унитарными преобразованиями называются такие преобразования, для которых определитель матрицы преобразования равен 1.

Определение: Ортогональными преобразованиями называются такие преобразования, для которых обратная матрица к матрице преобразования совпадает с транспонированной матрицей преобразования.

Таким образом, имеем 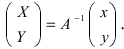Следовательно, формулы перехода от старой системы отсчета к новой системе отсчета имеют вид:

Пример:

Найти координаты точки М(1; 2) в новой системе координат, повернутой относительно старой системы отсчета на угол

Решение:

Воспользуемся полученными формулами 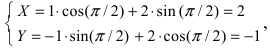т.е. в новой системе координат точка имеет координаты М(2; -1).

Рассмотрим применение преобразования координат:

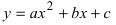
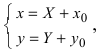
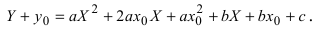
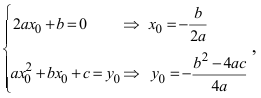
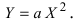
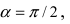
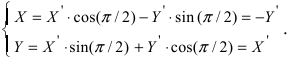
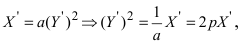
а) Преобразовать уравнение параболы к каноническому виду. Проведем параллельный перенос системы координат получим Выберем начало отсчета новой системы координат так, чтобы выполнялись равенства тогда уравнение принимает вид Выполним поворот системы координат на угол тогда Подставим найденные соотношения в уравнение параболы где параметр параболы

Пример:

Преобразовать уравнение параболы 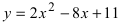к каноническому виду.

Решение:

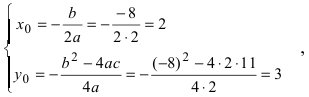
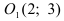
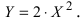
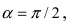
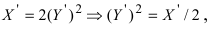
Найдем начало отсчета новой системы координат после параллельного переноса т.е. точка — начало координат новой системы отсчета. В этой системе уравнение параболы имеет вид Проведем поворот системы отсчета на угол тогда

следовательно, параметр параболы р = 1/4.

б) Выяснить, какую кривую описывает функция

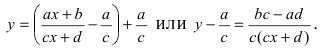
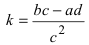
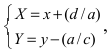
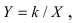
Проведем следующее преобразование Производя параллельный перенос системы координат, вводя обозначение

и новые координаты получим уравнение которое описывает равнобочную гиперболу.

Полярные координаты. Замечательные кривые

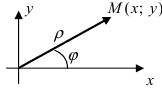
Пусть полярная ось совпадает с осью абсцисс Ох, а начало полярной оси (полюс полярной системы координат) совпадает с началом координат декартовой системы отсчета (Рис. 48). Любая точка М(х;у) в полярной системе координат характеризуется длиной радиус-вектора, соединяющего эту точку с началом отсчета и углом 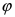между радиус-вектором и полярной осью (угол отсчитывается против часовой стрелки).

Рис. 48. Полярная система координат.

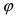
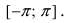
Главными значениями угла являются значения, лежащие в интервале Из рисунка видно, что декартовы и полярные координаты связаны формулами

Рассмотрим замечательные кривые в полярной системе координат:

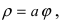
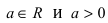
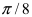
1. Спираль Архимеда где число (Рис. 49). Для построения кривой в полярной системе координат, разобьем декартову плоскость лучами с шагом по углу и на каждом луче отложим ему соответствующее значение р.

Рис. 49. Спираль (улитка) Архимеда.

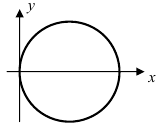
2. Уравнение окружности: уравнение 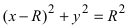описывает окружность с центром в точке A(R; 0) и радиусом R (Рис. 50). В полярной системе координат уравнение принимает вид

Рис. 50. Окружность с центром в точке A(R; 0) и радиусом R.

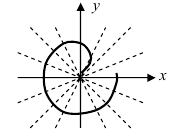
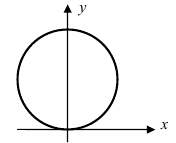
3. Уравнение 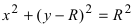описывает окружность с центром в т. А(0; R) и радиусом R (Рис. 51). В полярной системе координат уравнение принимает вид

Рис. 51. Окружность с центром в точке А(0; R) и радиусом R.

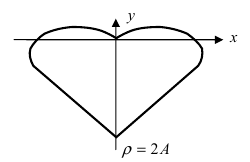
4. Кардиоиды:

Рис. 52. Кардиоида

Рис. 53. Кардиоида

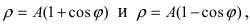
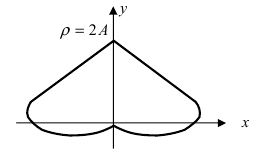
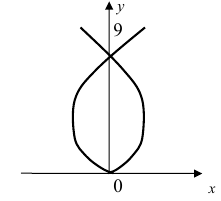
Аналогично выглядят кардиоиды но они вытянуты вдоль оси абсцисс Ох.

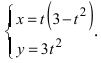
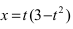
5. Петля: Величина равна нулю при

Для первого корня у = 0, а для второго и третьего — у = 9 . Следовательно, петля имеет вид

Рекомендую подробно изучить предметы:

Математика
Алгебра
Линейная алгебра
Векторная алгебра
Высшая математика
Дискретная математика
Математический анализ
Математическая логика

Ещё лекции с примерами решения и объяснением:

Бесконечно малые и бесконечно большие функции
Замечательные пределы
Непрерывность функций и точки разрыва
Точки разрыва и их классификация
Экстремум функции
Методы решения систем линейных алгебраических уравнений (СЛАУ)
Скалярное произведение и его свойства
Векторное и смешанное произведения векторов

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Видео:Полярная система координатСкачать

Примеры решений: кривые второго порядка

В этом разделе вы найдете бесплатные примеры решений задач по аналитической геометрии на плоскости на тему Кривые второго порядка: приведение к каноническому виду, нахождение характеристик, построение графика т.п.

Видео:Семинар №9 "Приведение уравнения второго порядка к каноническому виду"Скачать

Кривые 2-го порядка: решения онлайн

Задача 1. Привести к каноническому виду уравнение кривой 2 порядка, найти все ее параметры, построить кривую.

Задача 2. Дана кривая. Привести к каноническому виду. Построить и определить вид кривой.

Задача 3. Выяснить вид кривой по общему уравнению, найти её параметры и положение в системе координат. Сделать рисунок.

Задача 4. Общее уравнение кривой второго порядка привести к каноническому. Найти координаты центра, координаты вершин и фокусов. Написать уравнения асимптот и директрис. Построить линии на графики, отметить точки.

Задача 5. Дана кривая $y^2+6x+6y+15=0$.
1. Докажите, что данная кривая – парабола.
2. Найдите координаты ее вершины.
3. Найдите значения ее параметра $р$.
4. Запишите уравнение ее оси симметрии.
5. Постройте данную параболу.

Задача 6. Дана кривая $5x^2+5y^2+6xy-16x-16y=16$.
1. Докажите, что эта кривая – эллипс.
2. Найдите координаты центра его симметрии.
3. Найдите его большую и малую полуоси.
4. Запишите уравнение фокальной оси.
5. Постройте данную кривую.

Задача 7. Найти уравнения параболы и её директрисы, если известно, что парабола имеет вершину в начале координат и симметрична относительно оси $Ox$ и что точка пересечения прямых $y=x$ и $x+y-2=0$ лежит на параболе.

Задача 8. Составить уравнение кривой, для каждой точки которой отношение расстояния до точки $F(0;10)$ к расстоянию до прямой $x=-4$ равно $sqrt$. Привести это уравнение к каноническому виду и определить тип кривой.

Задача 9. Даны уравнения асимптот гиперболы $y=pm 5x/12$ и координаты точки $M(24,5)$, лежащей на гиперболе. Составить уравнение гиперболы.

Задача 10. Даны уравнение параболы $y=1/4 x^2+1$ и точка $C(0;2)$, которая является центром окружности. Радиус окружности $r=5$.
Требуется найти
1) точки пересечения параболы с окружностью
2) составить уравнение касательной и нормали к параболе в точках её пересечения с окружностью
3) найти острые углы, образуемые кривыми в точках пересечения. Чертёж.