Кривая усталости и ее уравнения (8 видео)

Уравнение кривой многоцикловой усталости. Прогнозирование усталостных разрушений

В результате многочисленных экспериментальных и теоретических исследований [21, 22, 33, 72, 73, 74, 82, 93, 95, 124, 127, 130, 133, 140, 147, 161, 162, 186, 188, 205, 207, 211] получено несколько уравнений кривой усталости. Так как механические характеристики металлов и деталей носят вероятностный характер, то наиболее часто кривую многоцикловой усталости описывают степенным уравнением с экспериментальными параметрами

(2.129)

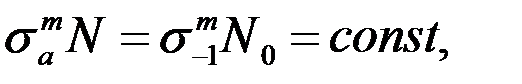
где N₀ — базовое число циклов при пределе выносливости (или s_-1); N — разрушающее число циклов при амплитуде s_a, m — экспериментальный параметр, характеризующий крутизну кривой усталости.

Уравнение (2.129) не предусматривает ассимптоты на уровне предела выносливости. Для описания кривой усталости с переломом на уровне предела выносливости К. Штромейстером [161] предложено уравнение с тремя параметрами

(2.130)

где b — также экспериментальный параметр.

В дальнейшем в результате обобщения степенного уравнения кривой усталости В. Вейбуллом [211] было предложено четырехпараметрическое уравнение

(2.131)

где b, В, m— экспериментальные статистические параметры.

Общее уравнение кривой усталости, как малоцикловой, так и многоцикловой получено С. Мэнсоном [161], которое записывается для деформаций в виде

(2.132)

где — полная деформация; — пластическая деформация; — упругая деформация; е_Т — деформация, соответствующая пределу текучести s_т; j — характеристика пластичности металла ( — первоначальная площадь поперечного сечения образца; F_k — конечная площадь при разрушении); N — разрушающее число циклов; s_b — предел прочности; Е — модуль упругости; m, s — экспериментальные параметры, которые обычно для конструкционных сталей равны [161] m = 0,5. 0,6 и s = 0,10. 0,12.

Так как второй член уравнения (2.132) мало зависит от числа циклов, он может быть заменен постоянным членом , равным размаху упругой деформации на уровне предела выносливости s_-1 (с учетом того, что уравнение кривой усталости при N®¥ имеет ассимптоту). В относительных условных амплитудах напряжений уравнение (2.132) по предложению Б. Лангера [161] примет вид

(2.133)

где — амплитуда напряжений, отнесенная к пределу текучести ; — предел выносливости, отнесенный к пределу текучести ( ).

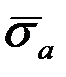
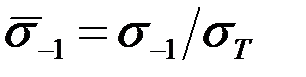
При снижении уровня переменных напряжений снижается доля пластической деформации в полной деформации и, как видно из уравнения (2.133), преимущественное значение приобретает второй член, характеризующий зависимость числа циклов до разрушения от амплитуды упругой деформации

(2.134)

Накопление усталостных повреждений в деталях при малоцикловой усталости объясняется постепенным накоплением пластических деформаций из-за превышения предела текучести s_Т [161] (рис. 2.90, а).

Рис. 2.90. Образование гистерезиса в области малоцикловой (а) и многоцикловой (б) усталости (е_п — накопленная пластическая деформация за первый цикл нагружения)

В области многоцикловой усталости, то есть при упругих деформациях проявляются отклонения от абсолютной упругости и наблюдается гистерезис (рис. 2.90, б), обусловленный микропластическими деформациями [161] (подобный тому, что и при малоцикловой усталости).

При малоцикловой усталости накопленная пластическая деформация е_п за первый цикл нагружения обусловлена снижением предела текучести после разгрузки , что называется эффектом Баушингера [161]. Появление микропластических деформаций при многоцикловой усталости обусловлено неоднородностью строения материала деталей, которая была охарактеризована В.Л. Кирпичевым [161]. На основе существования пластически деформированных элементов материала при общей упругой деформации Е. Орованом была предложена модель процесса деформации и разрушения микропластических элементов за счет гистерезиса как и при малоцикловой усталости.

Видео:Видеоурок "Нормальное уравнение прямой"Скачать

В результате анализа этой модели получено уравнение кривой многоцикловой усталости [161]

(2.110)

где s_ае — часть амплитуды напряжений, вызывающая лишь упругие деформации; s_р — разрушающие напряжения для пластического элемента (s_р близок к s_-1); A— экспериментальный параметр.

Большинство параметров приведенных зависимостей носят вероятностный характер [161], а зависимости в основном используются при расчете деталей машин. Для описания процесса накопления усталостных повреждений в деталях в процессе эксплуатации целесообразно использовать более простые зависимости (с меньшим числом параметров), но отражающие физический смысл усталостного разрушения. Это еще обусловлено и значительной вариацией нагрузочных режимов деталей в различных условиях эксплуатации.

Теоретически и экспериментально установлена зависимость между амплитудой напряжений σ и числом циклов N нагружения до разрушения

где: σ_i – текущая амплитуда напряжений; т – угловой коэффициент кривой усталости; N_i – текущее число циклов; σ_r – предел выносливости; N_r – число циклов, соответствующее пределу выносливости.

Логарифмированием эту зависимость можно представить в линейном виде.

где т – угловой коэффициент, равный по величине тангенсу угла наклона кривой усталости, т = tg ψ (рис.2.91); А = lgN_R+mlgσ_r

По этой зависимости можно прогнозировать число циклов N_i до разрушения детали, работающей при амплитуде напряжений σ_i. Однако деталь не работает при постоянной амплитуде напряжений. Она может сделать n₁ циклов при напряжении σ₁, n₂ при σ₂,…, n_i при σ_i. Если бы деталь все время работала при напряжении σ₁, то она проработала бы до разрушения N₁ циклов, а поскольку она работала при напряжении σ₁ только n₁ циклов, то у нее использована только n₁/ N₁ часть ресурса.

Рис. 2.91. Кривая усталости в логарифмических координатах

Согласно гипотезе накопления усталостных повреждений, чтобы деталь не разрушилась ранее усталостного срока, необходимо соблюдать условие

(2.113)

Экспериментально установлено, что общая сумма долей работы детали при определенном напряжении больше единицы

(2.114)

где а – зависит от материала детали и условий нагружения.

Если известны число циклов нагружения и соответствующие напряжения, величина параметра а, то можно определить оставшиеся число циклов n_к при напряжении σ_к до разрушения детали

(2.115)

Таким образом, при наличии данных о распределении нагрузок и соответствующих пробегов можно прогнозировать с некоторой вероятностью пробег до отказа в результате постепенного необратимого накопления повреждений, определить режим работы без образования субмикротрещин.

Видео:Уравнение, которое меняет взгляд на мир [Veritasium]Скачать

Основные закономерности развития усталостных разрушений в процессе эксплуатации могут быть получены на основе кривой многоцикловой усталости. Основой для аналитического описания кривой многоцикловой усталости деталей можно считать структурную неоднородность материала и модель Е. Орована [161] процесса микропластического деформирования и разрушения пластических элементов материала при переменном нагружении. При определенном условиями эксплуатации среднем уровне амплитуды напряжений в детали s_а, в процессе эксплуатации, то есть с возрастанием числа циклов нагружения N, в материале детали постепенно возрастает число разрушенных пластических элементов. В результате этого сокращается число несущих упруго-деформируемых элементов.

Это можно пояснить графически (рис. 2.92) с учетом фактической неоднородности и диаграмм нагружения и деформации различных элементов детали, имеющих и различный уровень предела текучести, закон распределения которого можно принять нормальным. По мере разрушения пластических элементов с возрастанием числа циклов нагружения сокращается число несущих упруго деформируемых элементов (не заштрихованная площадь под кривой распределения на рис. 2.92), а фактическая амплитуда напряжений в упруго деформируемых элементах s_аф возрастает, что приводит и к превышению среднего предела текучести 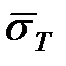и предела прочности. Оставшееся сечение детали при этом уже подвергается хрупкому разрушению (происходит долом детали).

Рис. 2.92. Схема влияния структурной неоднородности материала детали на рост фактической амплитуды напряжений s_аф с увеличением числа циклов нагружения: а — семейство диаграмм нагружения и деформации элементов материала; б — распределение предела текучести и рост s_аф в процессе циклического нагружения

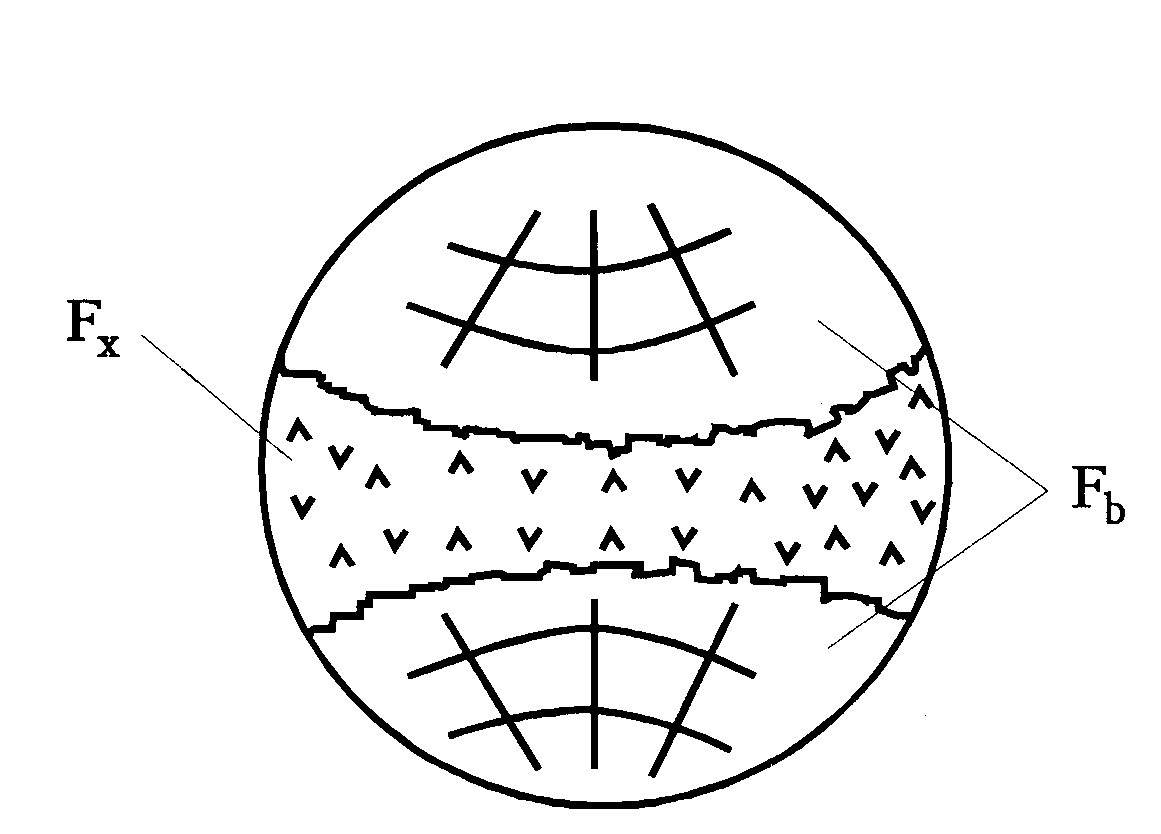
В результате распространения усталостных трещин вглубь детали сечение разрушения имеет две характерные области (рис. 2.93). В области вязкого (пластического) разрушения F_в поверхность гладкая (зеркальная), так как в процессе деформации микронеровности (зерна) взаимно приглаживаются. В области хрупкого разрушения «долома» F_x поверхность имеет матовую зернистую структуру

F_х

F_в

Рис. 2.93. Схема поверхности усталостного разрушения при симметричном изгибе — а и кручении — б (F_в — область вязкого, F_x — хрупкого разрушения)

Форма и соотношение площадей, занятых усталостной областью и окончательным изломом зависят от формы сечения элемента, способа его циклического нагружения, наличия концентраций напряжений и от влияния среды. Для круглого сечения при знакопеременном изгибе в одной плоскости (близкий к симметричному) при более высоких циклических напряжениях трещина распространяется с двух сторон (рис. 2.94, а).

При более низких напряжениях и ассиметричном нагружении встречная трещина от точки А₂ запаздывает и излом несимметричный с меньшей, чем в первом случае зоной домлома (рис. 2.94, б). Типы изломов в и г свойственны вращающемуся круглому элементу при изгибе в одной плоскости (в – более высокие напряжения г – более низкие циклические напряжения). Типы изломов д и е соответствуют предыдущим условиям нагружения при наличии концентрации напряжений в круглом элементе, например от галтели или выточки (д – боле высокие напряжения, трещина развивается от точки А; е – более низкие напряжения).

Рис. 2.94. Форма усталостных изломов элементов круглого сечения: а и б – при изгибе в одной плоскости (а – высокие циклические напряжения, симметричный двухсторонний рост трещин; б – низкие напряжения при ассиметричном изгибе с запаздыванием встречной трещины от точки А₂); в и г – односторонний (пульсирующий) изгиб(в – высокие напряжения; г – низкие напряжения, большая часть излома занята усталостной трещиной, начавшейся в точке А); д и г – изгиб при вращении и наличии концентратора напряжений (д – высокие напряжения; е — более низкие напряжения).

ДоляF_в вязкой части излома (как характеристика степени вязкости разрушения наряду с е_ma_х) наиболее чувствительна к изменению характера разрушения с понижением температуры.

Температура резкого уменьшения F_ви начала уменьшения ψ (рис. 2.95) и е_ma_х характеризуется как температура перехода от вязкого к квазихрупкому состоянию, то есть состоянию при котором поверхность разрушения становится кристаллической. Резко уменьшается пластичность, а разрушающие напряжения остаются выше предела текучести σ_Т.

Температура такого перехода характеризуется как первая критическая температура перехода t_кр1. При второй критической температуре t_кр2: σ_к = σ_Т. Это температура перехода от квазихрупкого состояния к хрупкому. Значения критических температур заметно повышаются с увеличением размеров сечений: при росте площади сечения на три порядка (от маленького образца до крупногабаритных деталей) прирост составляет 100-120 0 С, для малоуглеродистых сталей, достигают положительных значений температуры. Температурный запас вязкости h_t по Н.М. Давиденкову определяют из соотношения [161]

где t_э – минимальная температура металла в условиях эксплуатации, 0 К; t_кр – первая критическая температура, 0 К.

Рис. 2.95. Влияние снижения температуры на механические и усталостные характеристики металла

Для математического описания процесса усталостного разрушения, то есть изменения фактической амплитуды напряжений s_аф и площади разрушения F_р с ростом числа циклов нагружения N необходимо рассмотреть некоторые соотношения и допущения. В качестве первого допущения считаем, что интенсивность разрушения a_F возрастает прямо пропорционально фактической амплитуде действующих напряжений s_аф, то есть

(2.117)

где a— коэффициент пропорциональности, характеризующий изменение a_f на единицу амплитуды напряжений .

Это первое допущение можно объяснить законом Гука, по которому в пределах упругости деформация (приводящая к микропластическим разрушениям) прямо пропорциональна величине приложенных напряжений.

Видео:Повторяем решение уравнений. Полезно всем! Вебинар | МатематикаСкачать

Зависимость s_аф от F_p, как второе допущение, можно принять линейной в виде

, (2.118)

где ; с — коэффициент пропорциональности, характеризующий изменение амплитуды напряжения на единицу площади разрушения ( ).

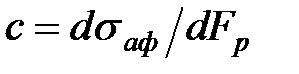
Величина применяется в качестве свободного члена вследствие того, что усталостные разрушения начинают развиваться только при условии s_a>s_-1, то есть при превышении амплитуды предела усталости. С учетом зависимости (2.118) дифференциальное уравнение (2.117) примет вид

. (2.119)

Интегрирование дифференциального уравнения (2.119) при начальных условиях F_p=0 при N=0 позволяет получить зависимость площади разрушения F_p от числа циклов N в виде

или , (2.120)

где b=ас — коэффициент, с учетом смысла, параметров а и с имеет размерность, обратную N, — характеризует интенсивность разрушения в начале эксплуатации, обусловленную наличием концентраторов напряжений на поверхности детали (шероховатость, микротрещины от обработки и др.), неоднородностью материала, имеет размерность площади.

С учетом зависимостей (2.118) и (2.120) получим зависимость фактической амплитуды напряжений s_аф от числа циклов нагружения

(2.121)

То есть, в процессе эксплуатации фактическая амплитуда напряжений в несущих элементах материала детали возрастает по экспоненциальной зависимости (2.121). Разрушение детали произойдет тогда (при N=N_k), когда s_аф достигнет предела прочности s_в для оставшихся несущих элементов, то есть с учетом зависимости (2.121)

(2.122)

Отсюда вытекает аналитическое выражение кривой многоцикловой усталости

(2.123)

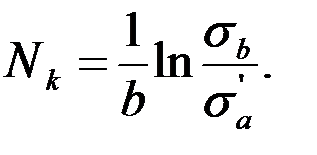
Графическое пояснение развития разрушения в процессе эксплуатации по зависимости (2.121) и построение кривой многоцикловой усталости по условию (2.122) приведено на рис. 2.96, где показано семейство кривых (2.121) при различных уровнях s_а. Здесь также показано влияние исходного уровня амплитуды напряжений s_а на величину площади хрупкого разрушения F_x. Видно, что по мере роста s_а площадь F_x (заштрихованная) увеличивается.

Рис. 2.96. Повышение фактической амплитуды напряжений s_аф в процессе эксплуатации при различных, уровнях исходной амплитуды s_а и схема образования кривой усталости

Для сложившихся условий эксплуатации автомобиля можно считать, что в единицу времени или за единицу пробега деталь испытывает определенное число циклов нагружения. Следовательно, зависимости (2.121) и (2.123) справедливы и для таких измерителей процесса эксплуатации, как время t и пробег l вместо N, то есть

(2.124)

(2.125)

В этом случае значения параметра b, будут другими, чем в зависимостях (2.121) и (2.123).

Наиболее часто в автомобиле усталостным разрушениям подвержены такие детали, как рессоры, поворотные кулаки, полуоси, пружины подвески, зубчатые передачи, подшипники качения, а также в некоторых случаях рабочая поверхность вкладышей подшипников коленчатого вала. Зачастую после ремонта усталостным разрушениям подвержены и коленчатые валы, особенно восстановленные наплавкой. Как правило, последствия усталостных разрушений тяжелее, чем отказов, обусловленных изнашиванием, так как их редко контролируют в процессе эксплуатации, вследствие чего их часто относят к разряду «внезапных» отказов. Для прогнозирования усталостных разрушений деталей необходимо, кроме закономерностей их развития в процессе эксплуатации, иметь и численные измерители, позволяющие оценить степень усталостных разрушений, их предельные значения и зависимости от наработки (тип зависимости и параметры).

Показателями усталостного разрушения таких деталей, как рессоры, поворотные кулаки, полуоси и подобные, могут быть концентрация микротрещин, их глубина, длина и пропорциональная им площадь разрушения. В настоящее время существуют методы и средства контроля (диагностирования) этих показателей усталостного разрушения [82, 139, 140, 147]. В качестве оценочного показателя (измерителя) для таких деталей, как рессоры в работе [140], предложено отношение поврежденной площади сечения F_n к номинальной площади сечения F_n (D=F_n/F_н).

Данный критерий является безразмерным и удобным для прогнозирования. Однако несколько затруднено определение номинальной площади F_n, так как в процессе эксплуатации возникает и развивается, как правило, множество усталостных трещин, суммарная площадь которых может превышать номинальную площадь сечения детали (например, рессоры) и критерий D может быть больше единицы, что снижает его информационную ценность. Кроме того, трещины в деталях зачастую распространяются не перпендикулярно поверхности детали, а под некоторым углом и по сложной криволинейной поверхности.

Для таких деталей, как зубчатые колеса, беговые дорожки подшипников качения, вкладыши подшипников усталостные разрушения чаще всего проявляются в виде выкрашивания рабочей поверхности — питтинга. Количество выкрошенного материала можно оценить по площади, занимаемой лунками (оспинками), отнесенной к площади всей рабочей поверхности [46, 50, 52], что аналогично критерию D, который в этом случае меньше единицы.

Видео:5. Нормальное уравнение плоскости выводСкачать

Все показатели усталостного разрушения деталей (длина трещины, их глубина, концентрация микротрещин, площадь выкрашивания и др.) прямо пропорциональны площади разрушения и с ростом числа циклов нагружения возрастают по экспоненциальной зависимости (2.120), аналогично и с ростом наработки t или l.

Следует отметить, что зависимость (2.120) получена для периода эксплуатации после приработки. В начале периода приработки величина напряжений и их амплитуды более высокая, чем в конце вследствие технологических отклонений. Эта величина может с большей вероятностью превышать предел текучести, что приводит к начальным разрушениям в области малоцикловой усталости. В результате в конце периода приработки в детали накапливается площадь разрушения F_p₀. С учетом зависимости (2.120) общая площадь разрушений составит

(2.126)

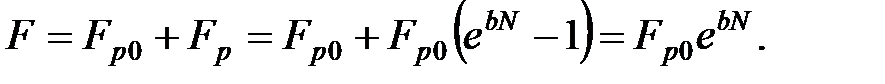
Приведенные аналитические зависимости подтверждаются многочисленными экспериментальными и статистическими данными, результаты математической обработки которых приведены на рис. 2.97 – 2.101. Математическая обработка данных [82] по влиянию амплитуды на интенсивность усталостного разрушения (рис. 2.87) также хорошо подтверждает справедливость допущения (2.117) о прямолинейности этого влияния с высоким коэффициентом корреляции (рис. 2.87).Следует отметить, что степень усталостного разрушения при отказе детали зависит от вида нагружения и от типа деталей.

Характерным отличием развития степени усталостных разрушений деталей является большее рассеивание по сравнению с закономерностями изнашивания и изменения геометрической формы в процессе эксплуатации. Следовательно, прогнозирование и предупреждение усталостных разрушений деталей даже с использованием диагностических средств более сложно, чем износных отказов.

Рис. 2.97. Зависимость длины усталостной трещины в стальном образце от числа циклов нагружения при амплитуде нагрузки (кН): 1 — 18,1; 2 -22,7; 3- 31,8; 4 — 45,5 [82 по данным В. Кларка]

Рис. 2.98. Зависимость интенсивности усталостного разрушения от амплитуды нагрузки (по результатам обработки данных В.Кларка [82])

Рис. 2.99. Зависимость степени разрушения D от доли выработанного ресурса N_T/N цапфы передней оси (1) и коренного листа рессоры (2) автомобиля [140]

Рис. 2.100. Зависимость площади усталостного выкрашивания антифрикционного слоя вкладышей от наработки двигателей ЗИЛ-130 (1) и ЯМЗ-238 (2).

Рис. 2.101. Зависимость площади усталостного выкрашивания рабочей поверхности зубьев ведущей шестерни главной передачи от наработки автомобилей ЗИЛ-130 [52]

Другой отличительной особенностью усталостных разрушений (повреждений) деталей является их меньшая пригодность к восстановлению. Как правило, детали, имеющие усталостные трещины, не подлежат восстановлению и отбраковываются.

Одной из наиболее дорогостоящих деталей автомобиля, подвергающейся циклическим нагрузкам и усталостным повреждениям является коленчатый вал двигателя. Оценить степень усталостных повреждений коленчатого вала можно по количеству (концентрации) усталостных трещин на шейках и галтелях.

При работе коленчатый вал подвергается действию радиальных и тангенциальных составляющих сил, приложенных к его шатунным шейкам, центробежных сил вращающихся масс, реакций опор, а также момента сопротивления вращению трансмиссии. Периодическое действие указанных нагрузок вызывает появление упругих колебаний коленчатого вала (изгибных и крутильных).

Особенно высокие нагрузки несут шатунные шейки и щеки коленчатого вала. Характер разрушений элементов коленчатого вала показывает на преимущественное действие изгибающих моментов и меньшее действие крутящего момента (рис. 2.102 – 2.104). Усталостные разрушения (трещины) начинаются в области концентраторов напряжений (галтели, отверстия для смазки, грязеуловители).

Рис. 2.102. Форма усталостного разрушения коленчатого вала по щеке

Рис. 2.103. Внешний вид продольно-радиальной трещины на шатунной шейке и вид излома по трещине

Рис. 2.104. Увеличенная глубина закалки в зоне трещины и обезуглероженный слой глубиной до 0,1мм

Нарастание степени усталостных разрушений в элементах коленчатого вала в процессе эксплуатации носит стохастический характер. Детерминирующая составляющая этого стохастического процесса может быть обоснована с учетом аналитического описания кривой многоцикловой усталости. Наиболее часто усталостное разрушение вала происходит по щеке в зоне перекрытия шатунных шеек (рис. 2.105, 2.106), которое для двигателей КамАЗ-740 составляет 27,5 мм при номинальном размере шеек. Напряжения изгиба в щеке при этом составят

, (2.127)

где М_и – изгибающий момент (в процессе эксплуатации практически не меняется); W – момент сопротивления сечения на изгиб.

, (2.128)

где J – момент инерции сечения перекрытия (рис. 2.105)

, (2.129)

где S_щ – ширина щеки; S_п – минимальное расстояние между галтелями шеек (рис. 2.105).

Видео:3. Частные случаи общего уравнения плоскости Неполные уравнения плоскостиСкачать

Рис. 2.105. Схема опасного сечения щеки и его изменение при перешлифовывании шеек

При перешлифовывании коренных и шатунных шеек на последний ремонтный размер перекрытие сокращается на 2 мм (7,2%). Расчеты по формулам (2.127, 2.128) показывают, что уровень напряжений изгиба повышается при этом в среднем на 8%. Более существенно снижается несущее сечение в процессе эксплуатации за счет распространения усталостных трещин от очагов (в данном случае галтелей), что показано на рис. 2.105 и 2.106.

Рис. 2.106. Схема развития усталостных трещин в опасном сечении

щеки от очагов на галтелях

Основным дефектом остаются трещины шатунной шейки. Внешний вид трещины показан на рис. 2.103. Фокус разрушения расположен в зоне галтели. Продольно-радиальная трещина образовывается при объемной закалке. Глубина распространения трещины находится в пределах 15÷20 мм. В зоне трещины наблюдается увеличение глубины закаленного слоя на 1 мм – рис. 2.104. Там же показан обезуглероженный слой в конце радиальной трещины.

Собранные статистические данные по количеству усталостных трещин и их средней длине на коленчатых валах двигателей КамАЗ-740 и ЯМЗ-238 в зависимости от наработки (всего проанализировано около 450 коленчатых валов) подтверждают экспоненциальный характер степени усталостного разрушения коленчатых валов (рис. 2.107, 2.108).

Рис. 2.107. Зависимость количества усталостных трещин на коленчатом вале двигателей КамАЗ-740 — 1 и ЯМЗ-238 — 2 от наработки

Рис. 2.108. Зависимость средней длины усталостной трещины

на коленчатом вале двигателей КамАЗ-740 — 1

и ЯМЗ-238 — 2 от наработки

В процессе анализа технического состояния двигателей КамАЗ-740 и ЯМЗ-238, поступивших в капитальный и текущий ремонт определяли также количество поломанных коленчатых валов. Как показывает анализ поверхностей разрушения (рис. 2.102), на ней можно выделить гладкий участок (распространение трещины) и зернистый участок (хрупкий долом). Это свидетельствует об усталостном характере разрушения коленчатого вала. Количество поломанных валов увеличивается с ростом наработки также по экспоненциальной зависимости (рис. 2.109).

Рис. 2.109. Зависимость доли поломанных коленчатых валов

двигателей КамАЗ-740 — 1 и ЯМЗ-238 — 2 от наработки

Видео:13. Общие уравнения прямой в пространстве / приведение к каноническому видуСкачать

Приведенные на рис. 2.107 – 2.109 данные свидетельствуют также о значительном влиянии материала коленчатого вала и условий работы на интенсивность усталостного разрушения. Коленчатый вал двигателей ЯМЗ-238 изготовлен из марганцевой стали 50Г, имеющей хорошие усталостные характеристики. Коленчатый вал двигателей КамАЗ-740 изготовлен из штамповой стали 42ХМФА-Ш, которая имеет склонность к трещинообразованию при хорошей износостойкости.

Кроме того, номинальная частота вращения коленчатого вала двигателей ЯМЗ-238 составляет 2100 мин -1 , а КамАЗ-740 — 2600 мин -1 , что существенно повышает уровень амплитуды циклических нагрузок у последних. Давление в системе смазки двигателей ЯМЗ-238 в среднем в 1,6 раза выше, чем у двигателей КамАЗ-740, что также повышает вероятность контакта шеек и вкладышей и контактные нагрузки.

Все эти факторы обуславливают большую интенсивность усталостных разрушений коленчатых валов двигателей КамАЗ-740, чем ЯМЗ-238 от 2-х до 4-х раз. В результате к наработке коленчатого вала двигателя КамАЗ-740 около 200 тыс. км, средняя длина трещин достигает предельных значений 4 мм (рис. 2.108), при которых обычно вал ремонтируют. Перешлифовывание их под очередной ремонтный размер лишь в половине случаев устраняет эти трещины. К этой же наработке количество поломанных коленчатых валов достигает 4% (рис. 2.109). Даже при восстановлении этих коленчатых валов наплавкой при дефектовке отбраковывается более половины ремфонда с наработкой более 200 тыс. км. Усталостная прочность восстановленных наплавкой коленчатых валов двигателей КамАЗ-740 еще ниже, чем не восстановленных, так как в элементах вала уже накоплены значительные усталостные разрушения, которые не всегда возможно обнаружить при дефектовке (внутренние трещины). Усталостная долговечность таких валов даже при высоком качестве восстановления не превышает 60-80 тыс. км.

Таким образом, в процессе эксплуатации автомобиля под действием циклических нагрузок происходит усталостное разрушение деталей. Разрушение может проявляться в виде образования сетки растрескивания, магистральных трещин деталей, выкрашивания поверхности трения (питтинг). Эти показатели, характеризующие степень усталостного разрушения деталей в процессе эксплуатации, возрастают по экспоненциальной зависимости (2.126). При выборе сроков и способов ремонта и восстановления деталей необходимо использовать методы и средств диагностирования и деффектовки для прогнозирования их ресурса, как первичного, так и вторичного.

источники: