Кривая проходит через точку найти уравнение кривой

Содержание:

Геометрической фигурой или просто фигурой на плоскости называется множество точек. Задать фигуру — значит указать, из каких точек плоскости она состоит. Одним из важных способов задания фигуры на плоскости является ее задание при помощи уравнений с двумя неизвестными. Произвольное уравнение с двумя неизвестными х и у записывается в виде

1. Если точка М(а,Ь) принадлежит фигуре Ф, то координаты (а,Ь) являются решениями уравнения
2. если пара чисел (c,d) является решением уравнения F(x,y) = 0, то точка N(c,d) принадлежит фигуре Ф.

Это определение в более компактной записи выглядит следующим образом. Уравнение называется уравнением фигуры, если , то есть (а, b) — решение уравнения F(x,y) = 0.

Из определения уравнения фигуры следует, что фигура Ф состоит только из тех точек плоскости, координаты которых являются решениями уравнения , т.е. уравнение фигуры задает эту фигуру.

Возможны два вида задач:

1. дано уравнение и надо построить фигуру Ф, уравнением которой является ;
2. дана фигура Ф и надо найти уравнение этой фигуры.

Первая задача сводится к построению графика уравнения и решается, чаще всего, методами математического анализа.

Для решения второй задачи, как следует из определения уравнения фигуры, достаточно:

1. Задать фигуру геометрически, т.е. сформулировать условие, которому удовлетворяют только точки фигуры (довольно часто определение фигуры содержит такое условие);
2. Записать в координатах условие, сформулированное в первом пункте.

Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Эллипс

Эллипсом называется линия, состоящая из всех точек плоскости, для каждой из которых сумма расстояний до двух данных точек , есть величина постоянная (большая, чем расстояние между ).

Точки называются фокусами эллипса. Обозначив расстояние между фокусами через 2с, а сумму расстояний от точек эллипса до фокусов через 2а, имеем с b. В этом случае а называется большой полуосью, a b — малой.

Если а =Ь, то уравнение (7.3) можно переписать в виде:

(7.5)

Это уравнение окружности с центром в начале координат. Эллипс (3) можно получить из окружности (4) сжатием плоскости к оси Ох. Пусть на плоскости выбрана прямоугольная система координат Оху. Тогда преобразование, переводящее произвольную точку М(х,у) в точку координаты которой задаются формулами будет окружность (4) переводить в эллипс, заданный соотношением

Число называется эксцентриситетом эллипса. Эксцентриситет характеризует форму эллипса: чем ближе к нулю, тем больше эллипс похож на окружность; при увеличении становится более вытянутым

Фокальными радиусами точки М эллипса называются отрезки прямых, соединяющие эту точку с фокусами . Их длины и задаются формулами Прямые называются директрисами эллипса. Директриса называется левой, а — правой. Так как для эллипса и, следовательно, левая директриса располагается левее левой вершины эллипса, а правая — правее правой вершины.

Директрисы обладают следующим свойством: отношение расстояния г любой точки эллипса от фокуса к ее расстоянию d до соответствующей директрисы есть величина постоянная, равная эксцентриситету, т.е.

Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Гипербола

Гиперболой называется линия, состоящая из всех точек плоскости, модуль разности расстояний от которых до двух данных точек есть величина постоянная (не равная нулю и меньшая, чем расстояние между ).

Точки называются фокусами гиперболы. Пусть по-прежнему расстояние между фокусами равно 2с. Модуль расстояний от точек гиперболы до фокусов обозначим через а. По условию, а 0) (рис. 9.7). Ось абсцисс проведём через фокус F перпендикулярно директрисе. Начало координат расположим посередине между фокусом и директрисой. Пусть А — произвольная точка плоскости с координатами (х, у) и пусть . Тогда точка А будет лежать на параболе, если r=d, где d- расстояние от точки А до директрисы. Фокус F имеет координаты .

Тогда А расстояние Подставив в формулу r=d, будем иметь. Возведя обе части равенства в квадрат, получим

или

(9.4.1)

Уравнение (9.4.1)- каноническое уравнение параболы. Уравнения также определяют параболы.

Легко показать, что уравнение , определяет параболу, ось симметрии которой перпендикулярна оси абсцисс; эта парабола будет восходящей, если а > 0 и нисходящей, если а О. Для этого выделим полный квадрат:

и сделаем параллельный перенос по формулам

В новых координатах преобразуемое уравнение примет вид: где р — положительное число, определяется равенством .

Пример:

Пусть заданы точка F и прямая у =-1 (рис. 9.8). Множество точек Р(х, y) для которых расстояние |PF| равно расстоянию, называется параболой. Прямая у = -1 называется директрисой параболы, а точка F — фокусом параболы. Чтобы выяснить, как располагаются точки Р, удовлетворяющие условию, запишем это равенство с помощью координат: , или после упрощения . Это уравнение геометрического места точек, образующих параболу (рис. 9.8).

Видео:Уравнения касательной и нормали к кривой, заданной в неявном видеСкачать

Кривые второго порядка на плоскости

Кривой второго порядка называется фигура на плоскости, задаваемая в прямоугольной системе координат уравнением второй степени относительно переменных х и у:

где коэффициенты А, В и С не равны одновременно нулю

Любая кривая второго порядка на плоскости принадлежит к одному из типов: эллипс, гипербола, парабола, две пересекающиеся прямые, 2 параллельные прямые, прямая, точка, пустое множество.

Кривая второго порядка принадлежит эллиптическому типу, если коэффициент В равен нулю: В=0, а коэффициенты А и С имеют одинаковые знаки: АС>0.

Кривая второго порядка принадлежит гиперболическому типу, если коэффициент В равен нулю: В=0, а коэффициенты А и С имеют противоположные знаки: АС 2с. Точка М(х,у) принадлежит эллипсу тогда и только тогда, когда ее координаты удовлетворяют уравнению

которое называют каноническим уравнением эллипса.

Число а называют большей полуосью эллипса, число — мень-

шей полуосью эллипса, 2а и 2b — соответственно большей и меньшей осями эллипса. Точки называют вершинами эллипса, а — его фокусами (рис. 12).

Координатные оси являются осями симметрии эллипса, а начало координат — его центром симметрии. Центр симметрии эллипса называется центром эллипса.

Замечание. Каноническое уравнение эллипса можно рассматривать и в случае b>а. Оно определяет эллипс с большей полуосью b, фокусы которого лежат на оси Оу.

В случае а=b каноническое уравнение эллипса принимает вид и определяет окружность радиуса а с центром в начале координат.

Эксцентриситетом эллипса называется отношение фокусного расстояния к длине большей оси.

Так, в случае а>b эксцентриситет эллипса выражается формулой:

Эксцентриситет изменяется от нуля до единицы и характеризует форму эллипса. Для окружности Чем больше эксцентриситет, тем более вытянут эллипс.

Пример:

Показать, что уравнение

является уравнением эллипса. Найти его центр, полуоси, вершины, фокусы и эксцентриситет. Построить кривую.

Решение:

Дополняя члены, содержащие х и у соответственно, до полных квадратов, приведем данное уравнение к каноническому виду:

— каноническое уравнение эллипса с центром в точке большей полуосью а=3 и меньшей полуосью

Найдем эксцентриситет эллипса:

Для вычисления вершин и фокусов удобно пользовать новой прямоугольной системой координат, начало которой находится в точке а оси параллельны соответственно осям Ох, Оу и имеют те же направления (осуществили преобразование параллельного переноса). Тогда новые координаты точки будут равны ее старым координатам минус старые координаты нового начала, т.е.

В новой системе координат координаты вершин и фокусов гиперболы будут следующими:

Переходя к старым координатам, получим:

Построим график эллипса.

Задача решена.

Гиперболой называется множество всех точек плоскости, для которых модуль разности расстояний до двух данных точек, называемых фокусами, есть величина постоянная, меньшая расстояния между фокусами.

Так же, как и для эллипса, геометрическое свойство точек гиперболы выразим аналитически. Расстояние между фокусами назовем фокусным расстоянием и обозначим через 2с. Постоянную величину обозначим через 2а: 2а

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Видео:Математика без Ху!ни. Уравнение касательной.Скачать

Геометрические и физические задачи

56. . 57. .

58. .

Проинтегрировать следующие уравнения, для которых интегрирующий множитель или :

59. . 60. .

61. . 62. .

63. .

64. .

65. .

10.4. Геометрические и физические задачи,

Видео:Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать

уравнений первого порядка

1°. Геометрические задачи. В задачах геометрии, в которых требуется найти уравнение кривой по заданному свойству ее касательной, нормали или площади криволинейной трапеции, используются геометрическое истолкование производной – угловой коэффициент касательной – и интеграла с переменным верхним пределом – площадь криволинейной трапеции с подвижной ограничивающей ординатой, а также общие формулы для определения длин отрезков касательной t, нормали n, подкасательной и поднормали :

. (10.39)

Пример 1. Найти уравнение кривой, проходящей через начало координат, если в каждой ее точке подкасательная в k раз меньше поднормали .

Ñ Пусть – уравнение искомой кривой. Используя
выражения подкасательной и поднормали из (10.39), получаем дифференциальное уравнение или . Интегрируя это уравнение и учитывая начальное условие , получаем искомые уравнения: (две прямые). #

Пример 2. Найти уравнение кривой, проходящей через точку (1; 1), если для любого отрезка площадь криволинейной трапеции, ограниченной соответствующей дугой этой кривой, в два раза больше произведения координат точки кривой .

Ñ По условию задачи, . Дифференцируя это ра-венство по x, получаем дифференциальное уравнение , или . Интегрируя его, с учетом начального условия , получаем уравнение искомой кривой: . #

2°. Задачи с физическим содержанием. При составлении дифференциальных уравнений первого порядка в физических задачах используют метод дифференциалов, по которому приближенные соотношения между малыми приращениями величин заменяются соотношениями между их дифференциалами. В конкретных задачах используется тот или иной физический закон (некоторые из них приведены ниже при формулировании условия задачи), а также физическое истолкование производной как скорости протекания физического процесса.

Пример 3. В резервуаре первоначально содержится A кг вещества, растворенного в В литрах воды и вытекает N литров раствора (M > N), причем однородность раствора достигается путем перемешивания. Найти массу вещества в резервуаре через T минут после начала процесса.

Ñ Обозначим через массу вещества в резервуаре через t минут после начала процесса и через – в момент . Заметим, что при , т. е. раствор обедняется.

Пусть– объем смеси в момент . Концентрация вещества в момент t равняется, очевидно, . За бесконечно малый промежуток времени масса вещества изменяется на бесконечно малую величину (так как процесс непрерывен), для которой справедливо приближенное равенство

(10.40)

Заменяя в (10.40) приращения и дифференциалами dx и dt, получаем дифференциальное уравнение – уравнение с разделяющимися переменными. Интегрируя и считая
M > N, запишем общее решение: . Используя начальное условие: , находим частное решение: . Решение задачи получается из него при t = T. #

З а м е ч а н и е. Случай требует отдельного рассмотрения.

Видео:Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

Задачи для самостоятельного решения

66. Найти уравнение кривой, проходящей через точку , если сумма длин ее касательной и подкасательной равна произведению координат точки касания.

67. Найти уравнение кривой, проходящей через точку , если ее подкасательная вдвое больше абсциссы точки касания.

68. Найти уравнение кривой, проходящей через точку , если длина отрезка полуоси абсцисс, отсекаемого ее касательной, равна квадрату абсциссы точки касания.

69. Найти уравнение кривых, у которых длина отрезка нормали постоянна и равна a.

70. Найти уравнения кривых, у которых поднормаль имеет постоянную длину а.

71. Найти уравнение кривой, проходящей через точку (0; 2), если площадь криволинейной трапеции, ограниченной дугой этой кривой, в два раза больше длины соответствующей дуги.

72. Найти уравнение кривой, проходящей через точку (1; 1/2), если для любого отрезка [1; x] площадь криволинейной трапеции, ограниченной соответствующей дугой этой кривой, равна отношению абсциссы x концевой точки к ординате.

73. Найти уравнение кривой, проходящей через точку (0; 3), если подкасательная в любой точке равна сумме абсциссы точки касания и расстояния от начала координат до точки касания (ограничиться рассмотрением случая ).

74. Найти уравнение кривой, проходящей через точку (1; 0), если длина отрезка оси абсцисс, отсекаемого ее нормалью, на 2 ед. больше абсциссы точки касания.

75. Найти уравнение кривой, проходящей через начало координат, если для любого отрезка площадь криволинейной трапеции, ограниченной соответствующей дугой этой кривой, равна кубу ординаты концевой точки дуги.

76. Найти уравнение кривой, проходящей через точку с полярными координатами , если угол между ее касательной и радиус-вектором точки касания есть постоянная величина: .

77. Найти уравнение кривой, проходящей через точку (1; 1), если длина отрезка оси абсцисс, отсекаемого любой ее касательной, равна длине этой касательной.

78. Найти уравнение кривой, проходящей через точку (3; 1), если длина отрезка, отсекаемого любой ее касательной на оси ординат, равна поднормали.

79. Найти уравнение кривой, проходящей через начало координат, если середина отрезка ее нормали от любой точки кривой до оси Ox лежит на параболе .

80. Найти уравнение кривой, проходящей через точку (1; 0), если площадь трапеции, образованной касательной, осью координат и ординатой точки касания, постоянна и равна 3/2.

81. Найти уравнение кривой, проходящей через точку (0; 1), если площадь треугольника, образуемого осью абсцисс, касательной и радиус-вектором точки касания, постоянна и равна 1.

82. Найти уравнение кривой, проходящей через точку (1; 2), если произведение абсциссы точки касания на абсциссу точки пересечения нормали с осью Ox равно удвоенному квадрату расстояния от начала координат до точки касания.

83. Найти уравнение кривой, проходящей через точку с полярными координатами , если площадь сектора, ограниченного этой кривой, полярной осью и переменным полярным радиусом, в шесть раз меньше куба полярного радиуса.

84. Скорость охлаждения тела пропорциональна разности температур тела и окружающей его среды (закон Ньютона). Найти зависимость температуры T от времени t, если тело, нагретое до , градусов, внесено в помещение, температура которого постоянна и равна а градусам.

85. Через сколько времени температура тела, нагретого до
100 °С, понизится до 25 °С, если температура помещения равна 20°С и за первые 10 мин тело охладилось до 60 °С?

86. Замедляющее действие трения на диск, вращающийся в жидкости, пропорционально угловой скорости вращения. Найти зависимость этой угловой скорости от времени, если известно, что диск, начавший вращаться со скоростью 5 об/с, по истечении двух минут вращается со скоростью 3 об/с. Через сколько времени он будет иметь угловую скорость 1 об/мин?

87. Скорость распада радия пропорциональна наличному его количеству. В течение года из каждого грамма радия распадается 0,44 мг. Через сколько лет распадется половина имеющегося количества радия?

88. Скорость истечения воды из сосуда через малое отверстие оп- ределяется формулой , где h – высота уровня воды над отверстием, g – ускорение свободного падения (принять g = 10 м/с2). За какое время вытечет вся вода из цилиндрического бака с диаметром и высотой H = 1,5 м через отверстие в дне диаметром м?

89. Количество света, поглощаемого при прохождении через тонкий слой воды, пропорционально количеству падающего света и толщине слоя. Зная, что при прохождении слоя воды толщиной 2 м поглощается 1/3 первоначального светового потока, найти, какая часть его дойдет до глубины 12 м.

90. Лодка замедляет свое движение под действием сопротивления воды, которое пропорционально скорости лодки. Начальная скорость лодки 1,5 м/с, скорость ее через 4 секунды 1 м/с. Когда скорость уменьшится до 1 см/с? Какой путь пройдет лодка до остановки?

91. Пуля, двигаясь со скоростью км/с, пробивает стену толщиной h = 20 см и вылетает, имея скорость 100 м/с. Полагая силу сопротивления стены пропорциональной квадрату скорости движения пули, найти время прохождения пули через стену.

92. В баке находится 100 л раствора, содержащего 10 кг соли. В бак вливается вода со скоростью 5 л/мин и смесь вытекает из него с той же скоростью. Однородность раствора достигается путем перемешивания. Сколько соли останется в баке через час?

93. Некоторое вещество преобразуется в другое вещество со скоростью, пропорциональной массе непреобразованного вещества. Если масса первого есть 31,4 г по истечении одного часа и 9,7 г по истечении трех часов, то определить: а) массу вещества в начале процесса; б) через сколько времени после начала процесса останется лишь 1 % первоначальной массы исходного вещества?

94. В помещении цеха вместимостью 10800 м3 воздух содержит 0,12 % углекислоты. Вентиляторы доставляют свежий воздух, содержащий 0,04 % углекислоты, со скоростью 1500 м/мин. Предполагая, что углекислота распределяется по помещению равномерно в каждый момент времени, найти объемную долю углекислоты через 10 мин после начала работы вентиляторов.

95. Сила тока i в цепи с сопротивлением R, самоиндукцией L и напряжением u удовлетворяет уравнению . Найти силу тока i в момент времени t, если и i = 0 при t = 0 (L, R, E, w – постоянные).

10.5. Дифференциальные уравнения высших порядков

10.5.1. Основные понятия и определения. Задача Коши

Задачей Коши для дифференциального уравнения (10.2) называется задача определения решения , удовлетворяющего заданным начальным условиям:

. (10.41)

Определение 1. Общим решением уравнения (10.1) или (10.2) называется такая функция , которая при любых допустимых значениях параметров является решением этого уравнения и для любой задачи Коши с условиями (5.1) , определяемые из системы уравнений:

(10.42)

Определение 2. Уравнение

, (10.43)

определяющее общее решение как неявную функцию, называется общим интегралом дифференциального уравнения.

Теорема существования и единственности решения задачи Коши [(10.2); (10.41)]. Если дифференциальное уравнение (10.2) таково, что функция в некоторой области D изменения своих аргументов непрерывна и имеет непрерывные частные производные , то для любой точки существует такой интервал , на котором существует и притом единственное решение этого уравнения, удовлетворяющее начальным условиям (10.41).

Определение 3. Решение уравнения (10.2) называется частным решением, если в каждой точке его сохраняется единственность решения задачи Коши.

З а м е ч а н и е. Если есть общее решение уравнения (10.2) в области D, то всякое решение, содержащееся в этой формуле при конкретных допустимых числовых значениях произвольных постоянных , является частным решением.

Определение 4. Решение уравнения называется особым, если в каждой точке его нарушается единственность решения задачи Коши.

В случае уравнения второго порядка

(10.44)

задача Коши состоит в нахождении решения уравнения (10.44), удовлетворяющего начальным условиям

при . (10.45)

Геометрически это означает, что ищется интегральная кривая, которая проходит через заданную точку и имеет в этой точке заданную касательную, образующую с положительным направлением оси Ox такой угол , что .

Механический смысл задачи Коши заключается в следующем. Запишем уравнение движения материальной точки в проекции на ось Ox:

(10.46)

Здесь t – время, – соответственно координата, проекции скорости и ускорения на ось Ox в момент t; – проекция силы на ось Ox, действующей на точку. Решение (координата x) уравнения (10.46) называется движением точки, определяемое этим уравнением. Задача Коши заключается в определении движения, удовлетворяющего начальным условиям: при , где числа и (начальные данные) есть соответственно начальный момент времени, начальная координата и проекция скорости в (начальный) момент времени .

Пример 1. Показать, что есть общее решение дифференциального уравнения .

Ñ 1. Покажем, что удовлетворяет данному уравнению при любых . Имеем 2. Пусть заданы произвольные начальные условия . Покажем, что постоянные можно подобрать так, что эти начальные условия будут удовлетворены. Составим систему: , из которой однозначно определяются . Таким образом, решение удовлетворяет поставленным начальным условиям. Заметим, что запись означает, что решение задачи записано в форме Коши. #

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

VMath

Инструменты сайта

Основное

Навигация

Информация

Действия

Содержание

Видео:1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать

Касательная, нормальная плоскость, соприкасающаяся плоскость, бинормаль, главная нормаль, репер Френе

Видео:Составляем уравнение прямой по точкамСкачать

Краткие теоретические сведения

Кривая в пространстве

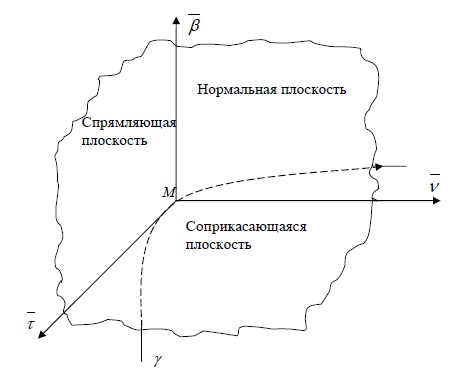
Рассмотрим в пространстве гладкую кривую $gamma$.

Пусть точка $M$ принадлежит данной кривой и отвечает значению параметра $t=t_0$. Тогда радиус-вектор и координаты данной точки равны:

begin vec=vec(t_0), quad x_0=x(t_0),, y_0=y(t_0), , z_0=z(t_0). end

Пусть в точке $M$ $ vec(t_0)neqvec$, то есть $M$ не является особой точкой.

Касательная к кривой

Касательная к кривой, проведенная в точке $M$, имеет направляющий вектор коллинеарный вектору $vec(t_0)$.

Пусть $vec$ — радиус-вектор произвольной точки касательной, тогда уравнение этой касательной имеет вид

Здесь $lambdain(-infty,+infty)$ — параметр, определяющий положение точки на касательной (то есть разным значениям $lambda$ будут соответствовать разные значения $vec$).

Если $vec=$, $M = (x(t_0), y(t_0), z(t_0))$, то можно записать уравнение касательной в каноническом виде:

Нормальная плоскость

Плоскость, проходящую через данную точку $M$ кривой $gamma$ перпендикулярно касательной в этой точке, называют нормальной плоскостью.

Пусть $vec$ — радиус-вектор произвольной точки нормальной плоскости, тогда ее уравнение можно записать в векторном виде через скалярное произведение векторов $vec-vec(t_0)$ и $vec(t_0)$:

Если расписать покоординатно, то получим следующее уравнение:

begin x'(t_0)cdot(X-x(t_0))+y'(t_0)cdot(Y-y(t_0))+z'(t_0)cdot(Z-z(t_0))=0. end

Соприкасающаяся плоскость

Плоскость, проходящую через заданную точку $M$ кривой $gamma$ параллельно векторам $vec(t_0)$, $vec(t_0)$, когда они неколлинеарны, называют соприкасающейся плоскостью кривой.

Если $vec$ — радиус-вектор произвольной точки соприкасающейся плоскости, то ее уравнение можно записать через смешанной произведение трех компланарных векторов $vec-vec(t_0)$, $vec(t_0)$, $vec(t_0)$:

Зная координаты точки и векторов, определяющих плоскость, запишем смешанное произведение через определитель. Получим следующее уравнение соприкасающейся плоскости:

begin left| begin X-x(t_0) & Y-y(t_0) & Z-z(t_0) \ x'(t_0) & y'(t_0) & z'(t_0)\ x»(t_0) & y»(t_0) & z»(t_0) \ end right|=0 end

Бинормаль и главная нормаль

Прямая, проходящая через точку $M$ кривой $gamma$ перпендикулярно касательной к кривой в этой точке, называется нормалью.

Таких кривых можно провести бесконечно много, все они образуют нормальную плоскость. Мы выделим среди нормалей две — бинормаль и главную нормаль.

Нормаль, перпендикулярную соприкасающейся плоскости, называют бинормалью.

Нормаль, лежащую в соприкасающейся плоскости, называют главной нормалью.

Из определения бинормали (перпендикулярна касательной и перпендикулярна соприкасающейся плоскости) следует, что в качестве ее направляющего вектора мы можем взять векторное произведение $ vec(t_0)timesvec(t_0)$, тогда ее уравнение можно записать в виде:

Как и раньше, $vec$ — радиус-вектор произвольной точки бинормали. Каноническое уравнение прямой:

Из определения главной нормали (перпендикулярна касательной и перпендикулярна бинормали) следует, что в качестве ее направляющего вектора можно взять векторное произведение $vec(t_0) timesleft[vec(t_0),vec(t_0)right]$:

Уравнение в каноническом виде распишите самостоятельно.

Спрямляющая плоскость

Плоскость, проходящую через заданную точку $M$ кривой $gamma$ перпендикулярно главной нормали, называют спрямляющей плоскостью.

Другое определение: Плоскость, определяемую касательной к кривой и бинормалью в той же точке, называют спрямляющей плоскостью.

Второе определение позволяет записать уравнение спрямляющей плоскости через смешанное произведение трех компланарных векторов, определяющих эту плоскость $vec-vec(t_0)$, $vec(t_0)$, $vec(t_0)timesvec(t_0)$: begin left(vec-vec(t_0),, vec(t_0),, vec(t_0)timesvec(t_0)right)=0. end Зная координаты соответствующих векторов, можно легко записать это смешанное произведение через определитель, раскрыв который, вы получите общее уравнение спрямляющей плоскости.

Репер Френе

Орт (то есть единичный вектор) касательной обозначим: $$ vec=frac<vec(t_0)><|vec(t_0)|>. $$ Орт бинормали: $$ vec=frac<vec(t_0)timesvec(t_0)><|vec(t_0)timesvec(t_0)|>. $$ Орт главной нормали: $$ vec=frac<vec(t_0) times[vec(t_0),,vec(t_0)]><|vec(t_0) times [vec(t_0),,vec(t_0)]|>. $$

Правая тройка векторов $vec$, $vec$, $vec$ называется репером Френе.

Видео:Записать уравнение прямой параллельной или перпендикулярной данной.Скачать

Решение задач

Задача 1

Кривая $gamma$ задана параметрически:

Точка $M$, принадлежащая кривой, соответствует значению параметра $t=0$. Записать уравнения касательной, бинормали, главной нормали, нормальной плоскости, соприкасающейся плоскости и спрямляющей плоскости, проведенных к данной кривой в точке $M$. Записать векторы репера Френе.

Решение задачи 1

Задачу можно решать разными способами, точнее в разном порядке находить уравнения прямых и плоскостей.

Начнем с производных.

begin 1cdot X+0cdot Y+1cdot (Z-1)=0,, Rightarrow ,, X+Z=1. end

begin left| begin X-0 & Y-0 & Z-1 \ 1 & 0 & 1\ 0 & 2 & 1 \ end right|=0 end Раскрываем определитель, получаем уравнение: begin -2X-Y+2Z-2=0 end

begin 1cdot X-4cdot Y-1cdot (Z-1)=0,, Rightarrow ,, X-4Y-Z+1=0. end

Поскольку направляющий вектор главной нормали у нас был найден как векторное произведение направляющих векторов касательной и бинормали, тройка $vec$, $vec$, $vec$ не будет правой (по определению векторного произведения вектор $vectimesvec$ направлен так, что тройка векторов $vec$, $vec$, $vec=vectimesvec$

— правая). Изменим направление одного из векторов. Например, пусть

Теперь тройка $vec$, $vec$, $vec<tilde>$ образует репер Френе для кривой $gamma$ в точке $M$.

Задача 2

Написать уравнение соприкасающейся плоскости к кривой $$ x=t,,, y=frac,,, z=frac, $$ проходящей через точку $N(0,0,9)$.

Решение задачи 2

Нетрудно заметить, что точка $N$ не принадлежит заданной кривой $gamma$. Следовательно соприкасающаяся плоскость проведена в какой-то точке $M(t=t_0)ingamma$, но при этом плоскость проходит через заданную точку $N(0,0,9)$.

Найдем значение параметра $t_0$.

Для этого запишем уравнение соприкасающейся плоскости, проведенной в произвольной точке $M(t=t_0)$. И учтем, что координаты $N$ должны удовлетворять полученному уравнению.

Соприкасающаяся плоскость определяется векторами $vec(t_0)$, $vec(t_0)$, поэтому записываем определитель begin left| begin X-t_0 & Y-t_0^2/2 & Z-t_0^3/3 \ &&\ 1 & t_0 & t^2_0 \ &&\ 0 & 1 & 2t_0 end right|=0 quad Rightarrow end

begin (X-t_0)cdot t_0^2 — (Y-t_0^2/2)cdot 2t_0 + (Z-t_0^3/3)=0. end Подставляем вместо $X$, $Y$, $Z$ координаты точки $N$: $X=0$, $Y=0$, $Z=9$, упрощаем и получаем уравнение относительно $t_0$: begin 9-t_0^3/3=0 quad Rightarrow quad t_0=3. end Подставив найденное $t_0$ в записанное ранее уравнение, запишем искомое уравнение соприкасающейся плоскости: $$ 9X-6Y+Z-9=0. $$

Задача 3

Через точку $Pleft(-frac45,1,2right)$ провести плоскость, являющуюся спрямляющей для кривой: $$ x=t^2,,, y=1+t,,, z=2t. $$

Решение задачи 3

Как и в предыдущей задаче нам неизвестны координаты точки, в которой проведена спрямляющая плоскость к заданной кривой. Найдем их.

Спрямляющая плоскость определяется касательной и бинормалью, то есть векторами $vec(t_0)$ и $vec(t_0)timesvec(t_0)$.

Записываем уравнение спрямляющей плоскости: begin left| begin X-t_0^2 & Y-1-t_0 & Z-2t_0 \ 2t_0 & 1 & 2\ 0 & 4 & -2 end right|= 0 end

Раскрываем определитель. Подставляем в уравнение координаты точки $P$: $X=-4/5$, $Y=1$, $Z=2$. Упрощаем и получаем уравнение для нахождения $t_0$: begin 5t_0^2-8t_0-4=0 ,, Rightarrow ,, t_=2,, t_=-frac25. end

Уравнения соприкасающихся плоскостей к заданной кривой, проходящих через $P$, принимают вид: begin & 5X-4Y-8Z+24=0,\ & 25X+4Y+8Z=0. end

📽️ Видео

10 класс, 43 урок, Уравнение касательной к графику функцииСкачать

Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.Скачать

§31.1 Приведение уравнения кривой к каноническому видуСкачать

53. Приведение общего уравнения кривой к каноническому видуСкачать

Кривые второго порядкаСкачать

Уравнение окружности (1)Скачать

Аналитическая геометрия, 7 урок, Линии второго порядкаСкачать

Как написать уравнения касательной и нормали | МатематикаСкачать

Лекция 31.1. Кривые второго порядка. ЭллипсСкачать