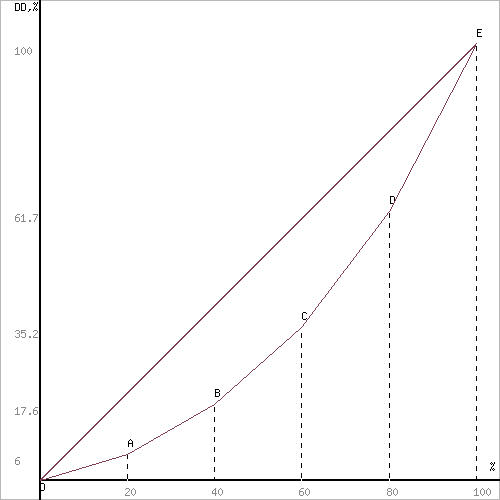Кривая лоренца распределения дохода в некоторой стране задана уравнением (3 видео)

Кривая Лоренца

Дифференциация заработной платы предопределяет неравенство в распределении доходов.
Дифференциация доходов населения — это объективно складывающиеся различия в уровне доходов индивидов и социальных групп, обусловленные различиями в оплате труда и социальных выплат, способностях и предприимчивости, имущественном положении.
Денежные доходы населения включают в себя заработную плату, социальные трансферты, предпринимательские доходы, проценты, дивиденды и другие доходы от собственности, а также общую стоимость продукции –личного подсобного хозяйства, потребленной в семье и проданной. Доходы населения распределяются по группам населения неравномерно.
Помимо анализа распределения доходов населения, кривую Лоренца также используют при конкурентном анализе.

Пример №1 . На основе данных таблицы:

Рассчитайте коэффициент Джини
Постройте кривую Лоренца.

Социальная группа населения	Численность населения, %	Денежные доходы, %
1.	20	6,0
2.	20	11,6
3.	20	17,6
4.	20	26,5
5.	20	38,3
Итого	100	100,0

Денежные доходы населения

Группы по денежным доходам, %	Доля денежных доходов в группе, %
20	6
40	11.6
60	17.6
80	26.5
100	38.3

Линия фактического неравенства строится на основании данных о процентах дохода приходящихся на каждые 20 % населения.
Если нижняя первая часть населения получила 6.0% всех доходов, то графически это будет точка А. Чтобы получить точку В необходимо сложить процент дохода первых 20 % населения с процентами доходов вторых 20 % населения (6.0% + 11.6%) и т.д.

20-ти процентные группы населения	Объем денежных доходов населения, в % к итогу	Доля денежных доходов нарастающим итогом, %	Площадь треугольника	Площадь прямоугольника	Общая площадь фигуры, S_i
20	6	6	60	0	60
40	11.6	17.6	116	120	236
60	17.6	35.2	176	352	528
80	26.5	61.7	265	704	969
100	38.3	100	383	1234	1617
3410

Чтобы построить кривую Лоренца откладываем по оси Х значения 1-го столбца, а по оси Y значения 3-го столбца.

2. Индекс Джини.
Для исчисления коэффициента Джини необходимо рассчитать величины p_i и q_i. Здесь q_i — доля денежных доходов нарастающим итогом (столбец №3 табл.1) деленная на 100.

p_i	q_i	p_iq_i+1	p_i+1q_i
0.2	0.06	0.0352	—
0.4	0.18	0.14	0.024
0.6	0.35	0.37	0.11
0.8	0.62	0.8	0.28
1	1	—	0.62
ВСЕГО	1.3462	1.0282

Коэффициент Джини равен: K_L = ∑p_iq_i+1 — ∑p_i+1q_i = 1.3462 — 1.0282 = 0.318

Пример №2 . Имеются следующие данные о распределении доходов населения региона по трем группам и доле населения в каждой группе:

	1 группа	2 группа	3 группа
Доходы населения по группам (руб.)	5000-10000	10000-20000	20000-30000
Доля населения в группе	0,15	0,60	0,25

Определить коэффициент концентрации доходов Джинни.
Решение.
Необходимо найти доли среднего дохода на человека в каждой группе, в виде отношения среднего дохода группы к суммарному среднему доходу, и соответствующие накапливаемые частоты этих долей. Чем ближе значение коэффициента к единице, тем выше уровень дифференциации доходов.

	1 группа	2 группа	3 группа	Итого
Доходы населения по группам (руб.)	5000-10000	10000-20000	20000-30000
Среднее значение дохода в группе, руб.	7500	15000	25000	47500
Доля доходов в группе, %	15,8	31,6	52,6	100,0

Далее решается через калькулятор.

Доля доходов в группе, %	Доля населения в группе
15,8	0,15
31,6	0,6
52,6	0,25

Пример №3 . Дать графическое изображение вариационного ряда, приведенного в таблице (гистограмма, полигон, кумулята). Определить средние величины (меры положения) – среднюю арифметическую, моду, медиану, вычислить квартили и показатели вариации – среднее абсолютное отклонение, дисперсию, среднее квадратическое отклонение, относительный квартильный размах, коэффициент вариации. Построить кривую (ломаную) Лоренца, вычислить коэффициент концентрации дохода (индекс Джини). Пояснить статистический, физический, экономический или иной смысл вычисленных величин.

№ группа	Среднедушевые доходы населения (тыс. руб.)	Количество насосов
1	0-30	10
2	30,1-60	14
3	60,1-90	19
4	90,1-120	25

Пример №4 . Исходные данные:

%	Доход
10	2.3
20	4.5
30	4.7
40	6
50	7.5
60	10.2
70	14.1
80	16.7
90	18.5
100	15.5

Линия фактического неравенства строится на основании данных о процентах дохода приходящихся на каждые 10% населения. Если нижняя первая часть населения получила 2.3% всех доходов то графически это будет точка А. Чтобы получить точку В необходимо сложить процент дохода первых 10% населения с процентами доходов вторых 10% населения (2.3% + 4.5%) и т.д.

%	Доход	S=S_i+S_i-1	Площадь треугольника	Площадь	Сумма
10	2.3	2.3	11.5	0	11.5
20	4.5	6.8	22.5	23	45.5
30	4.7	11.5	23.5	68	91.5
40	6	17.5	30	115	145
50	7.5	25	37.5	175	212.5
60	10.2	35.2	51	250	301
70	14.1	49.3	70.5	352	422.5
80	16.7	66	83.5	493	576.5
90	18.5	84.5	92.5	660	752.5
100	15.5	100	77.5	845	922.5
Итого	3481

Чтобы построить кривую Лоренца откладываем по оси Х откладываем значения столбца Процент (%), а по сои Y значения столбца S.

Рассчитаем коэффициенты концентрации доходов (индекс Джини)

Уровень неравенства определяется с помощью коэффициента Джини.

Он рассчитывается как отношение площади фигуры OABCDKLMNPE к площади треугольника ОEG.

Для того чтобы определить площадь фигуры, лежащей ниже кривой Лоренца, соединяем прямыми линиями точки ОА, АВ и т.д.

Опускаем перпендикуляр на ось X и находим площади фигур, лежащих ниже точек А, B , С.

Площадь S_ABB’A состоит из треугольника и прямоугольника S_BCCB’ также состоит из треугольника и прямоугольника.

Сложив все площади фигур, получим площадь фигуры S₂.

Площадь треугольника OEG находим по формуле:

1/2 *100%*100% = 5000

Отсюда индекс Джини равен:

I = 1519 / 5000 = 0.3038

Децильный коэффициент дифференциации доходов

Содержание

Кривые Лоренца распределения дохода в некоторых странах могут быть заданы уравнениями
Условие
Решение
Зарегистрируйся, чтобы продолжить изучение работы
Задачи по экономической теории. Часть 04 (кривая Лоренца)
Задача №294 (задача по кривой Лоренца)
💡 Видео

Видео:Кривая Лоренца и индекс Джини - измеряем неравенство доходовСкачать

Кривые Лоренца распределения дохода в некоторых странах могут быть заданы уравнениями

Реферат.Справочник
Контрольные работы по статистике
Кривые Лоренца распределения дохода в некоторых странах могут быть заданы уравнениями

Условие

Кривые Лоренца распределения дохода в некоторых странах могут быть заданы уравнениями: а) 𝑦 = 0,85 ∙ 𝑥2 + 0,15 ∙ 𝑥; б) 𝑦 = 2𝑥 − 1; в) 𝑦 = 0,7 ∙ 𝑥3 + 0,3 ∙ 𝑥2. Какую часть дохода получат 10 % наиболее низкооплачиваемого населения? Вычислить коэффициенты Джини для этих стран.

Решение

А) Рассчитаем часть дохода, которую при данной кривой Лоренца получают 10% наиболее низкооплачиваемого населения:
или 2,35%.
Рассчитать коэффициент Джини можно как отношение площади фигуры, образованной кривой Лоренца и кривой равенства, к площади треугольника, образованного кривыми равенства и неравенства . В случае полного равенства коэффициент будет равен 0; в случае полного неравенства он будет равен 1. Иначе говоря, следует найти площадь первой фигуры и поделить её на площадь второй:
J = Sф/Sтр
Площадь треугольника, образованного кривыми равенства и неравенства равна Sтр = 1*1/2 = 0,5.
Площадь фигуры:
Sф = Sтр – S1,
S1 – площадь фигуры под кривой Лоренца.
Для наших данных:
;
Sф = 0,5 – 0,3583 = 0,1417;
J = 0,1417/0,5 = 0,2834.
б) Рассчитаем часть дохода, которую при данной кривой Лоренца получают 10% наиболее низкооплачиваемого населения:
или 7,177%.
Коэффициент Джини:
.
Sф = 0,5 – 0,4427 = 0,0573;
J = 0,0573/0,5 = 0,1146.
в) Рассчитаем часть дохода, которую при данной кривой Лоренца получают 10% наиболее низкооплачиваемого населения:
или 0,37%.
Коэффициент Джини:
.
Sф = 0,5 – 0,275 = 0,225;
J = 0,225/0,5 = 0,45.

Зарегистрируйся, чтобы продолжить изучение работы

. В случае полного равенства коэффициент будет равен 0; в случае полного неравенства он будет равен 1. Иначе говоря, следует найти площадь первой фигуры и поделить её на площадь второй:
J = Sф/Sтр
Площадь треугольника, образованного кривыми равенства и неравенства равна Sтр = 1*1/2 = 0,5.
Площадь фигуры:
Sф = Sтр – S1,
S1 – площадь фигуры под кривой Лоренца.
Для наших данных:
;
Sф = 0,5 – 0,3583 = 0,1417;
J = 0,1417/0,5 = 0,2834.
б) Рассчитаем часть дохода, которую при данной кривой Лоренца получают 10% наиболее низкооплачиваемого населения:
или 7,177%.
Коэффициент Джини:
.
Sф = 0,5 – 0,4427 = 0,0573;
J = 0,0573/0,5 = 0,1146.
в) Рассчитаем часть дохода, которую при данной кривой Лоренца получают 10% наиболее низкооплачиваемого населения:
или 0,37%.
Коэффициент Джини:
.
Sф = 0,5 – 0,275 = 0,225;
J = 0,225/0,5 = 0,45.

Оплатите контрольную работу или закажите уникальную работу на похожую тему

Видео:9.3 Неравенство доходовСкачать

Задачи по экономической теории. Часть 04 (кривая Лоренца)

Задача №294 (задача по кривой Лоренца)

Население страны состоит из 5 чел., получающих доходы в размере 500 долл., 350 долл., 250 долл., 75 долл., 50 долл. Построить кривую Лоренца для такой экономики из 5 человек и дать необходимые пояснения.

Кривая Лоренца – кривая, которая демонстрирует фактическое деление доходов в обществе и дает наглядное представление о его отклонении от линии абсолютного равенства в делении доходов и о степени неравенства их деления. Кривая Лоренца применяется в макроэкономическом анализе реального деления доходов, отображает влияние фискальной политики государства на перераспределение доходов и уменьшения имущественного неравенства в обществе. Для построения кривой Лоренца нужны статистические данные о том, сколько семей (в %) получили определенную долю совокупного дохода населения страны.

Коли-
чество насе-
ления, чел.

В % общего коли-
чества насе-
ления

Кумуля-
тивный объем насе-
ления, в %

Объем доходов, долл.

Кумуля-
тивный объем доходов, в %

По приведенным данным построена кривая Лоренца:

Проанализируем полученные результаты.
Если совокупный доход и количество населения принять соответственно за 100%, точка А покажет, что 100% дохода распределено среди 100% населения, точка Е – 50% дохода приходится на 50% население и т.д. Линия ОЕА – абсолютное равенство в делении доходов, на которой в любой точке доход распределяется среди населения абсолютно равномерно. Графически прямая ОЕА делит квадрат на два ровных треугольника, боковые стороны которого характеризуют крайнюю степень имущественного неравенства (например, в точке С 100% доходу приходится на 1 получателя).
Линии ОС и АС – это линии абсолютного неравенства; ОЕА – это линии абсолютного равенства.
В любом обществе деление доходов не равномерно. Если бы кривая Лоренца совпадала с линией абсолютного равенства, то это свидетельствовало бы об абсолютно уравнительном характере деления доходов, при совпадении кривой Лоренца с осями координат (ОС и АС) — о крайней степени неравенства. Площадь между кривой Лоренца и линией абсолютного равенства характеризует степень неравенства в делении доходов, ее определяют с помощью коэффициента Джини, который характеризует удельный вес площади (ОЕАД), образованной кривой Лоренца и линией абсолютного равенства, у площади треугольника абсолютного неравенства (ОЕАС). Вопрос о степени приемлемого для общества имущественного неравенства – одно из самых болезненных в экономической теории и социально-экономической политике. Попытки приблизить кривую Лоренца к прямой абсолютного равенства доходов уменьшением дифференциации доходов, ликвидацией частной собственности, как засвидетельствовал исторический опыт, приводят к мотивационному кризису. В то же время избыточная дифференциация влечет опасное социальное напряжение, социально-политические потрясения. Учитывая это, экономисты ученых считают, что граница натяжения кривой Лоренца наступает в случае, когда самое бедное 40% население начинает получать все вместе менее как 12-13% от общей суммы доходов семей страны. В данном случае эта величина составляет 10,2%. Кроме того, усиление имущественного расслоения граждан во время экономического взлета не такое опасно для социальной стабильности, как во время экономического кризиса, что может иметь серьезные социально-политические следствия.
Механизм решения этого противоречия предусматривает два основных элемента: 1) прогрессивное налогообложение личных доходов; 2) систему государственной социальной поддержки самых бедных граждан. Осуществляя активную фискальную политику, государство способствует уменьшению имущественного неравенства.