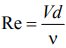Критерий рейнольдса для ламинарного режима связан с критерием архимеда уравнением

Видео:Вязкость. Ламинарное и турбулентное течения жидкостей. 10 класс.Скачать

Основы гидравлики

Видео:Режимы течения жидкости, ламинарный и турбулентный режимыСкачать

Режимы движения реальных жидкостей

Наверняка каждому приходилось наблюдать за водным потоком в различных естественных и искусственных руслах — реках, каналах, протоках и т. п. И любой наблюдатель, даже самый невнимательный, заметит, что в равнинных реках вода размеренно протекает словно единый жидкий массив со спокойной и ровной поверхностью, в горных реках с бешеным ревом несется бурлящим потоком, разбрасывая брызги с кипящей поверхности, взволнованной всплесками перемешивающихся струй.
Подвижная вода, словно живое существо, по-разному ведет себя с изменением условий, характеризующих ее путь. Таким же поведением характеризуется не только водный поток, но и поток любой другой жидкости.

Почему так происходит, и в какой момент в спокойном и ласковом потоке вдруг просыпается безумный бурлящий «демон»? Можно ли предсказать поведение потока в тех или иных условиях?
Давайте попробуем разобраться в этом вопросе с точки зрения современной науки.

Рассмотрим потоки, характеризуемые условием неразрывности – в любой момент времени расход жидкости постоянен во всех сечениях, т. е соблюдается соотношение:

v ₁S₁ = v ₂S₂ = v ₃S₃ = … = v S ,

где v ₁ , v ₂ , v ₃ ,…v – соответственно средние скорости потока в разных сечениях.

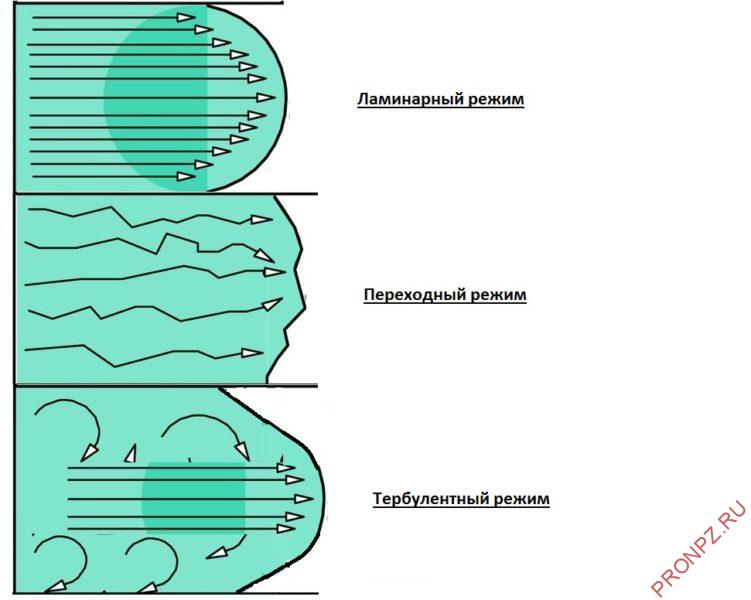
Наблюдения за такими потоками показывают, что в природе существуют два различных вида движения жидкости: во-первых, слоистое, упорядочное или ламинарное движение , при котором отдельные слои жидкости скользят друг относительно друга, не смешиваясь между собой, и, во-вторых, неупорядоченное, так называемое турбулентное движение , когда частицы жидкости движутся по сложным, все время изменяющимся траекториям и в жидкости происходит интенсивное перемешивание частиц и слоев.

Иногда выделяют третий режим движения жидкостей — переходный, при котором упорядоченное движение частиц очень неустойчиво, и при малейшем изменении условий перемещения потока может произойти переход от ламинарного режима к турбулентному, и наоборот.

Число Рейнольдса

Наблюдательными людьми давно подмечено, что вязкие жидкости (например, масла) движутся большей части упорядоченно, а маловязкие жидкости (вода, бензин, газообразные вещества) — почти всегда неупорядоченно.
Кроме того, на характер движения жидкости явно влияет скорость потока — медленно перемещающаяся по руслу жидкость ведет себя спокойно, но стоит увеличить ее скорость, и картина может измениться. Однако установить математическую зависимость между характером движения потока и его параметрами долгое время не удавалось никому.
Ясность в вопрос о том, как именно будет происходить движение жидкости в тех или иных условиях, была внесена в 1883 году в результате опытов английского физика О. Рейнольдса.

О. Рейнольдс определил общие условия, при которых возможны существование ламинарного и турбулентного режима движения жидкости и переход от одного режима к другому. Оказалось, что состояние (режим) потока жидкости в трубе зависит от величины некоторого безразмерного числа, учитывающего основные факторы, определяющие это движение: среднюю скорость, диаметр трубы (или другие линейные характеристики потока) , плотность жидкости и ее вязкость.

Влияние всех этих величин на характер движения жидкости объединены в формуле, выражающей число Рейнольдса:

Re = ρ v R/µ ,

где: R – гидравлический радиус потока; v – скорость потока; µ — динамическая вязкость жидкости, ρ – плотность жидкости.

Число Рейнольдса (иногда его называют критерием Рейнольдса) является безразмерной величиной.

Осборн Рейнольдс (Osborne Reynolds, 1842-1912) — английский механик, физик и инженер, специалист в области гидромеханики и гидравлики. Член Лондонского королевского общества с 1877 г.
В 1883 г. он установил общий принцип прогнозирования режима движения жидкости при помощи упомянутого выше числа. Выводами и умозаключениями Рейнольдса потомки пользуются и в наши дни при гидравлических расчетах. Тем не менее, несмотря на то, что вопрос о неустойчивости ламинарного движения и его переходе в турбулентное, а также о величине критического числа Рейнольдса долгое время является предметом тщательных теоретических и опытно-экспериментальных исследований, до сих пор его полного решения так и не получено.

Поскольку динамическая вязкость жидкости связана с кинематической вязкостью соотношением µ = ρν , то критерий Рейнольдса можно записать в виде:

Re = v R/ν (1) .

Число Рейнольдса определяет границы, между которыми режим движения жидкости может принимать ламинарный или турбулентный характер.
Эти границы характеризуются критическими значениями числа Рейнольдса: нижним Re_кр и верхним Re’_кр .
При Re наблюдается устойчивый ламинарный режим течения жидкости, при Re > Re’_кр – устойчивый турбулентный режим, а в интервале чисел Рейнольдса Re’_кр> Re > Re_кр режим течения жидкостей неустойчивый, т. е. ламинарный режим может легко переходить в турбулентный.

Формулу (1) применяют при определении числа Рейнольдса для потока любого сечения.
Для круглых цилиндрических труб с внутренним диаметром d :

Red = v d/ν .

Поскольку для таких труб гидравлический радиус R = 4d , то

Re = 4Red = 4 v d/ν .

При проведении гидравлических расчетов цилиндрических труб обычно принимают Re = 250…500, Re’_кр = 575. При этом Re_d будет равен: Red_кр = 1000…2000, Red’_кр = 2300.

Проведенные исследования показывают также, что критическое значение числа Рейнольдса увеличивается в сужающихся трубах и уменьшается в расширяющихся. Это можно объяснить тем, что при ускорении движения частиц жидкости в сужающихся трубах их тенденция к поперечному перемешиванию уменьшается, а при замедленном течении в расширяющихся трубах увеличивается.

По критическому значению числа Рейнольдса легко можно определить также критическую скорость, т. е. скорость, ниже которой будет иметь место ламинарное движение жидкости:

v _кр = Re_крv/d = 2300v/d .

Ламинарному и турбулентному режимам движения жидкости соответствует и различное распределение скоростей частиц по живому сечению потока.

При ламинарном режиме течения жидкости по трубе (см. рис. 1) максимальная скорость наблюдается у частиц жидкости, движущихся по центральной оси трубы, а минимальная – у стенок трубы. Частицы подвижной жидкости, расположенные у стенок трубы буквально «прилипают» к стенкам благодаря силам трения и практически неподвижны.
По мере удаления от стенок трубы скорость частиц жидкости возрастает, поскольку на их движение влияет лишь трение между отдельными слоями (элементарными струйками) жидкости. Исследования показали, что при ламинарном режиме движения жидкости изменение скорости в поперечном сечении потока происходит по параболическому закону, т. е. эпюру скоростей частиц можно представить в виде параболы (см. рис. 1) .

При турбулентном режиме течения жидкости распределение скоростей более равномерное по сечению потока, чем при ламинарном режиме. Это связано с перемешиванием частиц жидкости, имеющих разную скорость в слоях, и относительным выравниванием средней скорости на всей площади сечения потока. Т. е. отдельные частицы турбулентного потока могут иметь в одном и том же сечении весьма различные по величине и направлению скорости, однако эпюра (график) средней скорости всех частиц по сечению будет ровнее, чем при ламинарном режиме движения.
Лишь слои жидкости, прилегающие к стенкам трубы (поз. 1 на рисунке) , движутся с малой скоростью, и режим движения здесь наблюдается ламинарный, несмотря на то, что весь поток характеризуется турбулентным режимом движения.

По этой причине можно утверждать, что «чистого турбулентного режима» движения жидкости не существует, поскольку граничные со стенками слои жидкости в любом случае имеют ламинарный характер движения. Однако толщина ламинарного слоя несравненно мала в сравнении с сечением потока, в котором частицы жидкости перемещаются хаотично (турбулентно) , поэтому такой режим течения жидкости принято считать турбулентным.

Пример решения задачи с использованием числа Рейнольдса

Определить режим движения нефти в трубопроводе диаметром d = 400 мм при скорости движения v = 0,13 м/с.
Кинематическая вязкость нефти ν = 0,3×10 -4 м 2 /с.

Определим число Рейнольдса для данного режима движения жидкости (нефти) :

Re_d = v d/ν = 0,13×0,4/0,3×10 -4 = 1733.

Для круглых труб критические значения числа Рейнольдса имеют величину: Re_dкр = 1000…2000, Re’_dкр = 2300.
Сравнив полученное расчетное значение с критическими значениями числа Рейнольдса, делаем вывод, что Re_d , т. е. движение нефти в трубопроводе будет ламинарным.

Другие задачи на использование числа Рейнольдса для определения режимов движения жидкостей представлены здесь.

Видео:Урок 138. Число Рейнольдса. Критерий Рейнольдса.Скачать

Число Рейнольдса

Движение жидкости, несмотря на кажущуюся на первый взгляд, беспорядочность движения имеет определенные закономерности. Рейнольдс в своих опытах нашел определенные общие условия, при которых возможно существование того или иного режима течения и переход от одного режима к другому.

При проведении опытов Рейнольдс в 1883г. подтвердил существование двух режимов течения жидкости. Ему удалось вычислить безразмерное число, описывающее характер потока вязкой жидкости

Содержание статьи

Видео:Урок 132. Основные понятия гидродинамики. Уравнение непрерывностиСкачать

Опыты Рейнольдса

Эксперименты О.Рейнольдса показали, что при движении жидкости , последняя теряет определенное количество энергии. Эти потери зависят от особенностей движения частиц жидкости в потоке и от самого режима течения.

Опыты проводились на специальном лабораторном стенде, который представлял собой заполненный водой бак Б к которому в нижней части присоединена стеклянная трубка Т. На конце трубки установлен кран К для регулирования расхода жидкости. Расход измеряется с помощью секундомера и мерного бочка М. Бак Б постоянно заполняется водой. Над баком Б расположена ёмкость с краской С. По тонкой трубочке Т1 краска попадает в жидкость, движущуюся в трубке Т. Подачу краски регулирует кран Р.

Опыт №1. Немного приоткрываем кран К. При этом в трубке Т начинается движение жидкости. Открываем кран Р и добавляем в жидкость краску. При небольшой скорости движения в трубке Т краска становится прямолинейной и резко выделяющейся в потоке воды цветной струйкой. Эта струйка не перемешивается с остальной жидкостью. Если ввести в жидкость краску несколькими струйками, то они так и будут двигаться не перемешиваясь с остальной водой.

Движение жидкости, наблюдаемое при малых скоростях, при котором отдельные струйки жидкости движутся параллельно друг другу и оси потока, называют ламинарным (от латинского ламина — слой) или струйчатым движением (режимом). Ламинарное движение может рассматриваться как движение отдельных слоев жидкости, происходящее без перемешивания частиц. Подробнее о ламинарном режиме здесь.

Опыт №2 При намного большем открытии крана струйка краски начинает искривляться и становится волнообразной. Открывая кран ещё больше и увеличивая скорость потока мы увидим, что струйка краски распадается на отдельные вихри и перемешивается с остальной массой воды

Движение жидкости, которое наблюдается при больших скоростях, называется турбулентным (по латински турбулентус — вихревой) движением (режимом). В этом случае в движении жидкости нет видимой закономерности. Отдельные частицы перемешиваются между собой и движутся по самым причудливым, все время меняющимся траекториям весьма сложной формы. Поэтому такое движение называется беспорядочным. Подробнее о турбулентном режиме здесь.

Вывод формулы

Рейнольдс установил, что основными факторами, определяющими характер режима являются:
средняя скорость движения жидкости υ,
диаметр трубопровода d,
плотность жидкости ρ,
абсолютная вязкость жидкости μ

При этом чем больше размеры поперечного сечения и плотность жидкости и чем меньше её вязкость, тем легче при увеличении скорости осуществить турбулентный режим.

Для характеристики режима движения жидкости Рейнольдсом был выведен безразмерный параметр Re, учитывающий влияние перечисленных выше факторов, называемый число Рейнольдса. Таким образом формула

Поскольку μ / ρ = ν , где ν – кинематическая вязкость жидкости, то формула меняет вид на

Число Рейнольдса и режимы течения.

Границы существования того или иного режима движения жидкости определяются двумя критическими значениями числа Рейнольдса:
нижнее критическое числом Рейнольдса Re_{кр. н.}
верхнее критическое числом Рейнольдса Re_{кр. в.}

Значение скорости, соответствующее этим значениям Re называют критическими.

При значениях числа Рейнольдса Re Re_{кр. в.} – только турбулентный. При Re_{кр. н.} 2300 – всегда турбулентный режимы.

При этом движении жидкости в неустойчивой зоне исключается из особого рассмотрения, это приводит к некоторому запасу и большей надежности в гидравлических расчетах в случае, если в этой зоне действительно имеет место ламинарный режим.

Без особого труда можно получить значения для Reкр для любой формы сечения, а не только круглой формы. Вспоминая, что при круглом сечении радиус

подставляем в формулу для определения числа Рейнольдса

Принимая для критического числа Рейнольдса независимо от формы живого сечения величину Re_кр. = 2300, находим, что для сечения любой формы критериев для сужения о характере режима движения является величина, равная 2300 / 4 = 575.

Таким образом, режим ламинарный если значение числа Рейнольдса

И режим турбулентный, если

Видео по теме.

На практике в большинстве случаев (движение воды в трубах, каналах, реках) приходится иметь дело с турбулентным режимом. Ламинарный режим встречается реже. Он наблюдается, например, при движении в трубах очень вязких жидкостей, что иногда имеет место в нефтепроводах, при движении жидкости в очень узких трубках и порах естественных грунтов.

Видео:Число РейнольдсаСкачать

Формула числа Рейнольдса Re

Видео:Число Рейнольдса Критерии РейнольдсаСкачать

Калькулятор для расчета Re онлайн

Расчет по общей формуле

Расчет Re для воды

Расчет Re для воздуха

Видео:1. Определение числа РейнольдсаСкачать

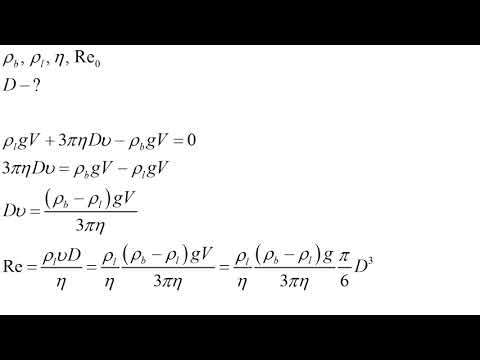
Формула

Расчетная формула числа Рейнольдса Re в общем виде:

где — плотность среды, кг/м 3 ; — характерная скорость, м/с; — гидравлический диаметр, м; — динамическая вязкость среды, Па·с или кг/(м·с); — кинематическая вязкость среды ( ), м 2 /с; — объёмный расход потока, м 3 /с; — площадь сечения канала, например, трубы, м 2 .

Для труб круглого сечения расчетная формула числа Рейнольдса Re будет:

• V — характерная скорость, м/с;
• d — внутренний диаметр трубы, м;
• — кинематическая вязкость среды ( ), м 2 /с;

Видео:Определение режима движения жидкости. Число Рейнольдса.Скачать

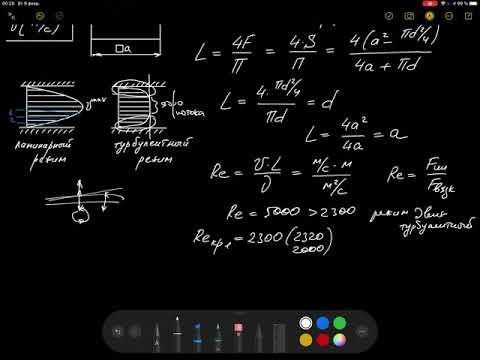
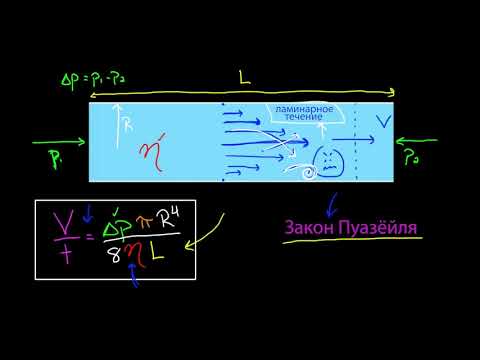
Физический смысл

Физический смысл – число Рейнольдса Re характеризует смену режимов течения от ламинарного к турбулентному. Re является критерием подобия течения вязкой жидкости.

Критерий назван в честь выдающегося английского физика Осборна Рейнольдса (1842—1912).

В настоящее время не существует строгого научно доказанного объяснения этому явлению, однако наиболее достоверной гипотезой считается следующая: смена режимов движения жидкости определяется отношением сил инерции к силам вязкости в потоке жидкости. Если преобладают первые, то режим движения турбулентный, если вторые – ламинарный.

Видео:Урок 66 (осн). Усложненные задачи на закон АрхимедаСкачать

Режимы течения

Режим течения в динамическом пограничном слое зависит от числа Рейнольдса Re и может быть:

1. Ламинарный режим – слоистое течение без перемешивания частиц жидкости и без пульсации скорости и давления, все линии тока направлены параллельно.
2. Турбулентный режим – течение, сопровождающееся интенсивным перемешиванием жидкости с пульсациями скоростей и давлений, наряду с основным продольным перемещением жидкости наблюдаются поперечные перемещения и вращательные движения отдельных объемов жидкости.

Эпюры скоростей

Видео:Турбулентность на высоких скоростях и число Рейнольдса ( видео 15) | Жидкости | ФизикаСкачать

Критическое значение

Переход к турбулентному режиму течения жидкости в пограничном слое определяется критическим значением числа Рейнольдса. Это обусловлено тем, что при возрастании скорости, участвующей в расчете числа Re, его значение растет.
Таким образом, переход от ламинарного режима к турбулентному наблюдается при определенной скорости движения жидкости. Эта скорость называется критической Vкр.

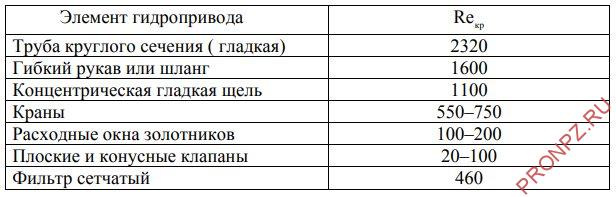
Значение критического числа Re для различных элементов гидропривода

Видео:Алексей Венедиктов* и Сергей Бунтман / Будем наблюдать / 20.01.24Скачать

Размерность

Числе Re не имеет единиц измерения. Re является безразмерным критерием подобия течения вязкой жидкости.

Видео:Уравнение Рейнольдса-МКМРО3-14-лек-Ахметова А.У.Скачать

Течение в трубе

При ламинарном течении жидкости в прямой трубе или канале постоянного сечения все линии тока направлены параллельно оси трубы, при этом отсутствуют поперечные перемещения частиц жидкости.

При турбулентном течении в канале наряду с основным продольным перемещением жидкости в трубе наблюдаются поперечные перемещения и вращательные движения отдельных объемов жидкости.

Зависимость режима течения от значения числа Re в гладких трубах:

• 2300 – Турбулентный режим

Обычно предполагается, что при числе Re выше 2300 образуется турбулентный режим.

Тем не менее, при значениях Re выше критического и до определённого предела наблюдается переходной (смешанный) режим течения жидкости, когда турбулентное течение более вероятно, но ламинарное в некоторых конкретных случаях тоже наблюдается — так называемая неустойчивая турбулентность. В трубах такой переходный интервал может достигать вплоть до Re = 2300—10 000.

Видео:Подобие процессов конвективного теплообменаСкачать

Процессы и аппараты химической технологии. Гидромеханические процессы (стр. 3 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4

В таблице 1.2 приведена классификация процессов разделения неоднородных систем по движущей силе.

Основная движущая сила

Осаждение или фильтрование

Фильтрующая центрифуга. Осадительная центрифуга

Сила электрического поля

Таблица 1.2

Осаждением называется процесс разделения жидких и газовых неоднородных систем (суспензий, пылей) путём выделения твёрдых частиц. Осаждение под действием силы тяжести называется отстаиванием. В основном отстаивание применяется для предварительного грубого разделения неоднородных систем. Осаждение связано с движение твёрдых частиц в жидкости или газе.

Рассмотрим движение шарообразной частицы в неподвижной среде (рис. 2.1). При движении тела в жидкости или при обтекании его движущейся жидкостью возникают сопротивления для преодоления которых, а так же обеспечения равномерного движения тела должна быть затрачена определенная энергия. Величина возникающего сопротивления зависит от режима движения и формы обтекаемого тела.

Рис.2.1 Действие сил на твердую частицу, движущуюся в неподвижной среде

Если шарообразная частица весом G будет падать под действием собственного веса, то скорость ее первоначально возрастет, однако с ростом скорости начнет увеличиваться и сопротивление движению частицы со стороны среды. Одновременно произойдет уменьшение ее ускорения и через короткий промежуток времени наступит динамическое равновесие – сила тяжести станет равна силе сопротивления среды, и частица начнет двигаться с постоянной скоростью – скоростью осаждения. Баланс сил в этом случае будет:

,

где — сила тяжести, равная весу частицы; — выталкивающая сила Архимеда, равная весу жидкости в объёме тела; — сила сопротивления среды.

; ;

, где — диаметр частицы; — плотность среды; плотность твердой частицы; скорость осаждения; — коэффициент сопротивления среды (безразмерный).

В развернутом виде уравнение (2.1) примет вид:

,

откуда скорость осаждения будет равна:

,

Расчёт скорости осаждения по уравнению (2.2) затруднён, т. к. коэффициент сопротивления зависит от критерия Рейнольдса, в который входит неизвестная .

Критерий Рейнольдса для процесса осаждения рассчитывается по формуле:

.

Существуют три режима осаждения: ламинарный, переходный и турбулентный.

При ламинарном режиме осаждения (рис. 2.2 а) жидкость обтекает частицу плавно без образования вихрей. Скорость и размер частиц при этом небольшой, но велика вязкость среды. Энергия тратится только на преодоление сил трения. С увеличением скорости осаждения (при переходном режиме) в потоке все большую роль начинают играть силы инерции, которые приводят к отрыву пограничного слоя от поверхности тела, что способствует понижению давления за движущимся телом в непосредственной близости от него и образованию завихрений (рис.2.2 б). При турбулентном режиме осаждения за частицей движется вихревой поток (рис.2.2 в).

Рис.2.2. Движение шарообразной частицы в жидкости.

При ламинарном режиме (область действия закона Стокса) Re 500 и ).

При ламинарном режиме скорость осаждения определяют по формуле Стокса:

Значение зависит от Re, для оценки которого необходимо знать скорость осаждения.

Расчёт скорости осаждения начинают с определения критерия Архимеда (1.39), при известном диаметре частиц d. В не входит скорость осаждения

.

Рассчитав , определяют режим осаждения. Зная зависимость между Рейнольдсом и Архимедом для данного режима (стр. 36), находят критерий Рейнольдса и далее скорость осаждения: .

При ламинарном режиме Ar36, переходном 36Ar83000 и турбулентном — Ar>83000.

Зависимость между критериями и следующая:

Для ламинарного режима , переходного и турбулентного , где — коэффициент формы (или фактор), учитывающий отличие формы частицы от шара. Для частиц неправильной формы скорость осаждения меньше, поэтому скорость, рассчитанную для шарообразной частицы, умножают на поправочный коэффициент ψ, который );

3. При подаче поршневым или центробежным насосом

(до );

4. Под гидравлическим давлением слоя суспензии

(до ).

При фильтровании вязких жидкостей с небольшим содержанием мелких твёрдых частиц, последние проникают в поры перегородки и задерживаются в них. При этом почти не образуется слой осадка. Такой процесс называется фильтрованием с закупориванием пор. Такого фильтрования стараются избегать. т. к. трудно извлечь из пор твёрдые частицы. Для предотвращения закупорки пор такую суспензию предварительно сгущают в отстойниках. Осадки на фильтровальной перегородке делятся на: 1) сжимаемые, частицы которых деформируются с повышением давления и пористость их уменьшается. К ним относятся осадки гидратов окиси металлов алюминия, железа, меди; 2) несжимаемые, пористость которых не меняется с увеличением давления. К ним относят осадки, состоящие из частиц песка, кристаллов карбоната кальция. В производстве под фильтрованием понимают не только операцию разделения суспензий на фильтрат и осадок, но и последующие операции – промывка, продувка, просушка осадка на фильтре. Скорость фильтрования прямо пропорциональна разности давлений и обратно пропорциональна вязкости жидкости и общему гидравлическому сопротивлению слоя осадка и фильтровальной перегородки.

Так как в процессе фильтрования увеличивается гидравлическое сопротивление слоя осадка с течением времени, то переменную скорость фильтрования выражают в дифференциальной форме:

.

где V — объем фильтрата; F — поверхность фильтрования; — продолжительность фильтрования; Roс — сопротивление слоя осадка; R — сопротивление фильтровальной перегородки.

Основные конструкции фильтров

По способу действия фильтры делятся на аппараты периодического и непрерывного действия; по назначению – фильтры для разделения суспензий и фильтры для очистки воздуха и промышленных газов. В качестве фильтровальной перегородки применяют: ткань, песок; уголь (зернистая перегородка); металлическую сетку; пористую керамику (жесткая перегородка) и др. Самые простые и широко используемые в промышленности нутч или друк – фильтры (аппараты периодического действия), а также дисковые, песочные, патронные, рамные, камерные фильтры. К фильтрам непрерывного действия относятся: вакуумные, барабанные, ленточные, карусельные и др.

Нутч – фильтры работают под вакуумом или под избыточным давлением.

Рис. 2.15. Открытый нутч-фильтр, работающий под вакуумом:

1 — корпус; 2 — суспензия;

3 — фильтровальная перегородка;

4 – пористая подложка; 5 — штуцер для выхода фильтрата, соединенный с

Рис. 2.16. Закрытый нутч–фильтр:

1 — корпус; 2 — обогревающая

рубашка; 3 — кольцевая

перегородка; 4-откидывающееся дно; 5 — фильтровальная перегородка; 6 — опорная решетка;

7 — сетка; 8 — съемная крышка;

9 — предохранительный клапан.

При работе вакуумного нутч – фильтра (рис. 2.15) фильтрация осуществляется путем создания пониженного давления под фильтровальной перегородкой. Осадок удаляется сверху вручную.

Нутч, работающий при избыточном давлении сжатого воздуха (рис. 2.16) имеет более удобное приспособление для удаления осадка, который снимается вручную с фильтровальной перегородки при опускании и повороте дна фильтра. Громоздкость и ручная выгрузка осадка не позволяют использовать эти аппараты очень широко.

Распространенным фильтром периодического действия, работающим под избыточным давлением, является рамный фильтр–пресс (рис. 2.17). Фильтр состоит из чередующихся плит и рам, между которыми зажимается фильтровальная ткань. Плиты имеют по краям гладкую поверхность, а в середине – рифленую (рис. 2.18).

Рис. 2.18. Плита (а), рама (б) и сборка (в) рамного фильтр-пресса:

1 — отверстия в плитах и рамах, образующие при сборке канал для подачи суспензии; 2 — отверстия в плитах и рамах, образующие канал для подачи промывной жидкости; 3 — отводы для прохода суспензии внутрь рам; 4 — внутренние пространства рам; 5 — фильтровальные перегородки; 6 — рифления плит; 7 — каналы в плитах для выхода фильтрата на стадии фильтрования или промывной жидкости — на стадии промывки осадка; 8 — центральные каналы в плитах для сбора фильтрата или промывной жидкости; 9 — краны на линиях вывода фильтрата или промывной жидкости

Рис. 2.17. Схема рамного фильтр-пресса:

1 — упорная плита; 2 — рама; 3 — плита; 4 — фильтрующая ткань; 5 – подвижная концевая плита; 6 — горизонтальная направляющая; 7 — зажимной винт; 8 — станина; 9 — желоб для сбора фильтрата или промывающей жидкости

Полая рама фильтр–пресса помещается между двумя плитами, образуя камеру 4 для осадка. Отверстия 1 и 2 в плитах и рамах совпадают, образуя каналы для прохода соответственно суспензии и промывной воды. Между плитами и рамами помещают фильтровальные перегородки («салфетки»), отверстия в которых совпадают с отверстиями в плитах и рамах. Сжатие плит и рам производится посредством винтового или гидравлического зажимов. Суспензия под давлением нагнетается по каналу 1 и отводам 3 в полое пространство (камеру) внутри рам. Жидкая фаза суспензии проходит через фильтровальные перегородки 5, по желобкам рифлений 6 движется к каналам 7 и далее в каналы 8, которые открыты на стадии фильтрования у всех плит. Когда пространство (камера) 4 заполнится осадком, подачу суспензии прекращают, и начинается промывка осадка. В стадии промывки по боковым каналам 2 подают промывную жидкость, которая омывает осадок и фильтровальные перегородки и выводится через краны 9. По окончании промывки осадок продувают сжатым воздухом и затем раздвигают плиты и рамы. Осадок частично падает в сборник, установленный под фильтром, а оставшаяся часть осадка выгружается вручную. Салфетки при необходимости заменяют.

Рис. 2.19. Схема барабанного вакуум-фильтра:

1 — перфорированный барабан; 2 — волнистая сетка; 3 — фильтрованная перегородка;

4 — осадок; 5 — нож для съема осадка; 6 — корыто для суспензии; 7 — качающаяся мешалка; 8 — устройство для подвода промывной жидкости; 9 — камеры (ячейки) барабана;

10 — соединительные трубки; 11 — вращающаяся часть распределительной головки;

12 — неподвижная часть распределительной головки; I — зона фильтрования и отсоса фильтрата; II — зона промывки осадка и отсоса промывных вод; III — зона съема осадка; IV — зона очистки фильтровальной ткани

Среди фильтров непрерывного действия наиболее распространены барабанные вакуум–фильтры (рис. 2.19). Фильтр имеет вращающийся цилиндрический перфорированный барабан 1, покрытый металлической волнистой сеткой 2, на которой располагается фильтровальная ткань. Барабан на% погружен в суспензию и разделен радиальными перегородками на ряд камер 9. Каждая камера соединяется трубой 10 с различными полостями неподвижной части 12 распределительной головки. Трубы объединяются во вращающуюся часть 11 распределительной головки. Благодаря этому при вращении барабана 1 камеры 9 в определенной последовательности присоединяются к источникам вакуума и сжатого воздуха. При полном обороте барабана каждая камера проходит несколько зон.

Зона I – фильтрования и отсоса фильтрата соприкасается с суспензией и соединена с источником вакуума. Под действием вакуума фильтрат проходит внутрь камеры и через трубу выводится из аппарата, а на фильтровальной ткани остается осадок 4.

Зона II – промывки осадка и отсоса промывных вод также сообщается с вакуумом, а на осадок с помощью устройства 8 подается промывная жидкость. Она проходит через осадок и по трубе выводится из аппарата.

Зона III – съема осадка. Здесь осадок сначала подсушивается за счет вакуума, а затем камера соединяется с источником сжатого воздуха, который сушит и разрыхляет осадок. При подходе камеры с просушенным осадком к ножу 5 подача сжатого воздуха прекращается и осадок падает с поверхности ткани.

🌟 Видео

Закон БернуллиСкачать

Ламинарное и турбулентное теченияСкачать

Гидродинамика НачалоСкачать

Галилео. Эксперимент. Закон БернуллиСкачать

Физика. 10 класс. Гидродинамика. Ламинарное и турбулентное течения жидкостей и газов /26.10.2020/Скачать

Про эффект Ушеренко, бронепробитие и число РейнольдсаСкачать

Дистанционное практическое занятие по разделу "Гидродинамика".Скачать