- Теплоотдача при вынужденном течении жидкости в трубах и каналах
- Теплоотдача при ламинарном течении в трубах и каналах
- Теплоотдача в трубах и каналах при турбулентном режиме
- Расчет теплоотдачи при вынужденной конвекции
- Теплоотдача при свободной конвекции в трубах и каналах
- Свободная конвекция в неограниченном пространстве
- Свободная конвекция в ограниченном объеме
- Расчет теплоотдачи при свободной конвекции
- Критериальные уравнения КТО. Свободная и вынужденная конвекция.
- 10.4. Критериальные уравнения конвективного теплообмена
- 📸 Видео
Видео:Подобие процессов конвективного теплообменаСкачать

Теплоотдача при вынужденном течении жидкости в трубах и каналах
Теплоотдача в трубах и каналах может происходить при вынужденном или свободном характере конвекционных потоков (возможны также их сочетания в случае существенного влияния гравитационных сил).
При вынужденном течении (вынужденная конвекция) жидкость нагнетается или отводится под действием сил внешнего давления, например, ветра, насоса или вентилятора.
Свободное течение жидкости происходит под действием подъемных (гравитационных) сил за счет изменения ее плотности из-за разницы температуры – слой жидкости с меньшей плотностью стремиться занять верхнее положение относительно холодного слоя (свободная или естественная конвекция).
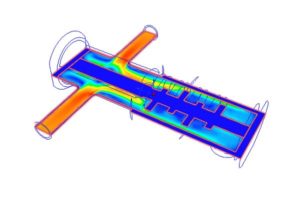
Интенсивность теплоотдачи, как при вынужденной, так и при свободной конвекции характеризуется коэффициентом теплоотдачи α, имеющим размерность Вт/(м 2 ·град), который определяется по формуле:
Nu – число Нуссельта; λ – коэффициент теплопроводности жидкости при средней температуре, Вт/(м·град);
d – эквивалентный диаметр, равный
F – площадь сечения канала, м 2 ; П – периметр канала, м.
Для трубы круглого сечения, эквивалентный диаметр равен внутреннему диаметру трубы.
В целом, расчет коэффициента теплоотдачи сводится к определению числа Нуссельта, значение которого задается соответствующими критериальными уравнениями конвективного теплообмена, зависящими от режима течения жидкости и формы канала.
Течение жидкости в трубах определяется значением числа Рейнольдса Re и в зависимости от его величины может быть ламинарным, переходным или турбулентным.
- Ламинарный режим течения жидкости характеризуется величиной числа Re до 2300.
- При значении числа Re от 2300 до 10000 режим течения в трубах является переходным.
- Турбулентный режим течения в трубах наблюдается при числах Re более 10000.
Число (критерий) Рейнольдса представляет собой безразмерный комплекс, связывающий скоростные и вязкостные характеристики жидкости с определяющим размером канала (для трубы – это ее диаметр).
Число Re определяется по формуле:
w – скорость течения жидкости, м/с; d – эквивалентный диаметр канала, м; ν — кинематическая вязкость жидкости при средней температуре, м 2 /с.
Теплоотдача в трубах и каналах существенно зависит от режима течения жидкости. При ламинарном режиме интенсивность теплоотдачи значительно меньше, чем при развитом турбулентном.
Теплоотдача при ламинарном течении в трубах и каналах
Ламинарный режим течения жидкости обычно характеризуется низкой скоростью потока. При этом в некоторых случаях влиянием конвекции, обусловленной действием гравитационных сил, пренебрегать нельзя.
Для выбора правильного критериального уравнения теплообмена и оценки влияния естественной конвекции на интенсивность теплопередачи при ламинарном режиме служит критерий Грасгофа Gr.
g – ускорение свободного падения, м/с 2 ;
β – температурный коэффициент объемного расширения, град -1 ;
d – эквивалентный диаметр канала, м;
ν — кинематическая вязкость жидкости при средней температуре, м 2 /с;
Δt – средняя разность температур жидкости и стенки, °С.
Теплоотдача при ламинарном течении в трубах и каналах с учетом естественной конвекции. Если величина комплекса GrPr превышает 8·10 5 , то расчет коэффициента теплоотдачи необходимо проводить с учетом влияния естественной конвекции в потоке жидкости по следующему критериальному уравнению:
Индекс «ж» означает, что свойства среды, входящие в критерии подобия Re, Pr и Gr берутся при средней температуре жидкости.
Число Прандтля с индексом «с» Prс берется для жидкости при температуре стенки.
εL – коэффициент, учитывающий изменение теплоотдачи по длине трубы или канала. Его можно определить с помощью таблицы:
| L/d | 1 | 2 | 5 | 10 | 15 | 20 | 30 | 40 | 50 |
|---|---|---|---|---|---|---|---|---|---|
| εL | 1,9 | 1,7 | 1,44 | 1,28 | 1,18 | 1,13 | 1,05 | 1,02 | 1 |
Теплоотдача при ламинарном течении в трубах и каналах без учета естественной конвекции. При значении GrPr 5 , влияние естественной конвекции на теплоотдачу жидкости пренебрежительно мало, и расчет коэффициента теплоотдачи можно проводить по следующему критериальному уравнению:
d – эквивалентный диаметр канала, м;
L – длина трубы (канала), м.
Представленные критериальные уравнения теплообмена при ламинарном режиме позволяют определить среднее значение числа Нуссельта, по величине которого можно рассчитать средний коэффициент теплоотдачи:
λ – коэффициент теплопроводности жидкости при средней температуре, Вт/(м·град);
d – эквивалентный диаметр, м.
Теплоотдача в трубах и каналах при турбулентном режиме
Теплоотдача в трубах и каналах при турбулентном режиме осуществляется путем передачи тепла при интенсивном перемешивании слоев жидкости. Критериальное уравнение теплообмена для расчета средней теплоотдачи в трубах и каналах в этом случае имеет вид:
Критерии подобия Re и Pr берутся при средней температуре жидкости. Число Прандтля с индексом «с» Prс берется при температуре стенки.
Представленное критериальное уравнение применяется в диапазоне чисел Re от 1·10 4 до 5·10 6 и Pr от 0,6 до 2500.
εL – коэффициент, учитывающий изменение среднего коэффициента теплоотдачи по длине трубы или канала при турбулентном режиме течения. Значения εL приведены в следующей таблице при различных числах Рейнольдса и отношениях длины канала к его эквивалентному диаметру:
| Reж | L/d | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 5 | 10 | 15 | 20 | 30 | 40 | 50 | |
| 1·10 4 | 1,65 | 1,5 | 1,34 | 1,23 | 1,17 | 1,13 | 1,07 | 1,03 | 1 |
| 2·10 4 | 1,51 | 1,4 | 1,27 | 1,18 | 1,13 | 1,1 | 1,05 | 1,02 | 1 |
| 5·10 4 | 1,34 | 1,27 | 1,18 | 1,13 | 1,1 | 1,08 | 1,04 | 1,02 | 1 |
| 1·10 5 | 1,28 | 1,22 | 1,15 | 1,1 | 1,08 | 1,06 | 1,03 | 1,02 | 1 |
| 1·10 6 | 1,14 | 1,11 | 1,08 | 1,05 | 1,04 | 1,03 | 1,02 | 1,01 | 1 |
Расчет теплоотдачи в изогнутых трубах и каналах проводится по тому же критериальному уравнению с добавлением множителя — поправки на действие центробежных сил, которая определяется по формуле:
R — радиус изгиба трубы или канала, м; d – эквивалентный диаметр трубы или канала, м.
Теплоотдача в изогнутых трубах проходит более интенсивно, чем в прямых, за счет большего вихреобразования и лучшего перемешивания жидкости.
Расчет теплоотдачи при вынужденной конвекции
Пример расчета. Рассчитаем средний коэффициент теплоотдачи воды, текущей по трубопроводу длиной 1 м, диаметром d=0,01 м с расходом Q=20 л/мин. Средняя температура воды tж=50°С, температура стенки трубы tс=10°С.
1. Определим физические свойства воды при температуре 50°С:
- Теплопроводность воды λж= 0,648 Вт/(м·град);
- Плотность воды ρж=988 кг/м 3 ;
- Кинематическая вязкость воды νж=0,556·10 -6 , м 2 /с;
- Число Прандтля при температуре жидкости Prж=3,54;
- Число Прандтля при температуре стенки Prс=9,52.
2. Рассчитаем среднюю скорость течения воды w по трубе:
3. Определим число Рейнольдса Re:
4. Поскольку число Рейнольдса имеет значение больше 1·10 4 , то режим течения является турбулентным и расчет теплоотдачи необходимо проводить по следующему критериальному уравнению:
Определим коэффициент εL по соотношению L/d=1/0,01=100. Поскольку L/d>50, то коэффициент εL=1.
Выполним расчет числа Нуссельта по приведенному критериальному уравнению:
5. Рассчитаем средний коэффициент теплоотдачи от воды к стенке трубы по формуле:
Таким образом, средний коэффициент теплоотдачи от воды к стенке трубы составляет 14,65 кВт/(м 2 ·град).
Видео:Методы исследования технологических процессов. Теория подобия. Виды подобияСкачать

Теплоотдача при свободной конвекции в трубах и каналах
Теплообмен при свободном движении жидкости (или газа) происходит вследствие разности плотностей нагретых и холодных ее слоев. Интенсивность теплоотдачи жидкости в трубах и каналах при свободной конвекции существенно зависит от их положения в пространстве относительно силы тяжести.
Теплоотдача при свободной конвекции имеет различный характер в случаях свободного течения в неограниченном пространстве и теплообмена в ограниченном объеме (в узкой трубе или канале).
Свободная конвекция в неограниченном пространстве
Конвекция в неограниченном пространстве протекает, например при охлаждении трубопровода центрального отопления, расположенного на улице в безветренную погоду, вблизи от которого отсутствуют препятствия для движения воздушных потоков.
Горизонтальный канал или труба. Интенсивность теплоотдачи при свободной конвекции зависит от величины комплекса GrPr. При значении GrPr от 10 3 до 10 9 критериальное уравнение, описывающее среднюю теплоотдачу от поверхности горизонтальных труб и каналов, имеет вид:
В качестве определяющего размера принимается наружный диаметр d канала или трубы.
Вертикальный канал (труба, пластина). Для вертикальных труб и каналов при значении GrPr от 10 3 до 10 9 критериальное уравнение, описывающее среднюю теплоотдачу, имеет вид:
При GrPr>10 9 :
Примечание: В приведенных критериальных уравнениях теплообмена свойства жидкости, входящие в числа Gr и Pr, определяются при температуре окружающей среды. Число Прандтля с индексом «с» Prс берется для жидкости при температуре стенки. В качестве определяющего размера принимается длина L (высота) вертикально стоящей трубы или канала.
Свободная конвекция в ограниченном объеме
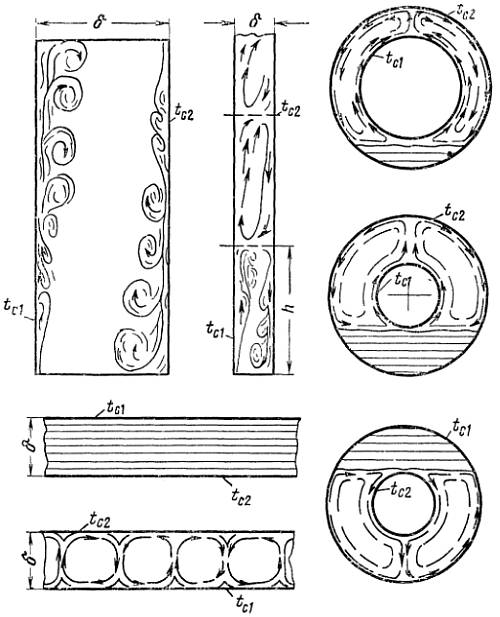
Теплообмен жидкости в ограниченном объеме при свободной конвекции характеризуется совместным протеканием процессов нагрева и охлаждения соседних слоев жидкости (или газа). Эти процессы сопровождаются сложным течением нисходящих и восходящих потоков, зависящих от рода жидкости, разницы температуры, формы канала и его геометрических размеров.
Для упрощения расчета таких сложных процессов конвективного теплообмена принято рассматривать их, как явление теплопроводности в щели толщиной δ с учетом понятия эквивалентного коэффициента теплопроводности λэк.
Эквивалентный коэффициент теплопроводности определяется по формуле:
Q — количество переданного тепла, Вт; δ — толщина слоя жидкости (или газа), м; F — площадь теплоотдающей поверхности, м 2 ; Δt=tc1-tc2 — температурный напор между нагретой и холодной стенками, °С.
Отношение эквивалентного коэффициента теплопроводности λэк к величине теплопроводности окружающей жидкости при средней температуре называется коэффициентом конвекции εк, который определяется значением комплекса GrPr.
При малых значениях комплекса GrPr 3 6 :
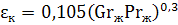
Примечание: Числа подобия Gr и Pr рассчитываются при средней температуре жидкости (или газа), равной tж=0,5(tc1+tc2). В качестве определяющего размера принимается δ — толщина слоя жидкости.
Расчет теплоотдачи при свободной конвекции
Пример расчета. Рассчитаем потери тепла естественной конвекцией от горизонтального трубопровода центрального отопления, находящегося на открытом воздухе. Диаметр трубопровода d=0,15 м, длина L=5 м, средняя температура наружной стенки tс=80°С. Температура окружающего воздуха tж=20°С.
1. Определим физические свойства воздуха при температуре 20°С:
- Теплопроводность воздуха λж= 0,0259 Вт/(м·град);
- Кинематическая вязкость воздуха νж=15,06·10 -6 , м 2 /с;
- Число Прандтля при температуре жидкости Prж=0,703;
- Число Прандтля при температуре стенки Prс=0,69;
- Коэффициент объемного расширения βж=1/(273+20)=0,00341 град -1 .
2. Вычислим число Грасгофа Gr по формуле:
3. Определим значение комплекса GrPr:
Этому значению комплекса соответствует следующее критериальное уравнение теплообмена при свободной конвекции в случае горизонтальной трубы:
4. Вычислим значение числа Нуссельта Nu:
5. Рассчитаем коэффициент теплоотдачи от трубы α по формуле:
6. Определим потери тепла с боковой поверхности трубопровода по формуле:
Подставляя численные значения, окончательно получаем потерю тепла:
Таким образом, только путем естественной (свободной) конвекции рассмотренный трубопровод отопления отдает воздуху 1681 Вт тепла.
Видео:Л2 - Конвективный теплообмен.Скачать

Критериальные уравнения КТО. Свободная и вынужденная конвекция.
Читайте также:
|
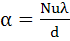
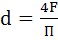
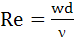
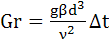
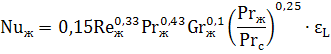
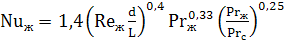
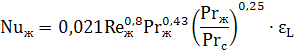
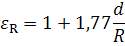
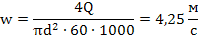
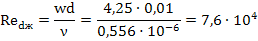

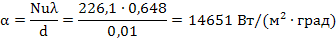
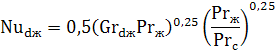
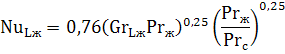
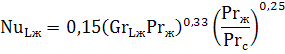
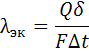
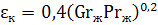
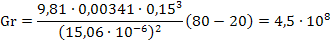
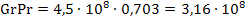
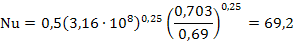
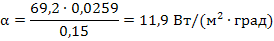
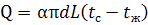
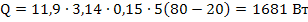
 Q = QA + QD + QB
Q = QA + QD + QB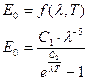 λ – длина волны, Т – абсолютная температура, С1, С2 – константы.
λ – длина волны, Т – абсолютная температура, С1, С2 – константы.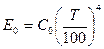 — для чёрного тела,
— для чёрного тела,  — для серого тела. ε – степень черноты.
— для серого тела. ε – степень черноты. .
. . При условии установления экрана с ε как у 1 и 2 поверхности, тепловой поток излучения уменьшится в 2 раза. Если будут 2,3,…,n экранов, тепловой поток будет уменьшаться в
. При условии установления экрана с ε как у 1 и 2 поверхности, тепловой поток излучения уменьшится в 2 раза. Если будут 2,3,…,n экранов, тепловой поток будет уменьшаться в  раз.
раз. .
. Н2О
Н2О 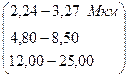
 Pl – сила поглощ.
Pl – сила поглощ. , где f – среда газообразная, W – стенка, εW ’ – приведена степень черноты поверхности стенки.
, где f – среда газообразная, W – стенка, εW ’ – приведена степень черноты поверхности стенки. ,
,  — степень черноты газа.
— степень черноты газа. — газа,
— газа,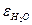 — водяного пара.
— водяного пара. .
.















