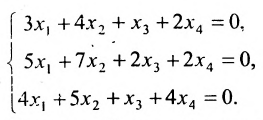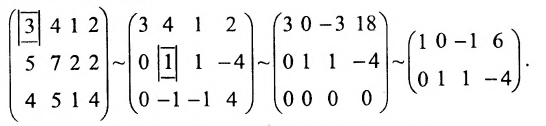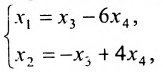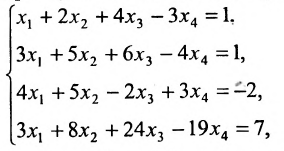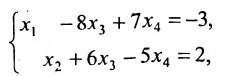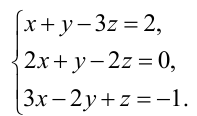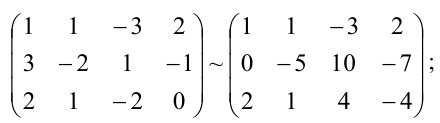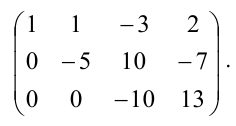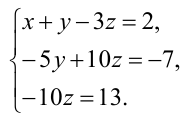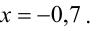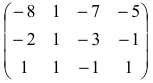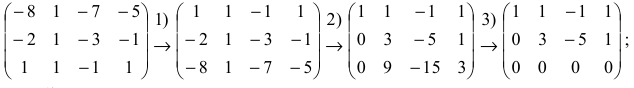Тема 2. Системы линейных уравнений
Критерий совместности систем линейных уравнений
Система m линейных уравнений c n неизвестными имеет вид:
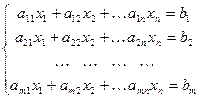
Здесь 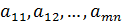

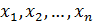
где A = (аij) — матрица, состоящая из коэффициентов при неизвестных системы (2.1), которая называется матрицей системы, X = (x1, x2. xn) T ,
B = (b1, b2. bm) T — векторы-столбцы, составленные соответственно из неизвестных xj и из свободных членов bi.
Система называется однородной, если все ее свободные члены равны нулю: bi=0 для всех i.
Если хотя бы один из свободных членов отличен от нуля, система называется неоднородной.
Совокупность 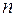
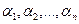
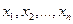
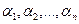
Система (2.1) называется совместной, или разрешимой, если она имеет по крайней мере одно решение. Система называется несовместной, или неразрешимой, если она не имеет решений.
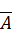
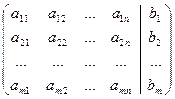
образованная путем приписывания справа к матрице 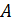
Теорема Кронекера- Капелли. Система линейных уравнений (2.1) совместна тогда и только тогда, когда ранги матриц 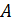
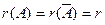
Для множества решений системы (2.1) имеются три возможности:
1) Если 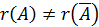
2) Если 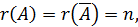
3) Если 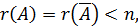
Рассмотрим более подробно случай неопределенной системы. Предположим, что базисный минор матрицы находится в левом верхнем углу расширенной матрицы (всегда можно перенумеровать неизвестные и поменять местами строки, чтобы это было верно). Если ранг расширенной матрицы системы равен r, то первые r ее строк являются базисными. По теореме о базисном миноре каждая из строк расширенной матрицы, начиная с (r+1)-ой строки, является линейной комбинацией первых r строк этой матрицы. Это означает, что каждое из уравнений системы (2.1), начиная с (r+1)-го уравнения, является линейной комбинацией первых r уравнений этой системы. Придавая неизвестным 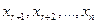

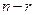
Универсальным методом решения систем линейных уравнений является метод Гаусса, или метод исключения неизвестных. В частном случае, когда матрица системы 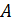
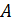
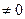
Пример 2.1. Исследовать систему уравнений на совместность:
Решение.Выписываем расширенную матрицу системы:
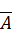
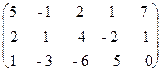
Вычислим ранг основной матрицы системы. Очевидно, что, например, минор второго порядка в левом верхнем углу 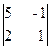
M¢3 = 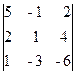
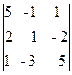
Следовательно, ранг основной матрицы системы равен 2, т.е. r(A)=2. Для вычисления ранга расширенной матрицы `A рассмотрим окаймляющий минор
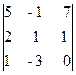

значит, ранг расширенной матрицы r( 
Дата добавления: 2015-09-29 ; просмотров: 3037 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
- Метод Гаусса — определение и вычисление с примерами решения
- Алгоритм решения системы m линейных уравнений с n неизвестными методом Гаусса
- Исследование совместности и определённости системы. Теорема Кронекера-Капелли
- Однородные системы линейных уравнений
- Фундаментальная система решений. Общее решение неоднородной системы линейных уравнений
- Определение метода Гаусса
- Вычисление метода Гаусса
- Метод Крамера – теорема, примеры решений
- Вывод формулы Крамера
- Метод Крамера – теоремы
- Теорема замещения
- Теорема аннулирования
- Алгоритм решения уравнений методом Крамера
- Шаг 1. Вычисляем главный определитель матрицы
- Шаг 2. Находим определители
- Шаг 3. Вычисляем неизвестные переменные
- Шаг 4. Выполняем проверку
- Порядок решения однородной системы уравнений
- Примеры решения методом Крамера
- Подведём итоги
- 🎬 Видео
Видео:Исследование систем линейных уравнений на совместностьСкачать

Метод Гаусса — определение и вычисление с примерами решения
Содержание:
Базисные и свободные переменные:
Пусть задана система
Элементарными преобразованиями системы линейных уравнений называются следующие преобразования:
- исключение из системы уравнения вида
- умножение обеих частей одного из уравнений системы на любое действительное число
;
- перестановка местами уравнений системы;
- прибавление к обеим частям одного из уравнений системы соответствующих частей другого уравнения, умноженных на любое действительное число не равное нулю.
Элементарные преобразования преобразуют данную систему уравнений в эквивалентную систему, т.е. в систему, которая имеет те же решения, что и исходная.
Для решения системы т линейных уравнений с т неизвестными удобно применять метод Гаусса, называемый методом последовательного исключения неизвестных, который основан на применении элементарных преобразований системы. Рассмотрим этот метод.
Предположим, что в системе (6.1.1)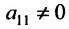
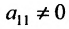
На первом шаге метода Гаусса исключим неизвестное 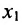
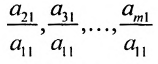
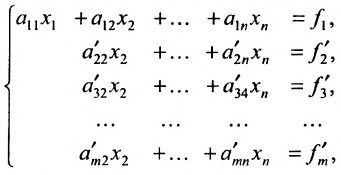
в которой коэффициенты 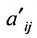
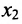
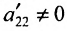
чтобы это условие было выполнено). Для исключения неизвестного 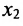
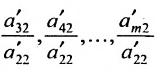
в которой коэффициенты 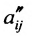
Продолжая аналогичные преобразования, систему (6.1.1) можно привести к одному из видов:
Совокупность элементарных преобразований, приводящих систему (6.1.1) к виду (6.1.4) или (6.1.5) называется прямым ходом метода Гаусса.
Отметим, что если на каком-то шаге прямого хода метода Гаусса получим уравнение вида:
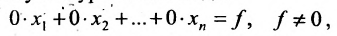
Итак, предположим, что в результате прямого хода метода Гаусса мы получили систему (6.1.4), которая называется системой треугольного вида. Тогда из последнего уравнения находим значение 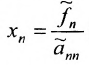
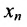
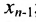
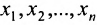
Если же в результате прямого хода метода Гаусса мы получим систему (6.1.5), которая называется системой ступенчатого вида, то из последнего уравнения этой системы находим значение неизвсстного 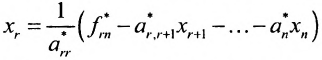
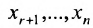
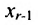
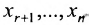
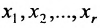
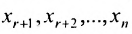
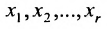
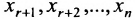
Таким образом, если система (6.1.1) путём элементарных преобразований приводится к треугольному виду (6.1.4), то она имеет единственное решение, если же она приводится к системе ступенчатого вида (6.1.5), то она имеет бесконечное множество решений. При этом неизвестные 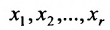
Практически удобнее преобразовывать не саму систему уравнений (6.1.1), а расширенную матрицу системы, соединяя последовательно получающиеся матрицы знаком эквивалентности
Формализовать метод Гаусса можно при помощи следующего алгоритма.
Видео:Лекция 13. Исследование систем линейных уравнений. Теорема Кронекера — Капелли.Скачать

Алгоритм решения системы m линейных уравнений с n неизвестными методом Гаусса
1. Составьте расширенную матрицу коэффициентов системы уравнений так, чтобы 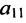
2. Выполните первый шаг метода Гаусса: в первом столбце начиная со второй строки, запишите нули, а все другие элементы вычислите по формуле
Матрица после первого шага примет вид
3. Выполните второй шаг метода Гаусса, предполагая, что 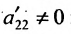
После второго шага матрица примет вид
4. Продолжая аналогичные преобразования, придёте к одному из двух случаев:
а) либо в ходе преобразований получим уравнение вида
тогда данная система несовместна;
б) либо придём к матрице вида:
где 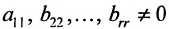
связано с тем, что в процессе преобразований матрицы исключаются строки, состоящие из нулей.
5. Использовав конечную матрицу, составьте систему, при этом возможны два случая:
Система имеет единственное,решение 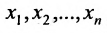
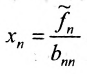
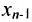
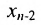
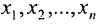
5.2. 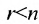
Тогда r неизвестных будут базисными, а остальные (n-r) — свободными. Из последнего уравнения выражаете неизвестное 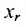
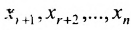
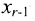
Система имеет в этом случае бесконечное множество решений.
Приведенный алгоритм можно несколько видоизменить и получить алгоритм полного исключения, состоящий в выполнении следующих шагов. На первом шаге:
- составляется расширенная матрица;
- выбирается разрешающий элемент расширенной матрицы
(если
, строки матрицы можно переставить так, чтобы выполнялось условие
);
- элементы разрешающей строки (строки, содержащей разрешающий элемент) оставляем без изменения; элементы разрешающего столбца (столбца, содержащего разрешающий элемент), кроме разрешающего элемента, заменяем нулями;
- все другие элементы вычисляем по правилу прямоугольника: преобразуемый элемент равен разности произведений элементов главной диагонали (главную диагональ образует разрешающий элемент и преобразуемый) и побочной диагонали (побочную диагональ образуют элементы, стоящие в разрешающей строке и разрешающем столбце):
— разрешающий элемент (см. схему).
Последующие шаги выполняем по правилам:
1) выбирается разрешающий элемент 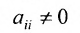
2) элементы разрешающей строки оставляем без изменения;
3) все элементы разрешающего столбца, кроме разрешающего элемента, заменяем нулями; • •
4) все другие элементы матрицы пересчитываем по правилу прямоугольника.
На последнем шаге делим элементы строк на диагональные элементы матрицы, записанные слева от вертикальной черты, и получаем решение системы.
Пример:
Решить систему уравнений:
Решение:
Составим расширенную матрицу системы, и применим алгоритм полного исключения, обозначая разрешающий элемент символом
Из последней матрицы находим следующее решение системы
уравнении:
Ответ:
Пример:
Решить систему уравнений:
Решение:
Составим расширенную матрицу системы, и применим алгоритм полного исключения, обозначая разрешающий элемент символом
Система привелась к ступенчатому виду (трапециевидной форме):
в которой неизвестные 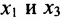
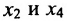
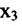
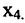
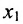
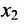
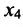
в котором 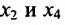
Если в общем решении положить 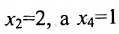
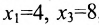
Ответ: система имеет бесконечное множество решений, общее решение которой записывается в виде:
Пример:
Решить систему уравнений:
Решение:
Составим расширенную матрицу системы, и применим алгоритм полного исключения, обозначая разрешающий элемент символом 
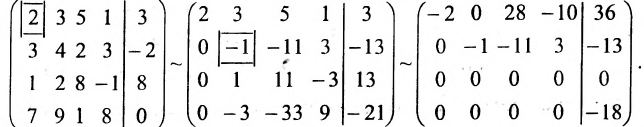
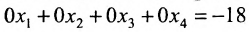
Ответ: система несовместна.
Замечание 1. Если дана система уравнений (6.1.1), в которой число уравнений m равно числу неизвестных n (m=n) и определитель этой системы 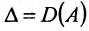
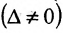
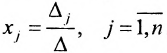
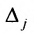
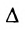
Если же такую систему (m-n) записать в матричной форме AX=F, то её решение можно найти по формуле 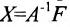
Замечание 2. Используя метод Гаусса, тем самым и алгоритм полного исключения, можно находить обратную матрицу. Для этого составляется расширенная матрица, в которой слева от вертикальной черты записана матрица А, а справа — единичная матрица. Реализовав алгоритм полного исключения, справа от вертикальной черты получаем обратную матрицу, а слева — единичную.
Пример:
Найти обратную матрицу для матрицы:
Решение:
то обратная матрица 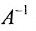
Покажем, что
ответ
Исследование совместности и определённости системы. Теорема Кронекера-Капелли
Рассмотрим систему (6.1.1) m линейных уравнений с n неизвестными при любых m и n (случай m=n не исключается). Вопрос о совместности системы решается следующим критерием.
Теорема 6.2.1. (критерий Кронкера-Капелли). Для того, чтобы система линейных уравнений(6.1.1) была совместна, необходимо и достаточно, чтобы ранг матрицы А системы был равен рангу расширенной матрицы 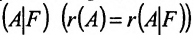
Доказательство и Необходимость:
Предположим, что система (6.1.1) совместна и 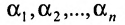
Из этих равенств следует, что последний столбец матрицы 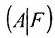
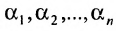
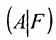
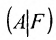
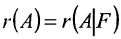
Достаточность. Пусть 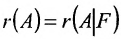
столбцов матрицы А, которые одновременно будут базисными столбцами и матрицы 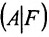
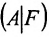
где 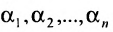
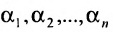
эта система совместна.
Совместная система линейных уравнений (6.1.1) может быть либо определенной, либо неопределенной.
Следующая теорема даст критерий определенности.
Теорема 6.2.2. Совместная система линейных уравнений имеет единственное решение тогда и только тогда, когда ранг матрицы А системы равен числу п ее неизвестных.
Таким образом, если число уравнений m системы (6.1.1) меньше числа ее неизвестных n и система совместна, то ранг матрицы системы 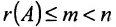
В случае 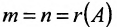
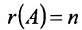
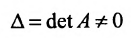
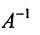
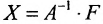
Следует отметить, что, решая систему (6.1.1) методом Гаусса, мы определяем и совместность, и определённость системы.
Пример:
Исследовать на совместность и определённость следующую систему линейных уравнений:
Решение:
Составим расширенную матрицу заданной системы. Определяя её ранг, находим тем самым и ранг матрицы системы. Для нахождения ранга матрицы применим алгоритм метода Гаусса.
Из последней матрицы следует, что ранг расширенной матрицы 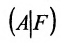
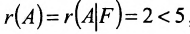
Однородные системы линейных уравнений
Система линейных уравнений (6.1.1) называется однородной, если все свободные члены 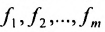
Эта система всегда совместна, так как очевидно, что она имеет нулевое решение
Для однородной системы важно установить, имеет ли она ненулевые решения. Этот факт устанавливается следующей теоремой.
Теорема 6.3.1. Для того, чтобы однородная система имела ненулевые решения, необходимо и достаточно, чтобы ранг г матрицы А системы был меньше числа неизвестных n (r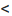
Доказательство. Необходимость. Пусть система (6.3.1) имеет ненулевое решение. Тогда она неопределённая, т.к. имеет еще и нулевое решение. В силу теоремы 6.2.2 ранг матрицы неопределённой системы не может равняться n потому что при r(А)=n система определённая. Следовательно, 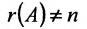
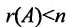
Достаточность. Если 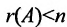
Следствие 1. Если число неизвестных в однородной системе больше числа уравнений, то однородная система имеет ненулевые решения.
Доказательство. Действительно, ранг матрицы системы (6.3.1) не может превышать m. Но так как по условию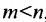
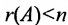
Следствие 2. Для того, чтобы однородная система с квадрат-ной матрицей имела ненулевые решения, необходимо и достаточно, чтобы её определитель 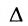
Доказательство. Рассмотрим однородную систему с квадратной матрицей:
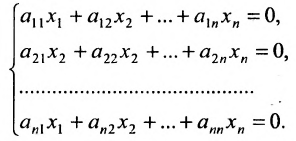
Если определитель матрицы системы 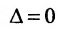
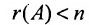
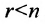
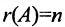
Пример:
Решить систему однородных линейных уравнений:
Решение:
Составим матицу системы и применим алгоритм полного исключения:
Из последней матрицы следует, что 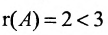
Используя последнюю матрицу, последовательно находим общее решение:
Неизвестные 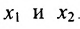
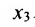
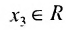
Фундаментальная система решений. Общее решение неоднородной системы линейных уравнений
Рассмотрим систему однородных линейных уравнений
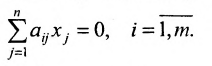
системы m линейных однородных уравнений с n неизвестными можно рассматривать как вектор-строку 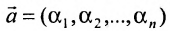
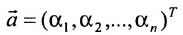
1) сумма двух решений также является решением системы, т.е.
если 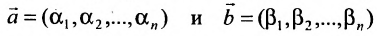
(6.4.1), то и 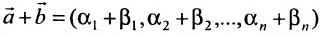
2) произведение решений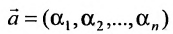
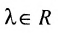
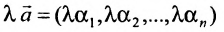
Из приведенных свойств следует, что
3) линейная комбинация решений системы (6.4.1) является решением этой системы.
В частности, если однородная система (6.4.1) имеет хотя бы одно ненулевое решение, то из него умножением на произвольные числа, можно получить бесконечное множество решений.
Определение 6.4.1. Фундаментальной системой решений для системы однородных линейных уравнений (6.4.1) называется линейно независимая система решений, через которую линейно выражается любое решение системы (6.4.1).
Заметим, что если ранг матрицы системы (6.4.1) равен числу неизвестных n (r(А)=n), то эта система не имеет фундаментальной системы решений, так как единственным решением будет нулевое решение, составляющее линейно зависимую систему. Существование и число фундаментальных решений определяется следующей теоремой.
Теорема 6.4.1. Если ранг матрицы однородной системы уравнений (6.4.1) меньше числа неизвестных (r(А)
Сформулируем алгоритм построения фундаментальной системы решений:
- Выбираем любой определитель
порядка n-r, отличный от нуля, в частности, определитель порядка n-r, у которого элементы главной диагонали равны единице, а остальные — нули.
- Свободным неизвестным придаём поочерёдно значения, равные элементам первой, второй и т.д. строк определителя
, и каждый раз из общего решения находим соответствующие значения базисных неизвестных.
- Из полученных n-r решений составляют фундаментальную систему решений.
Меняя произвольно определитель 
Пример:
Найти общее решение и фундаментальную систему решений для однородной системы уравнений:
Решение:
Составим матрицу системы и применим алгоритм полного исключения.
Для последней матрицы составляем систему:
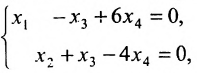
, из которой находим общее решение:
в котором 
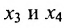
Построим фундаментальную систему решений. Для этого выбираем определитель 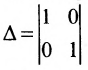
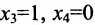
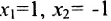
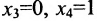
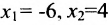
Таким образом, построенные два решения (1; -1; 1; 0) и (-6; 4; 0; 1) составляют фундаментальную систему решений.
Если ранг матрицы системы однородных линейных уравнений (6.4.1) на единицу меньше числа неизвестных: 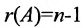
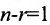
Рассмотрим теперь неоднородную систему m линейных уравнений с n неизвестными (6.1.1). Если в системе (6.1.1) положить 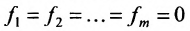
Решения системы (6.1.1) и её приведенной системы удовлетворяют свойствам:
- Сумма и разность любого решения системы (6.1.1) и любого решения её приведенной системы является решением неоднородной системы.
- Все решения неоднородной системы можно получить, прибавляя к одному (любому) её решению поочерёдно все решения её приведенной системы.
Из этих свойств следует теорема.
Теорема 6.4.2. Общее решение неоднородной системы (6.1.1.) определяется суммой любого частного решения этой системы и общего решения её приведенной системы.
Пример:
Найти общее решение системы:
Решение:
Составим расширенную матрицу (A|F) заданной системы и применим алгоритм полного исключения:
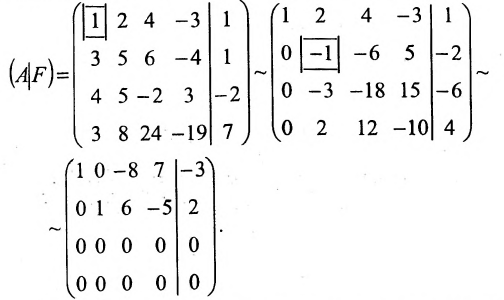
Преобразованной матрице соответствует система уравнений:
из которой находим общее решение системы:
, где 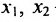
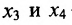
Покажем, что это общее решение определяется суммой любого частного решения заданной системы и общего решения приведенной системы.
Подставляя вместо свободных неизвестных 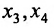
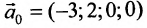
Очевидно, что общее решение приведенной системы имеет вид:
Суммируя частное решение заданной системы и общее решение приведенной системы, получим общее решение (6.4.2) исходной системы.
Отметим, что общее решение системы (6.1.1) можно представить в векторном виде:
где 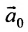
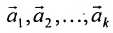
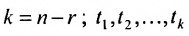
Формула (6.4.4) называется общим решением системы (6.1.1) в векторной форме.
Запишем общее решение системы примера 6.4.1 в векторной форме. Для этого определим фундаментальную систему решений приведенной системы. Возьмём определитель 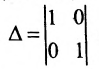
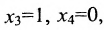
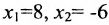
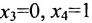
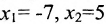
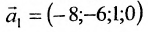
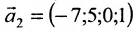
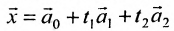
Видео:Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Определение метода Гаусса
Исторически первым, наиболее распространенным методом решения систем линейных уравнений является метод Гаусса, или метод последовательного исключения неизвестных. Сущность этого метода состоит в том, что посредством последовательных исключений неизвестных данная система превращается в ступенчатую (в частности, треугольную) систему, равносильную данной. При практическом решении системы линейных уравнений методом Гаусса удобнее приводить к ступенчатому виду не саму систему уравнений, а расширенную матрицу этой системы, выполняя элементарные преобразования над ее строками. Последовательно получающиеся в ходе преобразования матрицы обычно соединяют знаком эквивалентности.
Пример:
Решить систему уравнений методом Гаусса:
Решение:
Выпишем расширенную матрицу данной системы 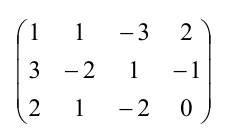
а) из ее второй и третьей строк вычтем первую, умноженную соответственно на 3 и 2:
б) третью строку умножим на (-5) и прибавим к ней вторую:
В результате всех этих преобразований данная система приводится к треугольному виду:
Из последнего уравнения находим 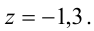
Видео:13 Исследование систем линейных уравненийСкачать

Вычисление метода Гаусса
Этот метод основан на следующей теореме.
Теорема:
Элементарные преобразования не изменяют ранга матрицы.
К элементарным преобразованиям матрицы относят:
- перестановку двух параллельных рядов;
- умножение какого-нибудь ряда на число, отличное от нуля;
- прибавление к какому-либо ряду матрицы другого, параллельного ему ряда, умноженного на произвольное число.
Путем элементарных преобразований исходную матрицу можно привести к трапециевидной форме
где все диагональные элементы 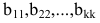
Пример:
Найти ранг матрицы
1) методом окаймляющих миноров;
2 ) методом Гаусса.
Указать один из базисных миноров.
Решение:
1. Найдем ранг матрицы методом окаймляющих миноров. Выберем минор второго порядка, отличный от нуля. Например,
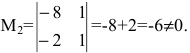
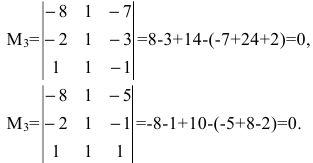
2. Найдем ранг матрицы методом Гаусса. Производя последовательно элементарные преобразования, получим:
- переставили первую и третью строки;
- первую строку умножили на 2 и прибавили ко второй, первую строку умножили на 8 и прибавили к третьей;
- вторую строку умножили на -3 и прибавили к третьей.
Последняя матрица имеет трапециевидную форму и ее ранг равен двум. Следовательно, ранг исходной матрицы также равен двум.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Прямая линия на плоскости и в пространстве
- Плоскость в трехмерном пространстве
- Функция одной переменной
- Производная функции одной переменной
- Дифференциальные уравнения с примерами
- Обратная матрица — определение и нахождение
- Ранг матрицы — определение и вычисление
- Определители второго и третьего порядков и их свойства
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Совместные и несовместные, определенные и неопределенные системы линейных уравненийСкачать

Метод Крамера – теорема, примеры решений
Метод Крамера часто применяется для систем линейных алгебраических уравнений (СЛАУ). Этот способ решения один из самых простых. Как правило, данный метод применяется только для тех систем, где по количеству неизвестных столько же, сколько и уравнений. Чтобы получилось решить уравнение, главный определитель матрицы не должен равняться нулю.
Габриель Крамер – математик, создатель одноименного метода решения систем линейных уравнений
Габриель Крамер – известный математик, который родился 31 июля 1704 года. Ещё в детстве Габриель поражал своими интеллектуальными способностями, особенно в области математики. Когда Крамеру было 20 лет, он устроился в Женевский университет штатным преподавателем.
Во время путешествия по Европе Габриель познакомился с математиком Иоганном Бернулли, который и стал его наставником. Только благодаря Иоганну, Крамер написал много статей по геометрии, истории математики и философии. А в свободное от работы время изучал математику всё больше и больше.
Наконец-то наступил тот день, когда Крамер нашёл способ, при помощи которого можно было бы легко решать не только лёгкие, но и сложные системы линейных уравнений.
В 1740 году у Крамера были опубликованы несколько работ, где доступно изложено решение квадратных матриц и описан алгоритм, как находить обратную матрицу. Далее математик описывал нахождения линейных уравнений разной сложности, где можно применить его формулы. Поэтому тему так и назвали: «Решение систем линейных уравнений методом Крамера».
Учёный умер в возрасте 48 лет (в 1752 году). У него было ещё много планов, но, к сожалению, он так и не успел их осуществить.
Видео:Решение системы уравнений методом ГауссаСкачать

Вывод формулы Крамера
Пусть дана система линейных уравнений такого вида:
где ,
,
– неизвестные переменные,
– это числовые коэффициенты, в
– свободные члены.
Решением СЛАУ (систем линейных алгебраических уравнение) называются такие неизвестные значения при которых все уравнения данной системы преобразовываются в тождества.
Если записать систему в матричном виде, тогда получается , где
В данной главной матрице находятся элементы, коэффициенты которых при неизвестных переменных,
Это матрица-столбец свободных членов, но есть ещё матрица-столбец неизвестных переменных:
После того, когда найдутся неизвестные переменные, матрица и будет решением системы уравнений, а наше равенство
преобразовывается в тождество.
. Если умножить
, тогда
. Получается:
.
Если матрица – невырожденная, то есть, её определитель не равняется нулю, тогда у СЛАУ есть только одно единственное решение, которое находится при помощи метода Крамера.
Как правило, для решения систем линейных уравнений методом Крамера, нужно обращать внимания на два свойства, на которых и основан данный метод:
1. Определитель квадратной матрицы равняется сумме произведений элементов любой из строк (столбца) на их алгебраические дополнения:
, здесь
– 1, 2, …, n;
– 1, 2, 3, …, n.
2. Сумма произведений элементов данной матрицы любой строки или любого столбца на алгебраические дополнения определённых элементов второй строки (столбца) равняется нулю:
,
,
где – 1, 2, …, n;
– 1, 2, 3, …, n.
.
Итак, теперь можно найти первое неизвестное . Для этого необходимо умножить обе части первого уравнения системы на
, части со второго уравнения на
, обе части третьего уравнения на
и т. д. То есть, каждое уравнение одной системы нужно умножать на определённые алгебраические дополнения первого столбца матрицы
:
Теперь прибавим все левые части уравнения, сгруппируем слагаемые, учитывая неизвестные переменные и приравняем эту же сумму к сумме правых частей системы уравнения:
.
Можно обратиться к вышеописанным свойствам определителей и тогда получим:
И предыдущее равенство уже выглядит так:
Откуда и получается .
Аналогично находим . Для этого надо умножить обе части уравнений на алгебраические дополнения, которые находятся во втором столбце матрицы
.
Теперь нужно сложить все уравнения системы и сгруппировать слагаемые при неизвестных переменных. Для этого вспомним свойства определителя:
Откуда получается .
Аналогично находятся все остальные неизвестные переменные.
тогда получаются формулы, благодаря которым находятся неизвестные переменные методом Крамера:
,
,
.
Замечание.
Тривиальное решение при
может быть только в том случае, если система уравнений является однородной
. И действительно, если все свободные члены нулевые, тогда и определители равняются нулю, так как в них содержится столбец с нулевыми элементами. Конечно же, тогда формулы
,
,
дадут
Нужна помощь в написании работы?
Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.
Видео:Система линейных уравнений. Общее решение. Метод ГауссаСкачать

Метод Крамера – теоремы
Прежде чем решать уравнение , необходимо знать:
- теорему аннулирования;
- теорему замещения.
Теорема замещения
Сумма произведений алгебраических дополнений любого столбца (строки) на произвольные числа равняется новому определителю, в котором этими числами заменены соответствующие элементы изначального определителя, что отвечают данным алгебраическим дополнениям.
=
где – алгебраические дополнения элементов
первого столбца изначального определителя:
Теорема аннулирования
Сумма произведений элементов одной строки (столбца) на алгебраические дополнения соответствующих элементов другой строки (столбца) равняется нулю.
Видео:15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

Алгоритм решения уравнений методом Крамера
Метод Крамера – простой способ решения систем линейных алгебраических уравнений. Такой вариант применяется исключительно к СЛАУ, у которых совпадает количество уравнений с количеством неизвестных, а определитель отличен от нуля.
Итак, когда выучили все этапы, можно переходить к самому алгоритму решения уравнений методом Крамера. Запишем его последовательно:
Шаг 1. Вычисляем главный определитель матрицы
и необходимо убедиться, что определитель отличен от нуля (не равен нулю).
Шаг 2. Находим определители
Это и есть определители матриц, которые получались из матрицы при замене столбцов на свободные члены.
Шаг 3. Вычисляем неизвестные переменные
Теперь вспоминаем формулы Крамера, по которым вычисляем корни (неизвестные переменные):
,
,
.
Шаг 4. Выполняем проверку
Выполняем проверку решения при помощи подстановки в исходную СЛАУ. Абсолютно все уравнения в системе должны быть превращены в тождества. Также можно высчитать произведение матриц
. Если в итоге получилась матрица, которая равняется
, тогда система решена правильно. Если же не равняется
, скорей всего в одном из уравнений есть ошибка.
Давайте для начала рассмотрим систему двух линейных уравнений, так как она более простая и поможет понять, как правильно использовать правило Крамера. Если вы поймёте простые и короткие уравнения, тогда сможете решить более сложные системы трёх уравнений с тремя неизвестными.
Кроме всего прочего, есть системы уравнений с двумя переменными, которые решаются исключительно благодаря правилу Крамеру.
Итак, дана система двух линейных уравнений:
Для начала вычисляем главный определитель (определитель системы):
Значит, если , тогда у системы или много решений, или система не имеет решений. В этом случае пользоваться правилом Крамера нет смысла, так как решения не получится и нужно вспоминать метод Гаусса, при помощи которого данный пример решается быстро и легко.
В случае, если , тогда у система есть всего одно решение, но для этого необходимо вычислить ещё два определителя и найти корни системы.
Часто на практике определители могут обозначаться не только , но и латинской буквой
, что тоже будет правильно.
Корни уравнения найти просто, так как главное, знать формулы:
,
Так как мы смогли решить систему двух линейных уравнений, теперь без проблем решим и систему трёх линейных уравнений, а для этого рассмотрим систему:
Здесь алгебраические дополнения элементов – первый столбец . Во время решения не забывайте о дополнительных элементах. Итак, в системе линейных уравнений нужно найти три неизвестных –
при известных других элементах.
Создадим определитель системы из коэффициентов при неизвестных:
Умножим почленно каждое уравнение соответственно на ,
,
– алгебраические дополнения элементов первого столбца (коэффициентов при
) и прибавим все три уравнения. Получаем:
Согласно теореме про раскладывание, коэффициент при равняется
. Коэффициенты при
и
будут равняться нулю по теореме аннулирования. Правая часть равенства по теореме замещения даёт новый определитель, который называется вспомогательным и обозначается
После этого можно записать равенство:
Для нахождения и
перемножим каждое из уравнений изначальной системы в первом случае соответственно на
, во втором – на
и прибавим. Впоследствии преобразований получаем:
,
Если , тогда в результате получаем формулы Крамера:
=
,
=
,
=
Видео:Теорема Кронекера-КапеллиСкачать

Порядок решения однородной системы уравнений
Отдельный случай – это однородные системы:
Среди решений однородной системы могут быть, как нулевые решения , так и решения отличны от нуля.
Если определитель однородной системы (3) отличен от нуля
, тогда у такой системы может быть только одно решение.
Действительно, вспомогательные определители , как такие у которых есть нулевой столбец и поэтому, за формулами Крамера
Если у однородной системы есть отличное от нуля решение, тогда её определитель равняется нулю
Действительно, пусть одно из неизвестных , например, , отличное от нуля. Согласно с однородностью
Равенство (2) запишется:
. Откуда выплывает, что
Видео:Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Примеры решения методом Крамера
Рассмотрим на примере решение методом Крамера и вы увидите, что сложного ничего нет, но будьте предельно внимательно, так как частые ошибки в знаках приводят к неверному ответу.
Задача
Решить систему линейных уравнений методом Крамера:
Решение
Первое, что надо сделать – вычислить определитель матрицы:
Как видим, , поэтому по теореме Крамера система имеет единственное решение (система совместна). Далее нужно вычислять вспомогательные определители. Для этого заменяем первый столбец из определителя
на столбец свободных коэффициентов. Получается:
Аналогично находим остальные определители:
,
.
Ответ
,
.
Задача
Решить систему уравнений методом Крамера:
Решение
Ответ
=
=
=
=
=
=
Проверка
*
=
*
=
=
*
=
*
=
=
*
=
*
=
=
Уравнение имеет единственное решение.
Ответ
=
=
=
Задача
Решить систему методом Крамера
Решение
Как вы понимаете, сначала находим главный определитель:
Как мы видим, главный определитель не равняется нулю и поэтому система имеет единственное решение. Теперь можно вычислить остальные определители:
При помощи формул Крамера находим корни уравнения:
,
,
.
Чтобы убедиться в правильности решения, необходимо сделать проверку:
Как видим, подставив в уравнение решённые корни, у нас ответ получился тот же, что и в начале задачи, что говорит о правильном решении уравнений.
Ответ
Система уравнений имеет единственное решение: ,
,
.
Есть примеры, когда уравнение решений не имеет. Это может быть в том случае, когда определитель системы равен нулю, а определители при неизвестных неравны нулю. В таком случае говорят, что система несовместна, то есть не имеет решений. Посмотрим на следующем примере, как такое может быть.
Задача
Решить систему линейных уравнений методом Крамера:
Решение
Как и в предыдущих примерах находим главный определитель системы:
В этой системе определитель равняется нулю, соответственно, система несовместна и определенна или же несовместна и не имеет решений. Чтобы уточнить, надо найти определители при неизвестных так, как мы делали ранее:
Мы нашли определители при неизвестных и увидели, что все они не равны нулю. Поэтому система несовместна и не имеет решений.
Ответ
Система не имеет решений.
Часто в задачах на системы линейных уравнений встречаются такие уравнения, где есть не одинаковые буквы, то есть, кроме букв, которые обозначают переменные, есть ещё и другие буквы и они обозначают некоторое действительное число. На практике к таким уравнениям и системам уравнений приводят задачи на поиск общих свойств каких-либо явлений и предметов. То есть, изобрели вы какой-либо новый материал или устройство, а для описания его свойств, общих независимо от величины или количества экземпляра, нужно решить систему линейных уравнений, где вместо некоторых коэффициентов при переменных – буквы. Давайте и рассмотрим такой пример.
Задача
Решить систему линейных уравнений методом Крамера:
Решение
В этом примере – некоторое вещественное число. Находим главный определитель:
Находим определители при неизвестных:
Используя формулы Крамера, находим:
,
.
Ответ
,
.
И наконец, мы перешли к самой сложной системе уравнений с четырьмя неизвестными. Принцип решения такой же, как и в предыдущих примерах, но в связи с большой системой можно запутаться. Поэтому рассмотрим такое уравнение на примере.
Задача
Найти систему линейных уравнений методом Крамера:
Здесь действуют система определителей матрицы высших порядков, поэтому вычисления и формулы рассмотрены в этой теме, а мы сейчас просто посчитаем систему уравнений с четырьмя неизвестными.
Решение
В изначальном определители из элементов второй строки мы отнимали элементы четвёртой строки, а из элементов третьей строки отнимались элементы четвёртой строки, которые умножались на 2. Также отнимали из элементов четвёртой строки элементы первой строки, умноженной на два. Преобразования первоначальных определителей при трёх первых неизвестных произведены по такой же схеме. Теперь можно находить определители при неизвестных:
Для преобразований определителя при четвёртом неизвестном из элементов первой строки мы вычитали элементы четвёртой строки.
Теперь по формулам Крамера нужно найти:
,
,
,
.
Ответ
Итак, мы нашли корни системы линейного уравнения:
,
,
,
.
Видео:Математика без Ху!ни. Метод Гаусса.Скачать

Подведём итоги
При помощи метода Крамера можно решать системы линейных алгебраических уравнений в том случае, если определитель не равен нулю. Такой метод позволяет находить определители матриц такого порядка, как на
благодаря формулам Крамера, когда нужно найти неизвестные переменные. Если все свободные члены нулевые, тогда их определители равны нулю, так как в них содержится столбец с нулевыми элементами. И конечно же, если определители равняются нулю, лучше решать систему методом Гаусса, а не Крамера, только тогда ответ будет верный.
Рекомендуем почитать для общего развития
Решение методом Крамера в Excel
🎬 Видео
2 минуты на формулы Крамера ➜ Решение систем уравнений методом КрамераСкачать

Свойства систем линейных уравнений (01)Скачать

Исследовать систему уравнений на совместность и решить методом Гаусса и методом обратной матрицыСкачать

Системы линейных уравнений: Теорема Кронекера-КапеллиСкачать

Лекция 12. Системы линейных уравненийСкачать

Тимашев Д. А. - Алгебра, Часть 1. Лекции - 5. Система линейных уравненийСкачать

Математика Без Ху!ни. Система линейных уравнений. Метод Крамера.Скачать

§32 Исследование на совместность СЛАУСкачать


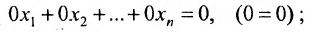
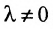 ;
;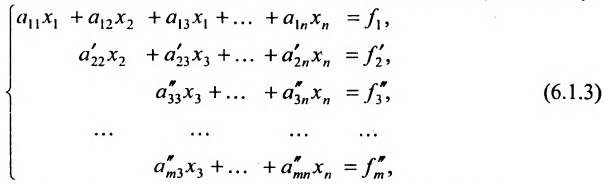
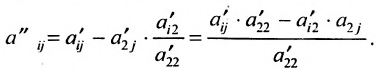
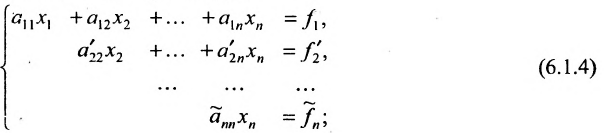
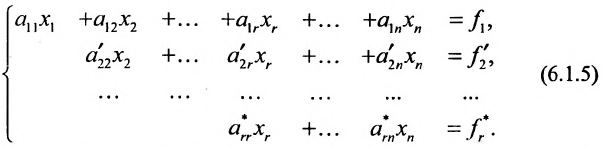

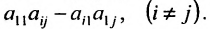
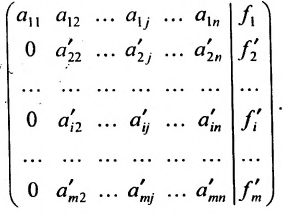
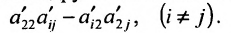

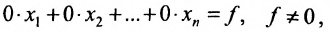
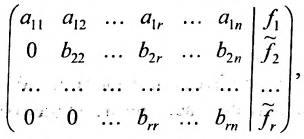
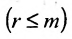
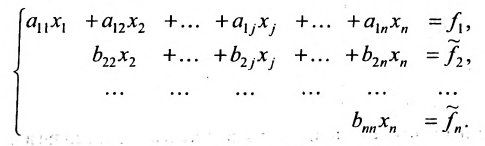
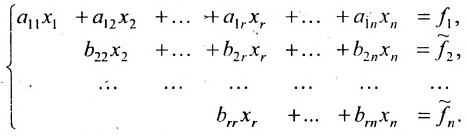
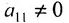 (если
(если 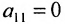 , строки матрицы можно переставить так, чтобы выполнялось условие
, строки матрицы можно переставить так, чтобы выполнялось условие 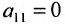 );
);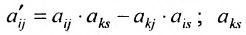 — разрешающий элемент (см. схему).
— разрешающий элемент (см. схему).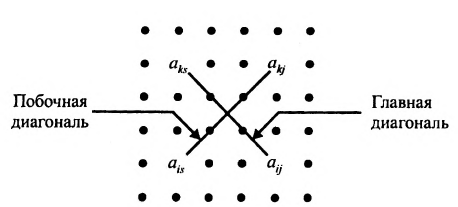
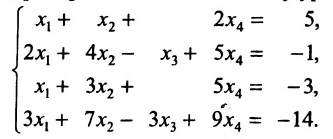


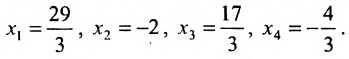
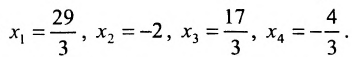
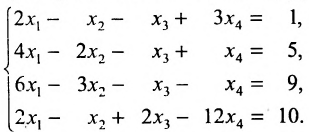

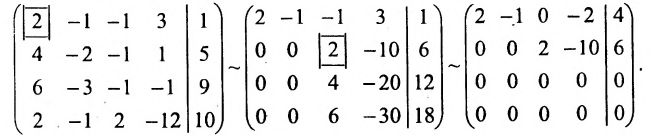

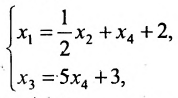
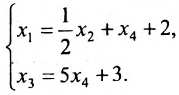
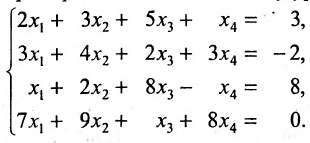
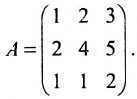
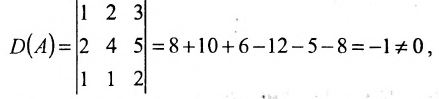

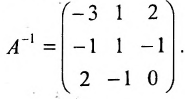
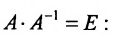
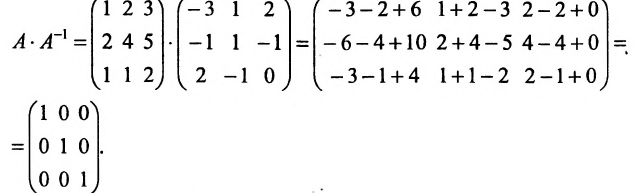
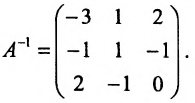
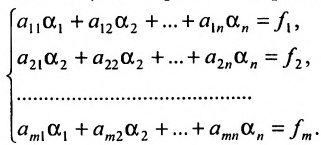
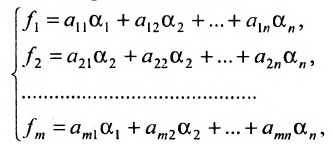
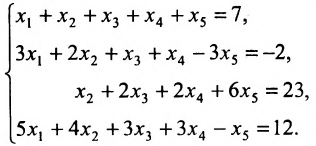

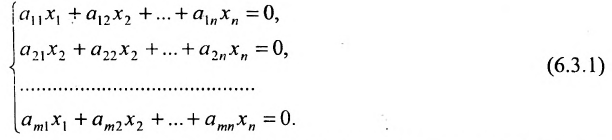
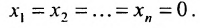
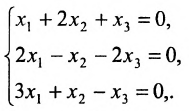
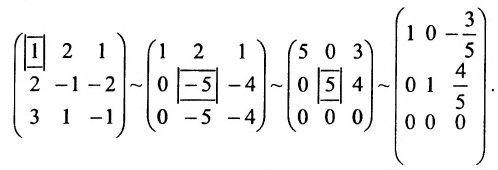
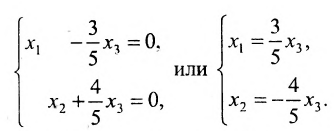
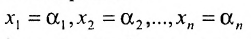
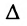 порядка n-r, отличный от нуля, в частности, определитель порядка n-r, у которого элементы главной диагонали равны единице, а остальные — нули.
порядка n-r, отличный от нуля, в частности, определитель порядка n-r, у которого элементы главной диагонали равны единице, а остальные — нули.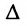 , и каждый раз из общего решения находим соответствующие значения базисных неизвестных.
, и каждый раз из общего решения находим соответствующие значения базисных неизвестных.