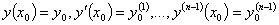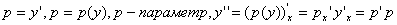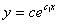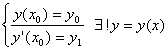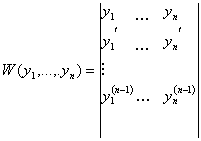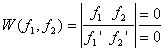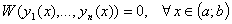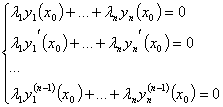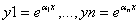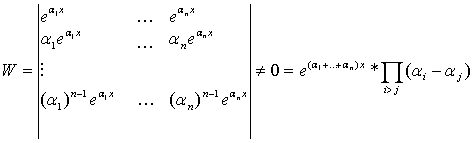Критерий линейной независимости решений однородного дифференциального уравнения n ного порядка

ЛИНЕЙНАЯ НЕЗАВИСМОСТЬ РЕШЕНИЙ ЛИНЕЙНОГО ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ

Высшая математика

Рассмотрим линейное однородное дифференциальное уравнение

Справедливо следующее этого уравнения.

Решения y ₁( x ), y ₂( x ), . y _n( x ) линейного однородного дифференциального уравнения линейно независимы на отрезке [ a ; b ] тогда и только тогда, когда определитель Вронского этих функций W ( x ; y ₁( x ), y ₂( x ), . y _n( x )) не обращается в нуль ни в одной точке отрезка [ a ; b ] .

Для определителя Вронского W ( x ; y ₁( x ), y ₂( x ), . y _n( x )) решений y ₁( x ), y ₂( x ), . y _n( x ) линейного однородного дифференциального уравнения с непрерывными на [ a ; b ] коэффициентами, справедлива формула Остроградского–Лиувилля:

Из формулы Остроградского-Лиувилля, в частности, следует:

Определитель Вронского. Критерий линейной независимости системы решений однородного ОДУ

1) Определителем Вронского W(x; y₁(x), y₂(x), . y_m(x)) называется определитель, первая строка которого образована функциями y₁(x),y₂(x), . y_m(x) из C_m-1[a, b] , а последующие строки образованы производными от функций предыдущей строки:

Доказательство: Так как функции линейно зависимы на , то существуют такие не все равные нулю числа , при которых выполняется тождество на . Дифференцируя его раз, получим систему уравнений

Эта однородная система по условию имеет нетривиальное решение (т. е. хотя бы одно ) при . Последнее возможно, когда определитель системы, который является определителем Вронского , тождественно равен нулю. Теорема доказана.

2) Функции y₁(x), y₂(x), . y_n(x) называются линейно независимыми на отрезке [a,b], если существуют постоянные б₁, б₂, . б_n равные нулю, такие, что для всех значений x из этого отрезка справедливо тождество

Для случая двух функций критерий линейной независимости можно записать в более простом виде: Функции y₁(x), y₂(x) будут линейно независимыми на отрезке [a,b], если их отношение на данном отрезке тождественно не равно постоянной:

Критерий линейной независимости решений однородного дифференциального уравнения n ного порядка

Дифференциальное уравнение n — ного порядка.

Дифференциальным уравнением n — ного порядка называется уравнение вида: 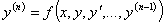для нахождения единственного решения неоюходимо знать начальные условия

Уравнения допускающие понижение порядка.

Можно отыскать решение этого уравнения, если уравнение имеет один из нижеследующих видов:

1) , решается двойным интегрированием.

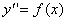
2) , делаем замену y ’= p = p ( x ), y ’’= p ’

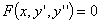
3) , тогда

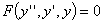
обозначим 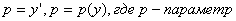, тогда pp ’ y = p 2

рассмотрим несколько случев

2) p ¹ 0 => p ¢ y=p или p ¢ /p=1/y => dp /p= dy /y

lnp = lny+c , p=cy, y ¢ =cy, dy /y= cdx =>

Линейные дифференциальные уравнения

Линейным дифференциальным уравнением называется уравнение вида:

(1)

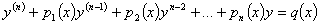
При q =0, уравнение называется однородным, q ¹ 0 неоднородным.

y ¢ + py = q –дифференциальное уравнение первого порядка.

y ¢ ¢ + p ₁ y ¢ + p ₂ y =0. если p ₁ и p ₂ непрерывны в рассматриваемой области, то $ ! 1-ая диф . кривая => единственное решение дифференциального уравнения.

Обозначим левую часть уравнения (1) при q ( x )=0 L ( y )=> L ( y )=0.

Отметим два свойства L ( y ).

Линейная зависимость функций

Функции y ₁ ,…, y_n называются линейно зависимыми, если $ λ₁ ,…, λ _n (| λ ₁ |+…+| λ_n | ¹ 0) такие что 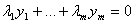соответственно функции называются линейно независимыми если не удовлетворяют уравнению (1).

Если функции y ₁ ( x ),…, y_n ( x )(все функции и их производные непрерывны и существуют до n -1 го порядка) линейно зависимы, то 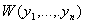=0.

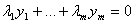
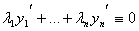
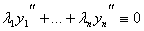
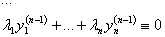
Так как функции линейно зависимы, то после дифференциирования получим:

, Эта система имеет ненулевое решение ó когда определитель этой системы равен 0. А этот определитель и есть определитель Вронского.

Если W ¹ 0 хотя бы в одной точке то функции линейно независимы.

Покажем, что если определитель равен нулю, то функции необязательно линейно зависимы. ,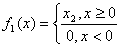

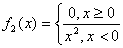
Рассмотрим произвольную точку x ₀ >0.

Утв . Если функции линейно независимы, то W =0

Если W =0, то неизвестно зависимы функции или нет.

Если W ¹ 0 в какой-либо точке, то функции линейно независимы.

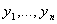
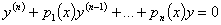
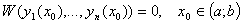
Теорема 2 П усть решения уравнения и тогда

Следствие: если 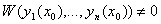хотя бы в одной точке ( a , b ) тогда » x ‘ ( a , b ) W ( x ) ¹ 0.

Так как W =0 в x ₀ , то 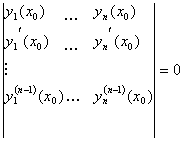так как определитель =0 то его строки и столбцы и строки линейно зависимы (их линейная комбинация равна 0). Значит

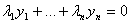
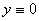
Рассмотрим функцию y = L ( y )=0, т.е. y — решение дифференциального уравнения. Следовательно , (*) ( первая строка в системе). Решение удовлетворяет (1) но начальным условиям удовлетворяет только одно решение (по теореме о существовании единственного решения). Получаем, что W =0 » x э ( a , b ).

y ( n ) =0 Решения: y ₁ =1, y ₂ = x , y ₃ = x 2 ,…, y_n = x n -1

этот определитель равен произведению чисел на главной диагонали (а все эти числа отличны от нуля), следовательно определитель отличен от нуля, следовательно функции линейно независимы.

Значит функции линейно независимы .

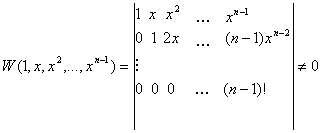
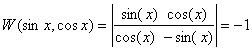
Фундаментальная система решений есть полная система решений дифференциального уравнения.

📹 Видео