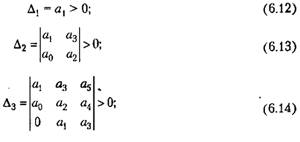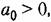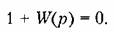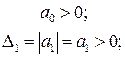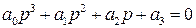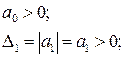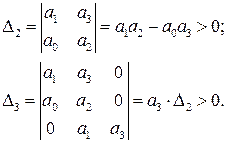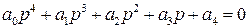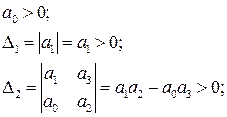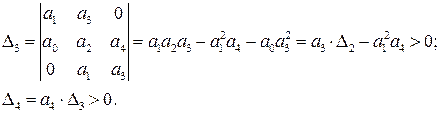Критерий гурвица для уравнения третьего порядка (6 видео)

Содержание

Критерий устойчивости Гурвица
IV. 2. 2. Критерий устойчивости Гурвица
Критерий Гурвица
🌟 Видео

Видео:Критерий ГурвицаСкачать

Критерий устойчивости Гурвица

Задача отыскания критерия устойчивости для систем, описываемых дифференциальными уравнениями любого порядка, была сформулирована Максвеллом в 1868 году. Эта задача была впервые решена в алгебраической форме Раусом в 1873 году для уравнений четвертой и пятой степени и в 1877 году — полностью.

Поскольку критерий Рауса дан в форме алгоритма, определяющего последовательность математических операций, необходимых для решения задачи, использование его в практике является неудобным. Поэтому большее распространение получил алгебраический критерий устойчивости, сформулированный в 1895 году математиком А. Гурвицем. Этот критерий был найден Гурвицем по просьбе словацкого профессора Стодолы, занимавшегося исследованием процесса регулирования турбин.

Ниже критерий Гурвица приводится без доказательства.

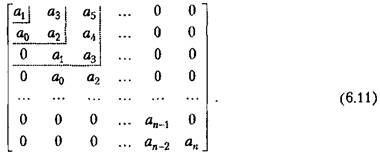
Для характеристического уравнения (6.9) составим квадратную матрицу (таблицу) коэффициентов, содержащую п строк и п столбцов:

Эта таблица составляется следующим образом.

. Каждая строка дополняется коэффициентами

с нарастающими индексами слева направо так, чтобы чередовались строки с нечетными и четными индексами. В случае отсутствия данного коэффициента, а также если индекс его меньше нуля или больше п, на месте его пишется нуль.

должны быть больше

нуля все п определителей Гурвица, получаемых из квадратной матрицы коэффициентов.

Определители Гурвица составяются по следующему правилу (см. (6.11)):

Последний определитель включает в себя всю матрицу. Но так как в последнем столбце матрицы все элементы, кроме нижнего, равны нулю, то последний определитель Гурвица выражается через предпоследний следующим образом:

т. е. к положительности свободного члена характеристического уравнения.

Первое условие соответствует границе устойчивости первого типа (апериодическая граница устойчивости) и второе — границе устойчивости второго типа (колебательная граница устойчивости).

Раскрывая определители, фигурирующие в общей формулировке критерия устойчивости Гурвица, можно получить в виде частных случаев критерии устойчивости для системы первого, второго, третьего, четвертого и более высоких порядков.

порядка

Для этого уравнения критерий Гурвица дает

т. е. коэффициенты характеристического уравнения должны быть положительными.

порядка

Для этого уравнения критерий Гурвица требует

Таким образом, и для уравнения второго порядка необходимым и достаточным условием устойчивости является положительность всех коэффициентов характеристического уравнения.

3. У р а в н е н и е третьего поря д к а

Для этого уравнения получаем условия

4. Уравнение четвертого порядка

На основании критерия Гурвица можно получить, что для уравнения четвертого порядка, кроме положительности всех коэффициентов, требуется выполнение условия

пятого поря д к а

Для уравнения пятого порядка, кроме положительности всех коэффициентов, должны выполняться еще два условия:

Как видно, уже для уравнения пятой степени условия устойчивости но критерию Гурвица получаются достаточно громоздкими. Поэтому использование этого критерия практически ограничивается уравнениями четвертого порядка.

Существенным недостатком критерия Гурвица является также то, что для уравнений высоких порядков в лучшем случае можно получить ответ о том, устойчива или неустойчива система автоматического управления. При этом в случае неустойчивости системы критерий не дает ответа на то, каким образом надо изменить параметры системы, чтобы сделать ее устойчивой. Это обстоятельство привело к поискам других критериев, которые были бы более удобными в инженерной практике.

Для иллюстрации применения критерия Гурвица рассмотрим пример на определение устойчивости дистанционной следящей системы. Принципиальная и структурная схемы изображены на рис. 6.4. В качестве чувствительного элемента использованы два сельсина (СД и СП), включенные по трансформаторной схеме. Передаточная функция сельсинов равна коэффициенту передачи схемы:

— электромеханическая постоянная времени двигателя совместно с оконечным каскадом усилителя. Передаточная функция редуктора (Р) равна его коэффициенту передачи, определяемому передаточным отношением:

Так как цепь управления состоит из включенных последовательно звеньев, то передаточная функция разомкнутой цепи будет равна произведению передаточных функций отдельных звеньев:

— общий коэффициент усиления разомкнутой цепи.

получаем

В данном случае характеристическое уравнение имеет третий порядок. Нетрудно видеть, что условие положительности всех коэффициентов выполняется всегда, если выполнено условие К> О, что будет при правильном согласовании направления вращения двигателя со знаком рассогласования.

накладываемое на коэффициенты характеристического уравнения, сводится при подстановке значений коэффициентов

, к неравенству

которое и является условием устойчивости рассматриваемой системы.

Из этого неравенства, в частности, можно заметить, что увеличение каждой постоянной времени сказывается отрицательно на устойчивости системы, так как при

этом снижается предельное значение общего коэффициента усиления к, при котором система еще остается устойчивой.

измеряется датчиком угла (нотенциометрическим, индукционным или др.), установленным на гиростабилизированной платформе. Передаточная функция датчика

Для формирования алгоритма управления дополнительно устанавливается датчик угловой скорости (ДУС). Напряжение на его выходе пропорционально производной от отклонения. Передаточная функция ДУС в идеальном случае

суммируются:

и производной от отклонения (см. § 2.2). Передаточная функция усилительно-преобразовательного устройства

Его передаточная функция

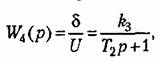
где 8 — угол отклонения управляющих органов ракеты.

» Передаточная функция управляемого объекта (ракеты) по управляющему воздействию в простейшем случае может быть, например, такой:

Передаточная функция объекта по возмущению

Корни характеристического уравнения объекта

свидетельствует о том, что сам объект

неустойчив, или, как говорят, статически неустойчив. Он ведет себя подобно шару на рис. 6.1, б. Иными словами, при малейшем отклонении, вызванном, например, возмущающим воздействием, стартующая вертикально ракета без системы автоматического управления опрокидывается.

Передаточная «функция разомкнутой системы равна произведению передаточных функций, входящих в контур отточки размыкания до точки размыкания (см. рис. 6.5):

в указанный контур не входит.

т. е. разомкнутая система неустойчива.

Характеристическое уравнение замкнутой системы можно получить, приравняв нулю сумму полиномов числителя и знаменателя передаточной функции разомкнутой системы:

Таким образом, необходимыми и достаточными условиями устойчивости замкнутой системы будут:

Первое из них при выполнении двух других всегда выполняется. Следует обратить внимание па то, что если бы управление осуществлялось только по отклонению

т. е. являлась бы структурно неустойчивой.

— на колебательной границе,

Видео:29) КРИТЕРИИ УСТОЙЧИВОСТИ. КРИТЕРИЙ ГУРВИЦАСкачать

IV. 2. 2. Критерий устойчивости Гурвица

Наиболее распространенная в технической практике форма алгебраического критерия устойчивости известна под названием критерия Гурвица (1895). Этот критерий может быть применен для определения устойчивости как разомкнутых, так и замкнутых САР в зависимости от того, характеристическое уравнение какой из вышеназванных САР принято для исследования.

Ниже рассматриваемый критерий приводится без доказательства.

Для характеристического уравнения (IV. 1. 3) составим квадратную матрицу (таблицу) коэффициентов, содержащую n строк и n столбцов (матрицу Гурвица)

(IV. 2. 1)

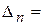
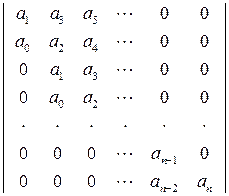
Эта таблица составляется следующим образом.

По диагонали от левого верхнего до правого нижнего углов выписываются все коэффициенты по порядку от a₁ до a _n._.Каждая строка дополняется коэффициентами с возрастающими слева направо индексами так, чтобы чередовались строки с нечётными и чётными индексами. В случае отсутствия данного коэффициента, а так же если индекс его меньше нуля или больше n, на месте его пишется нуль. Можно заметить, что индексы в столбцах нарастают снизу вверх, поэтому нетрудно понять, что в правом крайнем столбце единственным элементом, отличном от 0, будет нижний элемент a_n .

Главные диагональные миноры или определители матрицы Гурвица

(IV. 2. 1) имеют вид

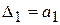
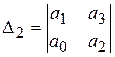
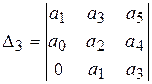
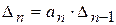
Формулировка критерия устойчивости Гурвица обычно дается в следующем виде:

Для устойчивости САР необходимо и достаточно, чтобы при a₀>0 все главные диагональные миноры матрицы Гурвица были бы больше нуля 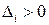(i=1, 2, …n).

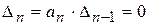
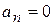
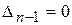
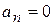
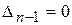
Условие нахождения системы на границе устойчивости можно получить, приравняв нулю последний минор при положительности всех остальных главных диагональных миноров. Это условие распадается на два условия: и . Первое условие свидетельствует о том, что характеристическое уравнение имеет один нулевой корень, это соответствует границе устойчивости апериодического типа, а второе говорит о наличии пары чисто мнимых корней и существовании колебательной границы устойчивости.

Если нас интересует граничное значение какого-то параметра (например, коэффициента усиления k_гр), при котором САР становится нейтральной, то его можно найти из выражения

. ( IV. 2. 2)

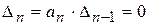
Для часто встречающихся на практике конкретных случаев условия устойчивости Гурвица имеют следующий вид.

Уравнение первого порядка.

Характеристическое уравнение САР в этом случае представляется следующим образом

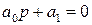
Здесь матрица Гурвица совпадает с ее первым диагональным минором .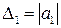

Следовательно, необходимым и достаточным условием устойчивости по Гурвицу является положительность коэффициентов a₀ и a₁.

Уравнение второго порядка.

Характеристическое уравнение здесь таково

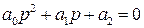
поэтому матрица Гурвица имеет вид

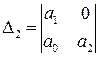
Запишем необходимые и достаточные условия устойчивости Гурвица

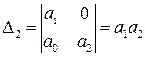
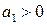
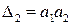
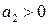
Поскольку , то будет положительным только при и, значит, САР будет устойчива при положительности всех коэффициентов а₀, a₁ и a₂.

Как уже говорилось выше, для САР первого и второго порядков необходимые условия устойчивости Стодолы (т.е. положительность коэффициентов характеристических уравнений) является, как следует из критерия Гурвица, и достаточными.

Уравнение третьего порядка.

Для характеристического уравнения третьего порядка

матрица Гурвица имеет вид

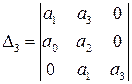
Необходимые и достаточные условия устойчивости Гурвица таковы:

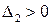
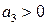
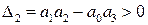
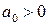
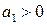
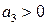
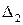
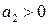
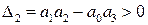
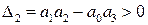
Поскольку по Гурвицу для устойчивости системы все миноры должны быть положительными, из последнего неравенства (если ) обязательно следует . Обратимся теперь ко второму главному диагональному минору . Так как мы установили, что , и , то в этом выражении второе слагаемое всегда положительное, а сам минор может быть положительным только при . Итак, для устойчивости САР третьего порядка мы получили необходимые условия, выражающиеся в положительности всех коэффициентов характеристического уравнения. Однако, этих условий недостаточно, т. к. из второго минора видно, что при положительности всех коэффициентов рассматриваемый минор будет положительным только тогда, когда первое слагаемое больше второго. Таким образом, в САР третьего порядка для устойчивости к необходимым условиям добавляется еще условие достаточности

. (IV. 2.3)

Уравнение четвертого порядка.

Для САР четвертого порядка уравнение (IV. 1.3) имеет вид

и тогда матрица Гурвица выглядит следующим образом

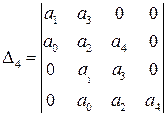
Выпишем, как обычно, условия устойчивости по Гурвицу

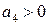
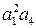
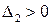
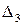
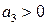
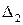
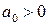
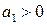
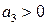
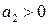
При всех положительных минорах последнее неравенство выполняется лишь при и тогда в предпоследнем неравенстве второе слагаемое положительно. При минор будет положительным только при . Отсюда следует, что будет положительным при , и , только при .

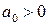
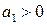
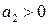
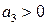
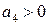
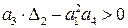
Итак, необходимые условия устойчивости , , , и мы установили. Сюда необходимо добавить достаточное условие

которое включает в себя требование

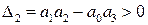
Применение критерия Гурвица для исследования устойчивости САР пятого и больших порядков нецелесообразно, т. к. приводит к громоздким вычисления по разрешению миноров, т.е. раскрытию определителей больших порядков. В таких случаях рекомендуется использовать частотные критерии.

Видео:Теория автоматического управления. Лекция 9. Критерий ГурвицаСкачать

Критерий Гурвица

Назначение сервиса . С помощью онлайн калькулятора выбирается оптимальная стратегия по критерию Гурвица. Результаты вычислений оформляются в отчете формата Word (см. Пример оформления).

Пример . Исходные данные:

8	4	6	20
7	7	7	7
6	12	8	10

Критерий Вальда.
По критерию Вальда за оптимальную принимается чистая стратегия, которая в наихудших условиях гарантирует максимальный выигрыш, т.е.
a = max(min a_ij)
Критерий Вальда ориентирует статистику на самые неблагоприятные состояния природы, т.е. этот критерий выражает пессимистическую оценку ситуации.

A_i	П₁	П₂	П₃	П₄	min(a_ij)
A₁	8	4	6	20	4
A₂	7	7	7	7	7
A₃	6	12	8	10	6

Выбираем из (4; 7; 6) максимальный элемент max=7
Вывод: выбираем стратегию N=2.
Критерий Севиджа.
Критерий минимального риска Севиджа рекомендует выбирать в качестве оптимальной стратегии ту, при которой величина максимального риска минимизируется в наихудших условиях, т.е. обеспечивается:
a = min(max r_ij)
Критерий Сэвиджа ориентирует статистику на самые неблагоприятные состояния природы, т.е. этот критерий выражает пессимистическую оценку ситуации.
Находим матрицу рисков.
Риск – мера несоответствия между разными возможными результатами принятия определенных стратегий. Максимальный выигрыш в j-м столбце b_j = max(a_ij) характеризует благоприятность состояния природы.
1. Рассчитываем 1-й столбец матрицы рисков.
r₁₁ = 8 — 8 = 0; r₂₁ = 8 — 7 = 1; r₃₁ = 8 — 6 = 2;
2. Рассчитываем 2-й столбец матрицы рисков.
r₁₂ = 12 — 4 = 8; r₂₂ = 12 — 7 = 5; r₃₂ = 12 — 12 = 0;
3. Рассчитываем 3-й столбец матрицы рисков.
r₁₃ = 8 — 6 = 2; r₂₃ = 8 — 7 = 1; r₃₃ = 8 — 8 = 0;
4. Рассчитываем 4-й столбец матрицы рисков.
r₁₄ = 20 — 20 = 0; r₂₄ = 20 — 7 = 13; r₃₄ = 20 — 10 = 10

A_i	П₁	П₂	П₃	П₄
A₁	0	8	2	0
A₂	1	5	1	13
A₃	2	0	0	10

Результаты вычислений оформим в виде таблицы.

A_i	П₁	П₂	П₃	П₄	max(a_ij)
A₁	0	8	2	0	8
A₂	1	5	1	13	13
A₃	2	0	0	10	10

Выбираем из (8; 13; 10) минимальный элемент min=8
Вывод: выбираем стратегию N=1.
Критерий Гурвица.
Критерий Гурвица является критерием пессимизма — оптимизма. За оптимальную принимается та стратегия, для которой выполняется соотношение:
max(s_i)
где s_i = y min(a_ij) + (1-y)max(a_ij)
При y = 1 получим критерий Вальде, при y = 0 получим – оптимистический критерий (максимакс).
Критерий Гурвица учитывает возможность как наихудшего, так и наилучшего для человека поведения природы. Как выбирается y? Чем хуже последствия ошибочных решений, тем больше желание застраховаться от ошибок, тем y ближе к 1.
Рассчитываем s_i.
s₁ = 0.5•4+(1-0.5)•20 = 12
s₂ = 0.5•7+(1-0.5)•7 = 7
s₃ = 0.5•6+(1-0.5)•12 = 9

A_i	П₁	П₂	П₃	П₄	min(a_ij)	max(a_ij)	y min(a_ij) + (1-y)max(a_ij)
A₁	8	4	6	20	4	20	12
A₂	7	7	7	7	7	7	7
A₃	6	12	8	10	6	12	9

Выбираем из (12; 7; 9) максимальный элемент max=12
Вывод: выбираем стратегию N=1.
Обобщенный критерий Гурвица.
Данный критерий является некоторым обобщением критериев крайнего пессимизма и крайнего оптимизма и также представляет собой частный случай обобщенного критерия Гурвица относительно выигрышей при следующем допущении:
λ₁=1-λ, λ2=λ3=…=λ_n-1=0, λ_n=λ, где 0 ≤ λ ≤ 1
Тогда показатель эффективности стратегии A_i по Гурвицу есть:
G_i=(1-λ)min a_ij + λmax a_ij
Оптимальной стратегией A_i0 считается стратегия с максимальным значением показателя эффективности.
Строим вспомогательную матрицу B, полученную путем упорядочивания показателей доходностей в каждой строке.
Подход пессимиста. λ выбирается из условия невозрастания среднего:

G₁ = 0.304 • 4+(1-0.304) • 20 = 15.143; G₂ = 0.304 • 7+(1-0.304) • 7 = 7; G₃ = 0.304 • 6+(1-0.304) • 12 = 10.179;
Подход оптимиста. λ выбирается из условия неубывания среднего:

G₁ = 0.696 • 4+(1-0.696) • 20 = 8.857; G₂ = 0.696 • 7+(1-0.696) • 7 = 7; G₃ = 0.696 • 6+(1-0.696) • 12 = 7.821

A_i	П₁	П₂	П₃	П₄	min(a_ij)	max(a_ij)	Подход пессимиста	Подход оптимиста
A₁	4	6	8	20	4	20	15.14	8.86
A₂	7	7	7	7	7	7	7	7
A₃	6	8	10	12	6	12	10.18	7.82

Выбираем из (15.143; 7; 10.179) максимальный элемент max=15.14
Вывод: выбираем стратегию N=1.
Оптимальные стратегии по обобщенному критерию Гурвица.
b = 17 + 21 + 25 + 39 = 102
Показатели эффективности по Гурвицу.
Подход пессимиста

Подход оптимиста