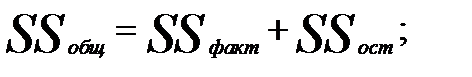Как и в случае парной регрессии для оценки качества полученного множественной уравнения регрессии (3.6) можно использовать коэффициентмножественной детерминации, представляющий собой отношение факторной суммы квадратов остатков к их общей сумме квадратов:

(3.35)

— остаточная сумма квадратов.

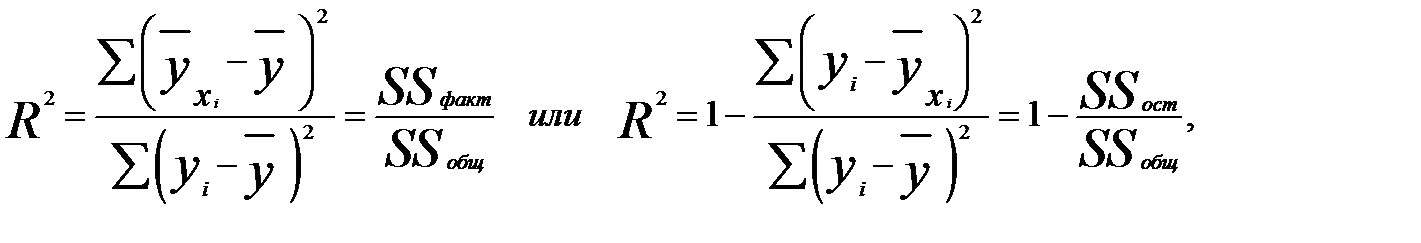
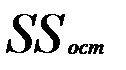
Коэффициент множественной корреляции равен корню из коэффициента множественной детерминации:

(3.36)

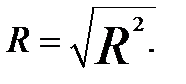
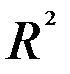
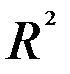
Оба показателя изменяются от нуля до единицы. показывает, какая часть вариации результативного признака y объяснена уравнением регрессии. Чем выше значение , тем лучше данная модель согласуется с данными наблюдений.

Коэффициент множественной корреляции R используется для оценки тесноты связи факторов с исследуемым признаком. Чем ближе величина R к единице, тем теснее данная связь, тем лучше теоретическая зависимость согласуется с эмпирическими данными.

Видео:Критерий Фишера для проверки адекватности построенной регрессииСкачать

Введём понятие дисперсии на одну степень свободы (df).

, (3.37)

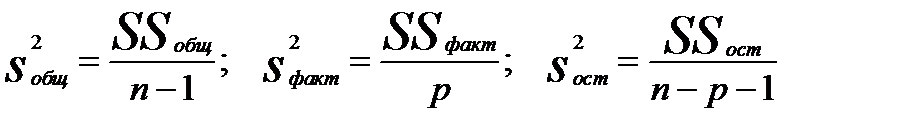
где (n-1) — количество степеней свободы для общей дисперсии;

p–для факторнойдисперсии (количество независимых переменных в уравнении регрессии);

(n-p-1) – для остаточной дисперсии.

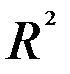
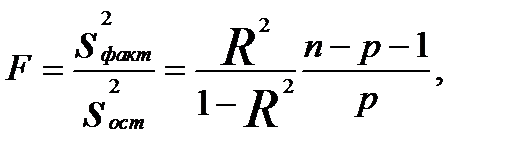
Оценка статистической значимости уравнения регрессии (а также коэффициента детерминации ) осуществляется с помощью F-критерия Фишера

(3.38)

Согласно F-критерию Фишера, выдвигаемая «нулевая» гипотеза H0 о статистической незначимости уравнения регрессии отвергается при выполнении условия F >Fкрит, где Fкрит определяется по таблицам F-критерия Фишера по двум степеням свободы k1 = p, k2 = n-p-1 и заданному уровню значимости α.

Величина коэффициента множественной корреляции R не может быть меньше максимального парного индекса корреляции max .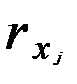

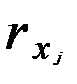
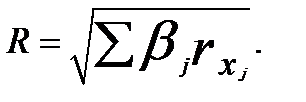
В случае линейной зависимости (3.6) коэффициент корреляции R связан с парными коэффициентами корреляции соотношением

(3.39)

Использование коэффициента множественной детерминации R2 для оценки качества модели, обладает тем недостатком, что включение в модель нового фактора (даже несущественного) автоматически увеличивает величину .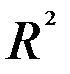

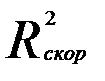
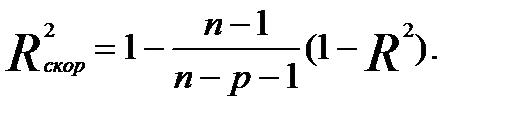
Поэтому при большом количестве факторов предпочтительнее использовать, так называемый, скорректированный, улучшенный (adjusted) коэффициент множественной детерминации , определяемый соотношением

(3.40)

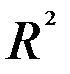
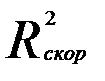
Чем больше величина p, тем сильнее различия и .

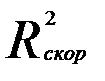
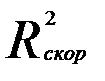
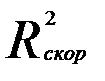
При использовании для оценки целесообразности включения фактора в уравнение регрессии следует учитывать, что увеличение при включении нового фактора не обязательно свидетельствует о его значимости, так как значение увеличивается всегда, когда t — статистика по модулю больше единицы.

При заданном объеме наблюдений и при прочих равных условиях с увеличением числа независимых переменных (параметров) скорректированный коэффициент множественной детерминации убывает. При небольшом числе наблюдений скорректированная величина коэффициента множественной детерминации 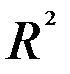имеет тенденцию переоценивать долю вариации результативного признака, связанную с влиянием факторов, включенных в регрессионную модель.

Отметим, что низкое значение коэффициента множественной корреляции и коэффициента множественной детерминации 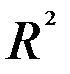может быть обусловлено следующими причинами:

Видео:Эконометрика. Оценка значимости уравнения регрессии. Критерий ФишераСкачать

– в регрессионную модель не включены существенные факторы;

– неверно выбрана форма аналитической зависимости, не отражающая реальные соотношения между переменными, включенными в модель.

Использование критерия Фишера для проверки значимости регрессионной модели

Критерий Фишера для регрессионной модели отражает, насколько хорошо эта модель объясняет общую дисперсию зависимой переменной. Расчет критерия выполняется по уравнению:

где R — коэффициент корреляции;
f₁ и f₂ — число степеней свободы.

Видео:Проверка адекватности регрессии. Критерий ФишераСкачать

Первая дробь в уравнении равна отношению объясненной дисперсии к необъясненной. Каждая из этих дисперсий делится на свою степень свободы (вторая дробь в выражении). Число степеней свободы объясненной дисперсии f₁ равно количеству объясняющих переменных (например, для линейной модели вида Y=A*X+B получаем f₁=1). Число степеней свободы необъясненной дисперсии f₂ = N—k-1, где N-количество экспериментальных точек, k-количество объясняющих переменных (например, для модели Y=A*X+B подставляем k=1).

Для проверки значимости уравнения регрессии вычисленное значение критерия Фишера сравнивают с табличным, взятым для числа степеней свободы f₁ (бóльшая дисперсия) и f₂ (меньшая дисперсия) на выбранном уровне значимости (обычно 0.05). Если рассчитанный критерий Фишера выше, чем табличный, то объясненная дисперсия существенно больше, чем необъясненная, и модель является значимой.

Коэффициент корреляции и F-критерий, наряду с параметрами регрессионной модели, как правило, вычисляются в алгоритмах, реализующих метод наименьших квадратов.

Проверка качества уравнения регрессии. F-критерий Фишера

Оценка качества полученного уравнения регрессии основывается на мето-дах дисперсионного анализа.

Видео:Регрессия в ExcelСкачать

Наблюдаемые значения результативного признака y_i можно представить в виде суммы двух составляющих ŷ_i и е_i

Величина ŷ_i=а+ b·х_i представляет собой расчетное значение переменной у в наблюдении i. Остаток е_i есть расхождение между наблюдаемым и расчетны-ми значениями переменной у, или необъясненная с помощью уравнения рег-рессии часть переменной у.

Из (2.21) следует следующее соотношение между дисперсиями наблюдае-мых значений переменной D(y), ее расчетных значений D(ŷ) и остатков D(е)

называют коэффициентом детерминации и используют для характеристики качества уравнения регрессии или соответствующей модели связи.

Соотношение (2.23) можно представить в альтернативном виде

Коэффициент детерминации R 2 принимает значения в диапазоне от нуля до

Коэффициент детерминации R 2 показывает, какая часть дисперсии резуль-тативного признака y объяснена уравнением регрессии. Например, значение R 2 = 0,56говорит о том,что соответствующее уравнение регрессии объясняет56 % дисперсии результативного признака.

Чем больше R 2 , тем большая часть дисперсии результативного признака y объясняется уравнением регрессии и тем лучше уравнение регрессии описывает исходные данные. При отсутствии зависимости между у и x коэффициент детер-минации R 2 будет близок к нулю. Таким образом, коэффициент детерминации R 2 может применяться для оценки качества (точности) уравнения регрессии.

Видео:Критерий Стьюдента и Фишера в Excel, проверка уравнения множественной регрессии в ExcelСкачать

Возникает вопрос, при каких значениях R 2 уравнение регрессии следует считать статистически незначимым, что делает необоснованным его использо-вание в анализе. Ответ на этот вопрос дает F-критерий Фишера.

Введем следующие обозначения:

n k 1

где k число независимых переменных в уравнении регрессии (для парной рег-рессии k= 1), в случае нормально распределенной ошибки ε_i является F-статис-тикой Фишера (случайная величина, распределенная по закону Фишера) с чис-лом степеней свободы k₁=k,k₂=n k1.

Согласно F-критерию Фишера, выдвигается « нулевая» гипотеза H₀ о ста-тистической незначимости уравнения регрессии (т. е. о статистически незначи-мом отличии величины F от нуля). Эта гипотеза отвергается при выполнении условия F>F_крит, где F_крит определяется по таблицам F-критерия Фишера (П3,

П4) при числе степеней свободы k₁=k, k₂=n k1 и заданному уровню зна-чимости α.

Видео:A.4.14 Точный тест Фишера (введение в статистику)Скачать

Уровнем значимости (обозначаетсяα)в статистических гипотезах называ-ется вероятность отвергнуть верную гипотезу (это, так называемая, ошибка первого рода). Уровень значимости α обычно принимает значения 0,05 и 0,01, что соответствует вероятности совершения ошибки первого рода 5 % и 1 %.

Используя соотношение (2.24), величину F можно выразить через коэффи-циент детерминации R 2

Например, по данным 30 наблюдений было получено уравнение регрессии y = 50,5 + 3,2x и R 2 = 0,60.

Необходимо проверить его значимость при уровне значимости α = 0,05. Определим величину F-статистики, учитывая, что k= 1

По таблицам F-критерия Фишера при

находим F_крит= 4,20. Так как F= 42 >F_крит= 4,20 , то делаем вывод о статисти-ческой значимости уравнения регрессии.

📹 Видео

Эконометрика. Оценка значимости параметров уравнения регрессии. Критерий Стьюдента.Скачать

Простые показатели качества модели регрессии (R2, критерии Акаике и Шварца)Скачать

Однофакторная регрессионная модель. Коэффициенты детерминации, корреляции. Критерий ФишераСкачать

Проверка гипотезы о значимости коэффициентов уравнения регрессииСкачать

Пример проверки гипотезы о незначимости регрессииСкачать

12-05 Информация Фишера и свойства ММП оценокСкачать

Статистический метод (критерий): как выбрать для анализа?Скачать

Тема 6. Эконометрические тесты и показатели качества регрессии.Скачать

Эконометрика. Точечный и интервальный прогнозы.Скачать

Расчет точного теста Фишера в excelСкачать

Линейная регрессия. Оценка качества моделиСкачать

10 Тест ФишераСкачать

Эконометрика. Линейная парная регрессияСкачать

Проверка гипотезы о нескольких линейных ограниченияхСкачать