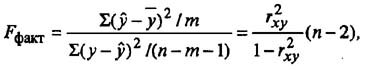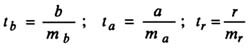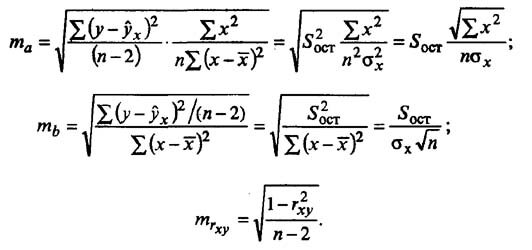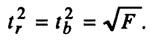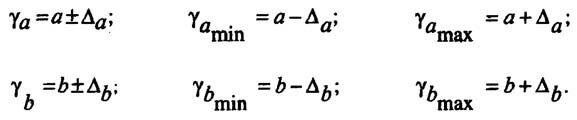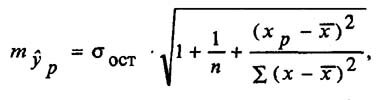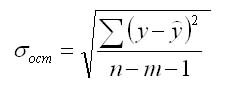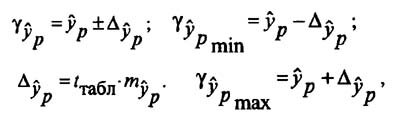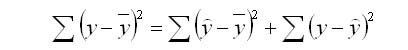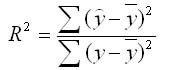Быстрая навигация по странице:

Видео:Критерий Стьюдента и Фишера в Excel, проверка уравнения множественной регрессии в ExcelСкачать

Понятие F-критерия Фишера

F-критерий Фишера – это один из важных статистических критериев, используемых при проверке значимости как уравнения регрессии в целом, так и отдельных его коэффициентов. Для оценки статистической значимости отдельных коэффициентов уравнения множественной регрессии используют так называемые частные F-критерий Фишера. Критическое значение данного критерия при проведении анализа определяется по специальным таблицам, а также может быть определено при помощи специальных функций в различных компьютерных программах. Например, в MS Excel для этого может быть использована функция FРАСПОБР.

Размещено на www.rnz.ru

Видео:Критерий Фишера для проверки адекватности построенной регрессииСкачать

Формулы расчета F-критерия Фишера

В общем виде F-критерий Фишера рассчитывается по следующей формуле:

F = S 2 _факт / S 2 _ост;
где: S 2 _факт — факторная дисперсия;
S 2 _ост — остаточная дисперсия

Соответствующие виды дисперсий определяются по следующим формулам:

формула расчета факторной дисперсии

формула расчета остаточной дисперсии

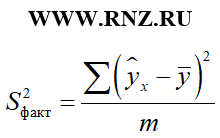
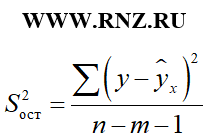
В приведенных формулах n – это число наблюдений, m – число параметров при переменной x (то есть количество факторов в модели регрессии).

При этом необходимо обратить внимание на то, что в зависимости от типа исследуемой модели регрессии применяемая формула определения F-критерия Фишера может изменяться. Например, для расчета F-критерия Фишера для парной линейной регрессии может использоваться следующая формула:

формула расчета F-критерия Фишера для парной линейной регрессии

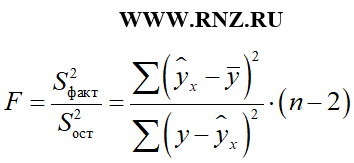
При использовании коэффициента детерминации расчет F-критерия Фишера для парной линейной регрессии может быть выполнен по такой формуле:

формула расчета F-критерия Фишера через коэффициент детерминации

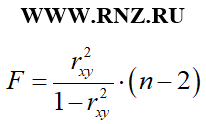
Для парной нелинейной модели регрессии расчет F-критерия Фишера может быть осуществлен через связь с индексом детерминации по следующей формуле:

формула расчета F-критерия Фишера для парной нелинейной модели регрессии через индекс детерминации

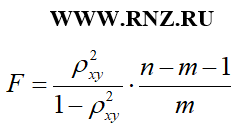
Описания параметров n и m приведено выше.

Для уравнения множественной регрессии F-критерий Фишера рассчитывается по следующей формуле:

формула расчета F-критерия Фишера для уравнения множественной регрессии

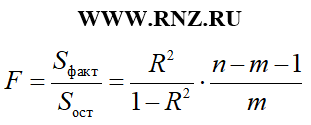
В процессе исследования уравнения множественной регрессии кроме общего F-критерий Фишера могут быть рассчитаны частные F-критерии. В случае анализа уравнения с двумя регрессорами (переменными) вычисление частных F-критериев может быть выполнено по следующим формулам:

формула расчета частных F-критериев Фишера для уравнения множественной регрессии

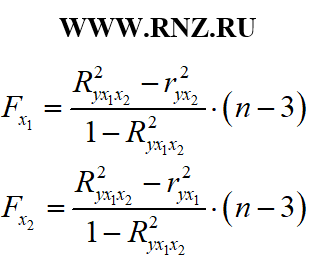
Видео:Эконометрика. Оценка значимости уравнения регрессии. Критерий ФишераСкачать

Значимость F-критерия Фишера

Для определения статистической значимости рассчитанного значения F-критерия Фишера его сравнивают с критическим или табличным значением. При этом табличное значение определяется на основе числа наблюдений, степеней свободы и заданного уровня значимости следующим образом: Fтабл (a; k₁; k₂), где k₁ = m – это количество факторов в построенной регрессионной модели, а k₂ = n – m – 1 (n – число наблюдений). Для частного F-критерия k₁ = 1, k₂ = n – m – 1 (n – число наблюдений).

Интерпретация F — критерия Фишера для уравнения регрессии в целом следующая: в том случае, когда фактическая величина F — критерия Фишера больше табличного показателя, то уравнение регрессии в целом является статистически значимым.

Интерпретация частного F — критерия Фишера следующая: в том случае, когда рассчитанная величина частного F_xi превышает критическое значение, то дополнительное включение фактора x_i в регрессионную модель статистически оправданно и коэффициент регрессии b_i при соответствующем факторе x_i статистически значим. Но если рассчитанная величина F_xi меньше табличного, то дополнительное включение в модель фактора x_i не оправдано, т.к. данный фактор, как и коэффициент регрессии при нём является статистически незначимым.

Видео:Проверка адекватности регрессии. Критерий ФишераСкачать

Пример расчета F-критерия Фишера

Приведем условные примеры расчета F-критерия Фишера

Пример №1. Предположим, что исследуется регрессия с одним фактором (парная), на основе 30-ти наблюдений, в которой коэффициент детерминации составил 0,77. Тогда по приведённой выше формуле фактическое значение F-критерия Фишера составит: F = 0,77/(1-0,77)*(30-2) = 93,74. Для определения значимости его нужно сравнить с табличным значением. Предположим, что используется уровень значимости α = 0.05. Тогда критическая величины F_табл(0,05; 1; 30-1-1) = 4,2. Так как F > F_табл, то полученное уравнение регрессии является статистически значимым.

Пример №2. Предположим, что исследуется множественная регрессия с тремя факторами, на основе 40 наблюдений, в которой коэффициент множественной детерминации составил 0,89. Тогда по приведённой выше формуле фактическое значение F-критерия Фишера для уравнения множественной регрессии составит: F = (0,89/(1-0,89))*((40-3-1)/3) = 97,09. Для определения значимости его нужно сравнить с табличным значением. Предположим, что используется уровень значимости α = 0.05. Тогда критическая величины F_табл(0,05; 3; 40-3-1) = 2,87. Так как F > F_табл, то полученное уравнение множественной регрессии является статистически значимым.

Видео:10 Тест ФишераСкачать

Онлайн-калькулятор F-критерия Фишера

Представляем онлайн калькулятор расчета F-критерия Фишера, используя который, Вы можете самостоятельно определить значения соответствующего показателя. При заполнении приведенной формы калькулятора внимательно соблюдайте размерность полей, что позволит выполнить и точно выполнить вычисления. В приведенной форме онлайн калькулятора уже содержатся данные условного примера, чтобы пользователь мог посмотреть, как это работает и посмотреть, как правильно заполнять поля. Для определения значений соответствующих показателей по своим данным просто внесите их в соответствующие поля формы онлайн калькулятора и нажмите кнопку «Выполнить вычисления». При заполнении формы соблюдайте размерность показателей! Дробные числа записываются с точной, а не запятой!

Калькулятор позволяет вычислить значение F-критерия Фишера на основе коэффициента детерминации (первый вариант) или на основе показателей сумм квадратов отклонений, т.е. используя элементы дисперсионного анализа. Выберите необходимый способ и выполните соответствующие вычисления. Для проверки статистической значимости используется уровень значимости α = 0.05.

Онлайн-калькулятор расчета значения F-критерия Фишера:

1-й вариант: на основе значения коэффициент (индекса) детерминации

2-й вариант: на основе сумм квадратов отклонений

Использование критерия Фишера для проверки значимости регрессионной модели

Критерий Фишера для регрессионной модели отражает, насколько хорошо эта модель объясняет общую дисперсию зависимой переменной. Расчет критерия выполняется по уравнению:

где R — коэффициент корреляции;
f₁ и f₂ — число степеней свободы.

Первая дробь в уравнении равна отношению объясненной дисперсии к необъясненной. Каждая из этих дисперсий делится на свою степень свободы (вторая дробь в выражении). Число степеней свободы объясненной дисперсии f₁ равно количеству объясняющих переменных (например, для линейной модели вида Y=A*X+B получаем f₁=1). Число степеней свободы необъясненной дисперсии f₂ = N—k-1, где N-количество экспериментальных точек, k-количество объясняющих переменных (например, для модели Y=A*X+B подставляем k=1).

Для проверки значимости уравнения регрессии вычисленное значение критерия Фишера сравнивают с табличным, взятым для числа степеней свободы f₁ (бóльшая дисперсия) и f₂ (меньшая дисперсия) на выбранном уровне значимости (обычно 0.05). Если рассчитанный критерий Фишера выше, чем табличный, то объясненная дисперсия существенно больше, чем необъясненная, и модель является значимой.

Коэффициент корреляции и F-критерий, наряду с параметрами регрессионной модели, как правило, вычисляются в алгоритмах, реализующих метод наименьших квадратов.

Видео:Эконометрика. Нелинейная регрессия: парабола.Скачать

Критерий Фишера и Стьюдента

С помощью критерия Фишера оценивают качество регрессионной модели в целом и по параметрам.

Для этого выполняется сравнение полученного значения F и табличного F значения. F-критерия Фишера. F фактический определяется из отношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы:

где n — число наблюдений;

m — число параметров при факторе х.

F табличный — это максимальное значение критерия под влиянием случайных факторов при текущих степенях свободы и уровне значимости а.

Уровень значимости а — вероятность не принять гипотезу при условии, что она верна. Как правило а принимается равной 0,05 или 0,01.

Если Fтабл > Fфакт то признается статистическая незначимость модели, ненадежность уравнения регрессии.

Видео:Эконометрика. Оценка значимости параметров уравнения регрессии. Критерий Стьюдента.Скачать

Таблицы по нахождению критерия Фишера и Стьюдента

Таблицы значений F-критерия Фишера и t-критерия Стьюдента Вы можете посмотреть здесь.

Табличное значение критерия Фишера вычисляют следующим образом:

1. Определяют k1, которое равно количеству факторов (Х). Например, в однофакторной модели (модели парной регрессии) k1=1, в двухфакторной k=2.
2. Определяют k2, которое определяется по формуле n — m — 1, где n — число наблюдений, m — количество факторов. Например, в однофакторной модели k2 = n — 2.
3. На пересечении столбца k1 и строки k2 находят значение критерия Фишера

Для нахождения табличного значения критерия Стьюдента определяют число степеней свободы, которое определяется по формуле n — m — 1 и находят его значение при определенном уровне значимости (0,10, 0,05, 0,01).

Видео:Однофакторная регрессионная модель. Коэффициенты детерминации, корреляции. Критерий ФишераСкачать

Критерии Стьюдента

Для оценки статистической значимости модели по параметрам рассчитывают t-критерии Стьюдента.

Оценка значимости модели с помощью критерия Стьюдента проводится путем сравнения их значений с величиной случайной ошибки:

Случайные ошибки коэффициентов линейной регрессии и коэффициента корреляции определяются по формулам:

Сравнивая фактическое и табличное значения t-статистики и принимается или отвергается гипотеза о значимости модели по параметрам.

Зависимость между критерием Фишера и значением t-статистики Стьюдента определяется так

Как и в случае с оценкой значимости уравнения модели в целом, модель считается ненадежной если tтабл > tфакт

Видео:Статистический метод (критерий): как выбрать для анализа?Скачать

Видео лекциий по расчету критериев Фишера и Стьюдента

Для более подробного изучения расчетов критериев Фишера и Стьюдента советуем посмотреть это видео

Лекция 1. Критерии и Гипотезы

Лекция 2. Критерии и Гипотезы

Лекция 3. Критерии и Гипотезы

Видео:Эконометрика. Нелинейная регрессия. Гипербола.Скачать

Определение доверительных интервалов

Для построения доверительного интервала определяется предельная ошибка А для обоих показателей:

Формулы для нахождения доверительных интервалов выглядят так

Прогнозное значение у определяется с помощью подстановки в
уравнение регрессии прогнозного значения х. Вычисляется средняя стандартная ошибка прогноза

и находится доверительный интервал

Задача регрессионного анализа в предмете эконометрика состоит в анализе дисперсии изучаемого показателя y:

общая сумма квадратов отклонений (TSS)

сумма квадратов отклонений, обусловленная регрессией (RSS)

остаточная сумма квадратов отклонений (ESS)

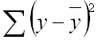
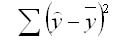
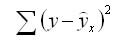
Долю дисперсии, обусловленную регрессией, в общей дисперсии показателя у характеризует коэффициент детерминации R, который должен превышать 50% (R 2 > 0,5). В контрольных по эконометрике в ВУЗах этот показатель рассчитывается всегда.

Любые задачи по эконометрике решаются здесь

🎬 Видео

Эконометрика. Нелинейная регрессия. Полулогарифмические функции.Скачать

Нелинейная регрессия в MS Excel. Как подобрать уравнение регрессии? Некорректное значение R^2Скачать

Эконометрика. Нелинейная регрессия. Степенная функция.Скачать

Множественная регрессия в ExcelСкачать

Регрессия в ExcelСкачать

Проверка гипотезы о нескольких линейных ограниченияхСкачать

2.7. Распределение Хи квадрат, Стьюдента, Фишера .Скачать

1.1 Нелинейная регрессия в ExcelСкачать

Множественная регрессияСкачать

#18. Линейный дискриминант Фишера | Машинное обучениеСкачать