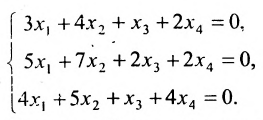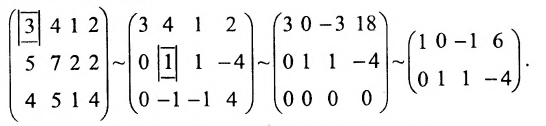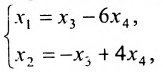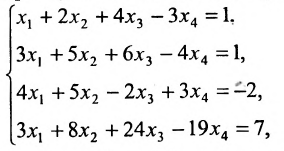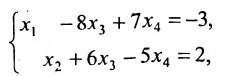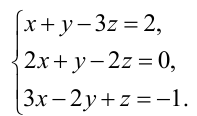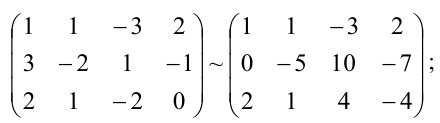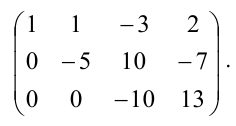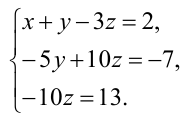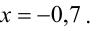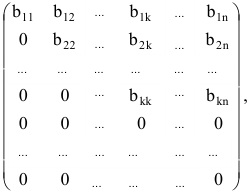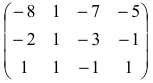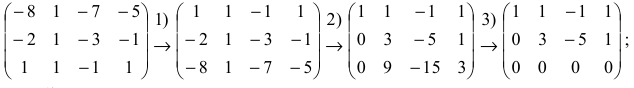Содержание:
Базисные и свободные переменные:
Пусть задана система
Элементарными преобразованиями системы линейных уравнений называются следующие преобразования:
- исключение из системы уравнения вида
- умножение обеих частей одного из уравнений системы на любое действительное число
;
- перестановка местами уравнений системы;
- прибавление к обеим частям одного из уравнений системы соответствующих частей другого уравнения, умноженных на любое действительное число не равное нулю.
Элементарные преобразования преобразуют данную систему уравнений в эквивалентную систему, т.е. в систему, которая имеет те же решения, что и исходная.
Для решения системы т линейных уравнений с т неизвестными удобно применять метод Гаусса, называемый методом последовательного исключения неизвестных, который основан на применении элементарных преобразований системы. Рассмотрим этот метод.
Предположим, что в системе (6.1.1)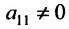
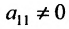
На первом шаге метода Гаусса исключим неизвестное 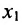
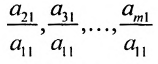
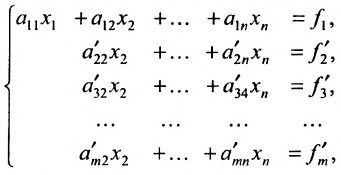
в которой коэффициенты 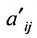
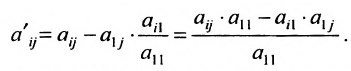
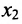
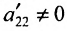
чтобы это условие было выполнено). Для исключения неизвестного 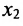
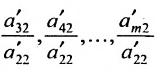
в которой коэффициенты 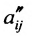
Продолжая аналогичные преобразования, систему (6.1.1) можно привести к одному из видов:
Совокупность элементарных преобразований, приводящих систему (6.1.1) к виду (6.1.4) или (6.1.5) называется прямым ходом метода Гаусса.
Отметим, что если на каком-то шаге прямого хода метода Гаусса получим уравнение вида:
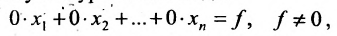
Итак, предположим, что в результате прямого хода метода Гаусса мы получили систему (6.1.4), которая называется системой треугольного вида. Тогда из последнего уравнения находим значение 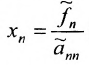
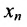
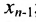
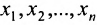
Если же в результате прямого хода метода Гаусса мы получим систему (6.1.5), которая называется системой ступенчатого вида, то из последнего уравнения этой системы находим значение неизвсстного 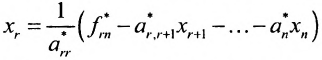
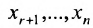
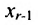
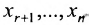
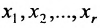
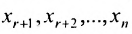
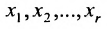
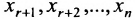
Таким образом, если система (6.1.1) путём элементарных преобразований приводится к треугольному виду (6.1.4), то она имеет единственное решение, если же она приводится к системе ступенчатого вида (6.1.5), то она имеет бесконечное множество решений. При этом неизвестные 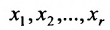
Практически удобнее преобразовывать не саму систему уравнений (6.1.1), а расширенную матрицу системы, соединяя последовательно получающиеся матрицы знаком эквивалентности
Формализовать метод Гаусса можно при помощи следующего алгоритма.
- Алгоритм решения системы m линейных уравнений с n неизвестными методом Гаусса
- Исследование совместности и определённости системы. Теорема Кронекера-Капелли
- Однородные системы линейных уравнений
- Фундаментальная система решений. Общее решение неоднородной системы линейных уравнений
- Определение метода Гаусса
- Вычисление метода Гаусса
- Общая теория систем линейных уравнений
- Условия совместности.
- Нахождение решений.
- Приведенная система.
- Общее решение системы линейных уравнений.
- Пример.
- Лекции по высшей математике, линейная алгебра (стр. 4 )
- 2. СИСТЕМЫ n ЛИНЕЙНЫХ УРАВНЕНИЙ С n НЕИЗВЕСТНЫМИ.
- 3. ОБЩИЕ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ.
- 🎥 Видео
Видео:Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Алгоритм решения системы m линейных уравнений с n неизвестными методом Гаусса
1. Составьте расширенную матрицу коэффициентов системы уравнений так, чтобы 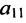
2. Выполните первый шаг метода Гаусса: в первом столбце начиная со второй строки, запишите нули, а все другие элементы вычислите по формуле
Матрица после первого шага примет вид
3. Выполните второй шаг метода Гаусса, предполагая, что 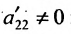
После второго шага матрица примет вид
4. Продолжая аналогичные преобразования, придёте к одному из двух случаев:
а) либо в ходе преобразований получим уравнение вида
тогда данная система несовместна;
б) либо придём к матрице вида:
где 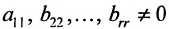
связано с тем, что в процессе преобразований матрицы исключаются строки, состоящие из нулей.
5. Использовав конечную матрицу, составьте систему, при этом возможны два случая:
Система имеет единственное,решение 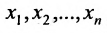
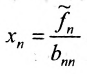
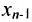
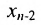
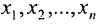
5.2. 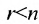
Тогда r неизвестных будут базисными, а остальные (n-r) — свободными. Из последнего уравнения выражаете неизвестное 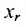
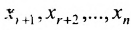
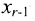
Система имеет в этом случае бесконечное множество решений.
Приведенный алгоритм можно несколько видоизменить и получить алгоритм полного исключения, состоящий в выполнении следующих шагов. На первом шаге:
- составляется расширенная матрица;
- выбирается разрешающий элемент расширенной матрицы
(если
, строки матрицы можно переставить так, чтобы выполнялось условие
);
- элементы разрешающей строки (строки, содержащей разрешающий элемент) оставляем без изменения; элементы разрешающего столбца (столбца, содержащего разрешающий элемент), кроме разрешающего элемента, заменяем нулями;
- все другие элементы вычисляем по правилу прямоугольника: преобразуемый элемент равен разности произведений элементов главной диагонали (главную диагональ образует разрешающий элемент и преобразуемый) и побочной диагонали (побочную диагональ образуют элементы, стоящие в разрешающей строке и разрешающем столбце):
— разрешающий элемент (см. схему).
Последующие шаги выполняем по правилам:
1) выбирается разрешающий элемент 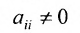
2) элементы разрешающей строки оставляем без изменения;
3) все элементы разрешающего столбца, кроме разрешающего элемента, заменяем нулями; • •
4) все другие элементы матрицы пересчитываем по правилу прямоугольника.
На последнем шаге делим элементы строк на диагональные элементы матрицы, записанные слева от вертикальной черты, и получаем решение системы.
Пример:
Решить систему уравнений:
Решение:
Составим расширенную матрицу системы, и применим алгоритм полного исключения, обозначая разрешающий элемент символом
Из последней матрицы находим следующее решение системы
уравнении:
Ответ:
Пример:
Решить систему уравнений:
Решение:
Составим расширенную матрицу системы, и применим алгоритм полного исключения, обозначая разрешающий элемент символом
Система привелась к ступенчатому виду (трапециевидной форме):
в которой неизвестные 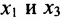
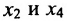
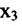
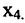
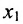
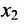
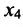
в котором 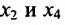
Если в общем решении положить 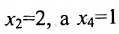
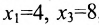
Ответ: система имеет бесконечное множество решений, общее решение которой записывается в виде:
Пример:
Решить систему уравнений:
Решение:
Составим расширенную матрицу системы, и применим алгоритм полного исключения, обозначая разрешающий элемент символом 
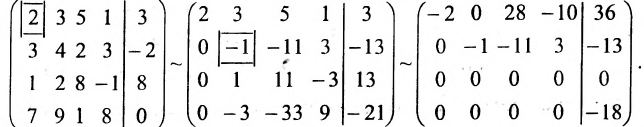
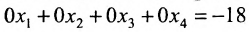
Ответ: система несовместна.
Замечание 1. Если дана система уравнений (6.1.1), в которой число уравнений m равно числу неизвестных n (m=n) и определитель этой системы 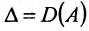
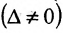
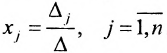
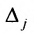
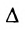
Если же такую систему (m-n) записать в матричной форме AX=F, то её решение можно найти по формуле 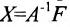
Замечание 2. Используя метод Гаусса, тем самым и алгоритм полного исключения, можно находить обратную матрицу. Для этого составляется расширенная матрица, в которой слева от вертикальной черты записана матрица А, а справа — единичная матрица. Реализовав алгоритм полного исключения, справа от вертикальной черты получаем обратную матрицу, а слева — единичную.
Пример:
Найти обратную матрицу для матрицы:
Решение:
то обратная матрица 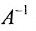
Покажем, что
ответ
Исследование совместности и определённости системы. Теорема Кронекера-Капелли
Рассмотрим систему (6.1.1) m линейных уравнений с n неизвестными при любых m и n (случай m=n не исключается). Вопрос о совместности системы решается следующим критерием.
Теорема 6.2.1. (критерий Кронкера-Капелли). Для того, чтобы система линейных уравнений(6.1.1) была совместна, необходимо и достаточно, чтобы ранг матрицы А системы был равен рангу расширенной матрицы 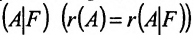
Доказательство и Необходимость:
Предположим, что система (6.1.1) совместна и 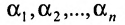
Из этих равенств следует, что последний столбец матрицы 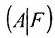
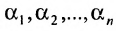
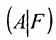
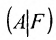
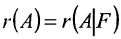
Достаточность. Пусть 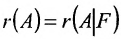
столбцов матрицы А, которые одновременно будут базисными столбцами и матрицы 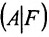
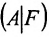
где 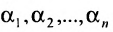
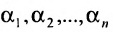
эта система совместна.
Совместная система линейных уравнений (6.1.1) может быть либо определенной, либо неопределенной.
Следующая теорема даст критерий определенности.
Теорема 6.2.2. Совместная система линейных уравнений имеет единственное решение тогда и только тогда, когда ранг матрицы А системы равен числу п ее неизвестных.
Таким образом, если число уравнений m системы (6.1.1) меньше числа ее неизвестных n и система совместна, то ранг матрицы системы 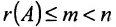
В случае 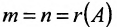
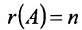
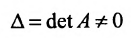
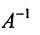
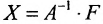
Следует отметить, что, решая систему (6.1.1) методом Гаусса, мы определяем и совместность, и определённость системы.
Пример:
Исследовать на совместность и определённость следующую систему линейных уравнений:
Решение:
Составим расширенную матрицу заданной системы. Определяя её ранг, находим тем самым и ранг матрицы системы. Для нахождения ранга матрицы применим алгоритм метода Гаусса.
Из последней матрицы следует, что ранг расширенной матрицы 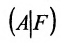
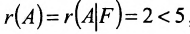
Однородные системы линейных уравнений
Система линейных уравнений (6.1.1) называется однородной, если все свободные члены 
Эта система всегда совместна, так как очевидно, что она имеет нулевое решение
Для однородной системы важно установить, имеет ли она ненулевые решения. Этот факт устанавливается следующей теоремой.
Теорема 6.3.1. Для того, чтобы однородная система имела ненулевые решения, необходимо и достаточно, чтобы ранг г матрицы А системы был меньше числа неизвестных n (r
Доказательство. Необходимость. Пусть система (6.3.1) имеет ненулевое решение. Тогда она неопределённая, т.к. имеет еще и нулевое решение. В силу теоремы 6.2.2 ранг матрицы неопределённой системы не может равняться n потому что при r(А)=n система определённая. Следовательно, 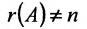
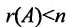
Достаточность. Если 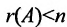
Следствие 1. Если число неизвестных в однородной системе больше числа уравнений, то однородная система имеет ненулевые решения.
Доказательство. Действительно, ранг матрицы системы (6.3.1) не может превышать m. Но так как по условию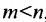
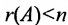
Следствие 2. Для того, чтобы однородная система с квадрат-ной матрицей имела ненулевые решения, необходимо и достаточно, чтобы её определитель 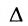
Доказательство. Рассмотрим однородную систему с квадратной матрицей:
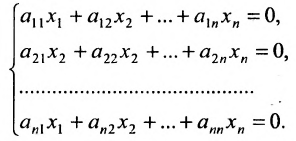
Если определитель матрицы системы 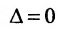
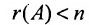
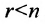
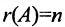
Пример:
Решить систему однородных линейных уравнений:
Решение:
Составим матицу системы и применим алгоритм полного исключения:
Из последней матрицы следует, что 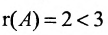
Используя последнюю матрицу, последовательно находим общее решение:
Неизвестные 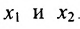
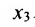
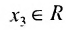
Фундаментальная система решений. Общее решение неоднородной системы линейных уравнений
Рассмотрим систему однородных линейных уравнений
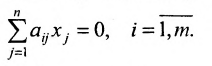
системы m линейных однородных уравнений с n неизвестными можно рассматривать как вектор-строку 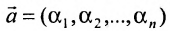
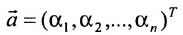
1) сумма двух решений также является решением системы, т.е.
если 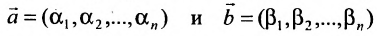
(6.4.1), то и 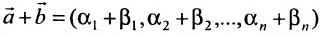
2) произведение решений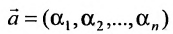
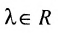
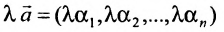
Из приведенных свойств следует, что
3) линейная комбинация решений системы (6.4.1) является решением этой системы.
В частности, если однородная система (6.4.1) имеет хотя бы одно ненулевое решение, то из него умножением на произвольные числа, можно получить бесконечное множество решений.
Определение 6.4.1. Фундаментальной системой решений для системы однородных линейных уравнений (6.4.1) называется линейно независимая система решений, через которую линейно выражается любое решение системы (6.4.1).
Заметим, что если ранг матрицы системы (6.4.1) равен числу неизвестных n (r(А)=n), то эта система не имеет фундаментальной системы решений, так как единственным решением будет нулевое решение, составляющее линейно зависимую систему. Существование и число фундаментальных решений определяется следующей теоремой.
Теорема 6.4.1. Если ранг матрицы однородной системы уравнений (6.4.1) меньше числа неизвестных (r(А)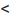
Сформулируем алгоритм построения фундаментальной системы решений:
- Выбираем любой определитель
порядка n-r, отличный от нуля, в частности, определитель порядка n-r, у которого элементы главной диагонали равны единице, а остальные — нули.
- Свободным неизвестным придаём поочерёдно значения, равные элементам первой, второй и т.д. строк определителя
, и каждый раз из общего решения находим соответствующие значения базисных неизвестных.
- Из полученных n-r решений составляют фундаментальную систему решений.
Меняя произвольно определитель 
Пример:
Найти общее решение и фундаментальную систему решений для однородной системы уравнений:
Решение:
Составим матрицу системы и применим алгоритм полного исключения.
Для последней матрицы составляем систему:
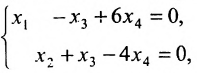
, из которой находим общее решение:
в котором 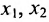
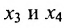
Построим фундаментальную систему решений. Для этого выбираем определитель 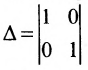
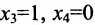
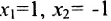
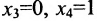
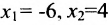
Таким образом, построенные два решения (1; -1; 1; 0) и (-6; 4; 0; 1) составляют фундаментальную систему решений.
Если ранг матрицы системы однородных линейных уравнений (6.4.1) на единицу меньше числа неизвестных: 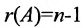
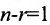
Рассмотрим теперь неоднородную систему m линейных уравнений с n неизвестными (6.1.1). Если в системе (6.1.1) положить 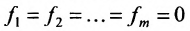
Решения системы (6.1.1) и её приведенной системы удовлетворяют свойствам:
- Сумма и разность любого решения системы (6.1.1) и любого решения её приведенной системы является решением неоднородной системы.
- Все решения неоднородной системы можно получить, прибавляя к одному (любому) её решению поочерёдно все решения её приведенной системы.
Из этих свойств следует теорема.
Теорема 6.4.2. Общее решение неоднородной системы (6.1.1.) определяется суммой любого частного решения этой системы и общего решения её приведенной системы.
Пример:
Найти общее решение системы:
Решение:
Составим расширенную матрицу (A|F) заданной системы и применим алгоритм полного исключения:
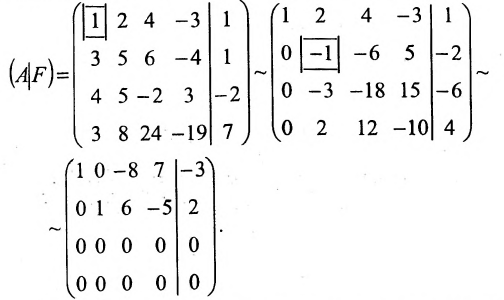
Преобразованной матрице соответствует система уравнений:
из которой находим общее решение системы:
, где 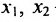
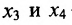
Покажем, что это общее решение определяется суммой любого частного решения заданной системы и общего решения приведенной системы.
Подставляя вместо свободных неизвестных 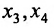
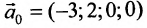
Очевидно, что общее решение приведенной системы имеет вид:
Суммируя частное решение заданной системы и общее решение приведенной системы, получим общее решение (6.4.2) исходной системы.
Отметим, что общее решение системы (6.1.1) можно представить в векторном виде:
где 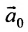
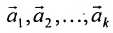
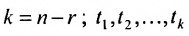
Формула (6.4.4) называется общим решением системы (6.1.1) в векторной форме.
Запишем общее решение системы примера 6.4.1 в векторной форме. Для этого определим фундаментальную систему решений приведенной системы. Возьмём определитель 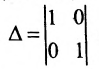
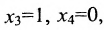
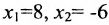
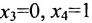
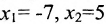
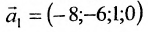
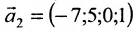
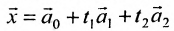
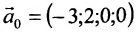
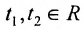
Видео:15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

Определение метода Гаусса
Исторически первым, наиболее распространенным методом решения систем линейных уравнений является метод Гаусса, или метод последовательного исключения неизвестных. Сущность этого метода состоит в том, что посредством последовательных исключений неизвестных данная система превращается в ступенчатую (в частности, треугольную) систему, равносильную данной. При практическом решении системы линейных уравнений методом Гаусса удобнее приводить к ступенчатому виду не саму систему уравнений, а расширенную матрицу этой системы, выполняя элементарные преобразования над ее строками. Последовательно получающиеся в ходе преобразования матрицы обычно соединяют знаком эквивалентности.
Пример:
Решить систему уравнений методом Гаусса:
Решение:
Выпишем расширенную матрицу данной системы 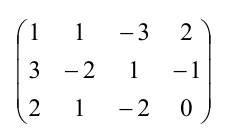
а) из ее второй и третьей строк вычтем первую, умноженную соответственно на 3 и 2:
б) третью строку умножим на (-5) и прибавим к ней вторую:
В результате всех этих преобразований данная система приводится к треугольному виду:
Из последнего уравнения находим 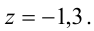
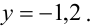
Видео:Решение системы уравнений методом ГауссаСкачать

Вычисление метода Гаусса
Этот метод основан на следующей теореме.
Теорема:
Элементарные преобразования не изменяют ранга матрицы.
К элементарным преобразованиям матрицы относят:
- перестановку двух параллельных рядов;
- умножение какого-нибудь ряда на число, отличное от нуля;
- прибавление к какому-либо ряду матрицы другого, параллельного ему ряда, умноженного на произвольное число.
Путем элементарных преобразований исходную матрицу можно привести к трапециевидной форме
где все диагональные элементы 
Пример:
Найти ранг матрицы
1) методом окаймляющих миноров;
2 ) методом Гаусса.
Указать один из базисных миноров.
Решение:
1. Найдем ранг матрицы методом окаймляющих миноров. Выберем минор второго порядка, отличный от нуля. Например,
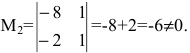
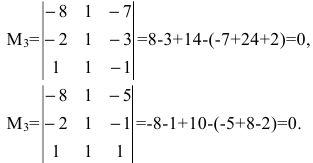
2. Найдем ранг матрицы методом Гаусса. Производя последовательно элементарные преобразования, получим:
- переставили первую и третью строки;
- первую строку умножили на 2 и прибавили ко второй, первую строку умножили на 8 и прибавили к третьей;
- вторую строку умножили на -3 и прибавили к третьей.
Последняя матрица имеет трапециевидную форму и ее ранг равен двум. Следовательно, ранг исходной матрицы также равен двум.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Прямая линия на плоскости и в пространстве
- Плоскость в трехмерном пространстве
- Функция одной переменной
- Производная функции одной переменной
- Дифференциальные уравнения с примерами
- Обратная матрица — определение и нахождение
- Ранг матрицы — определение и вычисление
- Определители второго и третьего порядков и их свойства
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Общая теория систем линейных уравнений
Видео:Решение системы уравнений методом обратной матрицы - bezbotvyСкачать

Условия совместности.
Займемся изучением систем из m уравнений с n неизвестными. Систему
begina_^x^+a_^x^+. +a_^x^=b^,\a_^x^+a_^x^+. +a_^x^=b^,\cdots\a_^x^+a_^x^+. +a_^x^=b^end мы можем кратко записать в виде tag Aboldsymbol=boldsymbol.
Система задается своей расширенной матрицей A^ , получаемой объединением матрицы системы A и столбца свободных членов boldsymbol .
Простое и эффективное условие, необходимое и достаточное для совместности системы (1) , дает следующая теорема, называемая теоремой Кронекера-Капелли.
Система линейных уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы.
Иначе утверждение теоремы можно сформулировать так: приписывание к матрице A размеров m times n столбца boldsymbol высоты m не меняет ее ранга тогда и только тогда, когда этот столбец — линейная комбинация столбцов A .
Если mathbf,A^ = mathbf,A , то базисный минор A является базисным и для A^ . Следовательно, boldsymbol раскладывается по базисным столбцам A . Мы можем считать его линейной комбинацией всех столбцов A , добавив недостающие столбцы с нулевыми коэффициентами.
Обратно, если boldsymbol раскладывается по столбцам A , то элементарными преобразованиями столбцов можно превратить A^ в матрицу A_ , получаемую из A приписыванием нулевого столбца. Из утверждения о том, что ранг матрицы не меняется при элементарных преобразованиях, следует mathbf,A_ = mathbf,A^ . С другой стороны, mathbf,A_ = mathbf,A , так как добавление нулевого столбца не может создать новых невырожденных подматриц. Отсюда mathbf,A = mathbf,A^ , как и требовалось.
Иначе это утверждение можно сформулировать так.
Система линейных уравнений несовместна тогда и только тогда, когда противоречивое равенство 0=1 является линейной комбинацией ее уравнений.
Равенство рангов матрицы системы и расширенной матрицы можно выразить, понимая ранг матрицы как строчный ранг. Это приведет нас к важной теореме, известной как теорема Фредгольма.
Транспонируем матрицу A системы (1) и рассмотрим систему из n линейных уравнений tag begin a_^y_+a_^y_+. +a_^y_=0,\ a_^y_+a_^y_+. +a_^y_=0,\cdots\a_^y_+a_^y_+. +a_^y_=0end с m неизвестными, матрицей A^ и свободными членами, равными нулю. Она называется сопряженной однородной системой для системы (1) . Если boldsymbol — столбец высоты m из неизвестных, то систему (2) можно записать как A^ boldsymbol=boldsymbol , или лучше в виде tag boldsymbol^A=boldsymbol, где boldsymbol — нулевая строка длины n .
Для того чтобы система (1) была совместна, необходимо и достаточно, чтобы каждое решение сопряженной однородной системы (3) удовлетворяло уравнению tag boldsymbol^ boldsymbol=y_b^+. +y_b^=0.
1^ . Пусть система (1) совместна, то есть существует столбец boldsymbol высоты n , для которого Aboldsymbol=boldsymbol . Тогда для любого столбца boldsymbol высоты m выполнено boldsymbol^ Aboldsymbol=boldsymbol^ boldsymbol . Если boldsymbol — решение системы (3) , то boldsymbol^ boldsymbol=(boldsymbol^ A)boldsymbol=boldsymbolboldsymbol=0 .
2^ . Предположим теперь, что система (1) несовместна. Тогда согласно утверждению 1 строка begin 0&. & 0& 1 end входит в упрощенный вид расширенной матрицы A^=begin A& |& boldsymbol end и, следовательно, является линейной комбинацией ее строк. Обозначим коэффициенты этой линейной комбинации y_. y_ и составим из них столбец boldsymbol . Для этого столбца boldsymbol^ begin A& |& boldsymbol end=begin 0&. & 1 end (согласно данного утверждения). Это же равенство можно расписать как два: boldsymbol^ A=boldsymbol и boldsymbol^ boldsymbol=1 . Итак, нам удалось найти решение системы (3) , не удовлетворяющее условию (4) . Это заканчивает доказательство.
В качестве примера применим теорему Фредгольма к выводу условия параллельности двух различных прямых на плоскости. Их уравнения составляют систему A_x+B_y+C_=0, A_x+B_y+C_=0.
Она не имеет решений, если существуют такие числа y_, y_ , что y_A_+y_A_=0 , y_B_+y_B_=0 , но y_C_+y_C_ neq 0 . Ясно, что y_ и y_ не равны нулю. Поэтому можно положить lambda=-y_/y_ и записать полученное условие в виде: существует число lambda такое, что A_=lambda A_ , B_=lambda B_ и C_ neq lambda C_ .
Видео:Лекция 13. Исследование систем линейных уравнений. Теорема Кронекера — Капелли.Скачать

Нахождение решений.
В этом пункте мы будем предполагать, что дана совместная система из m линейных уравнений с n неизвестными. Ранг матрицы системы обозначим r . Поскольку ранг расширенной матрицы тоже равен r , мы можем считать базисные столбцы матрицы системы базисными столбцами расширенной матрицы. Элементарными преобразованиями строк приведем расширенную матрицу к упрощенному виду (возможность этого мы уже доказывали). Наша система линейных уравнений перейдет в эквивалентную ей систему из r линейно независимых уравнений.
Для удобства записи будем предполагать, что первые r столбцов — базисные. Тогда преобразованную систему можно записать в виде tag begin x^=beta^-(alpha_^x^+. +alpha_^x^),\cdots\x^=beta^-(alpha_^x^+. +alpha_^x^).end
Здесь alpha_^ и beta^ — элементы преобразованной расширенной матрицы. В левых частях равенств мы оставили неизвестные, соответствующие выбранным нами базисным столбцам, так называемые базисные неизвестные. Остальные неизвестные, называемые параметрическими, перенесены в правые части равенств.
Как бы мы ни задали значения параметрических неизвестных, по формулам (5) мы найдем значения базисных так, что они вместе со значениями параметрических неизвестных образуют решение системы (1) . Легко видеть, что так мы получим все множество решений.
На формулах (5) можно было бы и остановиться, но ниже мы дадим более простое и наглядное, а также принципиально важное описание совокупности решений системы линейных уравнений.
Видео:12. Метод Гаусса решения систем линейных уравнений. Часть 1.Скачать

Приведенная система.
Сопоставим системе линейных уравнений (1) однородную систему с той же матрицей коэффициентов: tagAboldsymbol=boldsymbol. По отношению к системе (1) она называется приведенной.
Пусть boldsymbol_ — решение системы (1) . Столбец boldsymbol также будет ее решением тогда и только тогда, когда найдется такое решение у приведенной системы (6) , что boldsymbol=boldsymbol_+boldsymbol .
Пусть boldsymbol — решение системы (1) . Рассмотрим разность boldsymbol=boldsymbol-boldsymbol_ . Для нее Aboldsymbol=Aboldsymbol-Aboldsymbol_=boldsymbol-boldsymbol=boldsymbol .
Обратно, если boldsymbol — решение системы (6) , и boldsymbol=boldsymbol_+boldsymbol , то Aboldsymbol=Aboldsymbol_+Aboldsymbol=boldsymbol+boldsymbol=boldsymbol .
Это предложение сводит задачу описания множества решений совместной системы линейных уравнений к описанию множества решений ее приведенной системы.
Однородная система совместна. Действительно, нулевой столбец является ее решением. Это решение называется тривиальным.
Пусть столбцы матрицы A линейно независимы, то есть mathbf,A=n . Тогда система (6) имеет единственное решение (ранее мы это уже доказывали) и, следовательно, нетривиальных решений не имеет.
Если boldsymbol_ и boldsymbol_ — решения однородной системы, то любая их линейная комбинация — также решение этой системы.
Действительно, из Aboldsymbol_=boldsymbol и Aboldsymbol_=boldsymbol для любых alpha и beta следует A(alpha boldsymbol_+beta boldsymbol_)=alpha A boldsymbol_+beta Aboldsymbol_=boldsymbol .
Если однородная система имеет нетривиальные решения, то можно указать несколько линейно независимых решений таких, что любое решение является их линейной комбинацией. Сделаем это.
Матрица F , состоящая из столбцов высоты n , называется фундаментальной матрицей для однородной системы с матрицей А, если:
- AF=O ;
- столбцы F линейно независимы;
- ранг F максимален среди рангов матриц, удовлетворяющих условию 1).
Столбцы фундаментальной матрицы называются фундаментальной системой решений.
Если фундаментальная матрица существует, то каждый ее столбец в силу первого условия определения — решение системы. Если система не имеет нетривиальных решений, то фундаментальной матрицы нет. Это будет в том случае, когда столбцы А линейно независимы: mathbf,A=n .
Ниже мы докажем, что в остальных случаях фундаментальная матрица существует, но сначала выясним, что означает третье условие в определении.
Пусть A — матрица размеров m times n и ранга r . Если AF=O , то mathbf,F leq n-r .
Приведем матрицу A к упрощенному виду элементарными преобразованиями строк, а затем элементарными преобразованиями столбцов обратим в нулевые все небазисные столбцы. Мы получим матрицу A’=PAQ , где P и Q — произведения соответствующих элементарных матриц. Первые r строк A’ — строки единичной матрицы порядка n , а остальные — нулевые. Обозначим F’=Q^F . Тогда mathbf,F’ = mathbf,F . Используя ранее доказанное нами утверждение, легко заметить, что первые r строк матрицы A’F’ совпадают с первыми r строками F’ . Но A’F’=PAF=O и, следовательно, F’ содержит r нулевых строк. Так как всего в ней n строк, mathbf,F’ leq n-r . Это равносильно доказываемому утверждению.
Покажем теперь, как может быть построена фундаментальная матрица. Согласно ранее доказанному утверждению, решение однородной системы состоит из коэффициентов равной нулю линейной комбинации столбцов матрицы системы. Мы можем получить такие линейные комбинации, основываясь на теореме о базисном миноре. Снова для удобства записи будем считать, что в матрице A первые r столбцов — базисные. Каждый из небазисных столбцов boldsymbol_ (j=r+1. n) раскладывается по базисным: tag boldsymbol_=alpha_^boldsymbol_+. +alpha_^boldsymbol_. Отсюда следует, что столбец begin -alpha_^. -alpha_^& 0. 0& 1& 0. 0 end^ решением. (Единица в нем стоит на j -м месте.)
Таких решений можно составить столько, сколько есть небазисных столбцов, то есть (n-r) . Убедимся в том, что эти решения линейно независимы. Для этого объединим все столбцы в одну матрицу tag begin -alpha_^& -alpha_^&. -alpha_^,\cdots\-alpha_^& -alpha_^&. -alpha_^,\1& 0&. & 0\0& 1&. & 0\cdots\0& 0&. & 1end.
Подматрица в последних n-r строках — единичная. Поэтому ранг матрицы (8) равен числу столбцов, и столбцы линейно независимы.
Таким образом, мы получили
Если ранг матрицы однородной системы линейных уравнений r меньше числа неизвестных n , то система имеет фундаментальную матрицу из n-r столбцов.
Итак, система столбцов (8) — фундаментальная система решений. Она называется нормальной фундаментальной системой решений. Каждому выбору базисных столбцов соответствует своя нормальная фундаментальная система решений. Вообще же, каждая система из n-r линейно независимых решений является фундаментальной.
Для нахождения матрицы (8) можно привести матрицу A системы к упрощенному виду, что даст коэффициенты разложения небазисных столбцов по базисным.
Пусть F — фундаментальная матрица системы Aboldsymbol=boldsymbol . Рассмотрим произвольный столбец с высоты n-r . Произведение Fboldsymbol — столбец высоты n , и из равенства AFboldsymbol =boldsymbol следует, что при любом с столбец Fboldsymbol — решение системы. Оказывается, имеет место
Столбец boldsymbol — решение системы Aboldsymbol=boldsymbol тогда и только тогда, когда существует такой столбец boldsymbol , что tag boldsymbol=Fboldsymbol.
Остается доказать необходимость условия. Пусть boldsymbol — решение. Присоединив его к F , получим матрицу F^=begin F | boldsymbol end . Эта матрица удовлетворяет условию AF^=O , так как каждый ее столбец — решение. Значит, mathbf,F^=n-r . По теореме Кронекера-Капелли мы заключаем отсюда, что существует столбец boldsymbol , удовлетворяющий системе Fboldsymbol=boldsymbol .
Видео:Линейная алгебра. Алексей Савватеев и Александр Тонис. Лекция 13.4. Существов. и единств. решения ДУСкачать

Общее решение системы линейных уравнений.
Теперь мы можем собрать воедино наши результаты — утверждения 2 и 6.
Выражение, стоящее в правой части формулы (10) , называется общим решением системы линейных уравнений. Если boldsymbol_. boldsymbol_ — фундаментальная система решений, а c_. c_ — произвольные постоянные, то формула (10) может быть написана так: tag boldsymbol=boldsymbol_+c_boldsymbol_+. +c_boldsymbol_.
Теорема 3 верна, в частности, и для однородных систем. Если boldsymbol_ — тривиальное решение, то (10) совпадает с (9) .
Одна из ранее доказанных нами теорем гласит, что для существования единственного решения системы из n линейных уравнений с n неизвестными достаточно, чтобы матрица системы имела детерминант, отличный от нуля. Сейчас легко получить и необходимость этого условия.
Пусть A — матрица системы из n линейных уравнений с n неизвестными. Если det A=0 , то система либо не имеет решения, либо имеет бесконечно много решений.
Равенство det A=0 означает, что mathbf,A и, следовательно, приведенная система имеет бесконечно много решений. Если данная система совместна, то из теоремы 3 следует, что и она имеет бесконечно много решений.
Видео:Решение системы уравнений методом обратной матрицы.Скачать

Пример.
Рассмотрим уравнение плоскости как систему tagAx+By+Cz+D=0 из одного уравнения. Пусть A neq 0 и потому является базисным минором матрицы системы. Ранг расширенной матрицы 1, значит, система совместна. Одно ее решение можно найти, положив параметрические неизвестные равными нулю: y=z=0 . Мы получим x=-D/A . Так как n=3 , r=1 , фундаментальная матрица имеет два столбца. Мы найдем их, придав параметрическим неизвестным два набора значений: y=1 , z=0 и y=0 , z=1 . Соответствующие значения базисной неизвестной x , найденные из приведенной системы, будут -B/A и -C/A . Итак, общее решение системы (12) tag begin x\ y\ z end=begin -D/A\ 0\ 0 end+c_ begin -B/A\ 1\ 0 end+c_ begin -C/A\ 0\ 1 end.
Выясним геометрический смысл полученного решения. Очевидно, прежде всего, что решение begin -D/A& 0& 0 end^ состоит из координат некоторой (начальной) точки плоскости, или, что то же, из компонент ее радиус-вектора. В формуле (10) решение x_0 можно выбирать произвольно. Это соответствует произволу выбора начальной точки плоскости. Мы уже знаем, что компоненты лежащих в плоскости векторов удовлетворяют уравнению Aalpha_+Balpha_+Calpha_=0 , то есть приведенной системе. Два линейно независимых решения этой системы (фундаментальная система решений) могут быть приняты за направляющие векторы плоскости. Таким образом, формула (13) — не что иное, как параметрические уравнения плоскости.
Видео:Матричный метод решения систем уравненийСкачать

Лекции по высшей математике, линейная алгебра (стр. 4 )
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 |
Запишем в разных видах систему уравнений 



x 1 


Вектор`x * = 
Система уравнений называется совместной, если она имеет хотя бы одно решение.
Система уравнений называется несовместной, если она не имеет ни одного решения.
Система уравнений называется определенной, если она имеет ровно одно решение.
Система уравнений называется неопределенной, если она имеет более одного решения.
Видео:Система линейных уравнений. Общее решение. Метод ГауссаСкачать

2. СИСТЕМЫ n ЛИНЕЙНЫХ УРАВНЕНИЙ С n НЕИЗВЕСТНЫМИ.
Квадратная матрица A называется невырожденной, если ее строки линейно независимы.
Согласно этому определению, свойствам определителей, критерию существования обратной матрицы получаем, что невырожденная матрица имеет ненулевой определитель и обладает обратной матрицей.
Благодаря этим свойствам имеем два особых метода решения системы A`x =`b с квадратной невырожденной матрицей A.
МАТРИЧНЫЙ МЕТОД РЕШЕНИЯ СЛУ.
Если матрица A системы A`x =`b квадратная невырожденная, то существует единственное решение`x * этой системы, равное произведению обратной матрицы A– 1 на столбец свободных членов`b, `x * = A– 1`b.
Докажем сначала, что вектор`x * является решением системы A`x =`b. В самом деле, A`x * = A · A– 1`b = E`b =`b, то есть A`x * =`b и`x * является решением системы A`x =`b.
Докажем теперь единственность этого решения. Предположим, что имеется еще другое решение`x 1, то есть A`x 1 =`b — верное равенство. Домножим обе части этого равенства слева на A– 1. Получим A– 1 A`x 1 = A– 1`b и, следовательно,`x 1 = A– 1`b, то есть`x 1 =`x *. Теорема доказана.
Таким образом, матричный метод решения системы A`x =`b с квадратной невырожденной матрицей A состоит в нахождении решения этой системы по формуле`x * = A– 1`b.
Если матрица A системы A`x =`b квадратная невырожденная, то существует единственное решение`x * = 



ПРИМЕР решения системы линейных уравнений по правилу Крамера.

D = 





Видео:Математика без Ху!ни. Метод Гаусса.Скачать

3. ОБЩИЕ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ.
Рассмотрим систему уравнений A`x =`b с произвольной матрицей A. Исследуем вопрос о ее совместности и количестве решений.
ТЕОРЕМА КРОНЕКЕРА – КАПЕЛЛИ.
Для того, чтобы система уравнений A`x =`b была совместной, необходимо и достаточно, чтобы ранг матрицы этой системы равнялся рангу ее расширенной матрицы.
1) Пусть система уравнений A`x =`b является совместной. Докажем, что ранг r A матрицы A равняется рангу r à расширенной матрицы Ã.
Представим матрицы A и Ã как системы их векторов столбцов
соответственно. Ранг матрицы A равен рангу системы векторов (1), а ранг матрицы Ã равен рангу системы векторов (2). Поскольку система векторов (1) является подсистемой системы векторов (2), то r A £ r Ã.
Так как система A`x =`b является совместной, то существует вектор `x * = 
`A 1,`A 2 , … ,`A n ,`b Î L (`A 1,`A 2 , … ,`A n ). По свойствам ранга системы векторов r à £ r A. Но так как r A £ r à , то r A = r à .
2) Пусть теперь r A = r à = r. Докажем, что система A`x =`b является совместной. Согласно определению базиса системы векторов базисы систем (1) и (2) содержат по r векторов. Пусть`A 1, `A 2 , … ,`A r — базис системы (1). Тогда эти же векторы будут являться и базисом системы (2). Действительно, векторы`A 1,`A 2 , … ,`A r образуют линейно независимую подсистему системы (2), а поскольку их количество совпадает с рангом системы (2), то они являются базисом этой системы. Следовательно, вектор`b можно представить в виде линейной комбинации векторов`A 1,`A 2 , …,`A r :
`b = l 1`A 1 + l 2`A 2 + … + l r`A r, а также в виде линейной комбинации
`b = l 1`A 1 + l 2`A 2 + … + l r`A r + 0`A r + 1 + … + 0`A n. Справедливость последнего равенства означает, что вектор`x *, координатами которого являются числа l 1, l 2 , … , l r , 0, … , 0 является решением системы уравнений A`x =`b, то есть система A`x =`b совместна. Теорема доказана.
ТЕОРЕМА ОБ ОПРЕДЕЛЕННОСТИ СЛУ.
Пусть система уравнений A`x =`b является совместной, имеет n неизвестных и r A = r à = r.
🎥 Видео
Базисные решения систем линейных уравнений (01)Скачать

2.2. Системы линейных уравнений. Метод обратной матрицы. Метод Крамера. Метод ГауссаСкачать

Система линейных уравнений. Метод обратной матрицы. Матричный метод.Скачать

Неоднородная система линейных уравненийСкачать

Решение системы уравнений методом Крамера.Скачать

10. Метод Крамера решения систем линейных уравнений.Скачать

9. Метод обратной матрицы для решения систем линейных уравнений / матричный методСкачать

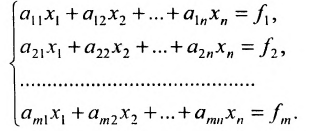
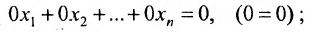
 ;
;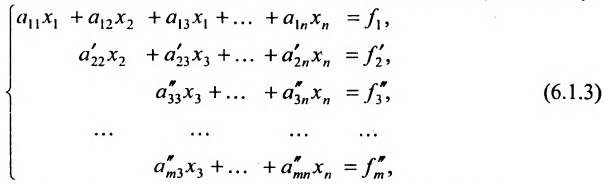
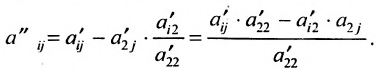
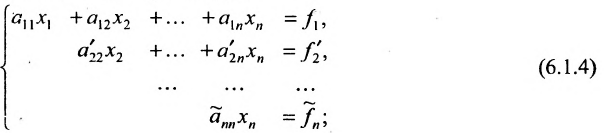
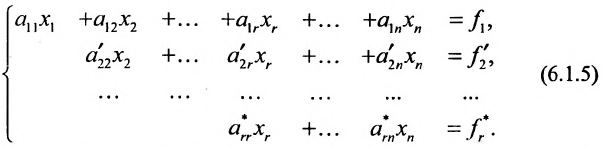

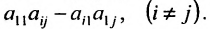
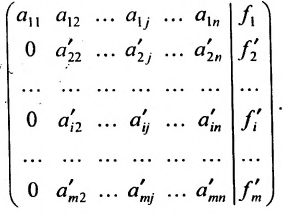
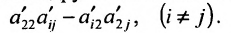

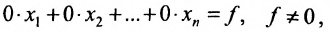
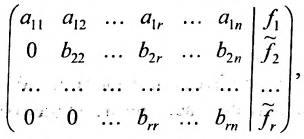
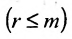
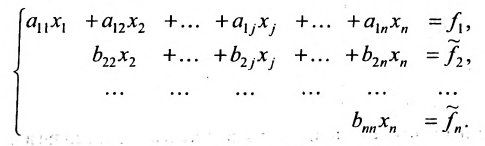
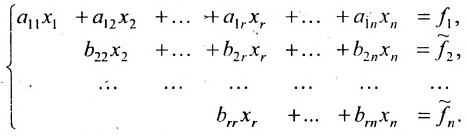
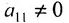 (если
(если 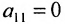 , строки матрицы можно переставить так, чтобы выполнялось условие
, строки матрицы можно переставить так, чтобы выполнялось условие 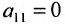 );
);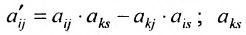 — разрешающий элемент (см. схему).
— разрешающий элемент (см. схему).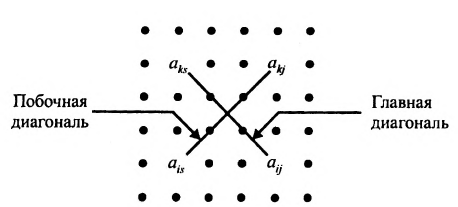
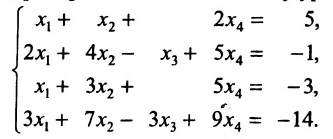


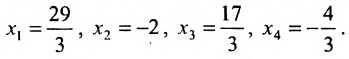
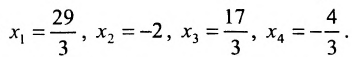
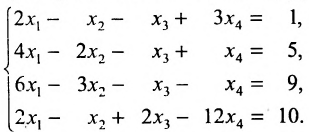

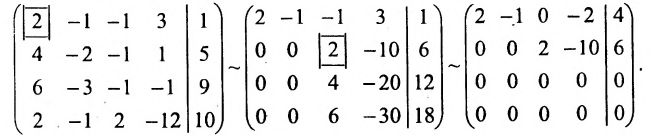

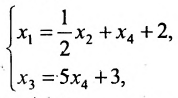
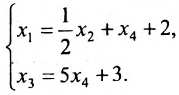
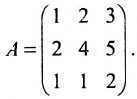
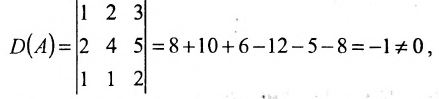

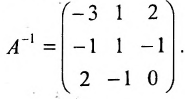
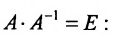
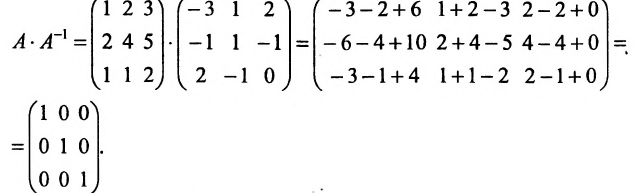
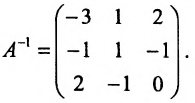
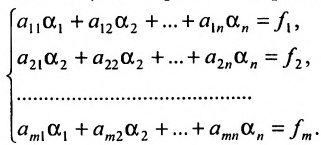
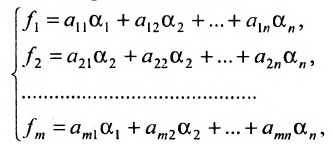
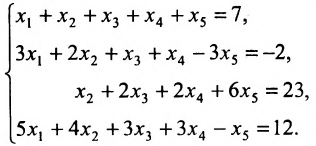

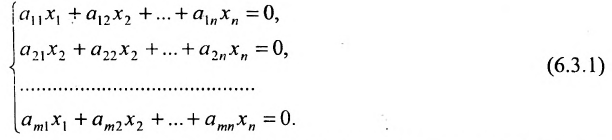
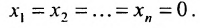
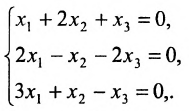
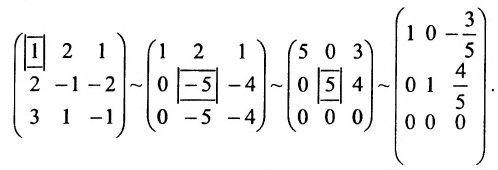
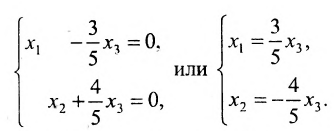
 порядка n-r, отличный от нуля, в частности, определитель порядка n-r, у которого элементы главной диагонали равны единице, а остальные — нули.
порядка n-r, отличный от нуля, в частности, определитель порядка n-r, у которого элементы главной диагонали равны единице, а остальные — нули. , и каждый раз из общего решения находим соответствующие значения базисных неизвестных.
, и каждый раз из общего решения находим соответствующие значения базисных неизвестных.