Применяя общие законы физики, можно составить дифференциальные уравнения для конвективного теплообмена, учитывающие как тепловые, так и гидродинамические явления в любом процессе.
Система дифференциальных уравнений состоит из 6 уравнений: энергии (или теплопроводности), теплообмена, движения (3 уравнения) и уравнение сплошности.
В результате анализа этих уравнений получены критерии подобия и критериальные уравнения, которые используются при исследовании конвективного теплообмена.
Критериальным уравнением называют зависимость между каким-либо определяемым критерием подобия и другими определяющими критериями подобия.
При расчете тепловых аппаратов искомыми величинами являются коэффициент теплоотдачи 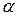
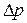
Критерий Нуссельта (Nu) содержит искомый коэффициент теплоотдачи 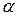
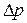
При конвективном теплообмене критериальные уравнения могут быть представлены в следующем виде:
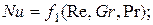
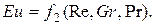
Зависимость между критериями в основном определяется опытным путем.
В случае вынужденного движения жидкости и при развитом турбулентном режиме свободная конвекция в сравнении с вынужденной очень мала, поэтому критериальное уравнение теплоотдачи упрощается:
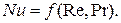
Для некоторых газов величина критерия Прандтля в процессе конвективного теплообмена почти не изменяется с температурой, поэтому критериальное уравнение принимает более простой вид:
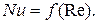
При свободном движении жидкости, когда вынужденная конвекция отсутствует, вместо критерия Рейнольдса в критериальное уравнение теплоотдачи необходимо ввести критерий Грасгофа. При этом получается зависимость:
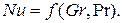
При исследовании теплообмена капельных жидкостей и газов со стенкой оказывается, что теплоотдача будет различной в условиях нагревания и охлаждения. Это явление связано с изменением физических параметров жидкости в пограничном слое. Для получения критериальных уравнений, одинаково справедливых как для нагревания, так и для охлаждения, вводят дополнительно отношения:
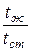
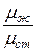
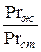
Первое соотношение обычно применяют при расчете теплоотдачи газов, остальные два – при расчете теплоотдачи капельных жидкостей.
Академик М.А. Михеев рекомендует учитывать направление теплового потока отношением 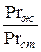
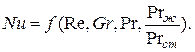
В такой же форме можно представить все уравнения для частных случаев. Количественная связь между критериями подобия и является предметом экспериментальных исследований.
Вопросы для самоконтроля к разделу 4
1. Что называется конвективным теплообменом?
2. Какие различают виды конвекции?
3. Гидродинамический и тепловой пограничные слои и их физический смысл.
4. Какие встречаются виды движения жидкости и их различие?
5. Критерий Рейнольдса и его обозначение.
6. Какова размерность критерия Рейнольдса?
7. Критическое значение критерия Рейнольдса.
8. Каков механизм передачи теплоты при ламинарном и турбулентном движении
9. Дать определение динамической и кинематической вязкости.
10. Какие факторы влияют на конвективный теплообмен?
11. Определение коэффициента теплоотдачи.
12. Функцией каких величин является коэффициент теплоотдачи?
13. Что называется условиями однозначности?
14. Почему для определения коэффициента теплоотдачи применяют теорию
15. Какие условия лежат в основе теории подобия?
16. От каких величин зависит коэффициент теплоотдачи?
17. Какие критерии подобия получают из дифференциальных уравнений
18. Какое уравнение называется критериальным?
19. Какими критериями подобия характеризуется конвективный теплообмен
Видео:Основы теории подобияСкачать

Теория подобия и критериальные уравнения
Конвективный теплообмен описывается системой дифференциальных уравнений и условиями однозначности с большим количеством переменных. Попытки аналитического решения полной системы уравнений наталкиваются на серьезные трудности. Поэтому большое значение приобретает экспериментальный путь исследования. Однако при изучении столь сложного процесса, как конвективный теплообмен, не всегда легко проводить и опытное исследование.
Для исследования влияния на процесс какой-либо одной величины остальные нужно сохранять неизменными, что не всегда возможно или затруднительно из-за большого количества переменных. Кроме того, нужно быть уверенным, что результаты, получаемые с помощью какой-либо конкретной установки (модели), можно перенести и на другие аналогичные процессы (образец). Эти трудности помогает разрешить теория подобия. С помощью теории подобия размерные физические величины можно объединить в безразмерные комплексы, причем так, что число комплексов будет меньше числа величин. Полученные безразмерные комплексы можно рассматривать как новые переменные.
При введении в уравнения безразмерных комплексов число величин под знаком искомой функции формально сокращается, что упрощает исследование физических процессов.
Теория подобия устанавливает также условия, при которых результаты лабораторных исследований можно распространить на другие явления, подобные рассматриваемому. Ввиду этого теория подобия является теоретической базой эксперимента, но не только. Теория подобия является важным подспорьем теоретических исследований. Хотя методами теории подобия вид искомой функции не может быть определен, эта теория облегчает в ряде случаев анализ процесса и описание полученных результатов.
Для практического использования выводов теории подобия необходимо уметь приводить к безразмерному виду математические описания изучаемых процессов.
Имеется несколько методов, и один из них — метод масштабных преобразований.
независимые переменные: х, у.
зависимые переменные:
постоянные величины: 
Таким образом, искомые зависимые переменные 
В качестве масштабов удобно принять постоянные величины 









Помимо безразмерных величин 
Безразмерные соотношения параметров характеризующих процесс, имеющие у подобных явлений в сходственных точках численно одинаковые значения называются числами подобия.
1). У подобных явлений числа подобия численно одинаковы.
2). Интеграл дифференциальной функции (или системы уравнений) может быть представлен как функция чисел дифференциального уравнения.
3). Подобны те явления, условия однозначности которых подобны, и числа подобия, составленные из условия однозначности, численно одинаковы.
Условия однозначности: Явление, протекающее в геометрически подобных системах; для рассматривания явления можно составить дифференциальные уравнения; установлены существование и единственность решения уравнений при заданных граничных условиях; известны числовые значения коэффициентов и физических параметров.
Видео:Методы исследования технологических процессов. Теория подобия. Виды подобияСкачать

Реферат: Основы теории подобия (метод обобщенных переменных)
| Название: Основы теории подобия (метод обобщенных переменных) Раздел: Рефераты по экономико-математическому моделированию Тип: реферат Добавлен 03:53:33 03 июня 2011 Похожие работы Просмотров: 9858 Комментариев: 23 Оценило: 7 человек Средний балл: 4.1 Оценка: 4 Скачать | |||||||||||||||
| Критерий | Выражение критерия | Характеристика критериев | Единицы измерения входящих в критерии подобия величин |
| Кинематический (критерий Рейнольдса) | Rе=υl/ν= υlρ/μ | Характеризует меру соотношения сил инерции и сил трения | |
| Гравитационный (критерий Фруда) | Fr =υ 2 /gl | Характеризует меру соотношения сил инерции и сил тяжести | |
| Гидравлического сопротивления (критерий Эйлера) | Еu =∆p/ρ υ 2 | Характеризует меру соотношения сил гидростатического давления и сил инерции | |
| Гомохронности | Но =υ τ/l | Характеризует неустановившееся движение жидкости |
Таким образом, дифференциальное уравнение Навье — Стокса, описывающее движение вязкой жидкости, может быть представлено в виде критериального уравнения:
f (Rе, Но, Fr, Еu) = 0 (8)
Уравнение (8) является обобщенным критериальным уравнением гидродинамики. Все критерии уравнения (8), кроме критерия Ей, являются определяющими, так как они составлены из величин, входящих в условия однозначности. Критерий Эйлера, в который входит величина ∆р, являющаяся целью расчета, будет определяемым критерием.
Еu = f (Rе, Но, Fr) или
Еu = AНо с Rе т Fr п , (9)
где А,c,т,п- эмпирические показатели.
В ряде случаев уравнение (19) дополняют геометрическим симплексом l / d :
Еu = AНо с Rе т Fr п (l / d ) b , (10)
где b- эмпирический показатель.
При установившемся движении критерий Но исключается из критериального уравнения:
Еu = ARе т Fr п (l / d ) b . (11)
В случае, если скорость движения жидкости не определена, в расчеты вводят производные или модифицированные критерии подобия, составленные из основных критериев. В этих критериях подобия неизвестная величина υ заменяется другими величинами, которые сравнительно легко определяются экспериментально или аналитически.
Возьмем отношение критериев Rе и Fr:

Полученный безразмерный комплекс величин называется критерием Галилея. Если умножить этот критерий на отношение ( ρ 1 — ρ 2 )/ ρ 2 , то получается новый критерий подобия — критерий Архимеда

где ρ 1 , ρ 2 — плотности жидкости в разных точках, кг/м 3 .
📸 Видео
Подобие процессов конвективного теплообменаСкачать

Тепловое и массообменное подобиеСкачать

Лекция 1.4 Оcновы теории подобия. Критериальные параметры.Скачать

Термодинамика Л31. 2024. Конвективный тепломассообмен. Критерии подобия. Лучистый теплообменСкачать

Лекция по теплофизике. 26.04.2021Скачать

Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

1 Лекция МиОЭП 8 семестр 15.02.2021Скачать

Жмакин В.А. Лекция №4 «Научные исследования на физических моделях. Физическое моделирование»Скачать

Физическое моделирование Гидродинамическое подобиеСкачать

Моделирование химико-технологических процессов. Часть 3. Уровень: базовый.Скачать

Л2 - Конвективный теплообмен.Скачать

Единую Метафизику Целевых Потоков Целостного Движения (Электронных, Когнитивных) квантует ПервеансСкачать

Краткие пояснения к лекции от 10 сентябряСкачать

Основы конвективного теплообменаСкачать

Урок 138. Число Рейнольдса. Критерий Рейнольдса.Скачать

Деловое СкороМышление от Математики: Матрица 3х3 Пифагора, СКВ Кибальникова, Целевая ФункцияСкачать

Объяснение некоторых вопросов тестаСкачать

8 класс, 22 урок, Первый признак подобия треугольниковСкачать

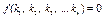
 (1)
(1)
 (2)
(2) (3)
(3) (4)
(4)