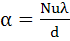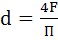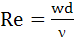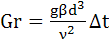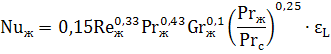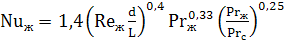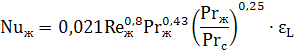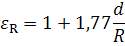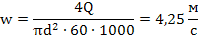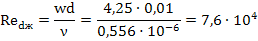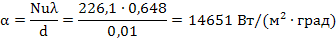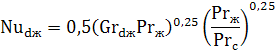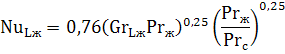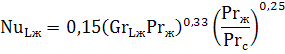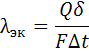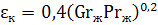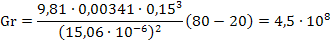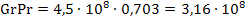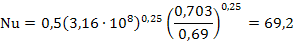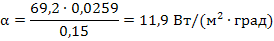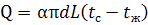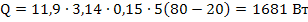Критериальные уравнения для горизонтальных труб омываемых жидкостями или газами

Основной задачей при исследованиях конвективного теплообмена является определение коэффициента теплоотдачи, который входит только в число Nu. Поэтому уравнения конвективного теплообмена в безразмерном виде решаются только относительно числа Nu. В работе [1] многочисленные эксперименты были обобщены в виде:

Значения коэффициента С и показателей степени т,п,р определяются опытным путем для конкретных случаев конвективного теплообмена. Обычно указываются определяющие температура и размер.

В работах [1, 2, 4] приведены критериальные уравнения для ламинарного и турбулентного режимов течения газов и жидкостей при различных условиях обтекания.

Рассмотрим теплоотдачу при движении потока внутри трубы.

Ламинарный режим течения наблюдается при Re 10 4 . Значения Re от Re_;/; до ю 4 соответствуют переходному режиму. Вследствие теплообмена плотность текущей среды может быть неоднородной по сечению и длине канала, и при определенных числах Ra в вынужденном потоке может возникнуть и развиваться свободная конвекция. Ламинарное течение в отсутствие свободной конвекции принято называть вязкостным, а течение, сопровождающееся свободной конвекцией, —вязкостно-гравитационным. Вязкостный режим тем более вероятен, чем больше вязкость жидкости и чем меньше диаметр трубы и температурный напор. В условиях теплообмена даже в отсутствие влияния свободной конвекции распределение скорости по сечению трубы может значительно отличаться от профиля скорости изотермического потока, если вязкость существенно зависит от температуры. У капельных жидкостей, например, с ростом температуры вязкость падает. В результате при нагревании потока скорость вблизи стенки больше, чем при охлаждении, и соответственно интенсивнее теплоотдача.

На начальном участке канала профили скорости и температуры жидкости (газа) изменяются от состояния во входном сечении до полностью развитой по сечению потока формы. Эти участки называются гидродинамическим и тепловым начальным участком, на которых формируются соответственно гидродинамический и тепловой пограничные слои. По мере развития пограничных слоев теплоотдача падает, число Nu уменьшается, асимптотически приближаясь к постоянному значению Nu°°. Это значение называется предельным и характеризует интенсивность теплоотдачи полностью стабилизированного потока. В длинных трубах (/ »/_ги / »1_Т‘, 1_Г,1_Т — длина начальных участков соответственно гидродинамический и тепловой стабилизации) среднюю теплоотдачу можно считать равной предельной: Nu^Nu^.

Значения 1_Г и 1_Т определяются следующим образом:

l_r = к Re J и I = к (Re • Рг_/Л)J , (2.83) где к_г и к_т — коэффициенты, зависящие от формы канала; d_9Ke — эквивалентный диаметр сечения канала (отношение площади к периметру канала).

Для вязкостного режима движения (Ra_nc 5 ) при условиях | | > 20 И ^ ж /.. — 0,00067 4-14,3 среднее ПО длине трубы

число Nu при постоянной температуре стенки может быть, например, определено по формуле [4]:

где / и d_e— длина и внутренний диаметр трубы; Є, — поправка на участок гидродинамической стабилизации.

При незначительном изменении температуры жидкости по длине за определяющую температуру принимается t_nc = 0,5 (t_c — ї_ж), и соответственно в Gr вводится А/ = (t_c — ї_ж ). В противном случае определяющей температурой для Nu,Pe,/H_)K является t = t_c — 0,5А7_Л, где среднелогарифмический напор находится по формуле:

где t_c— средняя температура стенки; 1_ЖР_Ж — соответственно температура набегающего потока или среднемассовая температура на входе в трубу и температура на выходе из трубы.

Для Gr и Рг физические свойства жидкости выбираются по / = 0,5(г_ж-/)и Дг = (/,.-г).

Для вязкостно-гравитационного режима движения (Ra_nc

8 • 10 5 -г-13 • 10 6 ) при условиях ^Pe^^j = 204-120, Re_x =2-ї-10 в горизонтальных трубах число Nu_n._c. может быть определено по формуле [4]:

В вертикальных трубах при совпадении направлений вынужденной и свободной конвекции у стенки средняя теплоотдача определяется по формуле:

ТЕПЛООТДАЧА ПРИ ВЫНУЖДЕННОМ ТЕЧЕНИИ ЖИДКОСТИ В ГОРИЗОНТАЛЬНЫХ ТРУБАХ

Режим течения жидкости в трубах может быть ламинарным или турбулентным. О режиме течения жидкости судят по величине числа Рейнольдса Re = Ud/v, где d — внутренний диаметр трубы ий — средняя скорость движения жидкости.

Если Re Re_Kp2 * 10 4 . Течение жидкости в диапазоне чисел Re = 2 10 3 -10 4 называется переходным.

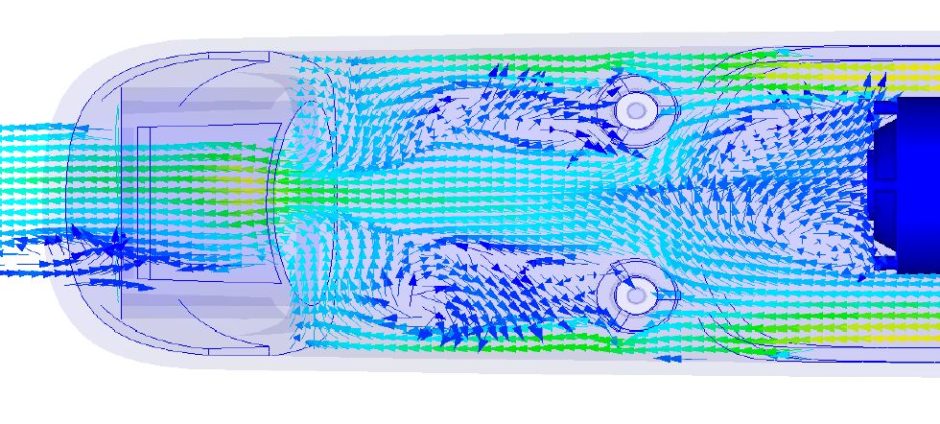
Распределение скоростей при движении жидкости в трубе

Будем считать, что распределение скоростей движения на входе в трубу однородное (рис. 15.14). При дальнейшем движении жидкости у стенок трубы формируется гидродинамический пограничный слой, толщина которого постепенно возрастает, причем в длинных трубах пограничные слои сливаются на оси трубы и в трубе устанавливается неизменное распределение скоростей, характерное для данного режима течения.

Расстояние, на котором устанавливается постоянное распределение скоростей, называется начальным участком 1_Н (рис. 15.14) (см. часть II «Основы гидравлики»). Аналогично гидродинамическому начальному участку существует и начальный участок тепловой стабилизации 1_и_ _т. На длине этого участка центральное ядро жидкости еще не участвует в теплообмене и имеет температуру, равную температуре жидкости на входе в трубу. За участком тепловой стабилизации 1_Н т в процессе теплообмена участвует весь поток жидкости. При ламинарном течении жидкости величина 1_Н т достаточно велика (сотни диаметров трубы). При турбулентном течении жидкости 1_Н т * 50d. Величина коэффициента теплоотдачи максимальна на входе в трубу, а затем убывает и после прохождения жидкостью 1_Н т стабилизируется.

ТЕПЛООТДАЧА ПРИ ЛАМИНАРНОМ РЕЖИМЕ

При ламинарном течении жидкости могут иметь место вязкостный и гравитационно-вязкостный режимы. Вязкостный режим наблюдается при преобладании сил вязкости жидкости над подъемными силами (течение вязких жидкостей при незначительном влиянии естествен hi и hi и hi ш и til и ж и til и ж uni ill и hi и ill и ill ill и iti и ill и iti ill и ill ti ill и min и ж и til inn hi и hi и ж и hi iti и hi и iti и hi hi ti hi и hi inn и min и ж ши и ж inn hi и ж и hi и ж и hi iti и hi и iti и hi hi и и ной конвекции). Влияние естественной (свободной) конвекции заметно при Ra = GrPr > 810 5 .

Критериальное уравнение для расчета среднего (по длине трубы I) коэффициента теплоотдачи при вязкостном режиме течения жидкости в случае, когда длина трубы больше 1_Н т, имеет вид

В этом уравнении Nu = ad/X; a = q_c /(t_c -t); q_c — средняя по внутренней поверхности трубы плотность теплового потока. Физические свойства жидкости находятся по определяющей температуре t = t_c±0,5At_j4, где ДА, —среднелогарифмический температурный напор. Поправка на начальный гидродинамический участок е₍ существенна только для относительно коротких труб. При Red > 10 е,= 1,0.

При течении жидкости в вертикальной трубе (снизу вверх при охлаждении и сверху вниз при нагревании) средний коэффициент теплоотдачи может быть найден из уравнения подобия:

где п = 0,11 при нагревании и п = 0,2 5 при охлаждении жидкости; коэффициент теплоотдачи отнесен к среднеарифметическому температурному напору At_& =t_c-t_x, физические параметры жидкости выбираются при температуре — 0,5(i_BX +?_вых).

Уравнение (15.43) можно использовать в следующем диапазоне чисел подобия: Re = 250Ю 4 ; Ra^, = (1,5-12)10®; Рг_р= 2-10. Индекс р означает, что теплофизические параметры жидкости выбираются по расчетной температуре t_p=0,5(t_c +Т_Ж).

При гравитационно-вязкостном режиме течения (Ra = = GrPr > 810 5 ) для приближенного расчета коэффициента теплоотдачи может использоваться полученное М. А. Михеевым уравнение

Значения ё₍ при ламинарном режиме течения жидкости

Критериальные уравнения теплообмена: расчет теплоотдачи в трубах и каналах

Теплоотдача при вынужденном течении жидкости в трубах и каналах

Теплоотдача в трубах и каналах может происходить при вынужденном или свободном характере конвекционных потоков (возможны также их сочетания в случае существенного влияния гравитационных сил).

При вынужденном течении (вынужденная конвекция) жидкость нагнетается или отводится под действием сил внешнего давления, например, ветра, насоса или вентилятора.

Свободное течение жидкости происходит под действием подъемных (гравитационных) сил за счет изменения ее плотности из-за разницы температуры – слой жидкости с меньшей плотностью стремиться занять верхнее положение относительно холодного слоя (свободная или естественная конвекция).

Интенсивность теплоотдачи, как при вынужденной, так и при свободной конвекции характеризуется коэффициентом теплоотдачи α, имеющим размерность Вт/(м 2 ·град), который определяется по формуле:

Nu – число Нуссельта; λ – коэффициент теплопроводности жидкости при средней температуре, Вт/(м·град);

d – эквивалентный диаметр, равный

F – площадь сечения канала, м 2 ; П – периметр канала, м.

Для трубы круглого сечения, эквивалентный диаметр равен внутреннему диаметру трубы.

В целом, расчет коэффициента теплоотдачи сводится к определению числа Нуссельта, значение которого задается соответствующими критериальными уравнениями конвективного теплообмена, зависящими от режима течения жидкости и формы канала.

Течение жидкости в трубах определяется значением числа Рейнольдса Re и в зависимости от его величины может быть ламинарным, переходным или турбулентным.

• Ламинарный режим течения жидкости характеризуется величиной числа Re до 2300.
• При значении числа Re от 2300 до 10000 режим течения в трубах является переходным.
• Турбулентный режим течения в трубах наблюдается при числах Re более 10000.

Число (критерий) Рейнольдса представляет собой безразмерный комплекс, связывающий скоростные и вязкостные характеристики жидкости с определяющим размером канала (для трубы – это ее диаметр).

Число Re определяется по формуле:

w – скорость течения жидкости, м/с; d – эквивалентный диаметр канала, м; ν — кинематическая вязкость жидкости при средней температуре, м 2 /с.

Теплоотдача в трубах и каналах существенно зависит от режима течения жидкости. При ламинарном режиме интенсивность теплоотдачи значительно меньше, чем при развитом турбулентном.

Теплоотдача при ламинарном течении в трубах и каналах

Ламинарный режим течения жидкости обычно характеризуется низкой скоростью потока. При этом в некоторых случаях влиянием конвекции, обусловленной действием гравитационных сил, пренебрегать нельзя.

Для выбора правильного критериального уравнения теплообмена и оценки влияния естественной конвекции на интенсивность теплопередачи при ламинарном режиме служит критерий Грасгофа Gr.

g – ускорение свободного падения, м/с 2 ;

β – температурный коэффициент объемного расширения, град -1 ;

d – эквивалентный диаметр канала, м;

ν — кинематическая вязкость жидкости при средней температуре, м 2 /с;

Δt – средняя разность температур жидкости и стенки, °С.

Теплоотдача при ламинарном течении в трубах и каналах с учетом естественной конвекции. Если величина комплекса GrPr превышает 8·10 5 , то расчет коэффициента теплоотдачи необходимо проводить с учетом влияния естественной конвекции в потоке жидкости по следующему критериальному уравнению:

Индекс «ж» означает, что свойства среды, входящие в критерии подобия Re, Pr и Gr берутся при средней температуре жидкости.

Число Прандтля с индексом «с» Pr_с берется для жидкости при температуре стенки.

ε_L – коэффициент, учитывающий изменение теплоотдачи по длине трубы или канала. Его можно определить с помощью таблицы:

Значения коэффициента ε_L при ламинарном режиме

L/d	1	2	5	10	15	20	30	40	50
εL	1,9	1,7	1,44	1,28	1,18	1,13	1,05	1,02	1

Теплоотдача при ламинарном течении в трубах и каналах без учета естественной конвекции. При значении GrPr 5 , влияние естественной конвекции на теплоотдачу жидкости пренебрежительно мало, и расчет коэффициента теплоотдачи можно проводить по следующему критериальному уравнению:

d – эквивалентный диаметр канала, м;

L – длина трубы (канала), м.

Представленные критериальные уравнения теплообмена при ламинарном режиме позволяют определить среднее значение числа Нуссельта, по величине которого можно рассчитать средний коэффициент теплоотдачи:

λ – коэффициент теплопроводности жидкости при средней температуре, Вт/(м·град);

d – эквивалентный диаметр, м.

Теплоотдача в трубах и каналах при турбулентном режиме

Теплоотдача в трубах и каналах при турбулентном режиме осуществляется путем передачи тепла при интенсивном перемешивании слоев жидкости. Критериальное уравнение теплообмена для расчета средней теплоотдачи в трубах и каналах в этом случае имеет вид:

Критерии подобия Re и Pr берутся при средней температуре жидкости. Число Прандтля с индексом «с» Pr_с берется при температуре стенки.

Представленное критериальное уравнение применяется в диапазоне чисел Re от 1·10 4 до 5·10 6 и Pr от 0,6 до 2500.

ε_L – коэффициент, учитывающий изменение среднего коэффициента теплоотдачи по длине трубы или канала при турбулентном режиме течения. Значения ε_L приведены в следующей таблице при различных числах Рейнольдса и отношениях длины канала к его эквивалентному диаметру:

Значения коэффициента ε_L при турбулентном режиме

Reж	L/d
	1	2	5	10	15	20	30	40	50
1·10 4	1,65	1,5	1,34	1,23	1,17	1,13	1,07	1,03	1
2·10 4	1,51	1,4	1,27	1,18	1,13	1,1	1,05	1,02	1
5·10 4	1,34	1,27	1,18	1,13	1,1	1,08	1,04	1,02	1
1·10 5	1,28	1,22	1,15	1,1	1,08	1,06	1,03	1,02	1
1·10 6	1,14	1,11	1,08	1,05	1,04	1,03	1,02	1,01	1

Расчет теплоотдачи в изогнутых трубах и каналах проводится по тому же критериальному уравнению с добавлением множителя — поправки на действие центробежных сил, которая определяется по формуле:

R — радиус изгиба трубы или канала, м; d – эквивалентный диаметр трубы или канала, м.

Теплоотдача в изогнутых трубах проходит более интенсивно, чем в прямых, за счет большего вихреобразования и лучшего перемешивания жидкости.

Расчет теплоотдачи при вынужденной конвекции

Пример расчета. Рассчитаем средний коэффициент теплоотдачи воды, текущей по трубопроводу длиной 1 м, диаметром d=0,01 м с расходом Q=20 л/мин. Средняя температура воды t_ж=50°С, температура стенки трубы t_с=10°С.

1. Определим физические свойства воды при температуре 50°С:

• Теплопроводность воды λ_ж= 0,648 Вт/(м·град);
• Плотность воды ρ_ж=988 кг/м 3 ;
• Кинематическая вязкость воды ν_ж=0,556·10 -6 , м 2 /с;
• Число Прандтля при температуре жидкости Pr_ж=3,54;
• Число Прандтля при температуре стенки Pr_с=9,52.

2. Рассчитаем среднюю скорость течения воды w по трубе:

3. Определим число Рейнольдса Re:

4. Поскольку число Рейнольдса имеет значение больше 1·10 4 , то режим течения является турбулентным и расчет теплоотдачи необходимо проводить по следующему критериальному уравнению:

Определим коэффициент ε_L по соотношению L/d=1/0,01=100. Поскольку L/d>50, то коэффициент ε_L=1_.

Выполним расчет числа Нуссельта по приведенному критериальному уравнению:

5. Рассчитаем средний коэффициент теплоотдачи от воды к стенке трубы по формуле:

Таким образом, средний коэффициент теплоотдачи от воды к стенке трубы составляет 14,65 кВт/(м 2 ·град).

Теплоотдача при свободной конвекции в трубах и каналах

Теплообмен при свободном движении жидкости (или газа) происходит вследствие разности плотностей нагретых и холодных ее слоев. Интенсивность теплоотдачи жидкости в трубах и каналах при свободной конвекции существенно зависит от их положения в пространстве относительно силы тяжести.

Теплоотдача при свободной конвекции имеет различный характер в случаях свободного течения в неограниченном пространстве и теплообмена в ограниченном объеме (в узкой трубе или канале).

Свободная конвекция в неограниченном пространстве

Конвекция в неограниченном пространстве протекает, например при охлаждении трубопровода центрального отопления, расположенного на улице в безветренную погоду, вблизи от которого отсутствуют препятствия для движения воздушных потоков.

Горизонтальный канал или труба. Интенсивность теплоотдачи при свободной конвекции зависит от величины комплекса GrPr. При значении GrPr от 10 3 до 10 9 критериальное уравнение, описывающее среднюю теплоотдачу от поверхности горизонтальных труб и каналов, имеет вид:

В качестве определяющего размера принимается наружный диаметр d канала или трубы.

Вертикальный канал (труба, пластина). Для вертикальных труб и каналов при значении GrPr от 10 3 до 10 9 критериальное уравнение, описывающее среднюю теплоотдачу, имеет вид:

При GrPr>10 9 :

Примечание: В приведенных критериальных уравнениях теплообмена свойства жидкости, входящие в числа Gr и Pr, определяются при температуре окружающей среды. Число Прандтля с индексом «с» Pr_с берется для жидкости при температуре стенки. В качестве определяющего размера принимается длина L (высота) вертикально стоящей трубы или канала.

Свободная конвекция в ограниченном объеме

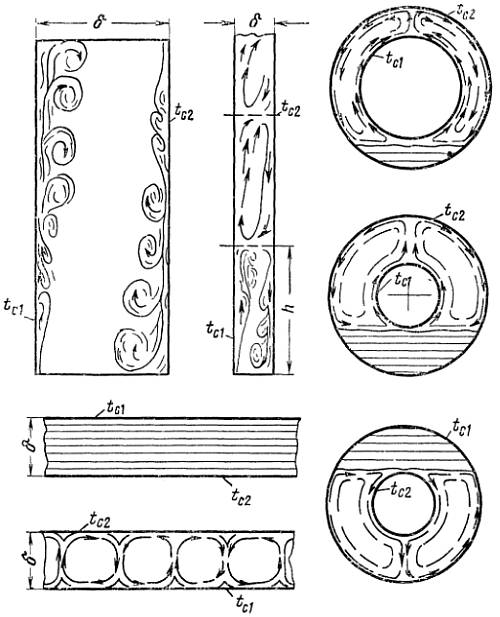
Теплообмен жидкости в ограниченном объеме при свободной конвекции характеризуется совместным протеканием процессов нагрева и охлаждения соседних слоев жидкости (или газа). Эти процессы сопровождаются сложным течением нисходящих и восходящих потоков, зависящих от рода жидкости, разницы температуры, формы канала и его геометрических размеров.

Для упрощения расчета таких сложных процессов конвективного теплообмена принято рассматривать их, как явление теплопроводности в щели толщиной δ с учетом понятия эквивалентного коэффициента теплопроводности λ_эк.

Эквивалентный коэффициент теплопроводности определяется по формуле:

Q — количество переданного тепла, Вт; δ — толщина слоя жидкости (или газа), м; F — площадь теплоотдающей поверхности, м 2 ; Δt=t_c1-t_c2 — температурный напор между нагретой и холодной стенками, °С.

Отношение эквивалентного коэффициента теплопроводности λ_эк к величине теплопроводности окружающей жидкости при средней температуре называется коэффициентом конвекции ε_к, который определяется значением комплекса GrPr.

При малых значениях комплекса GrPr 3 6 :

При 10 6 10 :

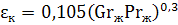
Примечание: Числа подобия Gr и Pr рассчитываются при средней температуре жидкости (или газа), равной t_ж=0,5(t_c1+t_c2). В качестве определяющего размера принимается δ — толщина слоя жидкости.

Расчет теплоотдачи при свободной конвекции

Пример расчета. Рассчитаем потери тепла естественной конвекцией от горизонтального трубопровода центрального отопления, находящегося на открытом воздухе. Диаметр трубопровода d=0,15 м, длина L=5 м, средняя температура наружной стенки t_с=80°С. Температура окружающего воздуха t_ж=20°С.

1. Определим физические свойства воздуха при температуре 20°С:

• Теплопроводность воздуха λ_ж= 0,0259 Вт/(м·град);
• Кинематическая вязкость воздуха ν_ж=15,06·10 -6 , м 2 /с;
• Число Прандтля при температуре жидкости Pr_ж=0,703;
• Число Прандтля при температуре стенки Pr_с=0,69;
• Коэффициент объемного расширения β_ж=1/(273+20)=0,00341 град -1 .

2. Вычислим число Грасгофа Gr по формуле:

3. Определим значение комплекса GrPr:

Этому значению комплекса соответствует следующее критериальное уравнение теплообмена при свободной конвекции в случае горизонтальной трубы:

4. Вычислим значение числа Нуссельта Nu:

5. Рассчитаем коэффициент теплоотдачи от трубы α по формуле:

6. Определим потери тепла с боковой поверхности трубопровода по формуле:

Подставляя численные значения, окончательно получаем потерю тепла:

Таким образом, только путем естественной (свободной) конвекции рассмотренный трубопровод отопления отдает воздуху 1681 Вт тепла.

📸 Видео