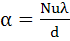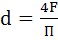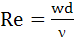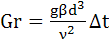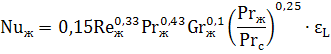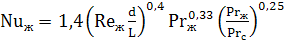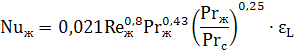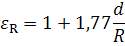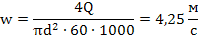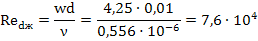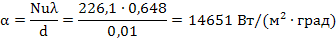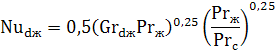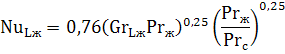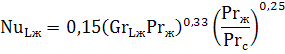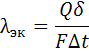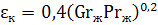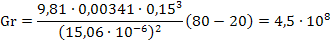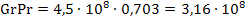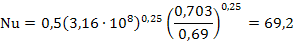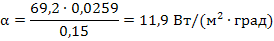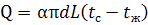Критериальное уравнение для теплоотдачи в условиях вынужденной конвекции

Критериальные уравнения теплообмена: расчет теплоотдачи в трубах и каналах

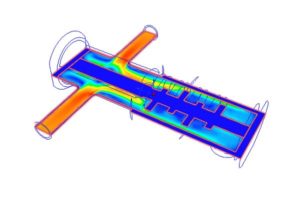
Теплоотдача при вынужденном течении жидкости в трубах и каналах

Теплоотдача в трубах и каналах может происходить при вынужденном или свободном характере конвекционных потоков (возможны также их сочетания в случае существенного влияния гравитационных сил).

При вынужденном течении (вынужденная конвекция) жидкость нагнетается или отводится под действием сил внешнего давления, например, ветра, насоса или вентилятора.

Свободное течение жидкости происходит под действием подъемных (гравитационных) сил за счет изменения ее плотности из-за разницы температуры – слой жидкости с меньшей плотностью стремиться занять верхнее положение относительно холодного слоя (свободная или естественная конвекция).

Интенсивность теплоотдачи, как при вынужденной, так и при свободной конвекции характеризуется коэффициентом теплоотдачи α, имеющим размерность Вт/(м 2 ·град), который определяется по формуле:

Nu – число Нуссельта; λ – коэффициент теплопроводности жидкости при средней температуре, Вт/(м·град);

d – эквивалентный диаметр, равный

F – площадь сечения канала, м 2 ; П – периметр канала, м.

Для трубы круглого сечения, эквивалентный диаметр равен внутреннему диаметру трубы.

В целом, расчет коэффициента теплоотдачи сводится к определению числа Нуссельта, значение которого задается соответствующими критериальными уравнениями конвективного теплообмена, зависящими от режима течения жидкости и формы канала.

Течение жидкости в трубах определяется значением числа Рейнольдса Re и в зависимости от его величины может быть ламинарным, переходным или турбулентным.

• Ламинарный режим течения жидкости характеризуется величиной числа Re до 2300.
• При значении числа Re от 2300 до 10000 режим течения в трубах является переходным.
• Турбулентный режим течения в трубах наблюдается при числах Re более 10000.

Число (критерий) Рейнольдса представляет собой безразмерный комплекс, связывающий скоростные и вязкостные характеристики жидкости с определяющим размером канала (для трубы – это ее диаметр).

Число Re определяется по формуле:

w – скорость течения жидкости, м/с; d – эквивалентный диаметр канала, м; ν — кинематическая вязкость жидкости при средней температуре, м 2 /с.

Теплоотдача в трубах и каналах существенно зависит от режима течения жидкости. При ламинарном режиме интенсивность теплоотдачи значительно меньше, чем при развитом турбулентном.

Теплоотдача при ламинарном течении в трубах и каналах

Ламинарный режим течения жидкости обычно характеризуется низкой скоростью потока. При этом в некоторых случаях влиянием конвекции, обусловленной действием гравитационных сил, пренебрегать нельзя.

Для выбора правильного критериального уравнения теплообмена и оценки влияния естественной конвекции на интенсивность теплопередачи при ламинарном режиме служит критерий Грасгофа Gr.

g – ускорение свободного падения, м/с 2 ;

β – температурный коэффициент объемного расширения, град -1 ;

d – эквивалентный диаметр канала, м;

ν — кинематическая вязкость жидкости при средней температуре, м 2 /с;

Δt – средняя разность температур жидкости и стенки, °С.

Теплоотдача при ламинарном течении в трубах и каналах с учетом естественной конвекции. Если величина комплекса GrPr превышает 8·10 5 , то расчет коэффициента теплоотдачи необходимо проводить с учетом влияния естественной конвекции в потоке жидкости по следующему критериальному уравнению:

Индекс «ж» означает, что свойства среды, входящие в критерии подобия Re, Pr и Gr берутся при средней температуре жидкости.

Число Прандтля с индексом «с» Pr_с берется для жидкости при температуре стенки.

ε_L – коэффициент, учитывающий изменение теплоотдачи по длине трубы или канала. Его можно определить с помощью таблицы:

Значения коэффициента ε_L при ламинарном режиме

L/d	1	2	5	10	15	20	30	40	50
εL	1,9	1,7	1,44	1,28	1,18	1,13	1,05	1,02	1

Теплоотдача при ламинарном течении в трубах и каналах без учета естественной конвекции. При значении GrPr 5 , влияние естественной конвекции на теплоотдачу жидкости пренебрежительно мало, и расчет коэффициента теплоотдачи можно проводить по следующему критериальному уравнению:

d – эквивалентный диаметр канала, м;

L – длина трубы (канала), м.

Представленные критериальные уравнения теплообмена при ламинарном режиме позволяют определить среднее значение числа Нуссельта, по величине которого можно рассчитать средний коэффициент теплоотдачи:

λ – коэффициент теплопроводности жидкости при средней температуре, Вт/(м·град);

d – эквивалентный диаметр, м.

Теплоотдача в трубах и каналах при турбулентном режиме

Теплоотдача в трубах и каналах при турбулентном режиме осуществляется путем передачи тепла при интенсивном перемешивании слоев жидкости. Критериальное уравнение теплообмена для расчета средней теплоотдачи в трубах и каналах в этом случае имеет вид:

Критерии подобия Re и Pr берутся при средней температуре жидкости. Число Прандтля с индексом «с» Pr_с берется при температуре стенки.

Представленное критериальное уравнение применяется в диапазоне чисел Re от 1·10 4 до 5·10 6 и Pr от 0,6 до 2500.

ε_L – коэффициент, учитывающий изменение среднего коэффициента теплоотдачи по длине трубы или канала при турбулентном режиме течения. Значения ε_L приведены в следующей таблице при различных числах Рейнольдса и отношениях длины канала к его эквивалентному диаметру:

Значения коэффициента ε_L при турбулентном режиме

Reж	L/d
	1	2	5	10	15	20	30	40	50
1·10 4	1,65	1,5	1,34	1,23	1,17	1,13	1,07	1,03	1
2·10 4	1,51	1,4	1,27	1,18	1,13	1,1	1,05	1,02	1
5·10 4	1,34	1,27	1,18	1,13	1,1	1,08	1,04	1,02	1
1·10 5	1,28	1,22	1,15	1,1	1,08	1,06	1,03	1,02	1
1·10 6	1,14	1,11	1,08	1,05	1,04	1,03	1,02	1,01	1

Расчет теплоотдачи в изогнутых трубах и каналах проводится по тому же критериальному уравнению с добавлением множителя — поправки на действие центробежных сил, которая определяется по формуле:

R — радиус изгиба трубы или канала, м; d – эквивалентный диаметр трубы или канала, м.

Теплоотдача в изогнутых трубах проходит более интенсивно, чем в прямых, за счет большего вихреобразования и лучшего перемешивания жидкости.

Расчет теплоотдачи при вынужденной конвекции

Пример расчета. Рассчитаем средний коэффициент теплоотдачи воды, текущей по трубопроводу длиной 1 м, диаметром d=0,01 м с расходом Q=20 л/мин. Средняя температура воды t_ж=50°С, температура стенки трубы t_с=10°С.

1. Определим физические свойства воды при температуре 50°С:

• Теплопроводность воды λ_ж= 0,648 Вт/(м·град);
• Плотность воды ρ_ж=988 кг/м 3 ;
• Кинематическая вязкость воды ν_ж=0,556·10 -6 , м 2 /с;
• Число Прандтля при температуре жидкости Pr_ж=3,54;
• Число Прандтля при температуре стенки Pr_с=9,52.

2. Рассчитаем среднюю скорость течения воды w по трубе:

3. Определим число Рейнольдса Re:

4. Поскольку число Рейнольдса имеет значение больше 1·10 4 , то режим течения является турбулентным и расчет теплоотдачи необходимо проводить по следующему критериальному уравнению:

Определим коэффициент ε_L по соотношению L/d=1/0,01=100. Поскольку L/d>50, то коэффициент ε_L=1_.

Выполним расчет числа Нуссельта по приведенному критериальному уравнению:

5. Рассчитаем средний коэффициент теплоотдачи от воды к стенке трубы по формуле:

Таким образом, средний коэффициент теплоотдачи от воды к стенке трубы составляет 14,65 кВт/(м 2 ·град).

Теплоотдача при свободной конвекции в трубах и каналах

Теплообмен при свободном движении жидкости (или газа) происходит вследствие разности плотностей нагретых и холодных ее слоев. Интенсивность теплоотдачи жидкости в трубах и каналах при свободной конвекции существенно зависит от их положения в пространстве относительно силы тяжести.

Теплоотдача при свободной конвекции имеет различный характер в случаях свободного течения в неограниченном пространстве и теплообмена в ограниченном объеме (в узкой трубе или канале).

Свободная конвекция в неограниченном пространстве

Конвекция в неограниченном пространстве протекает, например при охлаждении трубопровода центрального отопления, расположенного на улице в безветренную погоду, вблизи от которого отсутствуют препятствия для движения воздушных потоков.

Горизонтальный канал или труба. Интенсивность теплоотдачи при свободной конвекции зависит от величины комплекса GrPr. При значении GrPr от 10 3 до 10 9 критериальное уравнение, описывающее среднюю теплоотдачу от поверхности горизонтальных труб и каналов, имеет вид:

В качестве определяющего размера принимается наружный диаметр d канала или трубы.

Вертикальный канал (труба, пластина). Для вертикальных труб и каналов при значении GrPr от 10 3 до 10 9 критериальное уравнение, описывающее среднюю теплоотдачу, имеет вид:

При GrPr>10 9 :

Примечание: В приведенных критериальных уравнениях теплообмена свойства жидкости, входящие в числа Gr и Pr, определяются при температуре окружающей среды. Число Прандтля с индексом «с» Pr_с берется для жидкости при температуре стенки. В качестве определяющего размера принимается длина L (высота) вертикально стоящей трубы или канала.

Свободная конвекция в ограниченном объеме

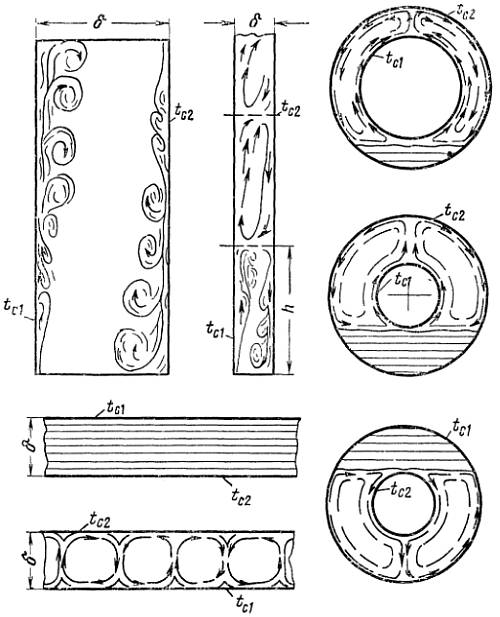
Теплообмен жидкости в ограниченном объеме при свободной конвекции характеризуется совместным протеканием процессов нагрева и охлаждения соседних слоев жидкости (или газа). Эти процессы сопровождаются сложным течением нисходящих и восходящих потоков, зависящих от рода жидкости, разницы температуры, формы канала и его геометрических размеров.

Для упрощения расчета таких сложных процессов конвективного теплообмена принято рассматривать их, как явление теплопроводности в щели толщиной δ с учетом понятия эквивалентного коэффициента теплопроводности λ_эк.

Эквивалентный коэффициент теплопроводности определяется по формуле:

Q — количество переданного тепла, Вт; δ — толщина слоя жидкости (или газа), м; F — площадь теплоотдающей поверхности, м 2 ; Δt=t_c1-t_c2 — температурный напор между нагретой и холодной стенками, °С.

Отношение эквивалентного коэффициента теплопроводности λ_эк к величине теплопроводности окружающей жидкости при средней температуре называется коэффициентом конвекции ε_к, который определяется значением комплекса GrPr.

При малых значениях комплекса GrPr 3 6 :

При 10 6 10 :

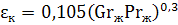
Примечание: Числа подобия Gr и Pr рассчитываются при средней температуре жидкости (или газа), равной t_ж=0,5(t_c1+t_c2). В качестве определяющего размера принимается δ — толщина слоя жидкости.

Расчет теплоотдачи при свободной конвекции

Пример расчета. Рассчитаем потери тепла естественной конвекцией от горизонтального трубопровода центрального отопления, находящегося на открытом воздухе. Диаметр трубопровода d=0,15 м, длина L=5 м, средняя температура наружной стенки t_с=80°С. Температура окружающего воздуха t_ж=20°С.

1. Определим физические свойства воздуха при температуре 20°С:

• Теплопроводность воздуха λ_ж= 0,0259 Вт/(м·град);
• Кинематическая вязкость воздуха ν_ж=15,06·10 -6 , м 2 /с;
• Число Прандтля при температуре жидкости Pr_ж=0,703;
• Число Прандтля при температуре стенки Pr_с=0,69;
• Коэффициент объемного расширения β_ж=1/(273+20)=0,00341 град -1 .

2. Вычислим число Грасгофа Gr по формуле:

3. Определим значение комплекса GrPr:

Этому значению комплекса соответствует следующее критериальное уравнение теплообмена при свободной конвекции в случае горизонтальной трубы:

4. Вычислим значение числа Нуссельта Nu:

5. Рассчитаем коэффициент теплоотдачи от трубы α по формуле:

6. Определим потери тепла с боковой поверхности трубопровода по формуле:

Подставляя численные значения, окончательно получаем потерю тепла:

Таким образом, только путем естественной (свободной) конвекции рассмотренный трубопровод отопления отдает воздуху 1681 Вт тепла.

Критериальные уравнения

Применяя общие законы физики, можно составить дифферен­циальные уравнения для конвективного теплообмена, учитываю­щие как тепловые, так и гидродинамические явления в любом процессе.

Система дифференциальных уравнений состоит из 6 уравнений: энергии (или теплопроводности), теплообмена, движения (3 уравнения) и уравнение сплош­ности.

В результате анализа этих уравнений получены критерии подобия и критериальные уравнения, которые используются при исследовании конвективного теплообмена.

Критериальным уравнением называют зависимость между каким-либо определяемым критерием подобия и другими определяющими критериями подобия.

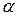
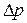
При расчете тепловых аппаратов искомыми величинами являют­ся коэффициент теплоотдачи и гидравлическое сопротивление . Конвективный теплообмен характеризуется пятью критериями подобия – Nu, Eu, Pr, Gr и Re.

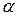
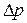
Критерий Нуссельта (Nu) содержит искомый коэффициент тепло­отдачи , а критерий Эйлера (Eu) – искомую величину , характеризую­щую гидравлическое сопротивление при движении жидкости. По­этому критерии Nu и Eu являются определяемыми критериями подобия, а критерии Прандтля (Pr), Грасгофа (Gr) и Рейнольдса (Re) – определяющими.

При конвективном теплообмене критериальные уравнения могут быть представлены в следующем виде:

(4.6)

(4.7)

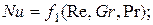
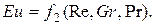
Зависимость между критериями в основном определяется опыт­ным путем.

В случае вынужденного движения жидкости и при развитом турбулентном режиме свободная конвекция в сравнении с вынужден­ной очень мала, поэтому критериальное уравнение теплоотдачи упрощается:

(4.8)

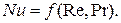
Для некоторых газов величина критерия Прандтля в процессе конвективного теплообмена почти не изменяется с температурой, поэтому критериальное уравнение принимает более простой вид:

(4.9)

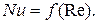
При свободном движении жидкости, когда вынужденная конвек­ция отсутствует, вместо критерия Рейнольдса в критериальное урав­нение теплоотдачи необходимо ввести критерий Грасгофа. При этом получается зависимость:

(4.10)

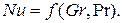
При исследовании теплообмена капельных жидкостей и газов со стенкой оказывается, что теплоотдача будет различной в усло­виях нагревания и охлаждения. Это явление связано с изменением физических параметров жидкости в пограничном слое. Для полу­чения критериальных уравнений, одинаково справедливых как для нагревания, так и для охлаждения, вводят дополнительно отно­шения:

, , . (4.11)

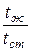
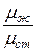
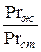
Первое соотношение обычно применяют при расчете теплоотдачи газов, остальные два – при расчете теплоотдачи капельных жид­костей.

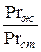
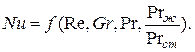
Академик М.А. Михеев рекомендует учитывать направление те­плового потока отношением . Тогда общее критериальное уравнение для конвективного теплообмена принимает следующий вид:

(4.12)

В такой же форме можно представить все уравнения для част­ных случаев. Количественная связь между критериями подобия и является предметом экспериментальных исследований.

Вопросы для самоконтроля к разделу 4

1. Что называется конвективным теплообменом?

2. Какие различают виды конвекции?

3. Гидродинамический и тепловой пограничные слои и их фи­зический смысл.

4. Какие встречаются виды движения жидкости и их различие?

5. Критерий Рейнольдса и его обозначение.

6. Какова размерность критерия Рейнольдса?

7. Критическое значение критерия Рейнольдса.

8. Каков механизм передачи теплоты при ламинарном и турбу­лентном движении

9. Дать определение динамической и кинематической вязкости.

10. Какие факторы влияют на конвективный теплообмен?

11. Определение коэффициента теплоотдачи.

12. Функцией каких величин является коэффициент тепло­отдачи?

13. Что называется условиями однозначности?

14. Почему для определения коэффициента теплоотдачи приме­няют теорию

15. Какие условия лежат в основе теории подобия?

16. От каких величин зависит коэффициент теплоотдачи?

17. Какие критерии подобия получают из дифференциальных уравнений

18. Какое уравнение называется критериальным?

19. Какими критериями подобия характеризуется конвективный теплообмен

Конвективный теплообмен

Конвективным теплообменом, или теплоотдачей, называется процесс переноса теплоты между поверхностью твердого тела и жидкой средой. При этом перенос теплоты осуществляется одновременным действием теплопроводности и конвекции.

Различают два вида конвекции: естественную (свободную) и вынужденную. При естественной конвекции движущая сила обусловлена разностью плотностей жидкости, вызванной ее контактом с поверхностью, имеющей другую температуру, вследствие чего возникают подъемные (архимедовы) силы. Типичными примерами такой конвекции являются теплоотдача от стен или крыши здания в безветренный день, конвекция в сосуде с жидкостью, в которую погружена нагревательная спираль, или теплоотдача от солнечного коллектора в безветренную погоду.

Вынужденная конвекция происходит в условиях, когда под действием внешней движущей силы жидкость обтекает поверхность, имеющую более высокую или более низкую температуру, чем сама жидкость. Поскольку скорость жидкости при вынужденной конвекции больше, чем при свободной, то в этом случае может быть передано больше теплоты при заданном перепаде температур. Это возрастание теплового потока компенсируется работой, затрачиваемой для приведения жидкости в движение. Но независимо от того, является ли конвекция свободной или вынужденной, мощность теплового потока 0 можно выразить с помощью закона Ньютона — Рихмана

где а_к — коэффициент конвективного теплообмена, Вт/(м 2 • °С); /?» — площадь поверхности, омываемой жидкостью, м 2 ; /_с — температура поверхности, °С; /_ж — температура жидкости, °С.

Коэффициент теплоотдачи можно определить как мощность теплового потока, переданного в единицу времени через единицу поверхности при разности температур между поверхностью и жидкостью в 1 °С.

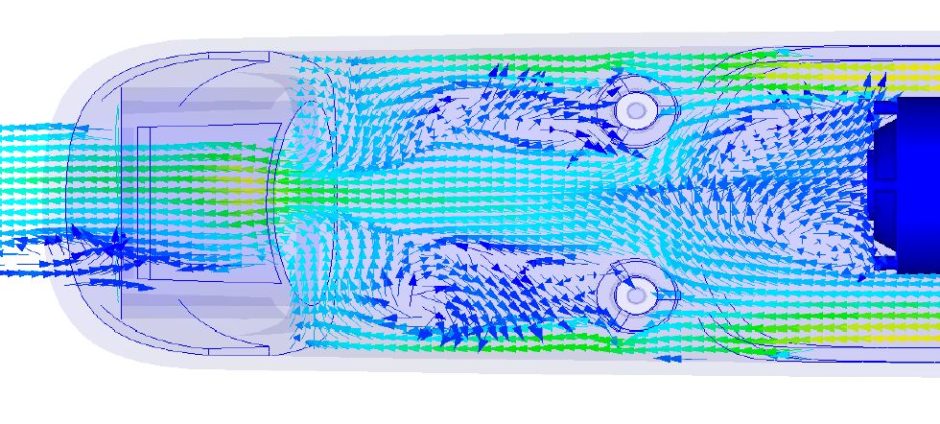
Физические процессы, объясняющие особенности конвективного теплообмена, показаны на рис. 1.7.

Нагретая плоская пластина охлаждается обтекающим ее потоком жидкости (воздуха). Профили скорости и температуры характеризуют пограничный слой, в пределах которого скорость движения жидкости изменяется от и_ж на границе слоя до V = 0 на поверхности пластины. В пограничном слое из-за действия сил

Рис. 1. 7. Профили скорости и температур при вынужденной конвекции около нагретой пластины

вязкости скорость и(у) уменьшается по направлению к стенке. Поскольку скорость слоя жидкости, примыкающего к стенке, равна нулю, плотность теплового потока от стенки к слою жидкости определяется переносом теплоты теплопроводностью. По мере удаления от стенки на границе пограничного слоя скорость увеличивается и становится равной скорости набегающего потока.

Коэффициент конвективной теплоотдачи зависит от плотности, вязкости и скорости жидкости, от ее теплофизических свойств (коэффициента теплопроводности и удельной теплоемкости), а также от размеров, формы тела, температуры поверхности и жидкости и других факторов.

Значения коэффициентов теплоотдачи можно определить из теоретического рассмотрения процесса конвективного теплообмена. Однако теоретические решения возможны лишь для систем достаточно простой геометрии. В инженерной практике коэффициенты теплоотдачи в реальных системах вычисляют по эмпирическим формулам, полученным путем совместного использования теории подобия и экспериментальных данных [1].

Получение эмпирических зависимостей основывается на рассмотрении геометрических и физических особенностей систем, в которых протекают подобные процессы, и их математическом описании.

На основании теорем подобия, без интегрирования дифференциальных уравнений, получаются критерии подобия, а на основании использования опытных данных устанавливаются критериальные зависимости, которые справедливы для всех подобных между собой процессов.

Уравнение подобия, или критериальное уравнение, для процессов конвективного теплообмена при вынужденном движении теплоносителя имеет вид

В процессах конвективного теплообмена в качестве определяемого критерия выступает критерии Нуссельта, характеризующий интенсивность процесса конвективного теплообмена:

где /— характерный геометрический размер, м; А. — коэффициент теплопроводности теплоносителя, Вт/(м • °С).

Коэффициент конвективного теплообмена рассчитывается кака_к = Ми-А.//.

Критерий Рейнольдса определяет гидромеханическое подобие течений теплоносителей:

где и₀ — характерная, обычно средняя скорость жидкости или газа в начальном сечении системы, м/с; / — характерный геометрический размер системы (например, диаметр канала, длина пластины и т.д.), м; V— коэффииент кинематической вязкости, м 2 /с.

Критерий Прандтля является теплофизической характеристикой теплоносителя. Он составлен лишь из физических параметров и его численные значения приводятся в таблицах:

При равенстве критериев Ле условие одинаковости критериев Рг обеспечивает тепловое подобие, т.е. подобие полей температурных напоров и тепловых потоков во всем объеме рассматриваемых систем.

Из уравнения (1.22) следует, что безразмерный коэффициент теплоотдачи, или число Нуссельта, зависит от чисел Рейнольдса и Прандтля. Удобной и сравнительно простой зависимостью для обобщения экспериментальных данных является уравнение, записанное в виде

где С, т, п — константы, которые необходимо определить экспериментальным путем.

В результате обобщения опытных данных по изучению конвективного теплообмена при продольном обтекании пластины различными жидкостями получены следующие критериальные уравнения.

При ламинарном режиме течения жидкости в пограничном слое локальный коэффициент теплоотдачи определяется из соотношения [1]

Для определения среднего коэффициента теплоотдачи из (1.27) можно получить зависимость

При турбулентном режиме течения в пограничном слое локальный коэффициент теплоотдачи определяется из соотношения

Для определения среднего коэффициента теплоотдачи из (1.29) получаем зависимость

Индексы «ж» и «с» указывают на то, что физические свойства теплоносителя относятся к и /. соответственно. Множитель (Рг_ж/Рг_с) , входящий в эти формулы, представляет собой поправку, учитывающую влияние изменения физических параметров теплоносителя с изменением температуры на теплоотдачу. Можно сказать, что этот множитель характеризует зависимость теплоотдачи от направления и величины теплового потока.

Расчетные формулы (1.27)—(1.30) для газов можно упростить.

Для воздуха Рг = 0,71 и расчетные формулы для средней теплоотдачи принимают вид:

— при ламинарном режиме течения в пограничном слое

— при турбулентном режиме течения в пограничном слое

В процессах естественной конвекции определяющими критериями подобия будут критерий Грасгофа Gr и критерий Прапдтля Рг.

Критерий Gr характеризует относительную эффективность подъемной силы, вызывающей свободно-конвективное движение среды, и имеет вид

где g — ускорение свободного падения, м 2 /с; (3 — температурный коэффициент объемного расширения среды, 1/К; At — характерная разность температур, °С; / — характерный линейный размер системы, м; v — коэффициент кинематической вязкости, м 2 /с.

Разность температур At определяется в двух точках, например вдали от нагретого тела /_жив точке на его поверхности / .

Уравнения подобия или критериальное уравнение для процессов теплообмена при свободной конвекции имеет вид

Критериальное уравнение для определения среднего по вертикальной поверхности высотой И коэффициента теплоотдачи следующее:

— при (ламинарный режим)

— при (турбулентный режим)

Для газов Рг = const, а Рг_ж/Рг_с = 1, и поэтому приведенные выше формулы упрощаются.

В табл. 1.2 приведены ориентировочные коэффициенты конвективной теплоотдачи для различных задач.

Таблица 1.2. Приближенные значения коэффициента конвективной теплоотдачи

Вид конвекции и среда

Свободная конвекция, воздух

Свободная конвекция, вода

Вынужденная конвекция, воздух

Вынужденная конвекция, вода

Конденсирующийся водяной пар

Конвективный теплообмен при кипении и конденсации сопровождается фазовыми превращениями. Вследствие этого коэффициенты теплообмена имеют большие значения.

📹 Видео