Наиболее широко в химической промышленности используется перемешивание механическими мешалками, которые совершают или вращательное, или возвратно-поступательное движение. При этом тело обтекается потоком жидкости (внешняя задача гидродинамики).
Для расчета мощности мешалок используют критериальное уравнение:

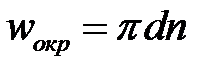
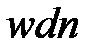
Мешалка подобно насосу создает поток жидкости с сечением S и скоростью ωокр. Поэтому полезная мощность 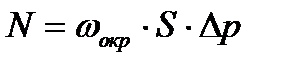
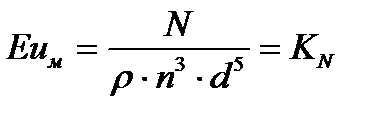
KN – критерий мощности; ∆р – перепад давления перед лопастью и за ней.

На основании опытов построены графики 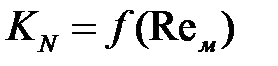
По предварительно выбранным параметрам мешалки определяют Euм: Для выбранного типа мешалки по EUм находят Reм (по графику). Затем вычисляют число оборотов мешалки: При вращении мешалки жидкость может двигаться радиально (вдоль радиуса вращения), тангенциально (по касательной к окружности, описываемой концом мешалки) и в осевомнаправлении вдоль оси вала. Применяются лопастные, пропеллерные, турбинные и специальные мешалки. Лопастные мешалки имеют 2 или более прямоугольные лопасти | ||||
| Лопастная мешалка: 1 – вал, 2 – лопасти. |
Достоинства – простота и дешевизна. Недостаток – слабое осевое перемешивание.
Разновидности лопастных – якорные, рамные, листовые мешалки.
Для более интенсивного перемешивания применяются быстроходные (n = 40 об/с) пропеллерные мешалки. Они обеспечивают преимущественно осевые потоки. Используются для маловязких смесей. Достоинство – высокая интенсивность. Недостатки – сложность изготовления и дороговизна.
Турбинные мешалки также быстроходны (n = 2-5 об/с). Они имеют 4-12 вертикальных прямоугольных лопастей, радиально закрепленных на горизонтальном диске. Если лопасти закрыты, то турбинная мешалка аналогична колесу центробежного насоса с двусторонним всасыванием жидкости. Турбинные мешалки создают преимущественно радиальные потоки и обеспечивают интенсивное перемешивание в большом интервале вязкостей. Лопасти турбинных мешалок могут быть также наклонные или криволинейные.
Недостаток – сложность изготовления мешалки.
Для высоковязких жидкостей – шнековые или ленточные мешалки.
Ограниченно применяются барабанные, дисковые и вибрационные мешалки.
Видео:6.2 Кинематический расчет приводаСкачать
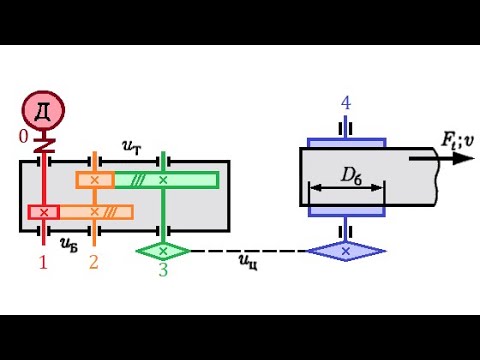
Расход энергии при механическом перемешивании
Перемешивание — это процесс многократного перемещения макрообъёмов текучей среды друг относительно друга во всём объёме аппарата, протекающий за счёт импульса, передаваемого среде механической мешалкой, струёй жидкости или газа.
Процесс перемешивания широко используется в пищевой промышленности при приготовлении суспензий, эмульсий, для интенсификации процессов нагрева и охлаждения обрабатываемых систем, а так же для интенсификации процессов массообмена в перемешиваемой среде.
Наибольшее распространение в настоящее время получили механические мешалки различных типов (лопастные, пропеллерные, турбинные, якорные, шнековые). При перемешивании такими мешалками возникает сложное трёхмерное движение перемешиваемой среды. Основным является тангенциальное движение, которое вызывает в объёме аппарата радиальные и аксиальные потоки. Сложный характер движения среды в аппарате не позволяет получить аналитического описания процесса, поэтому для описания процесса при установившемся режиме пользуются различными критериальными уравнениями, полученными методами теории подобия.
Важной характеристикой работы любой механической мешалки является расход энергии на вращение рабочего элемента мешалки при известных её размерах и заданных физических свойствах среды. Мощность, потребляемая мешалками, зависит от многих факторов. Методы и расчётные формулы, принятые в настоящее время для определения мощности, ещё не могут считаться достаточно полными. Это обстоятельство обуславливает необходимость проведения экспериментальных исследований, на основе которых затем получают необходимые критериальные уравнения.
Процесс перемешивания с гидродинамической точки зрения может быть рассмотрен как процесс внешнего обтекания тела потоком вязкой жидкости, следовательно, можно получить общее критериальное уравнение, описывающее этот процесс:




Г1 = H/d – симплекс геометрического подобия, Н – уровень среды в аппарате, м
Г2 = D/d – симплекс геом. подобия, D – диаметр аппарата.
Таким образом, обобщенная зависимость для определения мощности на валу мешалки при условии геометрического подобия будет иметь вид:
где: с, к. т — экспериментально определяемые величины.
В случаях, когда на поверхности среды не образуется воронка, например, при установке отражательных перегородок или при погружении рабочего элемента мешалки на достаточную глубину, влиянием силы тяжести можно пренебречь и из уравнения (2) исключить критерий Фруда. Тогда обобщённое уравнение для определения мощности, потребляемой мешалкой, примет вид
Температурное поле, температурный градиент.
Температурное поле
совокупность значений температур во всех точках рассматриваемого пространства в данный момент времени. Математически Т. п. может быть описано уравнением зависимости температур от 3 пространственных координат и от времени (нестационарное трёхмерное Т. п.). Для установившихся (стационарных) режимов Т. п. от времени не зависит. Во многих случаях может рассматриваться зависимость Т. п. от двух, а иногда от одной координаты. Графически Т. п. изображают посредством изотермических поверхностей, соединяющих все точки поля с одинаковой температурой, а для двухмерного поля — посредством семейства изотерм (См. Изотерма). Расстояние между изотермами обратно пропорционально Градиенту температуры; при этом скалярному Т. п. соответствует векторное поле градиентов температуры
Будем рассматривать только однородные и изотропные тела, т.е. такие тела, которые обладают одинаковыми физическими свойствами по всем направлениям. При передачи теплоты в твердом теле, температура тела будет изменяться по всему объему тела и во времени.
Совокупность значений температуры в данный момент времени для всех точек изучаемого пространства называется температурным полем:
где: t –температура тела;
x,y,z -координаты точки;
Такое температурное поле называется нестационарным ∂t/∂i ¹ 0, т.е. соответствует неустановившемуся тепловому режиму теплопроводности.
Если температура тела функция только координат и не изменяется с течением времени, то температурное поле называется стационарным:
t = f(x,y,z) , ∂t/∂i = 0 (9.2)
Уравнение двухмерного температурного поля:
для нестационарного режима:
t = f(x,y,τ) ; ∂t/∂z = 0 (9.3)
для стационарного режима:
t = f(x,y) , ∂t/∂z = 0; ∂t/∂i = 0 (9.4)
Уравнение одномерного температурного поля:
для нестационарного режима:
t = f(x,τ) ; ∂t/∂y = ∂t/∂z = 0; ∂t/∂i ¹ 0 (9.5)
для стационарного режима:
t = f(x) ; ∂t/∂y = ∂t/∂z = 0; ∂t/∂i = 0 (9.6)
Изотермической поверхностью называется поверхность тела с одинаковыми температурой.
Рассмотрим две изотермические поверхности (Рис.9.1) с температурами t и t + ∆t.
Градиентом температуры называют предел отношения изменения температуры ∆t к расстоянию между изотермами по нормали, когда ∆n стремится к нулю:
ЧТО ПРОИСХОДИТ ВО ВЗРОСЛОЙ ЖИЗНИ? Если вы все еще «неправильно» связаны с матерью, вы избегаете отделения и независимого взрослого существования.
Что способствует осуществлению желаний? Стопроцентная, непоколебимая уверенность в своем.
Живите по правилу: МАЛО ЛИ ЧТО НА СВЕТЕ СУЩЕСТВУЕТ? Я неслучайно подчеркиваю, что место в голове ограничено, а информации вокруг много, и что ваше право.
Конфликты в семейной жизни. Как это изменить? Редкий брак и взаимоотношения существуют без конфликтов и напряженности. Через это проходят все.
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
Видео:Расчет режимов: Схемы выдачи мощности, расчетов параметров ЛЭПСкачать

Критериальное уравнение для расчета мощности мешалок
С четырьмя перегородками шириной 0,1 D
Открытая турбинная с шестью плоскими лопатками
Открытая турбинная с шестью плоскими лопатками
С четырьмя перегородками шириной 0,1 D
Открытая турбинная с восемью плоскими наклонными лопатками
С четырьмя перегородками шириной 0,1 D
Закрытая турбинная с шестью лопатками
Закрытая турбинная с шестью лопатками и направляющим аппаратом
Дисковая с шестью лопатками
С четырьмя перегородками шириной 0,1 D
Примечание D диаметр сосуда, Н высота слоев жидкости в мешалке, b ширина лопастей мешалки, s шаг винта, l длина лопасти, d , d тр , d зм диаметр соответственно мешалки, трубы и змеевика, t шаг змеевика.
Процесс перемешивания механическими мешалками сводится к внешней задаче гидродинамики обтеканию тел потоком жидкости.
При медленном движении в вязкой среде тела любой формы в тонком слое жидкости, примыкающем к его поверхности, образуется ламинарный пограничный слой, форма и толщина которого зависят от формы и размеров тела, скорости и физических свойств жидкости.
При увеличении скорости движения происходит отрыв пограничного слоя от поверхности тела в точках, где скорость жидкости является наибольшей, например у кромок вертикальной пластины, и образование турбулентного кормового следа за движущимся телом. Начало отрыва пограничного слоя характеризуется резким возрастанием сопротивления среды движению тела.
Окружная скорость имеет наибольшее значение на периферии мешалки, так как эта величина пропорциональна диаметру мешалки. У периферии мешалки образуется зона пониженного давления, куда устремляется жидкость, находящаяся в аппарате. Это течение, а также радиальные потоки, возникающие под действием центробежных сил при вращательном движении мешалки, приводят к интенсивному перемешиванию содержимого аппарата.
Задача внешнего обтекания тел в условиях перемешивания может быть решена с помощью уравнений Навье-Стокса и неразрывности потока. Точное аналитическое решение указанной задачи весьма сложно и возможно лишь для частных случаев. Поэтому для решения этой задачи используют теорию подобия.
Мощность, потребляемая мешалками при перемешивании, зависит от размеров мешалки и аппарата, размера и числа отражательных перегородок, физических свойств перемешиваемой среды, скорости мешалки.
Вместо линейной скорости жидкости, среднее значение которой при перемешивании установить практически невозможно, в расчётах подставляется величина nd , пропорциональная окружной скорости мешалки ω окр :
где п число оборотов мешалки в единицу времени;
d диаметр мешалки.
Для определения расхода энергии при механическом перемешивании пользуются методом анализа размерностей.
Безразмерный комплекс называется критерием Эйлера Е u м или критерием мощности К N для механического перемешивания. Критерий является центробежным (модифицированным) критерием Рейнольдса и обозначается .
Уравнение (2) является критериальной зависимостью для расхода энергии при механическом перемешивании. Коэффициент С и показатель степени m определяют экспериментально.
Для наиболее распространенных типов мешалок зависимости представлены графически (рис.2).
Рисунок 2 Зависимость критерия мощности от критерия Рейнольдса
Пояснения к рисунку 2:
1 открытая турбинная мешалка с шестью прямыми вертикальными лопатками ( b = =0,20 d м ; l = 0,25 d м ) при D / d м = 3 в сосуде с четырьмя перегородками ( B / d м = 0,17); 2 турбинная мешалка типа 1 при B / d м = 0,10; 3 -открытая турбинная мешалка с шестью изогнутыми вертикальными лопатками ( b = 0,20 d м , l = 0,25 d м ) при D / d м = 3 в сосуде с четырьмя перегородками ( B / d м = 0,10); 4 турбинная мешалка типа 1 при B / d м = 0,04; 5 открытая турбинная мешалка с шестью стреловидными лопатками ( b = 0,20 d м , l = 0,25 d м ) при D / d м = 3 в сосуде с четырьмя перегородками ( B / d м = 0,10); 6 односторонняя радиально-дисковая мешалка с шестью прямыми вертикальными лопатками ( b = 0,10 d м , l = 0,35 d м ) снизу диска при D / d м = 2,5 в сосуде с четырьмя перегородками ( B / d м = 0,25);7 радиальная турбинная мешалка с шестнадцатью лопатками со статором в сосуде без перегородок; 8 -двухлопастная мешалка с прямыми вертикальными лопастями ( b = 0,25 d м ) при D / d м = 4,35 в сосуде с тремя перегородками ( B / d м = 0,11); 9 восьмилопастная мешалка с прямыми лопастями ( b = 0,25 d м ) под углом 45 о при D / d м = 3 в сосуде с четырьмя перегородками ( B / d м = 0,10); 10 двухлопастная мешалка типа 8 при D / d м = 3 в сосуде с четырьмя перегородками ( B / d м = 0,10); 11 закрытая турбинная мешалка с шестью лопатками со статором при D / d м = 2,4 в сосуде без перегородок; 12 -турбинная мешалка, сходная с типом 11 при D / d м = 3 в сосуде без перегородок; 13 -турбинная мешалка типа12 , без статора при D / d м = 3 в сосуде с четырьмя перегородками ( B / d м = 0,10); 14 -турбинная мешалка типа 1 в сосуде без перегородок; 15 -трехлопастная пропеллерная мешалка s =2 d м при D / d м = 3 в сосуде с четырьмя перегородками ( B / d м = 0,10); 16 четырехлопастная мешалка типа 8 при D / d м = 3 в сосуде без перегородок; 17 -четырехлопастная мешалка с лопастями ( b = 0,25 d м ) под углом 60° при D / d м = 3 в сосуде без перегородок; 18 -трехлопастная пропеллерная мешалка типа15 , но при s = l ,33 d м и D / d м = 16 в сосуде с тремя перегородками ( B / d м = 0,06); 19 четырехлопастная мешалка типа 9 при D / d м = 5,2 в сосуде без перегородок; 20 двухлопастная мешалка типа 8 при D / d м = 3 в сосуде без перегородок; 21 трехлопастная пропеллерная мешалка типа 15 при D / d м = 3,3 в сосуде без перегородок;22 четырехлопастная мешалка типа 9 (такая же, как19 ) при D / d м = 2,4÷3,0 в сосуде без перегородок; 23 трехлопастная пропеллерная мешалка типа 15 при s = 1,04 d м и D / d м = 9,6 в сосуде с тремя перегородками ( B / d м = 0,06); 24 то же при s = d м и D / d м = 3 в сосуде с четырьмя перегородками ( B / d м = 0,10); 25 то же при s = 1,04 d м и D / d м = 4,5 в сосуде без перегородок; 26 то же при s = d м и D / d м = 3 в сосуде без перегородок; 27 то же при s = 1,05 d м и D / d м = 2,7 в сосуде без перегородок; 28 то же при s = d м и D / d м = 3,8 в сосуде без перегородок; 29 двухлопастная мешалка типа 8 с узкими лопастями [ b = (0,13÷0,17) d м ] при D / d м =1,1 в сосуде без перегородок.
Обозначения, принятые для характеристики мешалок: D диаметр сосуда; d м диаметр мешалки; b -ширина лопасти мешалки; l -длина лопасти; В ширина перегородки; s шаг пропеллерной мешалки.
В общем случае критерий мощности зависит не только от критерия , но и от модифицированного критерия Фруда:
Исследования, проведенные по выявлению влияния критерия Фруда на потребляемую мощность показали, что для мешалок различного типа, как в аппаратах с отражательными перегородками, так и в гладкостенных аппаратах, мощность не зависит от критерия Фруда при значениях критерия Рейнольдса: Re м Re кр , где Re кр критическое значение критерия Рейнольдса, при котором воздушная воронка достигает лопастей мешалки и начинается аэрация жидкости, вследствие чего происходит изменение вязкости и плотности перемешиваемой среды.
Таким образом, связь между энергией, затрачиваемой в единицу времени, и условиями перемешивания выражают в виде зависимости:
Описание экспериментальной установки:
Установка для исследования процесса перемешивания изображена на рис.3. Она содержит стеклянный сосуд 1 с установленными на его внутренней поверхности отражательными перегородками 2 . В сосуде 1 на вертикальном валу 3 устанавливаются турбинная мешалка 4 (открытого или закрытого типа), которая приводится в действие электродвигателем 5 . С помощью лабораторного автотрансформатора (ЛАТР) 9 обеспечивается плавное изменение частоты вращения мешалки 4 от 0 до 600 об/мин.
При проведении опытов измеряют частоту вращения вала мешалки цифровым автоматическим тахометром (ЦАТ-2М) 8 при помощи фотоэлектрического датчика 7 , включающего излучатель с фотоэлементом, и диска 6 с отверстиями жестко закрепленного на валу 3 .
Потребляемая мощность измеряется ваттметром 10 , подключенным к электродвигателю 5 .
Методика проведение работы
1) Заполняют стеклянный сосуд 1 жидкостью до определенного уровня и измеряют температуру жидкости.
2) Включают электродвигатель 5 привода мешалки 4 .
3) С помощью лабораторного автотрансформатора 9 устанавливают минимальную частоту вращения вала 3 мешалки 4 и ваттметром 10 замеряют потребляемую мощность.
4) Автоматическим тахометром 8 измеряют частоту вращения мешалки 4 .
5) Последовательно изменяя частоту вращения мешалки (6-8 раз), повторяют замеры.
6) После окончания экспериментов отключают все приборы.
1 стеклянный сосуд, 2 отражательные перегородки, 3 вал, 4 мешалка, 5 электродвигатель, 6 диск с прорезями, 7 фотоэлектрический датчик, 8 автоматический тахометр ЦАТ-2М, 9 лабораторный автотрансформатор, 10 ваттметр.
Рисунок 3 Схема экспериментальной установки
Обработка опытных данных
Рассчитать для каждой частоты вращения критерий мощности K N , центробежный критерий Рейнольдса Re м .
Построить график зависимости lgK N = f ( lgRe ) (рис.4) и по этому графику определите значения постоянных величин C и m , входящих в формулу
Логарифмируя эту формулу, получают уравнение прямой линии
Показатель степени m находят как тангенс угла наклона полученной прямой . Так как угол расположен во второй четверти, то его величина будет отрицательной.
Постоянная С находится как отрезок, отсекаемый прямой на оси ординат, или из уравнения
Необходимо сделать не менее трех таких определений и получить из них среднее значение коэффициентов.
Рисунок 4 График критериальной зависимости
Таблица 2 Данные измерений и расчетов
Частота вращения мешалки
Критерий мощности К N
Критерий Рейнольдса центробежный Re м
Отчет о работе должен содержать : схему установки, расчетные формулы, таблицу измеренных и рассчитанных величин, графики зависимостидля исследуемых типов мешалок, вычисление значений показателя степени m и коэффициента С из уравнения (7), выводы по работе.
Контрольные вопросы к работе
1. Назначение процесса перемешивания.
2. Способы перемешивания в жидких средах.
3. Типы наиболее широко применяемых мешалок, их основные достоинства и недостатки.
4. Физический смысл критерия мощности.
5. С какой целью применяются отражательные перегородки?
6. Что понимают под интенсивностью и эффективностью процесса перемешивания?
7. Почему при характеристике работы мешалок скорость движения жидкости в аппаратах заменяют произведением частоты вращения на диаметр мешалки?
8. Вид и значение общего критериального уравнения.
Список использованных источников
1.Кавецкий Г.Д., Васильев Б.В. Процессы и аппараты пищевой технологии. М.:Колос,1999. 551с.
2.Касаткин А.Г. Основные процессы и аппараты химической технологии. М.: Химия, 1971. 783с.
3.Васильцов Э.А., Ушаков В.Г. Аппараты для перемешивания жидких сред: Справочное пособие. Л.: Машиностроение, 1979. 269с.
Лабораторная работа №2
Изучение работы циклона
Практическое ознакомление с работой пылеулавливающего циклона, исследование зависимости эффективности улавливания циклона () и его гидравлического сопротивления (ΔР ц )от условной скорости газового потока; определение коэффициента гидравлического сопротивления циклона.
При переработке пищевого сырья, получении полуфабрикатов и готового продукта в промышленности образуются пыли взвешенные в газах мелкодисперсные твёрдые частицы. Отходящие промышленные газы, содержащие пыли, подвергают пылеочистке, путём осаждения твёрдых частиц под действием различных сил: тяжести, центробежных, электростатических, и других.

Процесс разделения неоднородных систем «Газ-твёрдые частицы» под действием центробежных сил обуславливается разностью плотностей газового потока и Рисунок 1 Циклон
твёрдых частиц, находящихся во вращательном движении. Центробежные силы, возникающие при этом, обеспечивают большуюэффективность процесса по сравнению с процессом разделения, проходящим в поле только сил тяжести.
Соотношение этих сил называют фактором разделения или центробежным критериемФруда (Fr):
где: mg сила тяжести, Н;
Р ц центробежная сила, отбрасывающая твёрдую частицу из вращающегося потока газовзвеси к стенкам аппарата:
где: m масса частицы;
υ окружная скорость, м/с;
R радиус аппарата, м.
Фактор разделения характеризует увеличение разделяющей способности в условиях действия центробежной силы:
Из выражения (3) видно, что эффективность разделения возрастает с увеличением скорости газового потока и уменьшением радиуса аппарата. Однако значительное увеличение скорости связано с резким возрастанием гидравлического сопротивления циклона и усилением местных завихрений, срывающих уже осевшие на внутренней поверхности циклона твёрдые частицы, что приводит к снижению эффективности улавливания частиц из газового потока (наиболее эффективными являются скорости газа на входе в циклон в интервале 18…25 м/с). Уменьшение радиуса циклона приводит к снижению его производительности. Поэтому часто для очистки больших количеств запыленных газов вместо циклона большого диаметра применяют несколько циклонных элементов значительно меньшего диаметра (их монтируют в одном корпусе). Такие циклоны называются батарейными циклонами, или мультициклонами (рисунок 2).
Процессы, происходящие в циклоне, весьма сложны и зависят от многих факторов, поэтому при теоретических расчётах приходится делать много допущений и упрощений.
Так, принимают, что пылевые частицы, поступающие с воздушным потоком в циклон, имеют сферическую форму, при входе запыленного потока в циклон равномерно распределены по сечению, а также то, что частицы, которые при перемещении достигли стенок, подвергаются осаждению, хотя в действительности часть этих частиц будет выброшена в выхлопную трубу вследствие турбулизации потока и т.д. Кроме того, не учитывается такой фактор, как коагуляция частиц, происходящих в циклоне.
Вследствие ряда упрощений и допущений расчёт циклона весьма приближенный. Поэтому при разработке новых конструкций циклонов необходимо в значительной мере учитывать экспериментальные данные и опыт эксплуатации циклонов в производственных условиях.
1 корпус циклона;2 входной патрубок; 3 газораспределительная камера;
4 трубные решетки; 5 циклонные элементы; 6 выходной патрубок для очищенного газа; 7 коническое днище (бункер).
Рисунок 2 Батарейный циклон
Ценность теоретических исследований состоит в том, что они позволяют выявить основные закономерности работы циклонов.
При расчёте обычно получают зависимости, характеризующие радиальную скорость перемещения частиц в циклоне, время пребывания частиц в циклоне, предельный диаметр частиц пыли, улавливаемых в циклоне.
Для получения этих зависимостей рассмотрим движение частицы пыли в циклоне.
На частицу, перемещающуюся с потоком запыленного газа в циклоне, действует центробежная сила Р ц , под действием которой частица перемещается к стенке циклона.
Радиальному перемещению частицы пыли со скоростью оказывает сопротивление газовая среда. Величина этого сопротивления, согласно закону Стокса, равна:
Через некоторое, весьма незначительное время после ввода запыленного потока в циклон центробежная силаP ц уравновешивается силой сопротивления среды P с и частица пыли движется в радиальном направлении к стенкам циклона с постоянной скоростью υ
После подстановки значенийυ и μ
Отсюда можно определить значение , учитывая, что масса частицы m сферической формы равна
Определим время, необходимое для того, чтобы частица пыли совершила путь к стенке корпуса циклона.
Дальше всех от стенки циклона находятся частицы, которые вошли в циклон около выхлопной трубы. Им предстоит пройти в радиальном направлении путь, равный R — R o , где R радиус циклона, м; R o радиус выхлопной трубы, м (рис.1.)
Запишем скорость как производную пути r по времени и, проинтегрировав, найдем время , необходимое для прохождения радиального пути
Степень очистки в циклоне сильно зависит от дисперсного состава частиц пыли в поступающем на очистку газе (чем больше размер частиц, тем эффективнее очистка).Определим размер наименьших частиц пыли, улавливаемых в циклоне.
Поток запыленного газа проходит цилиндрическую часть циклона за промежуток времени 1
где: 2 R ср n путь пройденный запыленным потолком, м ( n число оборотов, совершаемых потоком и цилиндрической части циклона, принимаемое равным 2);
ц скорость потока, м/ c .
Частицы, которые за время 1 не успели пройти радиальный путь, будут унесены с потоком и не отделятся в циклоне. Таким образом, приравнивая время , необходимое для прохождения радиального пути, ко времени 1 , найдем размер наименьших частиц, которые улавливаются в данном циклоне:
Работа циклона оценивается по совокупности двух его основных характеристик:
- эффективности улавливания (эффективности разделения, степени очистки или коэффициента полезного действия);
- гидравлического сопротивления(энергозатрат на пылеочистку).
Понятно, что желаемым является достижение высокой эффективности улавливания при низком гидравлическом сопротивлении.
Эффективность улавливания() может быть определена по известным начальной (С н ) и конечной (С к ) концентрациям твердых частиц в потоке газовзвеси, проходящей через аппарат
где G ул , G н соответственно массовый расход твердых частиц на входе в цикл и на выходе из цикла;
G ул = G н — G к массовый расход уловленных твердых частиц.
Гидравлическое сопротивление циклона можно представить как сумму потерь давления на преодоление сопротивления трения и местных сопротилений (потери при входе в циклон; потери на преодоление трения в корпусе; потери при переходе газового потока из внешней зоны циклона во внутреннюю зону циклона с поворотом на 180 0 С; потери в выхлопной трубе).
Выражая общее гидравлическое сопротивление через динамический напор во входном патрубке, и заменяя сумму частных коэффициентов гидравлических сопротивлений через общий коэффициент гидравлического сопротивления циклона ξ ц , получим
где:-плотность газовой среды при рабочих условиях, кг/ м 3 ;
вх -средняя скорость газа во входном патрубке, м/с.
где: V -объемный расход газа, м 3 / с;
f вх -площадь живого сечения входного патрубка, м 2 .
При расчете величины общего гидравлического сопротивления циклона чаще ее определяют как функцию условной скорости газа, отнесенной к площади свободного поперечного сечения цилиндрической части корпуса циклона:
где: ц условная скорость газа; для обеспечения высокой степени очистки в циклоне принимают ( ц =3…4 м/ c ).
Условная скорость газа в циклоне рассчитывается по уравнению
где: D -диаметр циклона, м.
Значения коэффициентов ξ ц и ξ ц зависят от конструктивных особенностей циклонов.
Выбор типа и размера циклонов производится на основе заданного расхода газов, физико-механических свойств пыли (адгезионных свойств, плотности частиц, их абразивности, дисперсного состава), требуемой степени очистки, габаритов установки, эксплуатационной надежности и стоимости очистки.
Конструкции циклонов разнообразны. Наиболее распространены цилиндрические и конические циклоны конструкции НИИОГАЗа. К цилиндрическим относятся циклоны типа ЦН-11; ЦН-15; ЦН-15У; ЦН-24 (цифры обозначают угол наклона входного патрубка).
К коническимотносятся циклоны типа СДК-ЦН-33,СК-ЦН-34 и СК-ЦН-22 (цифры обозначают отношение диаметров выхлопной трубы и корпуса в процентах). Они отличаются длиной конической частью и спиральным входным патрубком.
Цилиндрические аппараты относятся к высокопроизводительным, а конические- к высокоэффективным.
В настоящее время находят широкое применение пылеуловительные со встречными закрученными потоками (ВЗП).
В отличие от циклонов в аппарат ВЗП газ подается двумя потоками через тангенциальные вводы, снабженные завихрителями (см.рис.3). Запыленный газ может подаваться по одному из каналов, а также по обоим каналам одновременно. Первичный поток газовзвеси входящий через верхний ввод, проходит через периферийную зону аппарата, а вторичный (нижний ввод)- через центральную (приосевую) зону. Под действием центробежных сил частицы перемещаются к стенке аппарата и через зазор между отбойной шайбой и корпусом попадают в бункерную часть аппарата. Очищенный газ выводится через выхлопную трубу.
Рисунок 3 Пылеуловитель со встречными закрученными потоками
Аппараты ВЗП превосходят циклы (типа ЦН и др.), как по эффективности сепарации, так и по экономическим показателям: коэффициент гидравлического сопротивления аппарата ВЗП в 2,7÷3 раза,а удельные энергозатраты на 20÷40% ниже, чем у циклона. Эффективность улавливания у аппарата ВЗП на 4÷6% выше, чем у циклона.
Описание экспериментальной установки
Лабораторная установка, схема которой изображена на рисунке 4 состоит из циклона 4 (внутренний диаметр циклона 0,2м, размер входного патрубка 0,130,05 м, внутренний диаметр выхлопной трубы 0,12 м), который установлен после аппарата взвешенного (псевдоожиженного слоя). Частицы твердого материала, уносимые из слоя, попадают через систему воздуховодов во входной тангенциальный патрубок циклона. Условленные в циклоне частицы материала собираются в сборнике. Расход воздуха регулируется при помощи заслонки.
В качестве измерительных приборов использованы: трубка Пито-Прандтля, подсоединенная к микроманометру ММН-240, служащая для определения расхода воздуха; дифференциальный манометр для определения гидравлического сопротивления циклона.
1 вентилятор; 2 аппарат кипящего слоя; 3 аппарат фонтанирующего слоя; 4 циклон; 5 сборник уловленного материала; 6,7 поворотные краны; 8,9 трубки Пито-Прандтля; 10 блок U -образных манометров; 11 газораспределительная решётка; 12,13 сетки; 14 мерная линейка
Рисунок 4 Схема экспериментальной установки
Методика проведения работы
Эксперименты по исследованию работы циклона проводят в два этапа. На первом этапе определяют гидравлическое сопротивление циклона в зависимости от расхода, незапыленного газового потока; на втором — эффективность улавливания циклона в зависимости от расхода газового потока при постоянной концентрации твердых частиц в нем.
На первом этапе исследование циклона проводят на не запыленном воздухе. Включают вентилятор и устанавливают с помощью заслонки необходимый расход воздуха в пределах, заданных преподавателем (5…7 значений расходов). При установленном расходе воздуха снимают показания микроманометра ММН-240 и дифференциального манометра, которые заносят в таблицу 1.
На втором этапе определяют эффективность улавливания циклона при различных значениях расхода воздуха. Для этого в аппарат взвешенного слоя, работающий в режиме пневмотранспортёра, вводят постоянно одно и тоже количество материала и измеряют количество материала, уловленного в циклоне. Опыты повторяют 5….7 раз при различных расходах воздуха с сохранением постоянной концентрации твердых частиц в газовом потоке. Полученные в каждом опыте данные заносят в таблицу 1.
Обработка опытных данных и составление отчета
По результатам экспериментов для каждого опыта определяют:
1.Расход воздуха V , м 3 / c
2.Скорость газового потока во входном патрубке циклона вх и условную скорость газового потока в циклоне ц по уравнениям (15) и (16)
3.Коэффициенты гидравлических сопротивлений и по уравнениям (14) и (16)
5.Эффективность улавливания циклона по уравнению (13)
По результатам расчета необходимо построить:
1) График зависимости
2) График зависимости =, определить оптимальную скорость воздуха, соответствующую высокой эффективности улавливания при малом гидравлическом сопротивлении циклона.
Таблица 1 Результаты измерений
Показание дифманометраприсоединён-ного к циклону
на входе в циклон
Объём-ный расход воздуха, V ,м 3 /с
Скорость воздуха во входном патрубке циклона, , м/с
Условнаяскорость воздуха в циклоне
Контрольные вопросы к работе
- Перечислите аппараты, применяемые для улавливания пыли?
- Устройство и принцип работы циклона?
- Что понимают под фактором разделения?
- За счет чего в циклоне возникает центробежная сила?
- Как влияет диаметр циклона и скорость газового потока на его разделяющую способность?
- С какой целью в промышленной практике прибегают к применению батарейных циклонов?
- Что понимают под гидравлическим сопротивлением циклона и как его рассчитать?
- Что понимают под степенью очистки циклона?
Лабораторная работа № 3
Определение констант фильтрования
Определение констант процесса фильтрования и производительности фильтра по фильтрату.
Процессом фильтрования называют разделение суспензий, пыли или тумана путём пропускания их через пористую перегородку-фильтр, способную задерживать взвешенные частицы (дисперсную среду), образуя осадок, но пропускать жидкость или газ (дисперсную среду), образуя фильтрат (либо очищенный газ).
Скорость фильтрования суспензий существенным образом зависит от физических свойств жидкости и крупности твёрдых частиц и их концентрации. По степени крупности твёрдых частиц суспензии делят на:
а) грубые (размер частиц более 100 мкм);
б) тонкие (размер частиц от 100 до 0,5 мкм);
в) мути (размер частиц до 0,5 мкм);
г) коллоидные растворы.
На практике встречаются все виды суспензий и большей частью с частицами разных размеров, т.е. полидисперсные системы.
При фильтровании суспензия поступает на пористую фильтрующую перегородку, через которую жидкая фаза проходит, а взвешенные частицы остаются на поверхности фильтра в виде осадка.
- С образованием осадка;
- С закупориванием пор;
- Промежуточный вид;
Для движения жидкости в порах осадка и фильтрующей перегородки необходимо создать перепад давления над и под фильтрующей перегородкой.
Перепад давления над и под фильтрующей перегородкой является движущей силой процесса и создается за счет разряжения под фильтрующей перегородкой (вакуум-фильтры) или создания давления над фильтрующей перегородкой (фильтры под давлением).
Существует 4 основные характеристики фильтрования: движущая сила процесса, скорость процесса, производительность фильтра, константы процесса фильтрования.
Производительность фильтра зависит от режима фильтрования (давление, температура), вида фильтрующей перегородки и физико-химических свойств суспензии и осадка.
Фильтрование со сжимаемым и несжимаемым осадком:
- Несжимаемые осадки пористость которых не меняется при увеличении давлений (мел, песок);
- Сжимаемые осадки пористость уменьшается, гидравлическое сопротивление потоку жидкой фазы возрастает с увеличением давления (гидраты окисей металлов).
Хорошая работа фильтра во многом зависит от свойств фильтрующей перегородки, которую изготавливают из различных хлопчатобумажных тканей (бельтинг, бязь, миткаль, диагональ и др.), шерстяных тканей (сукно, байка, войлок), тканей из синтетических волокон (поливинилхлоридные, перххлорвиниловые, полиамидные, орлон, лавсан, и до.), тканей из волокон минерального происхождения (асбестовые и стеклянные) и др. В последнее время всё шире начинают применять пористые металлические, керамические и металлокерамические фильтрующие перегородки.
Выбор той или иной фильтрующей перегородки обусловлен:
1. Пористостью (размеры пор должны быть такими, чтобы частицы осадка задерживались на перегородке);
2. Химической стойкостью к действию фильтруемой среды;
3. Достаточной механической прочностью;
4. Теплостойкостью при температуре фильтрования.
Рассматривая параметры, влияющие на процесс фильтрования, можно написать в общем виде закон фильтрования:
где V производительность единицы поверхности фильтрующей перегородки по фильтрату, м 2 /м 3 за время (в ч., мин., с.);
скорость фильтрования м 3 /м 2 ч;
ΔР движущая сила процесса фильтрования (перепад давлений), Н/м 2 ;
R сопротивление фильтрования Н·с/м 3 .
Движущей силой процесса фильтрования ΔР является разность давлений по обе стороны фильтрующей перегородки. Разность давлений может быть создана:
а) слоем самой суспензии, налитой на фильтр;
б) подачей суспензии на фильтр насосами (например, в фильтр-прессах давление достигает 0,5 Мпа);
в) создание вакуума под фильтрующей перегородкой, либо избыточного давления газа над фильтрующей перегородкой (например, в промышленном вакуум-фильтрах вакуум составляет 0,095 Мпа, а давление газа до 0,3 Мпа);
г) наложением на разделяемую суспензию центробежного поля, движущая сила при этом принимает максимальное значение и достигает 1,5 МПа.
Сопротивление фильтрования R складывается из сопротивления осадка R ос и сопротивления фильтрующей перегородки R п , т.е.:
Сопротивление слоя осадка пропорционально количеству отложившейся твёрдой фазы и, следовательно, пропорционально количеству прошедшего фильтрата, R OC = K ′ V
Сопротивление фильтрующей перегородки можно заменить сопротивлением слоя осадка, оказывающего такое же сопротивление процессу фильтрования, какое оказывает перегородка, и выразить соответствующим количеством фильтрата С, т.е:
где K ′ коэффициент пропорциональности.
Подставив полученное значение R в уравнение (1), разделив переменные и проинтегрировав, после небольших преобразований получим уравнение фильтрования:
где: µ вязкость фильтрата, Н·с/м 2 ;
r 0 удельное сопротивление осадка;
х 0 концентрация суспензии, м 3 / м 3 .
Зависимость (5) является основным кинетическим уравнением процесса фильтрования и показывает зависимость объёма фильтрата V продолжительности фильтрования τ.
Расчёт промышленных фильтров обычно сводится к определению требуемой поверхности фильтрования F . Для этого, зная константы фильтрования К и С и продолжительность фильтрования τ, назначаемую из условий: обеспечения требуемой остаточной влажности осадка ω, из уравнения (5) определяют удельную производительность по фильтрату V , м 3 /(м 2 ·с). Затем рассчитывают секундную производительность по фильтрату V c , м 3 /(м 2 ·с).
Зная производительность промышленной фильтрационной установки по фильтрату V ф , находят требуемую площадь фильтровальной перегородки F , м 2 :
Для определения констант фильтрования К и С опытным путём продифференцируем уравнение (5):
2 VdV +2 CdV = Kdτ
и, разделив обе части уравнения на KdV , получим:
Заменяя отношение бесконечно малых величин на отношение конечных разностей, получим уравнение, пригодное для обработки опытных данных:
Это уравнение прямой линии типа y = kx + b , свободный член которого b =2 C / K .
При построении уравнения (7) в координатах , отрезок, отсекаемый на оси координат, даёт численное значение свободного члена, а тангенс угла наклона прямой tgα =.
Для определения постоянных процесса фильтрования K и C проводят опыт по разделению исследуемой суспензии на фильтрате при постоянной разности давлений.
В течение опыта отмечают несколько значений объёма полученного фильтрата V 1 , V 2 , V 3 , … V n и продолжительности фильтрования τ 1 , τ 2 , τ 3 … τ n . Определяют приращения объёма фильтрата , ,. . ., и приращения продолжительности фильтрования , , . . ., , после чего вычисляют отношение для всех случаев.
Зависимость величин, обратной скорости фильтрования, от объёма фильтрата V
Рисунок 1 Зависимость величин, обратной скорости фильтрования Δτ/Δ V от объёма фильтрата V .
Для построения прямой в координатах (рис.1) на оси абсцисс откладывают величины V 1 , V 2 , V 3 , ….. V n и из полученных точек восстанавливаю перпендикуляры.
На каждом перпендикуляре откладывают соответствующее отношение приращений . Из полученных таким образом точек, проводят горизонтальные отрезки до пересечения с левым соседним перпендикуляром. Прямую проводят через середины отрезков , и т.д., что соответствует примерно средней производительности по фильтрату в диапазонных изменения V от 0 до V 1 , от V 1 до V 2 , от V 2 до V 3 и т.д. для соответствующих приращений величина, обратная уменьшению скорости фильтрования. Прямую проводят до пересечения с осями ординат и абсцисс. Построив эту прямую по экспериментальным данным, можно определить константы фильтрования К и С.
Объёмная скорость прохода жидкости через фильтр, или скорость фильтрования, величина переменная, непрерывно уменьшающаяся, которую для заданного момента времени от начала фильтрования определяют на основании уравнения (7), как:
Установка для экспериментального определения констант процесса фильтрования c одержит бак для приготовления суспензии 1 с отражательными перегородками 2 и соосно-расположенной мешалкой 3. Разборный вакуум фильтр 4 состоит из двух выпуклых крышек, между которыми закрепляется фильтровальная перегородка 5, опирающаяся на опорную (дренажную) сетку.
Методика проведения работы
Приготавливают суспензию с заданным соотношением твёрдой и жидкой фаз в количестве, указанном преподавателем,и заливают в бачок I , предварительно закрыв вентиль II и включив привод мешалки. Затем включают вакуум-насос 10 и, медленно открывая запорный вентиль 9,устанавливают заданный преподавателем вакуум по вакуумметру 8.
После этого открывают кран II и одновременно включают секундомер. Через некоторое время, когда в приёмник 6 наберётся некоторое количество фильтрата, производят (не включая секундомера) одновременный замер времени и собранного фильтрата V . Такие замеры производят несколько раз. Затем процесс фильтрования прекращают, выключают вакуум-насос и секундомер и записывают время и объём фильтрата.
1-бачок для суспензии;2-рамная мешалка; 3-отражательгые перегородки; 4-вакуум фильтр;5- фильтровальная перегородка; 6-приёмник фильтрата; 7-указатель уровня фильтра;8-вакууметр; 9- вентилятор запорный;10-вакуум-насос.
Рисунок 2 Схема установки для определения констант процесса фильтрования
Обработка опытных данных
По полученным замерам объёмов V 1 ,…, Vn и времени определяют разности и и вычисляют отношения ,…,.Затем строят график, откладывая по оси абсцисс величины измеренных объёмов от V 1 ,до V n , а по оси ординат величины этих отношений от до . Так как отношения является средне величиной для соответствующих интервалов ,то величины этих соотношений следует откладывать по вертикали из серидины однозначных интервалов, либо проводят прямую через середины отрезков , и т.д., как об этом сказано выше.
Для определения константы К находим тангенс угла наклона прямой DE (см.рис. I ) как отношение катетов, взятых в соответственных масштабах:
Из выражения находим константу фильтрования К
Константу С находим непосредственно по замерам отрезка по рисунку I .
Для получения правильных результатов в системе СИ время и должно быть представлено в секундах, а объёмы фильтрата V и V пересчитаны в удельные объёмы, выраженные в м 3 , отнесённые к площади фильтрата, выраженной в м 2 , м 3 /м 2 .
Далее определяют скорости фильтрования в начальный и конечный моменты:
Таблица 1 Результаты измерений
Производительность по фильтрату
- Какие параметры входят в основное дифференциальное уравнение фильтрования?
- Что такое удельное сопротивление осадка?
- Чем может быть создана движущая сила процесса фильтрования?
- Какие данные необходимо иметь для инженерного расчёта фильтра?
- Как объяснить влияние давления на удельное сопротивление осадка?
- Почему при подаче суспензии на фильтр центробежными насосами движущая сила процесса фильтрования монотонно увеличивается, но производительность фильтра падает? Как можно исправит это положение, т.е., чтобы производительность фильтра оставалась постоянной?
- Как изменится чистота фильтрата в аппаратах с периодическим удалением слоя осадка?
- Какие достоинства (недостатки) гибких фильтровальных перегородок (ФП) по сравнению с жёсткими (негибкими) ФП?
- Как можно интенсифицировать процесс фильтрования?
Лабораторная работа № 4
Изучение гидродинамики псевдоожиженного слоя.
1. Экспериментальное определение зависимости гидродинамического сопротивления слоя от фиктивной скорости воздуха, нахождение скорости псевдоожижения и скорости витания.
2. Аналитическое определение диаметра частиц, массы и порозности слоя.
При современном уровне производства ряд процессов химической технологии проводят при взаимодействии газов (или жидкостей) со слоем сыпучего материала (смешение, адсорбция, сушка, гранулирование, каталитические процессы и т.п.).
Если через неподвижный слой сыпучего материала, лежащего на пористой перегородке, пропускать снизу вверх поток газа (жидкости), то состояние слоя будет различным в зависимости от фиктивной скорости среды, под которой понимается ее расход, отнесенный к поперечному сечению аппарата. Различают четыре группы режимов взвешенного слоя в порядке возрастания скорости среды ( в дальнейшей воздуха):
I псевдоожижение (в том числе кипящий, виброкипящий, проходящий кипящий слой);
II фонтанирование (в т.ч, аэрофонтанный слой);
III пневмотранспорт ( вт.ч. восходящий, нисходящий, горизонтальный, «дюнами» и т.п.);
IV закрученные потоки (в т.ч. одиночные, встречные, спутные, вихревой слой и т.п.).
Псевдоожиженный (кипящий) слой получил свое название за внешнее сходство с поведением кипящей жидкости (он «течет», имеет пузыри, «кипит», принимает форму сосуда, в котором находится).
Процесс перевода сыпучего материала в «текучее» состояние называется псевдоожижением, а смесь сыпучего материала и ожижающего агента в состоянии полного псевдоожижения называется псевдоожиженнымслоем. На рис. I показаны различные стадии псевдоожиженияслоя по мере возрастания фиктивной скорости воздуха.
Скорость воздуха, при которой все частицы слоя переходят во взвешенное состояние, называется скоростью псевдоожижения w пс , или первой критической скоростью.
При дальнейшем увеличении скорости воздуха наступает такой момент, когда частицы материала начинают уноситься из аппарата (явление пневмотранспорта). Такая скорость воздуха называется скоростью уноса w ун , или второй критической скоростью. Интервал между двумя критическими скоростями, называется диапазоном существования псевдоожиженного слоя, а отношение любой скорости воздуха из этого интервала к скорости псевдоожижения называется числом псевдоожижения.
К основным характеристикам псевдоожиженного слоя относятся: перепад давления в слое ∆ P сл , скорость псевдоожижения w пс , скорость уноса (витания) w ун , , число псевдоожижения К= w раб / w пс и порозность слоя (как для неподвижного, так и для взвешенного слоя).
w ф1 > w ф2 > w ф3
а неподвижный слой; б псевдоожиженный слой; в пневмотранспорт.
Рисунок 1 Стадии псевдоожиженного слоя
а идеальная криваяпсевдоожижения б реальная кривая псевдоожижения
I Прямой ход; II Обратный ход.
Рисунок 2 Кривые псевдоожижения
Зависимость перепада давления в слое ∆Р сл от фиктивной скорости воздуха w ф называется кривой псевдоожижения.
На рис. 2а показана идеальная кривая псевдоожижения. Восходящая ветвь ОА соответствует режиму фильтрации воздуха через слой, при котором всё большая и большая доля частиц вовлекается в движение. Горизонтальный участок АВ изображает псевдоожиженное состояние, при котором все частицы слоя интенсивно перемешиваются. Постоянство перепада давления в слое объясняется равенством сил динамического воздействия потока среды на слой с одной стороны и силы тяжести за вычетом подъемной (архимедовой) силы с другой стороны:
Если средой является газ, то плотностью среды можно пренебречь, т.е. не учитывать подъемную силу:
Разделив обе части равенства (2) на площадь поперечного сечения аппарата S , получим условие равновесия слоя в состоянии псевдоожижения:
Т.е. потери давления в псевдоожиженном слое не зависят от скорости воздуха.
Теоретически гидродинамическое сопротивление псевдоожиженного слоя выражается зависимостью:
где: , Н 0 соответственно порозность и высота неподвижного слоя; =0,4.
Линия ВС (рис. 2а) характеризует уменьшение сопротивления слоя при массовом уносе частиц, так как уменьшается вес слоя G (см. формулу (3).
Критические скорости (первую и вторую) удобно определять по обобщенной зависимости Тодеса, справедливой для всех режимов движения воздуха в слое:
Подставляя в (5) значение порозности=0,4 или =1, получим зависимости для расчета соответственно первой и второй критических скоростей.
Порозностью (объемной долей пустот), называется отношение свободного объема между частицами к объему всего слоя:
где: V сл , V м объем слоя и материала соответственно, м 3 ;
, насыпная и кажущаяся плотность материала,кг/м 3
Из уравнения (5) можно найти теоретическое значение текущей порозностислоя:
На практике при неупорядоченной засыпке частиц неправильной формы величина порозности колеблется в пределах 0,35 — 0, 45.Для неподвижного слоя сферических монодисперстных частиц принимают =0,4, а при уносе частиц =1.
Промышленные сушилки устойчиво работают в интервалах порозности:
— сушилки кипящего слоя, = 0,55 0,75;
— аэрофонтанные сушилки, =0,75 0,9;
— трубы-сушилки, =0,9 0,95.
В отличие от описанной выше идеальной кривой псевдоожижения ОАВС, на рис. 2б представлена реальная кривая псевдоожижения для монодисперсного слоя, на которой четко виден пик перепада давления в слое. Характерно, что пик наблюдается только при возрастании скорости воздуха (прямой ход — кривая 1 на рис. 2б). При убывании скорости воздуха (обратный ход — кривая 2) пик исчезает. Если вновь увеличивать скорость воздуха, то пик также не наблюдается. Это объясняется тем, что плотность упаковки частиц в неподвижном слое до начала псевдоожижения несколько выше, чем в неподвижном слое после псевдоожижения. Поэтому при первоначальном увеличении скорости воздухадополнительные затраты энергии необходимы для преодоления сил инерции частиц, взаимного сцепления (когезии) частиц и трения их о стенки аппарата. При вторичном увеличении скорости воздуха эти силы незначительны. Величина пика давления зависит от свойств твердых частиц, геометрической формы аппарата и конструкции опорно распределительной решетки. В аппаратах постоянного поперечного сечения =(0,3 — 0,5)∙∆Р сл , в конических значительно больше.
Достоинствами псевдоожиженного слоя являются увеличения поверхности контакта фаз и их относительных скоростей движения, уменьшение внутри диффузного сопротивления твердой фазы в масообменных процессах. К недостаткам следует отнести снижение движущей силы процессов, обусловленное выравниванием полей температур и концентраций в слое; поршнеобразование, каналообразование, истирание твердых частиц и трудность равномерного распределения воздуха по сечению аппарата, особенно в аппаратах промышленного масштаба.
Описание экспериментальной установки
Установка для комплексного изучения параметров взвешенных слоев показана на рисунке 3. Она имеет общий вентилятор 1, аппарат кипящего слоя 2, аппарат фонтанирующего слоя 3 и циклон 4, снабженный сборником уловленного материала 5. Расход воздуха на псевдоожижение регулируется поворотным клапаном 6 и измеряется с помощью трубки Пито-Прандтля 8, подключенной к блоку U — образных манометров 10. Слой сыпучего материала находится на
газораспределительной решетке 11.
1 вентилятор; 2 аппарат кипящего слоя; 3 аппарат фонтанирующего слоя; 4 циклон; 5 сборник уловленного материала; 6,7 поворотные краны; 8,9 трубки Пито-Прандтля; 10 блок U -образных манометров; 11 газораспределительная решётка; 12,13 сетки; 14 мерная линейка
Рисунок 3 Схема экспериментальной установки
Методика выполнения работы
Сыпучий материал засыпается в аппарат кипящего слоя 2 сверху, замеряется высота неподвижного слоя Н 0 по линейке 14. Затем включается вентилятор 1 при полностью открытом кране 6. Снимаются 2-3 точки в режиме псевдоожижения, постепенно уменьшая расход воздуха краном 6, при этом перепад давления в слое остается постоянным. Важно найти точку, соответствующую переходу псевдоожиженного слоя в фильтрующий (уменьшается перепад давления в слое). В режиме фильтрации снимаются также 2-3 точки, уменьшая расход воздуха до нуля.
Для каждой точки измеряют следующие параметры: расход воздуха V в (трубки а-б на блоке манометров 10) с помощью тарировочного графика, размещенного на установке; перепад давления в слое ∆ P сл ( g -); высоту слоя Н сл
с помощью мерной линейки 14. Результаты измерений заносят в таблицу 1.
Таблица 1 Результаты измерений
Обработка результатов измерений
По данным таблицы 1 строится кривая псевдоожижения зависимость перепада давления в слое от фиктивной скорости воздуха:
w ф = v в /(0,785∙ D 2 ).
По кривой псевдоожижения определяются первая критическая скорость и соответствующий ей перепад давления в слое, по которому рассчитывается масса слоя М сл по формуле (3).
Из равенства (4) находится текущая порозность слоя , строится график зависимостии наносится на кривую псевдоожижения.
Используя график зависимости (рис.4), определяют средний диаметр частиц слоя d и вторую критическую скорость скорость уноса w ун . Для этого по скорости w пс рассчитывается критерий Лященко:
Затем при=0,4 находится соответствующее значение критерия Архимеда:
из которого определяется искомый диаметр. По данному значению Ar при =1 определяется другое критическое значение Ly ун , из которого находится искомая скорость w ун.
Расчетные значения заносятся в таблицу 2.
Таблица 2 Расчетные значения
Необходимые данные для расчета: D =0,147 м;ρ в =1,2 кг/м 3 ; ρ м =1280 кг/м 3 ; ν в =15,06∙10 -6 м 2 /с.
Рисунок 4 Зависимость
1.Что называется псевдоожижением?
2.Чем отличается псевдоожиженный слой от фильтрующего?
3.Что называется порозностью слоя?
4.Что называется кривой псевдоожижения?
5.Чем обусловлено наличие пика давления на реальной кривой псевдоожижения?
6.Почему кривая псевдоожижения снимается на обратном ходе?
7.Что такое число псевдоожижения?
8.Как зависит порозность от числа псевдоожижения?
9.Чем отличается скорость витания частиц от скорости уноса?
Лабораторная работа № 5
Изучение гидродинамики фонтанирующего слоя
- Экспериментальное определение зависимости перепада давления в слое от входной скорости воздуха.
- Нахождение критической скорости фонтанирования ω кр.ф. , скорости начала устойчивого фонтанирования ω н.у.ф. и скорости конца устойчивого фонтанирования ω к.у.ф. .
- Сравнение полученных скоростей с расчетными значениями.
По современным представлениям фонтанирующий слой, как и псевдоожиженный, является разновидностью взвешенного слоя. Однако, механизм движения газа и твердых частиц при фонтанировании существенно отличается от псевдоожижения. Классическое фонтарирование может быть осуществлено в цилиндрическом аппарате с коническим основанием, в центре которого имеется небольшое отверстие для подачи воздуха. При некоторой скорости воздуха струя прорывается через слой и образует на выходе так называемую шапку фонтана (рис. 1). В слое образуется ярко выраженное ядро фонтана (наиболее интенсивная зона аппарата) и периферийная зона .
Таким образом, отличительной особенностью фонтанирующего слоя является наличие нескольких зон, резко отличающихся между собой по характеру взаимодействия фаз. Наиболее полно структуру фонтанирующего слоя отображает трехзонная модель, подтвержденная экспериментально (рис. 1): ядро слоя 1, зона медленно движущихся частиц (пристенная зона 3), зона интенсивно движущихся частиц (опускная зона 4). Ядро имеет форму трубы Вентури с углом раствора конуса 8÷18˚. Позонную структуру фонтанирующего слоя можно наблюдать при переходе кипящего слоя к фонтанирующему, постепенно увеличивая угол раствора α конической части аппарата. При углах 0÷20˚ наблюдается типичное псевдоожижение в узких колонках подъем частиц в центре и вихреобразное опускание по стенкам. С увеличением угла раствора конуса до 40˚ ядро приобретает все более четкие очертания, а слой принимает трехзонную структуру. Обычно скорость воздуха в ядре на один два порядка выше, чем в пристеночной зоне, а объемная концентрация частиц в ядре меньше в 4 5 раз. В этих условиях интенсивность тепломассобмена в ядре в 1,5-2 раза выше, при этом максимум находится на границе ядра с опускной зоной.
Механизм перехода неподвижного слоя к фонтанирующему удобно описывать по кривым фонтанирования (псевдоожижения). На рис. 2 показана зависимости перепада давления ∆Р сл от скорости воздуха ω в нижнем сечении аппарата для фонтанирующего слоя (кривая 1) и для сравнения такая же зависимость для кипящего слоя (кривая 2) при одинаковой начальной высоте слоев Н 0 . На участке ОА слой неподвижен и сохраняет первоначальную структуру. Воздух фильтруется через слой. При дальнейшем увеличении расхода воздуха перепады давления слоя возрастает до максимального (точка В), а затем резко падает до точки С, которая называется точкой зарождения фонтана. Снижение давления до линии ВС отражает расширение плотного упакованного слоя. Дальнейшее увеличение скорости воздуха приводит к вытеснению и центрального ядра твердых частиц и прорыву газа через слой. Падение давления происходит очень резко до линии СД. Скорость воздуха, соответствующая давлению в точке Д, называется скоростью начала устойчивого фонтанирования ω н.у.ф. .За точкой Д перепад давления в слое почти постоянен, т.к. воздух беспрепятственно проходит через ядро слоя. Участок ДЕ характеризует режим развитого фонтанирования. За точкой Е начинается неустойчивый режим (поршнеобразование). Соответственно скорость газа в точке Е называется скоростью конца устойчивого фонтанирования ω к.у.ф. .
1 ядро; 2 шапка фонтана; 3 пристеночная зона; 4 опускная зона; 5 зеркало строя.
Рисунок 1 Структура фонтанирующего слоя
Отличительной особенностью кривой 1 является большой пик перепада давления слоя при выходе на режим фонтанирования ∆π ф . Он в 2-3 раза превышает рабочий перепад давления ∆Р ф , который в свою очередь меньше рабочего перепада для кипящего слоя: ∆Р ф =0,75∙∆Р к . Последнее объясняется тем, что концентрация твердых частиц в ядре фонтанирующего слоя меньше, чем в плотном кипящем слое при тех же средних скоростях воздуха. Как видно из рис. 2, небольшой пик давления имеет место также при обратном ходе (кривая 3) и связан с необходимостью затраты энергии на перестройку структуры слоя.
1 фонтанирующий слой; 2 кипящий слой; 3 обратный ход.
Рисунок 2 Кривые фонтанирования
По поводу природы пика давления ∆Р ф мнения различных авторов расходится. Зарубежные авторы считают, что появление пика кривой перепада давления как при фонтанировании, так и при псевдоожижении связано с затратой энергии, необходимой газовой струе для прорыва плотного слоя и оборудования “внутреннего канала” в нижней части слоя. Максимальный перепад давления (точка В) наблюдается при высоте внутреннего канала, 0,5∙Н 0 . Преобразуется ли в последствии этот внутренний канал в фонтан или произойдет переход к псевдоожижению, зависит от того, выполняются ли необходимые для фонтанирования условия по размеру частиц, диаметру отверстия, высоте слоя, углу раствора конуса и т.д. При дальнейшем увеличении высоты внутреннего канала до Н 0 перепад давления снижается до точки С, а когда струя прорывается на поверхность слоя падает до точки Д.
Некоторые советские авторы, изучавшие механизм потери устойчивости конического слоя на плоской (4-5 диаметров частиц слоя) двухмерной модели аппарата, утверждают, что сначала деформируется верхний слой частиц. Это происходит не во всем слое, а в осесиметричном центральном элементе его, имеющим форму перевернутого конуса с углом раствора 180 0 2α и диаметром основания Д в . После деформации нижнего слоя у входного отверстия “каверна” (пузырь), распространяющаяся вверх. Пик кривой фонтанирования (точка В) свидетельствует о деформации всех слоев, а прорыв “каверны” на поверхность слоя соответствует точке Д.
Фонтанирующий слой характеризуется 3-мя скоростями:
- критическая скорость фонтанирования ω кр.ф. , соответсвующие максимальному перепаду давления в слое ∆Р max ;
- скорость начала устойчивого фонтанирования ω н.у.ф , при которой наступает хорошее перемешивание слоя;
- скорость конца устойчивого фонтанирования ω к.у.ф , пр повышении которой начинается поршнеобразование.
Критическая скорость фонтанирования зависит от высоты слоя, физических характеристик частиц и воздуха, а также от геометрических характеристик установки:
где: D 0 диаметр верхнего сечения слоя, м:
Скорость начала устойчивого фонтанирования может быть определена из соотношения :
На скорость конца устойчивого фонтанирования ω к.у.ф также оказывает влияние высота аппарата Н апп. И диаметр сепарационного пространства D сеп :
Зависимости (1) (3) справедливы в диапазоне 20 Re вит
Отношение максимального перепада давления к перепаду при устойчивом фонтанировании зависит от геометрии аппарата и физических свойств воздуха и частиц:
Зависимость (4) справедлива в диапазоне 4,4 ∙10 3 Ar 6
Фонтанирующий слой имеет целый ряд преимуществ перед кипящим: большая интенсивность процесса, более упорядоченная циркуляция материала, отсутствие газораспределительной решетки, возможность обработки полидисперсных материалов.
К недостаткам фонтанирующего слоя относятся сравнительно низкая интенсивность процесса тепломассообмена в пристеночной зоне, большой пик перепада давления слоя при выходе на режим фонтанирования и истирания материала.
В связи с этим основными направлениями интенсификации аппаратов фонтанирующего слоя является активизация пристеночной зоны, снижение пускового пика перепада давления и повышения кратности циркуляции частиц в слое.
На рис. 3 показаны некоторые конструкции аппаратов с модифицированным фонтанирующим слоем. Основной идеей, заложенной в эти конструкции, является активизация пристеночной зоны, являющейся наименее активной в аппарате боковые хордальные вводы, расположенные на конусной части аппарата (рис 3а), существенно изменяет гидродинамическую структуру потоков в аппарате, ускоряя циркуляцию частиц из периферийной зоны в ядро.
а) с хордальными вводами; б) с вращающимся слоем материала; в) с искусственно сформированным ядром и встречными струями; г) с тангенциальными щелевыми соплами.
I ожижающий агент; II исходный материал; III распыливающий агент; I У готовый продукт; У воздух на сепарацию частиц; У I высокотемпературный агент; У II газовзвесь.
Рисунок 3 Схемы аппаратов с модифицированным фонтанирующим слоем
Аппарат с вращающимся слоем материала (рис. 3б) по структуре потоковой твердой фазы близок к аппарату идеального вытеснения, т.к. рецикл материала отсутствует.В аппарате, показанном на рис.3в, во взвешенном слое установлена трубчатая вставка, которая служит для искусственного формирования ядра и снижения пускового пика перепада давления, но главное ее назначение регулирование времени цикла циркуляции τ ц твердой фазы в аппарате.
Аппарат с пирамидальным днищем и щелевыми соплами, показаный на рис.3г, служит для обработки дисперсных материалов повышенной истираемостью и адгезионными свойствами. За счет ввода щелевых сопел объем центрального ядра увеличен, что приводит к интенсификации процесса тепломассообмена в таком аппарате.
Соотношение потоков æ: 1 0; 2 0,33; 3 0,6; 4 0,66; 5 0,73.
Рисунок 4 Кривые фонтанирования
Для аппаратов с боковыми вводами теплоносителя, показаных на рис. 3, кривые фонтанирования имеют спецефическую особенность, обусловленную соотношением суммарного бокового и общего потока воздуха æ = ∑ L бок / L общ (см. рис.4).С ростом соотношения потоков происходит снижение пика перепада давления ∆Р max и уменьшением ω н.у.ф, но в тоже время происходит некоторое увеличение перепада давления ∆Р ф . Последнее обстоятельство объясняется увеличением подвижности частиц в пристроечной зоне, что приводит к увеличению массы материала, находящегося в состоянии фонтанирования (т.е. в ядре слоя).
Как видно из рисунка 4, оптимальными являются соотношения потоков æ =0,66-0,73 (кривые 4,5) при которых пик перепада давления минимален, а рабочий перепад давления ∆Р ф примерно равен начальному перепаду давления ∆Р 0 , обусловленному только наличием боковых потоков. На основании последнего можно сделать важный вывод, что при оптимальном соотношении потоков æ массы частиц, находящихся во вращающемся слое и в состоянии фонтанирования, должны быть одинаковы.
Описание экспериментальной установки
Схема установки приведена на рис. 3 в предыдущей работе №4. Воздух на фонтанирование подается вентилятором 1, при этом кран 6 закрывается, а кран 7 открывается. Расход воздуха измеряется с помощью трубки Пито-Прандтля 9 и блока манометров 10. Сетки 12,13 служат соответственно для удержания материала в аппарате при нерабочем состоянии и для предотвращения уноса материала из аппарата.
Методика выполнения работы
В аппарат фонтанирующего слоя 3 засыпается сыпучий материал и измеряется начальная высота слоя Н 0 . Вентилятор 1 выключается при полностью закрытых кранах 6,7. Затем медленно открывают кран 7 и снимают 2-3 точки в режиме фильтрации. Один из студентов неотрывно следит за показаниями манометров 10, стараясь заметить максимальную разность уровней жидкости в трубках Л-М. Очень важно не упустить этот момент т.к. в противном случае придется начинать все сначала. В режиме устойчивого фонтанирования также снимаются 2-3 точки , увеличивая расход воздуха до тех пор, пока не начнется поршнеобразование в слое.
Для каждой точки измеряют: расход воздуха V в (трубки В-Г) с помощью тарировочного графика, размещенного на установке; перепад давления в слое ∆Р сл. (л-м). Результаты измерений заносят в таблицу 1.
Обработка результатов измерений
Вначале рассчитывается скорость воздуха ω, м/с в патрубке:
Строится кривая фонтанирования , по которой определяются все искомые скорости. По формулам (1) (3) аналитически рассчитываются те же скорости и сравниваются с экспериментально найденными, оценивается относительная погрешность по формуле:
По формуле (4) рассчитывается соотношение и сравнивается с экспериментальным. Оценивается погрешность по формуле, аналогичной (6).
Для расчета необходимо использовать справочные данные по скоростям витания для различных материалов, либо воспользоваться результатами лабораторной работы № по изучению скорости витания сыпучих материалов. Результаты заносятся в таблицу 2.
Таблица 2 Результаты эксперимента и расчетов
🎬 Видео
Сравнение разных типов мешалок при перемешивании вязкой среды.Скачать

Выборка: расчет объема. Достоверность и мощность исследования. Биостатистика.Скачать

Обзор на верхнеприводные погружные мешалки 5drops #shortsСкачать

Мешалка верхнеприводнаяСкачать

3 модели верхнеприводных мешалок 5DropsСкачать

Расчет статически неопределимой стержневой системы. Уравнение совместимости деформацийСкачать

Быстроходная мешалка 1Скачать

Монтаж промышленной мешалки VJ500 на емкостьСкачать

Программное обеспечение для расчета надёжности молниезащиты любого объекта за 30 минутСкачать

Мешалка для еврокуба Мешалка для емкости Промышленное перемешивание составовСкачать

Расчет элементов железобетонных конструкций по деформациям.Скачать
Мешалки водоочистительных системСкачать

Новое поколение верхнеприводных мешалок EUROSTARSСкачать

Расчет рым-болта Методом конечных элементовСкачать

Пример сильно-связанного термомеханического расчета для моделирования процесса горячей прокаткиСкачать

Видео работы лопастной мешалки со складными лопастямиСкачать

Расчет абсолютной погрешностиСкачать


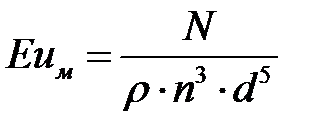 .
.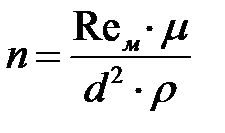 .
.






















