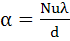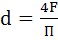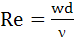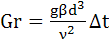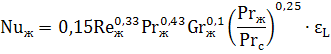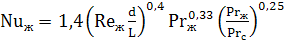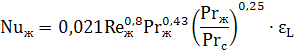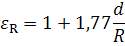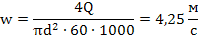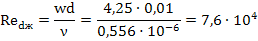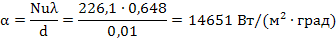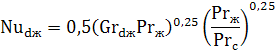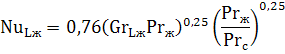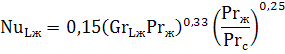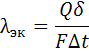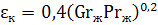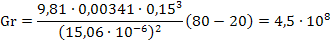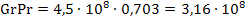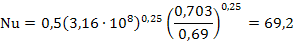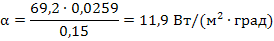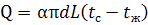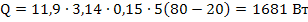Критериальное уравнение для естественной конвекции

Используя теорию подобия из системы дифференциальных уравнений 10.4, 10.9, 10.10 и 10.11 можно получить уравнение теплоотдачи (10.3) для конвективного теплообмена в случае отсутствия внутренних источников тепла в следующем критериальной форме:

где: X₀; Y₀; Z₀ – безразмерные координаты;
Nu = α ·l₀/λ — критерий Нуссельта (безразмерный коэффициент теплоотдачи), характеризует теплообмен между поверхностью стенки и жидкостью (газом);
Re = w·l₀/ν — критерий Рейнольдса, характеризует соотношение сил инерции и вязкости и определяет характер течения жидкости (газа);
Gr = (β·g·l₀ 3 ·Δt)/ν 2 — критерий Грасгофа, характеризует подьемную силу, возникающую в жидкости (газе) вследствие разности плотностей;
Pr = ν/а = (μ·c_p)/λ — критерий Прандтля, характеризует физические свойства жидкости (газа);
l₀ – определяющий размер (длина, высота, диаметр).

Расчетные формулы конвективного теплообмена.

Приведем некоторые основные расчетные формулы конвективного теплообмена (академика М.А.Михеева), которые даны для средних значений коэффициентов теплоотдачи по поверхности стенки.

1. Свободная конвекция в неограниченном пространстве.

а). Горизонтальная труба диаметром d при 10 3 8 .

б). Вертикальная труба и пластина:
1). ламинарное течение — 10 3 9 :

Здесь значения Gr_жd и Pr _ж берутся при температуре жидкости (газа), а Pr_ст при температуре поверхности стенки.
Для воздуха Pr _ж/Pr_ст = 1 и формулы (10.13-10.15) упрощаются.
2. Вынужденная конвекция.
Режим течения определяется по величине Re.
а). Течение жидкости в гладких трубах круглого сечения.
1). ламинарное течение – Re 0,33 ·Pr_ж 0,33 ·(Gr_жd·Pr_ж) 0,1 ·(Pr_ж/Pr_ст) 0,25 ·ε_l , (10.16)

где ε_l — коэффициент, учитывающий изменение среднего коэффициента теплоотдачи по длине трубы и зависит от отношения длины трубы к его диаметру (l/d). Значения этого коэффициента представлена в таблице 10.1.
Таблица 10.1.
Значение ε_l при ламинарном режиме.

Коэффициент К₀ зависит от критерия Рейнольдса Re и представлена в таблице 10.2.
Таблица 10.2.
Значение К₀ .

3). турбулентное течение – Re = 10 4

Таблица 10.3.
Значение ε_l при турбулентном режиме.

б).Обтекание горизонтальной поверхности.
1). ламинарное течение – Re 4

в). Поперечное обтекание одиночной трубы (угол атаки j = 90 0 ).
1). при Re_жd = 5 — 10 3

Тема 11. Тепловое излучение.

Видео:Л2 - Конвективный теплообмен.Скачать

Критериальные уравнения теплообмена: расчет теплоотдачи в трубах и каналах

Видео:Подобие процессов конвективного теплообменаСкачать

Теплоотдача при вынужденном течении жидкости в трубах и каналах

Теплоотдача в трубах и каналах может происходить при вынужденном или свободном характере конвекционных потоков (возможны также их сочетания в случае существенного влияния гравитационных сил).

При вынужденном течении (вынужденная конвекция) жидкость нагнетается или отводится под действием сил внешнего давления, например, ветра, насоса или вентилятора.

Свободное течение жидкости происходит под действием подъемных (гравитационных) сил за счет изменения ее плотности из-за разницы температуры – слой жидкости с меньшей плотностью стремиться занять верхнее положение относительно холодного слоя (свободная или естественная конвекция).

Интенсивность теплоотдачи, как при вынужденной, так и при свободной конвекции характеризуется коэффициентом теплоотдачи α, имеющим размерность Вт/(м 2 ·град), который определяется по формуле:

Nu – число Нуссельта; λ – коэффициент теплопроводности жидкости при средней температуре, Вт/(м·град);

d – эквивалентный диаметр, равный

F – площадь сечения канала, м 2 ; П – периметр канала, м.

Для трубы круглого сечения, эквивалентный диаметр равен внутреннему диаметру трубы.

В целом, расчет коэффициента теплоотдачи сводится к определению числа Нуссельта, значение которого задается соответствующими критериальными уравнениями конвективного теплообмена, зависящими от режима течения жидкости и формы канала.

Течение жидкости в трубах определяется значением числа Рейнольдса Re и в зависимости от его величины может быть ламинарным, переходным или турбулентным.

• Ламинарный режим течения жидкости характеризуется величиной числа Re до 2300.
• При значении числа Re от 2300 до 10000 режим течения в трубах является переходным.
• Турбулентный режим течения в трубах наблюдается при числах Re более 10000.

Число (критерий) Рейнольдса представляет собой безразмерный комплекс, связывающий скоростные и вязкостные характеристики жидкости с определяющим размером канала (для трубы – это ее диаметр).

Число Re определяется по формуле:

w – скорость течения жидкости, м/с; d – эквивалентный диаметр канала, м; ν — кинематическая вязкость жидкости при средней температуре, м 2 /с.

Теплоотдача в трубах и каналах существенно зависит от режима течения жидкости. При ламинарном режиме интенсивность теплоотдачи значительно меньше, чем при развитом турбулентном.

Теплоотдача при ламинарном течении в трубах и каналах

Ламинарный режим течения жидкости обычно характеризуется низкой скоростью потока. При этом в некоторых случаях влиянием конвекции, обусловленной действием гравитационных сил, пренебрегать нельзя.

Для выбора правильного критериального уравнения теплообмена и оценки влияния естественной конвекции на интенсивность теплопередачи при ламинарном режиме служит критерий Грасгофа Gr.

g – ускорение свободного падения, м/с 2 ;

β – температурный коэффициент объемного расширения, град -1 ;

d – эквивалентный диаметр канала, м;

ν — кинематическая вязкость жидкости при средней температуре, м 2 /с;

Δt – средняя разность температур жидкости и стенки, °С.

Теплоотдача при ламинарном течении в трубах и каналах с учетом естественной конвекции. Если величина комплекса GrPr превышает 8·10 5 , то расчет коэффициента теплоотдачи необходимо проводить с учетом влияния естественной конвекции в потоке жидкости по следующему критериальному уравнению:

Индекс «ж» означает, что свойства среды, входящие в критерии подобия Re, Pr и Gr берутся при средней температуре жидкости.

Число Прандтля с индексом «с» Pr_с берется для жидкости при температуре стенки.

ε_L – коэффициент, учитывающий изменение теплоотдачи по длине трубы или канала. Его можно определить с помощью таблицы:

Теплоотдача при ламинарном течении в трубах и каналах без учета естественной конвекции. При значении GrPr 5 , влияние естественной конвекции на теплоотдачу жидкости пренебрежительно мало, и расчет коэффициента теплоотдачи можно проводить по следующему критериальному уравнению:

d – эквивалентный диаметр канала, м;

L – длина трубы (канала), м.

Представленные критериальные уравнения теплообмена при ламинарном режиме позволяют определить среднее значение числа Нуссельта, по величине которого можно рассчитать средний коэффициент теплоотдачи:

λ – коэффициент теплопроводности жидкости при средней температуре, Вт/(м·град);

d – эквивалентный диаметр, м.

Теплоотдача в трубах и каналах при турбулентном режиме

Теплоотдача в трубах и каналах при турбулентном режиме осуществляется путем передачи тепла при интенсивном перемешивании слоев жидкости. Критериальное уравнение теплообмена для расчета средней теплоотдачи в трубах и каналах в этом случае имеет вид:

Критерии подобия Re и Pr берутся при средней температуре жидкости. Число Прандтля с индексом «с» Pr_с берется при температуре стенки.

Представленное критериальное уравнение применяется в диапазоне чисел Re от 1·10 4 до 5·10 6 и Pr от 0,6 до 2500.

ε_L – коэффициент, учитывающий изменение среднего коэффициента теплоотдачи по длине трубы или канала при турбулентном режиме течения. Значения ε_L приведены в следующей таблице при различных числах Рейнольдса и отношениях длины канала к его эквивалентному диаметру:

Расчет теплоотдачи в изогнутых трубах и каналах проводится по тому же критериальному уравнению с добавлением множителя — поправки на действие центробежных сил, которая определяется по формуле:

R — радиус изгиба трубы или канала, м; d – эквивалентный диаметр трубы или канала, м.

Теплоотдача в изогнутых трубах проходит более интенсивно, чем в прямых, за счет большего вихреобразования и лучшего перемешивания жидкости.

Расчет теплоотдачи при вынужденной конвекции

Пример расчета. Рассчитаем средний коэффициент теплоотдачи воды, текущей по трубопроводу длиной 1 м, диаметром d=0,01 м с расходом Q=20 л/мин. Средняя температура воды t_ж=50°С, температура стенки трубы t_с=10°С.

1. Определим физические свойства воды при температуре 50°С:

• Теплопроводность воды λ_ж= 0,648 Вт/(м·град);
• Плотность воды ρ_ж=988 кг/м 3 ;
• Кинематическая вязкость воды ν_ж=0,556·10 -6 , м 2 /с;
• Число Прандтля при температуре жидкости Pr_ж=3,54;
• Число Прандтля при температуре стенки Pr_с=9,52.

2. Рассчитаем среднюю скорость течения воды w по трубе:

3. Определим число Рейнольдса Re:

4. Поскольку число Рейнольдса имеет значение больше 1·10 4 , то режим течения является турбулентным и расчет теплоотдачи необходимо проводить по следующему критериальному уравнению:

Определим коэффициент ε_L по соотношению L/d=1/0,01=100. Поскольку L/d>50, то коэффициент ε_L=1_.

Выполним расчет числа Нуссельта по приведенному критериальному уравнению:

5. Рассчитаем средний коэффициент теплоотдачи от воды к стенке трубы по формуле:

Таким образом, средний коэффициент теплоотдачи от воды к стенке трубы составляет 14,65 кВт/(м 2 ·град).

Видео:Основы конвективного теплообменаСкачать

Теплоотдача при свободной конвекции в трубах и каналах

Теплообмен при свободном движении жидкости (или газа) происходит вследствие разности плотностей нагретых и холодных ее слоев. Интенсивность теплоотдачи жидкости в трубах и каналах при свободной конвекции существенно зависит от их положения в пространстве относительно силы тяжести.

Теплоотдача при свободной конвекции имеет различный характер в случаях свободного течения в неограниченном пространстве и теплообмена в ограниченном объеме (в узкой трубе или канале).

Свободная конвекция в неограниченном пространстве

Конвекция в неограниченном пространстве протекает, например при охлаждении трубопровода центрального отопления, расположенного на улице в безветренную погоду, вблизи от которого отсутствуют препятствия для движения воздушных потоков.

Горизонтальный канал или труба. Интенсивность теплоотдачи при свободной конвекции зависит от величины комплекса GrPr. При значении GrPr от 10 3 до 10 9 критериальное уравнение, описывающее среднюю теплоотдачу от поверхности горизонтальных труб и каналов, имеет вид:

В качестве определяющего размера принимается наружный диаметр d канала или трубы.

Вертикальный канал (труба, пластина). Для вертикальных труб и каналов при значении GrPr от 10 3 до 10 9 критериальное уравнение, описывающее среднюю теплоотдачу, имеет вид:

При GrPr>10 9 :

Примечание: В приведенных критериальных уравнениях теплообмена свойства жидкости, входящие в числа Gr и Pr, определяются при температуре окружающей среды. Число Прандтля с индексом «с» Pr_с берется для жидкости при температуре стенки. В качестве определяющего размера принимается длина L (высота) вертикально стоящей трубы или канала.

Свободная конвекция в ограниченном объеме

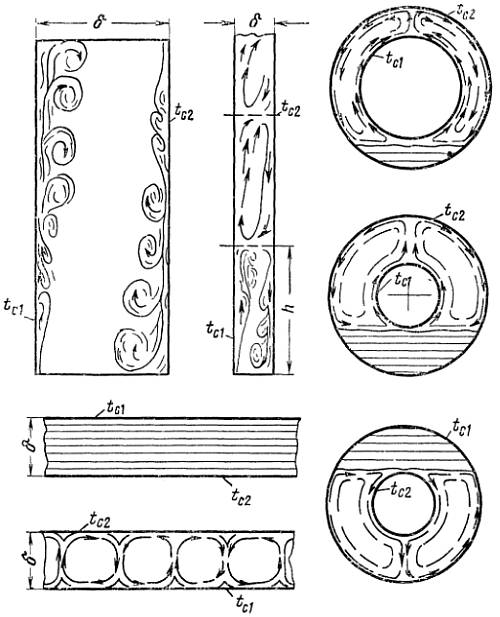
Теплообмен жидкости в ограниченном объеме при свободной конвекции характеризуется совместным протеканием процессов нагрева и охлаждения соседних слоев жидкости (или газа). Эти процессы сопровождаются сложным течением нисходящих и восходящих потоков, зависящих от рода жидкости, разницы температуры, формы канала и его геометрических размеров.

Для упрощения расчета таких сложных процессов конвективного теплообмена принято рассматривать их, как явление теплопроводности в щели толщиной δ с учетом понятия эквивалентного коэффициента теплопроводности λ_эк.

Эквивалентный коэффициент теплопроводности определяется по формуле:

Q — количество переданного тепла, Вт; δ — толщина слоя жидкости (или газа), м; F — площадь теплоотдающей поверхности, м 2 ; Δt=t_c1-t_c2 — температурный напор между нагретой и холодной стенками, °С.

Отношение эквивалентного коэффициента теплопроводности λ_эк к величине теплопроводности окружающей жидкости при средней температуре называется коэффициентом конвекции ε_к, который определяется значением комплекса GrPr.

При малых значениях комплекса GrPr 3 6 :

При 10 6 10 :

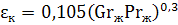
Примечание: Числа подобия Gr и Pr рассчитываются при средней температуре жидкости (или газа), равной t_ж=0,5(t_c1+t_c2). В качестве определяющего размера принимается δ — толщина слоя жидкости.

Расчет теплоотдачи при свободной конвекции

Пример расчета. Рассчитаем потери тепла естественной конвекцией от горизонтального трубопровода центрального отопления, находящегося на открытом воздухе. Диаметр трубопровода d=0,15 м, длина L=5 м, средняя температура наружной стенки t_с=80°С. Температура окружающего воздуха t_ж=20°С.

1. Определим физические свойства воздуха при температуре 20°С:

• Теплопроводность воздуха λ_ж= 0,0259 Вт/(м·град);
• Кинематическая вязкость воздуха ν_ж=15,06·10 -6 , м 2 /с;
• Число Прандтля при температуре жидкости Pr_ж=0,703;
• Число Прандтля при температуре стенки Pr_с=0,69;
• Коэффициент объемного расширения β_ж=1/(273+20)=0,00341 град -1 .

2. Вычислим число Грасгофа Gr по формуле:

3. Определим значение комплекса GrPr:

Этому значению комплекса соответствует следующее критериальное уравнение теплообмена при свободной конвекции в случае горизонтальной трубы:

4. Вычислим значение числа Нуссельта Nu:

5. Рассчитаем коэффициент теплоотдачи от трубы α по формуле:

6. Определим потери тепла с боковой поверхности трубопровода по формуле:

Подставляя численные значения, окончательно получаем потерю тепла:

Таким образом, только путем естественной (свободной) конвекции рассмотренный трубопровод отопления отдает воздуху 1681 Вт тепла.

Видео:Физика 8 класс (Урок№2 - Теплопроводность, конвекция, излучение)Скачать

Реферат: Конвективный теплообмен 2

Закон Ньютона – Рихмана.

Краткие сведения из теории подобия.

Критериальные уравнения конвективного теплообмена.

Расчетные формулы конвективного теплообмена.

Теория теплообмена изучает процессы распространения теплоты в твердых, жидких и газообразных телах. Перенос теплоты может передаваться тремя способами:

• теплопроводностью;
• конвекцией;
• излучением (радиацией).

Процесс передачи теплоты теплопроводностью происходит при непосредственном контакте тел или частицами тел с различными температурами и представляет собой молекулярный процесс передачи теплоты. При нагревании тела, кинетическая энергия его молекул возрастает и частицы более нагретой части тела, сталкиваясь с соседними молекулами, сообщают им часть своей кинетической энергии.

Конвекция – это перенос теплоты при перемещении и перемешивании всей массы неравномерно нагретых жидкости или газа. При этом, перенос теплоты зависит от скорости движения жидкости или газа прямо пропорционально. Этот вид передачи теплоты сопровождается всегда теплопроводностью. Одновременный перенос теплоты конвекцией и теплопроводностью называется конвективным теплообменом.

В инженерных расчетах часто определяют конвективный теплообмен между потоками жидкости или газа и поверхностью твердого тела. Этот процесс конвективного теплообмена называют конвективной теплоотдачей или просто теплоотдачей.

Процесс передачи теплоты внутренней энергии тела в виде электромагнитных волн называется излучением (радиацией). Этот процесс происходит в три стадии: превращение части внутренней энергии одного из тел в энергию электромагнитных волн, распространение э/м волн в пространстве, поглощение энергии излучения другим телом. Совместный теплообмен излучением и теплопроводностью называют радиационно-кондуктивным теплообменом.

Совокупность всех трех видов теплообмена называется сложным теплообменом.

Процессы теплообмена могут происходит в различных средах: чистых веществах и разных смесях, при изменении и без изменения агрегатного состояния рабочих сред и т.д. В зависимости от этого теплообмен протекает по разному и описывается различными уравнениями.

Процесс переноса теплоты может сопровождаться переносом вещества (массообмен). Например испарение воды в воздух, движение жидкостей или газов в трубопроводах и.т.п. и.т.д. Тогда процесс теплообмена усложняется, так как теплота дополнительно переносится с массой движущегося вещества.

Процесс теплообмена между поверхностью тела и средой описывается законом Ньютона – Рихмана, которая гласит, что количество теплоты, передаваемая конвективным теплообменом прямо пропорционально разности температур поверхности тела (t_‘ст )и окружающей среды (t_‘ж ):

где: коэффициент теплоотдачи [Вт/(м 2 К)], характеризует интенсивность теплообмена между поверхностью тела и окружающей средой.

Факторы, которые влияют на процесс конвективного теплообмена, включают в этот коэффициент теплоотдачи. Тогда коэффициент теплоотдачи является функцией этих параметров и можно записать эту зависимость в виде следующего уравнения:

где: Х – характер движения среды (свободная, вынужденная);

Ф – форма поверхности;

l_o – характерный размер поверхности (длина, высота, диаметр и т.д.);

w_o – скорость среды (жидкость, газ);

θ = (t_‘ст — t_‘ж ) – температурный напор;

λ – коэффициент теплопроводности среды;

а – коэффициент температуропроводности среды;

с_р –изобарная удельная теплоемкость среды;

ρ –плотность среды;

ν – коэффициент кинематической вязкости среды;

β – температурный коэффициент объемного расширения среды.

Уравнение (3) показывает, что коэффициент теплоотдачи величина сложная и для её определения невозможно дать общую формулу. Поэтому для определения коэффициента теплоотдачи применяют экспериментальный метод исследования.

Достоинством экспериментального метода является: достоверность получаемых результатов; основное внимание можно сосредоточить на изучении величин, представляющих наибольший практический интерес.
Основным недостатком этого метода является, что результаты данного эксперимента не могут быть использованы, применительно к другому явлению, которое в деталях отличается от изученного. Поэтому выводы, сделанные на основании анализа результатов данного экспериментального исследования, не допускают распространения их на другие явления.

Следовательно, при экспериментальном методе исследования каждый конкретный случай должен служить самостоятельным объектом изучения.

Краткие сведения из теории подобия.

При исследовании конвективного теплообмена применяют метод теории подобия .

Теория подобия – это наука о подобных явлениях. Подобными явлениями называются такие физические явления, которые одинаковы качественно по форме и по содержанию, т.е. имеют одну физическую природу, развиваются под действием одинаковых сил и описываются одинаковыми по форме дифференциальными уравнениями и краевыми условиями.
Обязательным условием подобия физических явлений должно быть геометрическое подобие систем, где эти явления протекают. Два физических явления будут подобны лишь в том случае, если будут подобны все величины, которые характеризуют их.

Для всех подобных систем существуют безразмерные комплексы величин, которые называются критериями подобия .

Основные положения теории подобия формулируют в виде 3-х теорем подобия.

1 теорема: Подобные явления имеют одинаковые критерии подобия.

2 теорема: Любая зависимость между переменными, характеризующая какие-либо явления, может быть представлена, в форме зависимости между критериями подобия, составленными из этих переменных, которая будет называться критериальным уравнением .

3 теорема: Два явления подобны, если они имеют подобные условия однозначности и численно одинаковые определяющие критерии подобия.
Условиями однозначности являются:

наличие геометрического подобия систем;

наличие одинаковых дифференциальных уравнений;

существование единственного решения уравнения пр заданных граничных условиях;

известны численные значения коэффициентов и физических параметров.

Используя теорию подобия из системы дифференциальных уравнений, можно получить уравнение теплоотдачи (3) для конвективного теплообмена в случае отсутствия внутренних источников тепла в следующем критериальной форме :

где: X₀ ; Y₀ ; Z₀ – безразмерные координаты;

Nu = α ·l₀ /λ — критерий Нуссельта (безразмерный коэффициент теплоотдачи), характеризует теплообмен между поверхностью стенки и жидкостью (газом);

Re = w·l₀ /ν — критерий Рейнольдса , характеризует соотношение сил инерции и вязкости и определяет характер течения жидкости (газа);

Gr = (β·g·l₀ 3 ·Δt)/ν 2 — критерий Грасгофа , характеризует подьемную силу, возникающую в жидкости (газе) вследствие разности плотностей;

Pr = ν/а = (μ·c_p )/λ — критерий Прандтля , характеризует физические свойства жидкости (газа);

l₀ – определяющий размер (длина, высота, диаметр).

Приведем некоторые основные расчетные формулы конвективного теплообмена (академика М.А.Михеева), которые даны для средних значений коэффициентов теплоотдачи по поверхности стенки.

1. Свободная конвекция в неограниченном пространстве.

а) Горизонтальная труба диаметром d при 10 3 8 .

б) Вертикальная труба и пластина:

ламинарное течение — 10 3 9 :

Здесь значения Gr_жd и Pr _ж берутся при температуре жидкости (газа), а Pr_ст при температуре поверхности стенки.

Для воздуха Pr _ж /Pr_ст = 1 и формулы (5-7) упрощаются.

Режим течения определяется по величине Re.

а) Течение жидкости в гладких трубах круглого сечения.
ламинарное течение – Re 0,33 ·Pr_ж 0,33 ·(Gr_жd ·Pr_ж ) 0,1 ·(Pr_ж /Pr_ст ) 0,25 ·ε_l , (8)

где ε_l — коэффициент, учитывающий изменение среднего коэффициента теплоотдачи по длине трубы и зависит от отношения длины трубы к его диаметру (l/d). Значения этого коэффициента представлена в таблице 1.

Таблица 1. Значение ε_l при ламинарном режиме.

переходной режим – 2100 4

Коэффициент К₀ зависит от критерия Рейнольдса Re и представлена в таблице 2.

турбулентное течение – Re = 10 4

Таблица 3. Значение ε_l при турбулентном режиме.

б) Обтекание горизонтальной поверхности.

ламинарное течение – Re 4

в)Поперечное обтекание одиночной трубы (угол атаки j = 90 0 ).
при Re_жd = 5 — 10 3

Основными факторами, влияющими на процесс теплоотдачи являются следующие:

1). Природа возникновения движения жидкости вдоль поверхности стенки.

Самопроизвольное движение жидкости (газа) в поле тяжести, обусловленное разностью плотностей её горячих и холодных слоев, называют свободным движением (естественная конвекция) .

Движение, создаваемое вследствие разности давлений, которые создаются насосом, вентилятором и другими устройствами, называется вынужденным (вынужденная конвекция) .

2). Режим движения жидкости.

Упорядоченное, слоистое, спокойное, без пульсаций движение называется ламинарным .

Беспорядочное, хаотическое, вихревое движение называется турбулентным .

3). Физические свойства жидкостей и газов.

Большое влияние на конвективный теплообмен оказывают следующие физические параметры: коэффициент теплопроводности (l), удельная теплоемкость (с), плотность (ρ), κоэффициент температуропроводности (а = λ/c_р ·ρ), коэффициент динамической вязкости (μ) или кинематической вязкости (ν = μ/ρ), температурный коэффициент объемного расширения (β = 1/Т).

4). Форма (плоская, цилиндрическая), размеры и положение поверхности (горизонтальная, вертикальная).

1. Лариков Н.Н. Теплотехника: Учебник для вузов. -3-е изд., перераб. и дополн.-М.; Стройиздат, 1985 -432 с.ил.

2. Нащокин В.В. Техническая термодинамика и теплопередача. -М.; Высшая школа, 1969 -560с.

3. Михеев М.А., Михеева И.М. Основы теплопередачи. -М.; Энергия, 1977.

4. Теплотехника /Хазен М.М., Матвеев Г.А. и др. -М.; 1981.

5. Панкратов Г.П. Сборник задач по теплотехнике. М.; Высш. шк., 1986. -248с.

🔥 Видео

КонвекцияСкачать

Интуитивное понимание формулы теплопроводности (часть 11) | Термодинамика | ФизикаСкачать

КонвекцияСкачать

Физика. «Конвекция»Скачать

Основы теории теплообменаСкачать

Теплопроводность, конвекция, излучение. 8 класс.Скачать

Теплопередача. Виды теплопередачи | Физика 8 класс #2 | ИнфоурокСкачать

Учебный фильм - ТеплообменСкачать

Теплопроводность | Теплопередача, конвекция, излучениеСкачать

8 класс урок №4 Теплопроводность Конвекция ИзлучениеСкачать

Лекция 1.4 Оcновы теории подобия. Критериальные параметры.Скачать

Решение уравнения теплопроводности методом конечных разностейСкачать

Урок 106 (осн). Виды теплопередачи (часть 1)Скачать

§5. Физика 8 кл. Конвекция.Скачать

Методы исследования технологических процессов. Теория подобия. Виды подобияСкачать

Теплопроводность, конвекция и тепловое излучение (часть 8) | Термодинамика | ФизикаСкачать