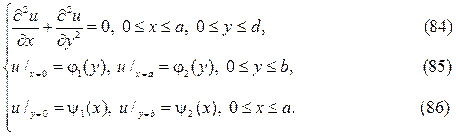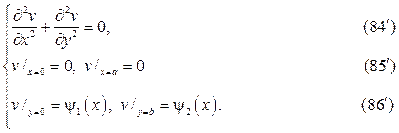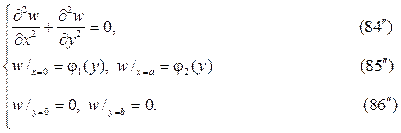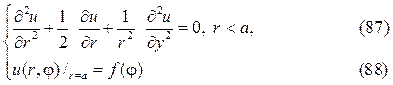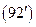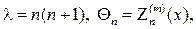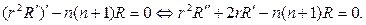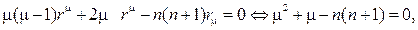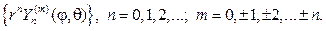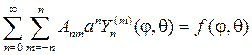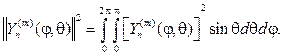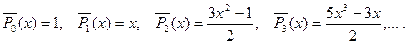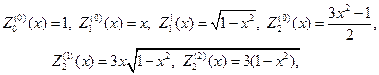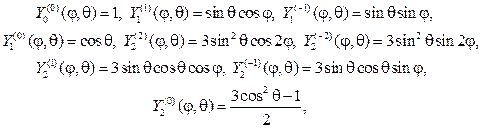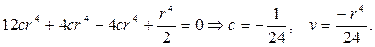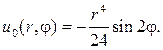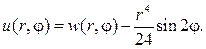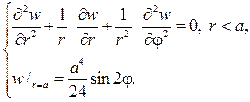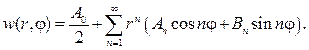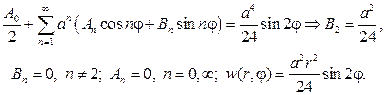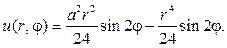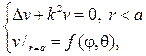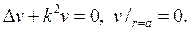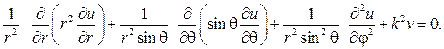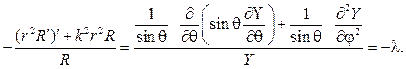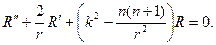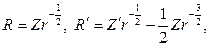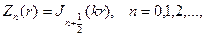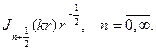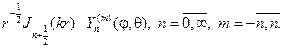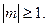ЭЛЛИПТИЧЕСКОГО ТИПА
Краевые задачи для уравнения Лапласа в прямоугольнике (полупо- лосе), решаются методом разделения переменных в декартовых коорди- натах, в круговой областях (круг, сектор, кольцо) методом разделения пе- ременных в полярных координатах. При решении краевых задач для ци-линдрических и сферических областей используются соответственно ци- линдрические и сферические координаты бесселевы функции, полиномы и присоединённые функции Лежандра, а также шаровые функции. Возни- кающие здесь задачи Штурма 
Лиувилля своеобразны, их граничные ус- ловия определяются спецификой областей:
следует искать в виде суммы u(x,y)=v(x,y)+w(x,y),где v(x,y) и w(x,y) гар- монические функции в том же самом треугольнике, точнее они суть ре-шения краевых задач
Штрихованные краевые задачи решаются методом разделения пере- менных в терминах тригонометрических и гиперболических функций.
Рассмотрим задачу Дирихле для круга
где f(j)кусочно-непрерывная функция.
Следуя схеме метода Фурье полагаем
подставляем в (87) и разделяем переменные. В результате получим ра -венство
(90)
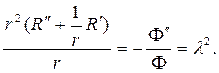
Угловая функция F(j) обязана быть периодической с периодом 2p. Присоединяя условие периодичности к дифференциальному уравнению для F(j), найдем задачу Штурма Лиувилля
откуда следует, что
(91)
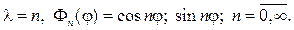
Возвращаясь к (80), решаем уравнение для радианальной функции. При
r 2 R² + rR¢ n 2 R = 0,
решение следует искать в виде степенной функции R=r m . Для определе- ния m получим соотношение
m(m 1)r m +m r m 
n 2 r m =0Û m 2 
n 2 =0,
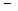
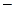
Если же n=0, то уравнение, как нетрудно проверить, rR² + R¢ =0имеет своими решениями функции
R0(r) = 1; lnr. 
С учетом (89) мы должны составить произведения угловых и радиаль- ных функций и получить набор функций, гармонических в круге
Если предположить, что ряд
(93)
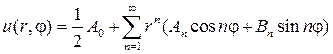
можно дифференцировать почленно дважды по r и j , то его сумма также будет гармонической функцией, т. е. будет решением уравнения (87). Подставляя (93) в (88), найдем
(94)
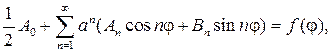
откуда с учетом формул коэффициентов Фурье следует
(95)
(96) Итог состоит в том, что решение задачи (87 88) дается рядом (93), коэффициенты которого определены равенствами (95-96).
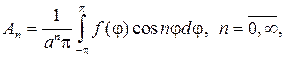
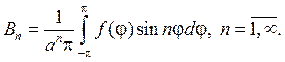
Замечание 1. Мы можем говорить, очевидно, что ряд (93) дает общий вид гармонической функции для круга r — n и lnr, поскольку они разрывны в
центре круга r=0.
Напротив, если рассматривать область r>a, то нельзя привлекать r — n и lnr, и общий вид гармонической функции для внешности круга будет да- ваться рядом
(97)
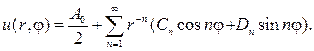
В случае кругового кольца a 2 q= 1-x 2 , найдем
(104¢)
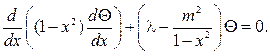
Соответственно и граничные условия (105) перейдут после замены в неравенства
(105′)
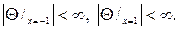
Задача (104¢) (105¢) есть известная задача для присоединенных функций Лежандра, ее решение (см., например, [3], стр. 115)
и возвращаясь к переменной q, найдем собственные значения и собствен- ные функции задачи (104), (105):
(106)
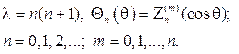
Составив произведения функций (106) на найденные выше функции Fm(j), получим множество решений уравнения (102)
(107)
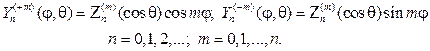
Эти решения принято называть сферическими функциями, их основ-ное свойство в приводимой ниже теореме.
Теорема 1. Сферические функции взаимно ортогональны на единич- ной сфере, т.е. при m1¹m2 или n1¹n2
(108)
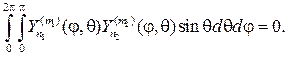
Теперь возвращаясь к равенству (101), возьмем уравнение для ради- альной функции
Оно имеет решение в виде степенной функции R=r m . Действительно, после подстановки
откуда находим значения m=n; (n+1) и соответственно решения
(109)
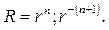
Умножая первые из функций (109) на сферические функции (107), получаем множество частных решений уравнения Лапласа в шаре:
Согласно схеме метода Фурье. составляем ряд с произвольными коэффи- циентами
(110)
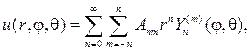
который будет гармонической функцией в шаре, если только его можно дифференцировать почленно.
Для нахождения коэффициентов Аnm подставим (110) в (100), тогда
и с учетом (108) найдем
(111)
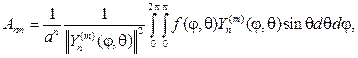
Последний интеграл вычисляется и при m=0 :
(112)
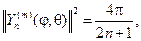
если же |m| ³ 1, то имеем
(113)
Завершая рассмотрение задачи (99),(100), скажем, что мы нашли ее решение в виде ряда (110), коэффициенты которого определяются в согласии с (111),(113).
Замечание 3. Напомним, что нормированные полиномы Лежандра вы- числяяются по формулам
(114)
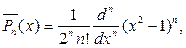
В свою очередь присоединенные функции Лежандра выражаются че- рез производные от полиномов Лежандра, т. е.
(115)
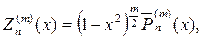
в частности будем иметь
(116)
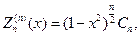
где Сn определенная константа.
С учетом (107), (115) и (116) выпишем несколько сферических функций:
(117)
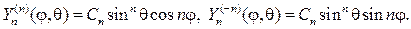
Замечание 4. При решении краевых задач для внешности шара вместо соотношения (110) нужно использовать ряд
(118)
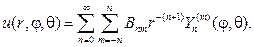
Общий вид гармонической функции в шаровом слое a 4 , и получим
Таким образом, частным решением будет функция
Вводим новую неизвестную функцию w(r,j) , полагая
Тогда относительно w(r,j) нужно решать задачу Дирихле для урав- нения Лапласа
Согласно (93), решение этой задачи дается формулой
Подставляя ее в граничное условие, получим
Ответом в задаче будет функция
254. Найдите решение первой краевой задачи для уравнения Гельмгольца
предполагая, что k не является собственным значением задачи
Р е ш е н и е. Запишем уравнение в сферических координатах
Беря u(r,j,q,)=R(r)Y(j,q), после разделения переменных придем к дифференциальным уравнениям:
Функция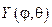 
будет решением уравнения (72), которое нужно решать при условии ограниченности и 2p-периодичности по j. В результате при- дем к сферическим функциям при l=n(n+1):
Относительно радиальной функции R(r) нужно решать дифференци- альное уравнение
Выполняя в этом уравнении замену
придем к соотношению относительно новой функции Z(r):
Последнее уравнение в качестве ограниченных в окрестности нуля
r=0 решений имеет бесселевы функции
соответственно будем иметь набор радиальных функций
Умножая их на сферические функции, получим набор решений урав- нения Гельмгольца:
Составляем ряд с числовыми коэффициентами
(119)
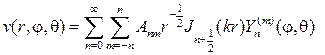
и определяем коэффициенты так, чтобы выполнялась граничное условие при r=a
где d = 4 при m = 0 и d =2 при 
При найденных коэффициентах Anm ряд (119) будет решением рассматриваемой краевой задачи для уравнения Гельмгольца.
255. Найдите такую гармоническую u(r,j,q) функцию внутри шарового слоя 1
Видео:6.2 Решение задач для уравнения Лапласа в круге, вне круга и в кольцеСкачать
Краевая задача для уравнения лапласа в шаре
Настоящая книга является естественным дополнением пособия А. Г. Свешникова, А. Н. Боголюбова, В. В. Кравцова «Лекции по математической физике». Её основная цель помочь студентам приобрести необходимые практические навыки исследования математических моделей физических явлений, являющихся краевыми или начально-краевыми задачами для линейных дифференциальных уравнений в частных производных второго порядка. С этой целью каждая глава пособия построена следующим образом. В начале каждого параграфа главы приводятся необходимые минимальные сведения теоретического характера, используемые для решения данного типа задач. Затем эти методы демонстрируются в работе, для чего даются примеры решения конкретных задач. В конце главы приводятся задачи с ответами для самостоятельного решения.
Содержание пособия полностью соответствует курсу «Методы математической физики», читаемому на физическом факультете МГУ. Пособие написано на основе более чем двадцатилетнего опыта преподавания на физическом факультете Московского университета. Оно рассчитано в первую очередь на студентов физических специальностей университетов, но будет полезно и студентам инженерных специальностей и лицам, занимающимся математической физикой и прикладной математикой.
Авторы выражают свою глубокую благодарность заведующему кафедрой Московского государственного института электронной профессору А. С. Поспелову, профессорам А. В. Ефимову, А. С. Ильинскому и С. Я. Секерж-Зеньковичу, взявшим на себя труд ознакомиться с рукописью и сделавшим ряд ценных замечаний.
Видео:Решение уравнения Лапласа в шареСкачать
Боковая панель
Полное и подробное, насколько это возможно, решение уравнения Лапласа в сферических координатах, приводящее к шаровым и сферическим функциям. Всё самое интересное на, хоть и длинной, но одной странице. Много математики — много веселья!
Эту запись можно посмотреть в nbviewer.
Видео:Задача Дирихле для круга. Уравнение ЛапласаСкачать
Уравнение Лапласа в сферических координатах
Уравнение Лапласа в сферических координатах имеет вид
где $ r, vartheta = 90^circ — varphi, lambda $ — радиус, полярное расстояние (дополнение широты $varphi$ до $90^circ$), долгота соответственно.
Решить уравнение Лапласа это значит найти конкретный вид гармонической функции $f left( r, vartheta, lambda right)$, удовлетворяющей ему.
Прежде, чем переходить к решению, заметим важное и полезное свойство уравнения Лапласа: оно линейно. Это означает, что если есть два решения этого уравнения $f_1$ и $f_2$, то есть
$$ Delta f_1 = 0,qquad Delta f_2 = 0, $$
то их линейная комбинация
$$ f = alpha f_1 + beta f_2 $$
тоже является решением $Delta f = 0$.
Видео:6.1 Уравнение Лапласа в полярных координатах. Принцип решения и постановка задачСкачать
Разделение переменных
Будем искать решение уравнения Лапласа методом разделения переменных, суть которого в следующем. Представим искомую функцию $f$ трёх переменных $r, vartheta, lambda$ как произведение трёх других функций
begin f left(r, vartheta, lambda right) = R(r) cdot Theta left( vartheta right) cdot Lambda left( lambda right), end
каждая из которых теперь зависит только от одной переменной: $R$ есть функция только от $r$, $Theta$ есть функция только от $vartheta$, а $Lambda$ есть функция только от $lambda$. Стоит заметить, что не всякая система координат позволяет решить уравнение Лапласа методом разделения переменных, например этого нельзя сделать в геодезических координатах $H, B, L$.
Итак, делаем подстановку
Замечаем, что частные производные заменены на полные дифференциалы, поскольку функции $R, Theta, Lambda$ имеют только одну переменную. Разделим обе части уравнения на $RThetaLambda$ и умножим на $r^2$:
Первый член уравнения зависит только от $r$, а вся оставшаяся часть зависит только от угловых величин $vartheta, lambda$. Для того, чтобы равенство выполнялось необходимо, чтобы обе части равнялись некоторой постоянной $alpha$:
Первое уравнение будем называть радиальной частью уравнения Лапласа, поскольку она зависит только от $r$. Оставшуюся часть умножим на $sin^$ и запишем уравнение
которое является угловой частью уравнения Лапласа и называется дифференциальным уравнением сферических функций, поскольку, как увидим позже, именно они будут его решением.
И снова становится очевидным, что для сохранения равенства в полученном уравнении необходимо, чтобы обе части равнялись некоторой постоянной $beta$:
Таким образом, уравнение Лапласа, дифференциальное уравнение в частных производных второго порядка, разбивается на три обыкновенных дифференциальных уравнения второго порядка:
$$ begin r^2 frac <d^R><d r^> + 2 r frac — alpha R &= 0, label tag\ frac frac <d^Theta><d vartheta^> + frac< tan> frac- alpha Theta sin^- dfrac<sin> &= 0, label tag \ frac<d^Lambda><d lambda^> + beta Lambda &= 0. label tag end $$ Нам требуется теперь решить каждое из уравнений в отдельности, а заодно и определить вид постоянных $alpha$ и $beta$.
Отметим, что угловая часть уравнения Лапласа $Y (vartheta, lambda) = Theta (vartheta) Lambda (lambda)$ зависит только от полярного расстояния $vartheta$ и долготы $lambda$, то есть явялется функцией, заданной на сфере, следовательно решение этой части должно быть периодическим: $pi$ для широтной части и $2pi$ для долготной части. Только при этих условиях функция $Y (vartheta, lambda)$ может быть однозначно заданной на сфере.
Видео:Краевая задача для уравнений Лапласа и Пуассона на R^2Скачать
Уравнение гармонических колебаний
Обыкновенное дифференциальное уравнение второго порядка вида
называется уравнением гармонических (или свободных) колебаний.
Оно имеет два линейно независимых решения при $beta > 0$
что легко проверяется подстановкой.
Как уже было сказано выше, для того, чтобы функция $Y left( vartheta, lambda right)$ была однозначной на сфере, необходимо, чтобы функция $Lambda$ имела период $2pi$. Из последнего уравнения нетрудно установить, что такое возможно только при $beta = m^2$, $m = 0, 1, 2, …$ Таким образом, решения уравнения гармонических колебаний принимают вид
линейная комбинация которых
является общим решением дифференциального уравнения. Здесь $C_1$ и $C_2$ — произвольные константы.
Видео:Задача Дирихле для шараСкачать
Присоединённое уравнение Лежандра
Перепишем второе уравнение, подставив в него значение $beta = m^2$:
И подставляя всё это, получим уравнение без тригонометрических функций в явном виде:
$$ left( 1 — t^2 right) dfrac
Сначала установим некоторые свойства решения этого уравнения.
- Во-первых, поскольку $t = cos$, то $-1 leq t leq +1$. Таким образом, областью определения $P (t)$ является интервал $[-1, 1]$.
- Во-вторых, поскольку $0 leq vartheta leq pi$ и $-1 leq t leq +1$, то по теорема Вейерштрасса функция $P (t)$ является ограниченной и должна принимать некоторые конечные значения на этом интервале:
$$ left|P (-1)right| Сферические функции
Пользуясь полученными нами решениями уравнения гармонических колебаний и присоединённого уравнения Лежандра, мы можем записать теперь решение дифференциального уравнения для сферических функций (или угловой части уравнения Лапласа) в виде:
$$ Y_n^m left( vartheta, lambda right) = P_n^m (cos) cos ,qquad Y_n^m left( vartheta, lambda right) = P_n^m (cos) sin ,qquad $$
Функции такого вида называют элементарными сферическими функциями степени $n$ и порядка $m$. Видно, что степень и порядок элементарной сферической функции определяется степенью и порядком присоединённой функции Лежандра.
Поскольку дифференциальное уравнение для сферических функций является линейным, то и линейная комбинация его решений также будет решением. Эту комбинацию можно записать как
где $A_n^m$ и $B_n^m$ являются произвольными константами, которые ещё называют гармоническими коэффициентами или просто гармониками. Мы получили общее выражение для сферической функции степени $n$.
Видео:Часть 1. Примеры на краевую задачу Лапласа в кругеСкачать
Уравнение Коши-Эйлера
Наконец, найдём решение радиальной части уравнения Лапласа. Запишем её снова:
begin r^2 frac + 2 rfrac — alpha R = 0. end
Это уравнение Коши—Эйлера — линейное дифференциальное уравнение второго порядка с переменными коэффициентами. Будем искать решение в виде степенной функции $R = r^n$, тогда
Подставляем в дифференциальное уравнение и после тривиальных преобразований, получаем
begin n(n — 1) r^n + 2nr^n — alpha r^n = 0. end
Сокращаем на $r^n$, получаем характеристическое уравнение
begin n^2 + n — alpha = 0, end
два корня которого легко находим из решения квадратного уравнения
откуда, возвращаясь к нашей подстановке $R = r^n$, получаем два линейно независимых решения
Теперь, пользуясь значением для $alpha = n (n + 1)$, которое мы установили выше при рассмотрении присоединённого уравнения Лежандра, находим решения
линейная комбинация которых
по свойству линейных ОДУ второго порядка, является общим решением дифференциального уравнения. Здесь $C_1, C_2$ — произвольные постоянные.
Таким образом, мы получили решение радиальной (зависимой только от $r$) части уравнения Лапласа.
Видео:7.2 Уравнение Лапласа в секторе и кольцевом сектореСкачать
Шаровые функции
Итак, мы решили все обыкновенные дифференциальные уравнения, возникшие после разделения переменных в уравнении Лапласа в сферических координатах. Осталось найти окончательный вид решения. Напоминаю, что искали мы его в виде
begin f left(r, vartheta, lambda right) = R(r) cdot Theta left( vartheta right) cdot Lambda left( lambda right) = R(r) cdot Y left( vartheta, lambda right). end
Подставляем сюда выражения eqref для $R$ и получаем два решения вида
begin f left(r, vartheta, lambda right) = r^ Y (vartheta, lambda),quad f left(r, vartheta, lambda right) = r^ Y (vartheta, lambda), end
которые называются шаровыми функциями (solid spherical harmonics), а функции $Y (vartheta, lambda)$ — сферическими (spherical harmonics). Таким образом, последние два выражения устанавливают связь шаровых и сферических функций.
Используя общее выражение для сферической функции степени $n$ eqref, шаровые функции можно записать так
begin f left(r, vartheta, lambda right) &= r^ sumlimits_^n (A_n^m cos + B_n^m sin) P_n^m (cos),\ f left(r, vartheta, lambda right) &= dfrac<r^> sumlimits_^n (A_n^m cos + B_n^m sin) P_n^m (cos). end
Вспоминая свойство линейности, о котором мы упоминали в самом начале, можно записать общее решение уравнения Лапласа, как линейную комбинацию частных решений в виде ряда по степеням $n$:
begin f left(r, vartheta, lambda right) &= sumlimits_^ r^ sumlimits_^n (A_n^m cos + B_n^m sin) P_n^m (cos),\ f left(r, vartheta, lambda right) &= sumlimits_^ dfrac<r^> sumlimits_^n (A_n^m cos + B_n^m sin) P_n^m (cos). end
Эти выражения называются рядами шаровых функций, а при $r = 1$ они обратятся в ряды сферических функций или ряды Лапласа.
Ряды шаровых функций и являются решением уравнения Лапласа в сферических координатах.
Для геодезии, изучающей внешнее гравитационное поле, куда более важными являются шаровые функции вида $f = r^ Y_n (vartheta, lambda)$, через которые может быть выражен потенциал притяжения вне притягивающих масс, поскольку $r$ здесь, как и у потенциала притяжения стоит в знаменателе. Вообще говоря, любая гармоническая вне сферы функция $f_e$ ($e$, external) может быть разложена в ряд
$$ f_e = sumlimits_^ r^ Y_n (vartheta, lambda) $$,
а любая гармоническая внутри сферы функция $f_i$ ($i$, internal) может быть разложена в ряд
$$ f_i = sumlimits_^ r^n Y_n (vartheta, lambda).$$
🎬 Видео
7.2 Задача 1. Краевая задача для уравнения ПуассонаСкачать
OTAROVA JAMILA МЕТОД ФУРЬЕ РЕШЕНИЯ ЗАДАЧИ ДИРИХЛЕ ДЛЯ УРАВНЕНИЯ ЛАПЛАСА В КРУГЕСкачать
7.1 Решение уравнения Лапласа в прямоугольникеСкачать
7.6 Задача 5. Краевая задача для уравнения ПуассонаСкачать
Краевая задача для уравнений Лапласа и Пуассона на R^2Скачать
УМФ, 24.11, уравнение Лапласа в кругеСкачать
Уравнение Лапласа. Задача Дирихле для уравнения Лапласа внутри и вне кругаСкачать
Дифференциальные уравнения | задача Штурма - Лиувилля | классические краевые задачи | 1Скачать
Уравнения математической физики 15+16 Задача Дирихле для уравнения Лапласа - Пуассона в кругеСкачать
Оператор Лапласа в полярных координатахСкачать
Задача Неймана для уравнения Лапласа. Третья краевая задача для уравнения ЛапласаСкачать
