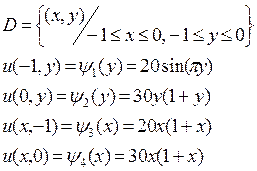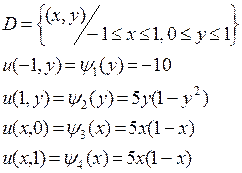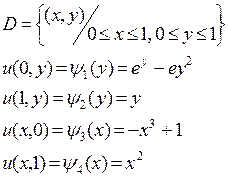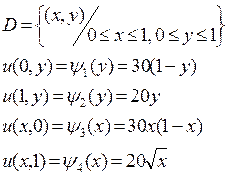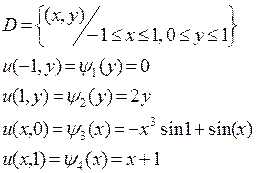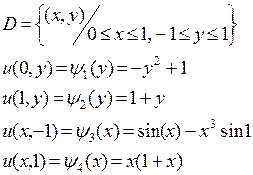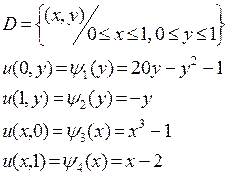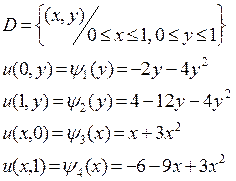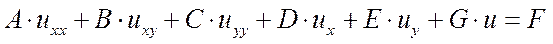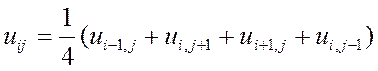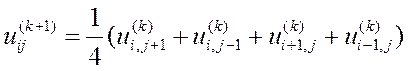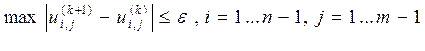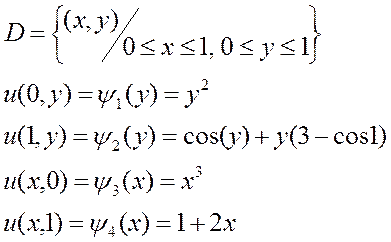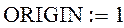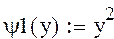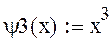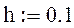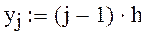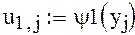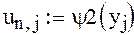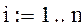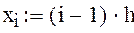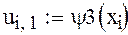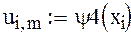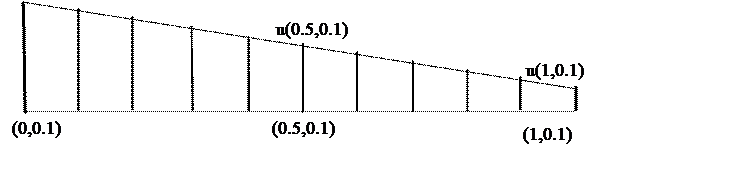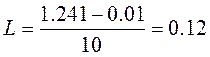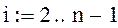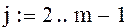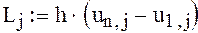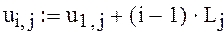1. Краткая теория
уравнение функция лаплас программа
В настоящей лабораторной работе методом сеток требуется решить задачу Дирихле для уравнения Лапласа. Эта задача ставится следующим образом.
Найти непрерывную функцию и (х, у), удовлетворяющую внутри прямоугольной области уравнению Лапласа
и принимающую на границе области заданные значения, т. е.




Будем считать, что и(х, у) непрерывна на границе области , т. е. , , , . Выбрав шаги h, l по x и y соответственно, строим сетку , , , , где , .
Вводя обозначения , аппроксимируем частные производные и в каждом внутреннем узле сетки центральными разностными производными второго порядка
и заменим уравнение Лапласа конечно-разностным уравнением
Погрешность замены дифференциального уравнения разностным составляет величину .
Уравнения (1) вместе со значениями в граничных узлах образуют систему линейных алгебраических уравнений относительно приближенных значений функции и (х, у) в узлах сетки . Наиболее простой вид имеет эта система при :


При получении сеточных уравнений (2) была использована схема узлов, изображенная на рис. 1. Набор узлов, используемых для аппроксимации уравнения в точке, называется шаблоном. В данной работе используется шаблон типа «крест».
Численное решение задачи Дирихле для уравнения Лапласа в прямоугольнике состоит в нахождении приближенных значений искомой функции и(х, у) во внутренних узлах сетки. Для определения величин требуется решить систему линейных алгебраических уравнений (2).
В данной лабораторной работе она решается методом Гаусса—Зейделя, который состоит в построении последовательности итераций вида
(верхним индексом s обозначен номер итерации). При последовательность сходится к точному решению системы (2). В качестве условия окончания итерационного процесса можно принять
Таким образом, погрешность приближенного решения, полученного методом сеток, складывается из двух погрешностей: погрешности аппроксимации дифференциального уравнения разностными; погрешности, возникающей в результате приближенного решения системы разностных уравнений (2).
Известно, что описанная здесь разностная схема обладает свойством устойчивости и сходимости. Устойчивость схемы означает, что малые изменения в начальных данных приводят к малым изменениям решения разностной задачи. Только такие схемы имеет смысл применять в реальных вычислениях. Сходимость схемы означает, что при стремлении шага сетки к нулю () решение разностной задачи стремится в некотором смысле к решению исходной задачи. Таким образом, выбрав достаточно малый шаг h, можно как угодно точно решить исходную задачу.
Видео:7.1 Решение уравнения Лапласа в прямоугольникеСкачать

Основные понятия метода сеток. Задача Дирихле для уравнения Лапласа
Метод сеток (или метод конечных разностей) сводит решение систем уравнений в частных производных к решению систем линейных, как правило, алгебраических уравнений с достаточно разреженными матрицами. При этом построение решения в методе сеток осуществляется в три этапа.
- • Область непрерывного изменения аргумента (или аргументов) заменяется конечным дискретным множеством точек, называемых разностной сеткой. В разностной сетке выделяются внутренние и граничные узлы. Решение ищется во внутренних узлах, а в граничных узлах значение искомой функции задается при аппроксимации граничных условий исходной дифференциальной задачи. Функция дискретного аргумента, определенная на разностной сетке, называется СЕТОЧНОЙ ФУНКЦИЕЙ.
- • Дифференциальное уравнение и граничные условия заменяются по определенным правилам своими разностными аналогами. Разностные операторы, соответствующие дифференциальному уравнению, записываются во внутренних узлах сетки. Разностные операторы, соответствующие граничным условиям, записываются в граничных узлах. В результате получается система алгебраических уравнений, число которых пропорционально числу внутренних узлов разностной сетки.
- • Осуществляется решение системы алгебраических уравнений каким-либо из известных методов. В большинстве случаев получаемая система уравнений есть система линейных алгебраических уравнений достаточно большого порядка, но с весьма разреженной матрицей. В случае нелинейных систем итерационные процедуры, как правило, сводят их к линейным системам.
Основные понятия и этапы метода сеток продемонстрируем на примере решения задачи Дирихле для классического уравнения эллиптического типа — уравнения Лапласа. Итак, имеем уравнение Лапласа
и граничное условие
где Г — граница области G (рис. 4.4), в которой ищется решение и(х, у), удовлетворяющее уравнению (4.7) и граничному условию (4.8).
На первом этапе метода сеток область G непрерывного изменения аргумента с границей Г заменяют приближающей ее сеточной областью Gh с границей Г’А. Для этого проведем линии
при п = 0, . N. Величины hx и h , называемые шагами разностной сетки, в общем случае могут быть различными.
Рис. 4.4 Рис. 4.5
Точки пересечения линий х = const и у = const называют УЗЛАМИ РАЗНОСТНОЙ СЕТКИ. Различают два типа узлов — ВНУТРЕННИЕ и ВНЕШНИЕ. Внутренними называют такие узлы, для которых четыре соседних узла (по два в каждом направлении) принадлежат области G = G + Г. Сеточной функции приписываются нижние индексы. На рис. 4.4 внутренние узлы обозначены пустыми кружочками, а граничные — залитыми.
На втором этапе заменим дифференциальный оператор Лапласа разностным оператором. С этой целью выберем шаблон разностной схемы — набор (конфигурацию) узлов, с использованием которых производится замена производных конечными разностями. Шаблон, содержащий р точек, называется р-точечным. Для аппроксимации вторых производных, входящих в оператор Лапласа, применим пятиточечный шаблон, показанный на рис. 4.5. Не теряя общности рассуждений, рассмотрим далее случай, когда шаги разностной сетки по направлению х иу одинаковы, т. е. hx — hy = h. С использованием разложения функции на точном решении в ряд Тейлора в окрестности точки (*, у) имеем
Из этих соотношений получим аппроксимации вторых производных со вторым порядком точности
Введем для сокращения записи общепринятые индексные обозначения узлов в соответствии с рис. 4.5 и соответствующие обозначения сеточных функций в узлах: ит ит. „ и т. д. Тогда соотношения для производных примут вид
При этом разностный оператор Лапласа Дuh на пятиточечном шаблоне может быть выписан как
Аппроксимация граничных условий осуществляется с помощью различных приемов. Для случая прямоугольной области с границами, совпадающими с линиями х — const и у — const, граничные значения известны в узлах точно, так как и0 h = = uQ(mhx, nhy). Для области произвольной формы значения сеточной функции в граничных узлах принимаются равными значениям функции и0 в ближайших (по какому-либо критерию) точках кривой Г (рис. 4.4). Для задачи Неймана или смешанной задачи, когда на границе области задается значение производной функции и, производится аппроксимация производной.
Записав разностный оператор (4.11) во всех внутренних узлах, получим систему сеточных уравнений для нахождения значений сеточной функции ит п в узлах разностной сетки.
На третьем этапе осуществляется решение системы сеточных уравнений. В общем случае сеточные уравнения могут быть нелинейными. Однако в рассматриваемой задаче, в силу линейности основного дифференциального уравнения Лапласа, система уравнений (4.11) является системой линейных алгебраических уравнений для нахождения значений неизвестных во внутренних узлах. При этом число уравнений системы точно равно числу внутренних узлов разностной сетки. Отметим, что число уравнений может быть весьма велико. Так, для нахождения достаточно точного решения рассматриваемой задачи требуется задать числа N = М порядка 50—100, и, следовательно, количество уравнений достигает нескольких сотен или даже тысяч.
Перепишем систему сеточных решений в виде
Отметим, что каждое из уравнений системы содержит лишь пять неизвестных ит , . „, и„ , „ . ,, ит „ ., и„ хотя в полной
системе таких неизвестных содержится порядка N 2 . Таким обра- зом, матрица системы (4.12) является сильно разреженной. Системы с такими матрицами хорошо решаются с помощью итерационных методов: простой итерации, Зейделя, релаксационных. Рассмотрим их применение к решению системы (4.12).
Запишем систему (4.12) в виде
Значение функции в центральной точке есть среднее арифметическое значений функции в четырех соседних по направлениям х и у узлах. Уравнение (4.13) можно интерпретировать как разностный аналог теоремы о среднем для гармонических функций.
Рассмотрим применение метода простой итерации для решения системы (4.13). Для простоты предположим, что область G имеет прямоугольную форму (рис. 4.6). Построим итерационный процесс
Здесь верхний индекс означает номер итерации. В граничных точках значения известны точно. Для нахождения решения по соотношению (4.14) необходимо знать начальное приближение — значения функции на нулевой итерации ц ( ®* п. Можно доказать, что для любого шага разностной сетки итерационный процесс (4.14) сходится независимо от начального приближения и п. На практике желательно выбирать начальное приближение возможно более близким к точному решению. Например, на основании теоремы о среднем для гармонических функций в качестве хорошего начального приближения можно принять значение функции, полученное интерполяцией на область G значений
функции в граничных узлах. Так, значение функции и (0) в центральной точке 1 (рис. 4.6) может быть взято как среднее арифметическое значений функции в граничных узлах a, b, с, d.
Сходимость итерационного процесса можно улучшить, если использовать итерационный процесс Зейделя в виде, например,
Члены с индексами (т — 1, п) и (т, п — 1) берутся из k-й итерации, т. е. в вычислениях используются уточненные значения функции в этих точках. Как легко понять из рис. 4.6, расчет по формуле (4.15) при движении, например, слева направо от границы области позволяет последовательно вычислить значения функции на слоях у = const (или х = const). Использование уточненных значений функции улучшает сходимость метода итераций и позволяет уменьшить требуемый для реализации метода объем оперативной памяти компьютера, так как в методе Зейделя не требуется одновременно хранить значение функции в каждой точке на двух итерациях. Итерации заканчиваются при выполнении условия max |u^ — ” **1 1 итерационный метод называется методом ВЕРХНЕЙ РЕЛАКСАЦИИ, при со = 1 — методом ПОЛНОЙ РЕЛАКСАЦИИ и при со 2 ]пе-‘
Метод итераций Зейделя
Метод верхней релаксации
Видно, что в методе верхней релаксации число итераций для достижения заданной точности линейно зависит от числа узлов N, тогда как в остальных методах зависимость квадратичная.
Видео:Задача Дирихле для круга. Уравнение ЛапласаСкачать

Решение задачи Дирихле для уравнения Лапласа методом сеток
Страницы работы
Фрагмент текста работы
12. РЕШЕНИЕ ЗАДАЧИ ДИРИХЛЕ ДЛЯ УРАВНЕНИЯ ЛАПЛАСА
12.1. Цель работы
Целью работы является закрепление знаний, полученных в лекционном курсе «Вычислительная математика» по разделу «Численные методы решения дифференциальных уравнений в частных производных», приобретение навыков использования соответствующих численных методов с применением программных средств автоматизации вычислений.
Найти приближенное решение уравнения Лапласа в заданной области с указанными граничными условиями, принять h1=h2=0.1
1.
2.
3.
4.
5.
6.
7.
8.
12.3 Теоретические сведения
Уравнение относительно неизвестной функции u(x,y) двух или более независимых переменных , которое содержит частные производные этой функции, называется уравнением в частных производных (УЧП).
В общем виде ДУ второго порядка относительно функции двух независимых переменных u(x,y) записывается так :
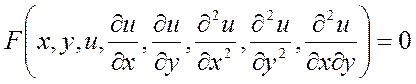
Функция F— заданная функция восьми аргументов .
Далее будем рассматривать линейные уравнения второго порядка :
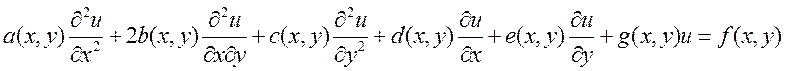
Методы классификации УЧП :
· По порядку уравнения ( наивысший порядок частных производных, входящих в уравнение)
· По числу переменных ( по числу независимых переменных )
· По критерию « линейное-нелинейное»
A,B,C,D,E,F,G – константы или заданные функции переменных x,y.
· По критерию «однородное-неоднородное»
Однородное , если G(x,y)≡0 для всех x и y.
Если G(x,y)≠0 – неоднородное .
· По виду коэффициентов
A,B,C,D,E,F,G – константы – уравнение с постоянными коэффициентами.
Основные типы УЧП :
Описывает процессы теплопроводности и диффузии : B 2 =4AC
Описывает колебательные системы и волновые движения : B 2 >4AC
Описывает установившиеся процессы : B 2 2 ).
Для уравнения Лапласа система может быть записана в виде:
В данной работе система решается методом простых итераций по формулам:
В качестве условия окончания итерационного процесса можно принять:
Данная разностная схема обладает свойством устойчивости и сходимости. Это означает , что выбрав достаточно малый шаг h можно сколь угодно точно численно решить исходную задачу.
12.4 Пример выполнения задания
Найти решение задачи Дирихле для уравнения Лапласа :
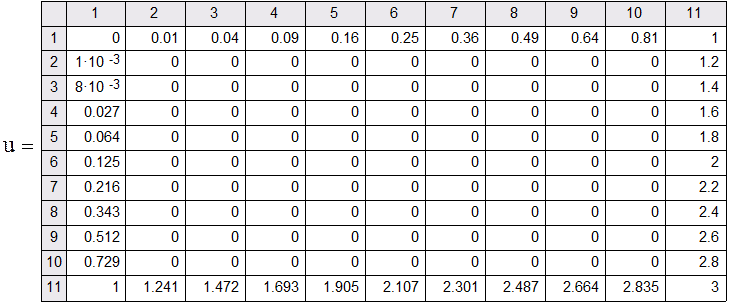
Нумерация элементов матриц начнется с 1
Краевые элементы матрицы искомой поверхности
Для начала расчета зададим начальное приближение , то есть вектор 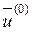
Первоначально считаем, что изменение функции происходит равномерно , т.е. с некоторым постоянным шагом :
отрезок разбит на 10 частей , следовательно изменения значения функции происходит на каждом шаге на величину
Тогда получаем, что
Только внутренние элементы матрицы
Сделав такое предположение, мы получаем полностью заполненную матрицу u , при этом надо помнить , что это только начальные (стартовые
📹 Видео
Уравнения математической физики 15+16 Задача Дирихле для уравнения Лапласа - Пуассона в кругеСкачать

6-2. Метод сетокСкачать

Методы математической физики. Задача Дирихле для уравнения Лапласа в круге. 19.05.21 Фролова Е.В.Скачать

Решение уравнения Лапласа в шареСкачать

Радкевич Е.В. - Уравнения математической физики - 6.Задача Неймана для уравнения ЛапласаСкачать

6.2 Решение задач для уравнения Лапласа в круге, вне круга и в кольцеСкачать
13.2 Разложение функции в ряд Фурье. Пример 1.Скачать

Задача Неймана для уравнения Лапласа. Третья краевая задача для уравнения ЛапласаСкачать

OTAROVA JAMILA МЕТОД ФУРЬЕ РЕШЕНИЯ КРАЕВОЙ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ЛАПЛАСА В ПРЯМОУГОЛЬНОЙСкачать

Самая простая нерешённая задача — гипотеза Коллатца [Veritasium]Скачать
![Самая простая нерешённая задача — гипотеза Коллатца [Veritasium]](https://i.ytimg.com/vi/QgzBDZwanWA/0.jpg)
Задача Дирихле для шараСкачать

Колыбасова В.В. - Методы математической физики. Семинары - 7.Внешняя краевая задача для ур.Лапласа 2Скачать
ФОРМУЛА КАРДАНО-ТАРТАЛЬЯ + РЕКЛАМА МФТИ!!!Скачать

Метод Лапласа решения ДУСкачать

Задача Дирихле для уравнения Лапласа в кольце и сектореСкачать
Уравнение Лапласа. Задача Дирихле для уравнения Лапласа внутри и вне кругаСкачать

Задача Дирихле и НейманаСкачать

Колыбасова В.В. - Методы математической физики. Семинары - 6.Внешняя краевая задача для ур.Лапласа 1Скачать