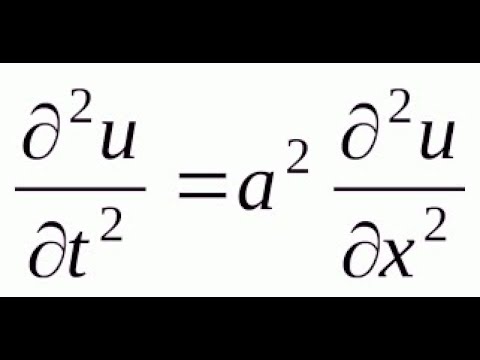Видео:6.2 Решение задач для уравнения Лапласа в круге, вне круга и в кольцеСкачать
Решение задачи Дирихле для уравнения Лапласа
Еще один наглядный пример применения метода статистических испытаний — решение задачи Дирихле для уравнения Лапласа с использованием алгоритма «блужданий но сетке». Строгое обоснование этих алгоритмов можно найти в классических работах по методу Монте-Карло.
Напомним, что уравнением Лапласа называется уравнение в частных производных
задачей Дирихле для уравнения Лапласа — задача нахождения функции, удовлетворяющей уравнению Лапласа в ограниченной связной области D и граничным условиям
на границе области 1(D).
Сформулируем задачу следующим образом: требуется применить статистическое моделирование для вычисления значения в точке Л(0,8; 0,6) функции U> удовлетворяющей в квадрате D = Рис. 2.23. Две траектории алгоритма «блужданий по сетке» Полученные по такому алгоритму 10 значений случайной величины ? оказались равными 0,3980, 0,0000, 6,5940, 0,7726, 0,5881, 0,3941, 0,5823, 0,0000, 0,5794, 0,9561. По формулам (2.19), (2.21), (2.22) получим При оценке погрешности решения задачи Дирихле для уравнения Лапласа с использованием статистического моделирования следует иметь в виду, что она складывается из погрешности разностного метода, определяемой шагом сетки, и статистической оценки погрешности, возникающей при реализации статистических испытаний. Видео:7.1 Решение уравнения Лапласа в прямоугольникеСкачать Решение краевых задач методом Монте-Карло рассмотрим на примере задачи Дирихле для уравнения Лапласа [29]. Пусть G — односвязная область, на границе которой 8G задана функция f = = f(Q), Q е 8G. Требуется найти такую функцию и(Р), которая внутри области G удовлетворяет уравнению Лапласа: Построим в области G квадратную сетку с шагом h. Узлы данной сетки делятся на два типа: регулярные и нерегулярные (см. лекция 9). Каждый регулярный узел имеет 4 соседних узла Pi, Р2, Рз, Р. из области G согласно шаблону, приведенному на рис. 9.7, б. Нерегулярный или граничный узел нс имеет ровно четырех соседей из области G. Составим разностную схему для уравнения Лапласа (15.29) на квадратной сетке и перепишем полученное уравнение следующим образом: Для решения конем но-разностной задачи (15.30) составим следующую тсоретико-вероятностную схему. Будем считать, что величина и <Р)пропорциональна плотности неких частиц в узле Р. Каждая частица может с вероятностью Vi за одни шаг по времени перейти в один из четырех соседних узлов: Рь Р2, Pi, Pi j. Таким образом, частицы, первоначально находящиеся в некотором узле, за 1 шаг по времени уходят из него, а другие частицы из соседних узлов могут прийти в исходный узел. Считаем, что частица, приходящая на границу области, поглощается. Вероятность u(P,Q) того, что частица, выйдя из регулярного узла Р, окончит блуждание в граничном узле Q, удовлетворяет условию (15.30), т. е. и краевому условию Если промоделировать блуждание частицы по решетке N раз, заставляя каждый раз ее выходить из точки Р и подсчитывать количество L ее приходов в точку Q, то отношение задачи (15.31) с краевыми условиями (15.32). Перейдем к решению задачи Дирихле в общем случае. Пусть, когда частица оказывается в точке Q, с нее берется штраф f(Q). Величина штрафа принимает значения f(Qi), . , f(Qs), где Qi, . Qs — совокупность всех граничных узлов. Согласно (15.31), (15.32) вероятность заплатить штраф f(Qj) равна u(P,Qj). Среднее значение штрафа vv(P), которое заплатит произвольная частица, выходящая из регулярной точки Р, определяется по формуле: Покажем, что выражение (15.33) удовлетворяет уравнению Действительно, подставим в (15.31) Qj вместо Q и умножим обе части на f(Qj), тогда после суммирования по j получим уравнение (15.33). Для граничных узлов функция w(P) удовлетворяет краевым условиям. Так, после подстановки Р = Q в (15.33) согласно (15.32) пропадут все слагаемые, кроме одного, т. е. т. е. vv(P) удовлетворяет конечно-разностному уравнению (15.30) и принимает на границе заданные значения. В качестве примера рассмотрим решение уравнения Лапласа ихх + иуу = О вида: В качестве области интегрирования выберем единичный квадрат, т. е. G(x,y) = [ОД] 2 . Учитывая (15.34), определим граничные условия для задачи Дирихле Определим квадратную сетку в единичном квадрате: Х„ = h(n -1), ут = = h(m — 1), h = 1/(N — 1), п.т = 1, . п. Регулярными и нерегулярными (граничными) будут соответственно узлы Найдем решение уравнения Лапласа (15.34) задачи Дирихле (15.35) методом Монте-Карло. Разыграем случайный процесс следующим образом. Выберем произвольный регулярный узел Р из набора (15.36). Выпустим из этого узла частицу и дождемся, когда она путем случайного блуждания, попадет в одну из граничных точек (15.36′). Повторим эту процедуру R раз, запоминая число приходов L(P,Q) частицы в граничные точки (15.36′). В итоге можно получить следующую расчетную схему: В листинге 15.12 приведен код программы решения уравнения Лапласа (15.34) для задачи Дирихле в единичном квадрате (15.35) по расчетной схеме (15.37). “/«Программа решения уравнения Лапласа, имеющего “/«аналитическое решение ( 15. 34) для задачи Дирихле %в единичном квадрате (15.35) по расчетной схеме %( 15. 37) методом Монте- Карло function ramble “/«Определяем количество N узлов в сетках по “/окоординатам X и у N=21; h =1. О/(N- 1); “/«Определяем сетки по координатам х и у х =0: h: 1; у =0: h: 1; “/оВносим краевые условия ( 15. 35) для задачи Дирихле u(n,l)=f(x(n),y(l)); u( n, N) =f(х( n), у( N)); end f or m=l: N u ( 1, m) =f (х( 1), у( т)); u( N, т) =f (х( N) , у( т) ); end %Определяем массив статистических испытаний с %разной длиной R=5 00: 5 0 0: 8 0 0 0; %Организуем цикл статистических испытаний с разной %длиной статистических испытаний for s =1:Iengt h(R) %Цикл статистических испытаний для каждой %регулярной точки разностной сетки “/«Определяем 4 массива соответственно %для четырех типов граничных точек “/«единичного квадрата: нижнее основание, “/«правая сторона, верхнее основание, % левая сторона Lxl=zeros(1, (N- 1) ); LxN=zer os ( 1, ( N- 1)); “/«Статистические испытания длиной R < S) for r =1: R( S) “/«Цикл, моделирующий случайные “/«блужданий на решетке “/«Подсчет числа приходов частицы %с координатами ( Р П , Р т) в одну из “/«граничных точек if ( Р n 1) &( Р т= = N) LхN( Pn- 1)=LxN( Pn-1)+1; end if ( Pn = = l)M Рт>1) Lу 1 ( Pm- 1) =Lyl( Pm- 1) +1; end end %Подсчет решения U ( X, у) по формуле ( 15. 37) uP=uP+LyN( ml)*f( x( N) , y( ml) ) ; end uP=uP+LxN( nl- 1)*f(x(n1),у(N)); end uP=uP+Lyl( ml — l)*f(x( 1), y( ml)); end u( n, m) = uP/ R( s) ; end end %Сравнение решения, полученного методом %Монте- Карло U ( П, т) , с точным решением %уравнения Лапласа (15. 34) for n = 1: N err( n, m) =abs( u(n, m)-(x(n)-y( m) )*. . . ( x( n) +y( m) -1)); end end er r or (s) =max( max(er r)); “/«Определяем аналитическое решение (15.34) в U а ( П, m) for n =1: N %Рисуем профиль аналитического решения (15.34) subplot) 1,2,1); surf(y,x,ua); %Определяем кривую зависимости ошибки решения %задачи Дирихле методом Монте- Карло от длины %статистической серии subpl ot( 1, 2, 2); semi I ogx( I ng, error); %Определяем краевые условия ( 15. 35) function Z =f ( X , у) z =0; if (y==0)|(y==l) z =x * ( x — 1) ; end if (x ==0)|(x ==1) z =y* ( 1- y); end На рис. 15.12 приведен итог работы кода программы листинга 15.12. Рис. 15.12. Пример решения краевой задачи (15.29) методом Монте-Карло На рис. 15.12, а приведен трехмерный профиль аналитического решения (15.34) уравнения Лапласа для задачи Дирихле (15.35). На рис. 15.12, б приведен график зависимости ошибки численного решения задачи Дирихле методом Монте-Карло в зависимости от длины серии статистических испытаний. Отчетливо видна тенденция уменьшения ошибки численного решения по мерс роста длины статистической серии. Видео:6-2. Метод сетокСкачать 1. Краткая теория уравнение функция лаплас программа В настоящей лабораторной работе методом сеток требуется решить задачу Дирихле для уравнения Лапласа. Эта задача ставится следующим образом. Найти непрерывную функцию и (х, у), удовлетворяющую внутри прямоугольной области уравнению Лапласа и принимающую на границе области заданные значения, т. е. Будем считать, что и(х, у) непрерывна на границе области , т. е. , , , . Выбрав шаги h, l по x и y соответственно, строим сетку , , , , где , . Вводя обозначения , аппроксимируем частные производные и в каждом внутреннем узле сетки центральными разностными производными второго порядка и заменим уравнение Лапласа конечно-разностным уравнением Погрешность замены дифференциального уравнения разностным составляет величину . Уравнения (1) вместе со значениями в граничных узлах образуют систему линейных алгебраических уравнений относительно приближенных значений функции и (х, у) в узлах сетки . Наиболее простой вид имеет эта система при : При получении сеточных уравнений (2) была использована схема узлов, изображенная на рис. 1. Набор узлов, используемых для аппроксимации уравнения в точке, называется шаблоном. В данной работе используется шаблон типа «крест». Численное решение задачи Дирихле для уравнения Лапласа в прямоугольнике состоит в нахождении приближенных значений искомой функции и(х, у) во внутренних узлах сетки. Для определения величин требуется решить систему линейных алгебраических уравнений (2). В данной лабораторной работе она решается методом Гаусса—Зейделя, который состоит в построении последовательности итераций вида (верхним индексом s обозначен номер итерации). При последовательность сходится к точному решению системы (2). В качестве условия окончания итерационного процесса можно принять Таким образом, погрешность приближенного решения, полученного методом сеток, складывается из двух погрешностей: погрешности аппроксимации дифференциального уравнения разностными; погрешности, возникающей в результате приближенного решения системы разностных уравнений (2). Известно, что описанная здесь разностная схема обладает свойством устойчивости и сходимости. Устойчивость схемы означает, что малые изменения в начальных данных приводят к малым изменениям решения разностной задачи. Только такие схемы имеет смысл применять в реальных вычислениях. Сходимость схемы означает, что при стремлении шага сетки к нулю () решение разностной задачи стремится в некотором смысле к решению исходной задачи. Таким образом, выбрав достаточно малый шаг h, можно как угодно точно решить исходную задачу. Уравнение Лапласа. Задача Дирихле для уравнения Лапласа внутри и вне кругаСкачать Метод Лапласа решения ДУСкачать Задача Дирихле для круга. Уравнение ЛапласаСкачать Уравнения математической физики 15+16 Задача Дирихле для уравнения Лапласа - Пуассона в кругеСкачать OTAROVA JAMILA МЕТОД ФУРЬЕ РЕШЕНИЯ КРАЕВОЙ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ЛАПЛАСА В ПРЯМОУГОЛЬНОЙСкачать Решение уравнения Лапласа в шареСкачать Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать Задача Дирихле для шараСкачать Колыбасова В.В. - Методы математической физики.Семинары - 15. Решение краевых задач. Функция ГринаСкачать Методы математической физики. Задача Дирихле для уравнения Лапласа в круге. 19.05.21 Фролова Е.В.Скачать Попов И.Ю. Функция Грина задачи Дирихле для уравнения ЛапласаСкачать Задача Дирихле для уравнения Лапласа в кольце и сектореСкачать Методы решения нелинейных краевых задач для ОДУСкачать Задача Неймана для уравнения Лапласа. Третья краевая задача для уравнения ЛапласаСкачать 7.2 Уравнение Лапласа в секторе и кольцевом сектореСкачать Колыбасова В.В. - Методы математической физики. Семинары - 7.Внешняя краевая задача для ур.Лапласа 2Скачать 6.1 Уравнение Лапласа в полярных координатах. Принцип решения и постановка задачСкачать>(5> 3) — конец первой траектории;
Решение краевых задач
является приближенным решением
Решение задачи Дирихле для уравнения Лапласа методом сеток
📽️ Видео
