Кр 6 дробные рациональные уравнения ответы

Видео:Дробно рациональные уравнения. Алгебра, 9 классСкачать

Алгебра 8 Макарычев Контрольная 6

Алгебра 8 Макарычев Контрольная 6 + Решения и Ответы на все 4 варианта. Представленные ниже контрольная работа ориентирована на учебник «Алгебра 8» авторов Ю.Н. Макарычева и др. под редакцией С.А. Теляковского. Ответы на контрольные работы адресованы родителям, которые смогут проконтролировать правильность выполнения заданий. Вопросы и ответы представлены в учебных целях, а также для ознакомления и покупки учебного пособия.

Контрольная работа № 6 (К-6)
по алгебре в 8 классе по учебнику Макарычева (образец)

ОТВЕТЫ на контрольную работу № 6

К-6. Решения и Ответы на Вариант 1.

К-6. Решения и Ответы на Вариант 2.

К-6. Решения и Ответы на Вариант 3.

К-6. Решения и Ответы на Вариант 4.

Алгебра 8 Макарычев Контрольная 6 + Решения и Ответы на все 4 варианта. Контрольная работа (цитаты) из учебного пособия: «Алгебра 8 класс. Дидактические материалы/ В.И. Жохов, Ю.Н. Макарычев, Н.Г. Миндюк — М.:Просвещение».

Добавить комментарий Отменить ответ

Этот сайт использует Akismet для борьбы со спамом. Узнайте, как обрабатываются ваши данные комментариев.

Видео:Дробно-рациональные уравнения. 8 класс.Скачать

Предметы

Видео:Как решать дробно-рациональные уравнения? | МатематикаСкачать

Новые работы

Видео:Решение дробных рациональных уравнений. Алгебра, 8 классСкачать

Найти контрольную:

Видео:Алгебра 8. Урок 11 - Дробно-рациональные уравненияСкачать

Авторы работ и УМК

Видео:Дробно-рациональные уравнения. Подготовка к экзаменам. 64 часть. 9 класс.Скачать

Предметы

Видео:Дробно-рациональные уравнения. Подготовка к экзаменам. 60 часть. 9 класс.Скачать

Важные страницы

Соглашение о конфиденциальности

(с) 2020-2022. Дистанционный информационный Центр НПИ (г.Москва). Бесплатная помощь школьникам, находящимся на домашнем или семейном обучении. Цитаты из учебных пособий размещены в учебных целях. Контакты: kip1979@mail.ru

Видео:ЭТО НУЖНО ЗНАТЬ — Как решать Дробно Рациональные уравнения?Скачать

Популярное

Видео:Алгебра 9 класс (Урок№17 - Дробные рациональные уравнения.)Скачать

Предупреждение

Продолжая использовать наш сайт, вы даете согласие на обработку файлов cookie, пользовательских данных (сведения о местоположении; тип и версия ОС; тип и версия Браузера; тип устройства и разрешение его экрана; источник откуда пришел на сайт пользователь; с какого сайта или по какой рекламе; язык ОС и Браузера; какие страницы открывает и на какие кнопки нажимает пользователь; ip-адрес) в целях функционирования сайта, проведения ретаргетинга и проведения статистических исследований и обзоров. Если вы не хотите, чтобы ваши данные обрабатывались, покиньте сайт.

Видео:ДРОБНО-РАЦИОНАЛЬНЫЕ УРАВНЕНИЯ ЧАСТЬ I #shorts #егэ #огэ #математика #профильныйегэСкачать

Кр 6 дробные рациональные уравнения ответы

Цель: проверить знания, умения и навыки учащихся по теме.
Тип урока: урок контроля, оценки и коррекции знаний.

ХОД УРОКА

I. Сообщение темы и цели урока

II. Общая характеристика контрольной работы

Контрольная работа составлена в 6 вариантах различной сложности (варианты 1, 2 самые простые, варианты 3, 4 сложнее и варианты 5, 6 самые сложные). При этом сложность вариантов нарастает не очень резко. Каждый вариант содержит 6 задач примерно одинаковой сложности (может быть, несколько сложнее две последние задачи).

При проверке вариантов 1, 2 оценка «5» ставится за правильное решение пяти задач, оценка «4» — четырех задач и оценка «3» — трех задач. Одна задача является резервной (или запасной) и дает некоторую свободу выбора учащимся. При таких же критериях оценки за решение задач вариантов 3, 4 дается дополнительно 0,5 балла, вариантов 5, 6 — 1 балл (т. е. оценку «5» можно получить за правильное решение четырех задач).

III. Контрольная работа в 6 вариантах

IV. Подведение итогов контрольной работы

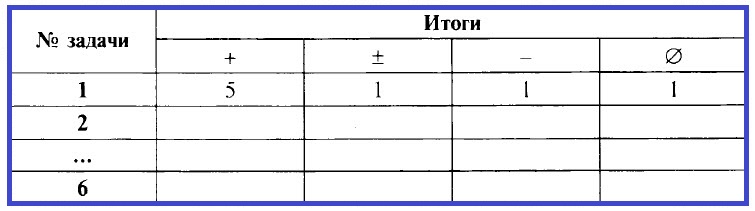
1. Распределение работ по вариантам и результаты решения. Данные о результатах работы удобно заносить в таблицу (для каждой пары вариантов).

Обозначения:
+ (число решивших задачу правильно или почти правильно);
± (число решивших задачу со значительными погрешностями);
– (число не решивших задачу);
∅ (число не решавших задачу).

1. Типичные ошибки, возникшие при решении задач.
2. Наиболее трудные задачи и их разбор (учителем или школьниками, решившими их).
3. Разбор всей контрольной работы (вывесить на стенде ответы к заданиям и разобрать наиболее трудные варианты).

V. Разбор задач ( ответы и решения )

VI. Подведение итогов урока

Вы смотрели: Поурочное планирование по алгебре для 8 класса. УМК Макарычев (Просвещение). ГЛАВА III. КВАДРАТНЫЕ УРАВНЕНИЯ. § 9. Дробные рациональные уравнения (11 ч). Урок 63. Контрольная работа № 6 «Дробные рациональные уравнения» + ОТВЕТЫ и РЕШЕНИЯ.

Видео:Дробно-рациональные уравнения + Бонус: треугольник Паскаля | МатематикаСкачать

Контрольная работа по алгебре в 8 классе на тему «Дробно — рациональные уравнения»

Контрольная работа содержит 4 варианта с подробным решением.

Просмотр содержимого документа
«Контрольная работа по алгебре в 8 классе на тему «Дробно — рациональные уравнения»»

В а р и а н т 1

1. Решите уравнение:

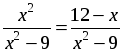
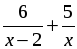
а) ; б) = 3.

2. Из пункта А в пункт В велосипедист проехал по одной дороге длиной 27 км, а обратно возвращался по другой дороге, которая была короче первой на 7 км. Хотя на обратном пути велосипедист уменьшил скорость на 3 км/ч, он все же на обратный путь затратил времени на 10 минут меньше, чем на путь из А в В. С какой скоростью ехал велосипедист из А в В?

В а р и а н т 2

1. Решите уравнение:

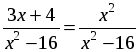
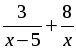
а) ; б) = 2.

2. Катер прошёл 12 км против течения реки и 5 км по течению. При этом он затратил столько времени, сколько ему потребовалось бы, если бы он шёл 18 км по озеру. Какова собственная скорость катера, если известно, что скорость течения реки равна 3 км/ч.

В а р и а н т 3

1. Решите уравнение:

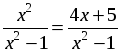
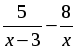
а) ; б) = 3.

2. Из пункта А в пункт В велосипедист проехал по дороге длиной 48 км, обратно он возвращался по другой дороге, которая короче первой на 8 км. Увеличив на обратном пути скорость на 4 км/ч, велосипедист затратил на 1 час меньше, чем на путь из А в В. С какой скоростью ехал велосипедист из пункта А в пункт В?

В а р и а н т 4

1. Решите уравнение:

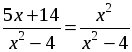
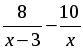
а) ; б) = 2.

2. Катер прошёл 15 км против течения и 6 км по течению, затратив на весь путь столько же времени, сколько ему потребовалось бы, если бы он шёл 22 км по озеру. Какова собственная скорость катера, если известно, что скорость течения реки равна 2 км/ч?

Решение вариантов контрольной работы

В а р и а н т 1

1. а) 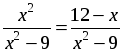. Общий знаменатель х 2 – 9.

По теореме, обратной теореме Виета, х₁ = 3; х₂ = –4.

Если х = 3, то х 2 – 9 = 0.

Если х = –4, то х 2 – 9 ≠ 0.

б) 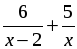= 3. Общий знаменатель х (х – 2).

D = (–17) 2 – 4 · 3 · 10 = 289 – 120 = 169, D 0, 2 корня.

x₁ = 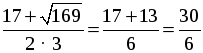= 5;

x₂ = .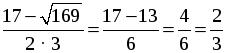

Если х = 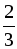, то х (х – 2) ≠ 0.

О т в е т: а) –4; б) 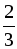; 5.

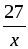
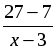
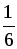
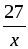
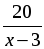
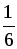
2. Пусть х км/ч – скорость велосипедиста, с которой он ехал из А в В, тогда (х – 3) км/ч – скорость, с которой он ехал обратно. На путь из А в В он затратил ч, а обратно ч. Зная, что на обратный путь он затратил на 10 мин ( часа) меньше, составим уравнение:

– = . Общий знаменатель 6х (х – 3).

D = (–45) 2 – 4 · 486 = 81, D 0, 2 корня.

x₁ = 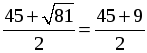= 27;

x₂ = 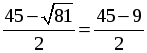= 18.

Ни один из корней не обращает знаменатель в нуль, но корень х = 27 не удовлетворяет условию задачи (слишком большая скорость для велосипедиста).

О т в е т: 18 км/ч.

В а р и а н т 2

1. а) 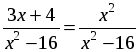. Общий знаменатель х 2 – 16.

По теореме, обратной теореме Виета х₁ = 4; х₂ = –1.

Если х = 4, то х 2 – 16 = 0.

Если х = – 1, то х 2 – 16 ≠ 0.

б) 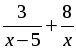= 2. Общий знаменатель х (х – 5).

D = (–21) 2 – 4 · 2 · 40 = 441 – 320 = 121, D 0, 2 корня.

x₁ = 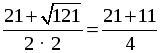= 8;

О т в е т: а) –1; б) 2,5; 8.

2. Пусть х км/ч – собственная скорость катера, тогда против течения он шёл со скоростью (х – 3) км/ч, по течению – (х + 3) км/ч и по озеру – х км/ч. Против течения он шёл ч, по течению ч, а по озеру он шёл бы ч. Зная, что на все плавание по реке он затратил бы столько же времени, сколько на плавание по озеру, составим уравнение:

12х 2 + 36х + 5х 2 – 15х – 18х 2 + 162 = 0;

D = (–21) 2 – 4 · 162 = 441 + 648 = 1089, D 0, 2 корня.

Ни один из корней не обращает знаменатель в нуль, но х = –6 не удовлетворяет условию задачи.

О т в е т: 27 км/ч.

В а р и а н т 3

1. а) 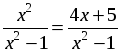. Общий знаменатель х 2 – 1.

По теореме, обратной теореме Виета, х₁ = 5; х₂ = –1.

Если х = 5, то х 2 – 1 ≠ 0.

Если х = –1, то х 2 – 1 = 0.

б) 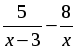= 3. Общий знаменатель х (х – 3).

По теореме, обратной теореме Виета, х₁ = 4; х₂ = –2.

О т в е т: а) 5; б) –2; 4.

2. Пусть х км/ч – скорость, с которой велосипедист ехал из А в В, тогда (х + 4) км/ч – скорость, с которой он ехал обратно. На путь из А в В он затратил ч, а обратно ч. Зная, что на обратный путь он затратил на 1 ч меньше, составим уравнение:

– = 1. Общий знаменатель х (х + 4).

Ни один из корней не обращает знаменатель в нуль, но корень х = –12 не удовлетворяет условию задачи.

О т в е т: 16 км/ч.

В а р и а н т 4

1. а) 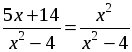. Общий знаменатель х 2 – 4.

По теореме, обратной теореме Виета, х₁ = 7; х₂ = –2.

Если х = 7, то х 2 – 4 ≠ 0.

Если х = –2, то х 2 – 4 = 0.

б) 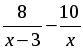= 2. Общий знаменатель х (х – 3).

По теореме, обратной теореме Виета, х₁ = 5; х₂ = –3.

О т в е т: а) 7; б) –3; 5.

2. Пусть х км/ч – собственная скорость катера, тогда против течения он шёл со скоростью (х – 2) км/ч, по течению – (х + 2) км/ч и по озеру – х км/ч. Против течения он шёл ч, по течению ч, а по озеру он шёл бы ч. Зная, что на все плавание по реке он затратил бы столько же времени, сколько на плавание по озеру, составим уравнение:

15х 2 + 30х + 6х 2 – 12х – 22х 2 + 88 = 0;

Ни один из корней не обращает знаменатель в нуль, но корень х = –4 не удовлетворяет условию задачи.

📽️ Видео

Дробно-рациональные уравнения. Подготовка к экзаменам. 61 часть. 9 класс.Скачать

Дробно рациональное уравнение. ОГЭ математика задача 4 (тип 4) 🔴Скачать

8 класс. Контрольная №6 (из 10). Тема: Квадратные уравнения Дробные рациональные уравнения. :)Скачать

#136 Урок 61. Дробно-рациональные уравнения. Рациональные уравнения, приводящиеся к квадратным.Скачать

Дробно-рациональные уравнения. Подготовка к экзаменам. 57 часть. 9 класс.Скачать

Дробные рациональные уравнения | 9 класс МакарычевСкачать

Дробные рациональные уравнения | Алгебра 9 класс #13 | ИнфоурокСкачать

Как решать уравнения с дробью? #shortsСкачать

Алгебра 8 класс (Урок№31 - Решение дробных рациональных уравнений.)Скачать