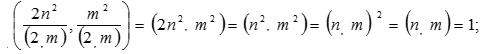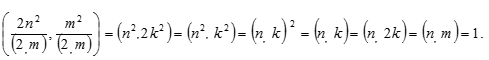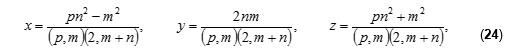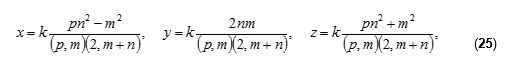Аннотация: В работе предпринята попытка найти общие полные решения некоторых диофантовых уравнений второй степени с тремя переменными, проследить некоторые закономерности, предложить общие подходы, которые будучи элементарными, тем не менее, приводят к решению подобных уравнений. Использование арифметических функций позволило записать найденные решения в виде единой формулы без ограничений на используемые параметры.
Ключевые слова: диофантово уравнение, уравнения второй степени от трёх переменных.
Работа посвящена одному из центральных разделов теории чисел – теории диофантовых уравнений.
В прошлом году мы работали с уравнением Пифагора: а² + b² = с², где а, b, с – натуральные числа, имеющее бесконечное множество решений. Работа была построена на отыскании общей формулы для задания всех решений уравнения Пифагора. Дело в том, что в источниках, изученных нами, нет единой формулы для задания всех решений. Известные решения состояли из объединения двух формул. Исключением оказалась аннотация работы казахстанского учёного Кожегельдинова С. Ш. [1], который предложил одну общую формулу, задающую все решения уравнения Пифагора на основе использования арифметических функций. В своей работе мы самостоятельно нашли способы вывода такой формулы, показали при каких параметрах из выведенной нами формулы можно получить решения, предлагавшиеся другими авторами [2] – [4], применили полученные знания к решению уравнения Пифагора в числах, обратных натуральным, рассмотрели перспективы дальнейшей работы над отысканием решений диофантовых уравнений.
В рамках рассмотренных перспектив и была построена наша нынешняя работа.
Новизна данной работы состоит в применении арифметических функций при решении рассматриваемых задач, что позволяет записать одну общую формулу решений, вместо объединения нескольких формул, предлагаемых в известной литературе, при этом, выбранные параметры не имеют ограничений (например, по чётности).
Решение неопределённых уравнений имеет не только теоретический интерес. К диофантовым уравнениям приводят задачи, по смыслу которых неизвестные значения величины могут быть только целыми числами. Например, космические, астрономические задачи, задачи арифметической геометрии. Связь между данным вопросом теории чисел и свойствами правильных точечных решёток позволила развить и методы изучения последних, сыгравших чрезвычайно важную роль в решении ряда основных задач кристаллографии. Непосредственно задачи кристаллографии, а именно описание кристаллических решёток с помощью целочисленных уравнений, которые задают положение атомов в структуре кристаллической решетки, и послужило отправным пунктом для написания этой работы.
Имеется практическая необходимость выработать стандартный способ нахождения всех решений диофантовых уравнений второй степени и выше с двумя и более переменными, но на сегодняшний день, не существует единого способа или приёма, позволяющего решить любое диофантово уравнение, если его степень выше первой.
Указанное противоречие позволило сформулировать цель и задачи нашей работы, исходя из уровня личных знаний.
Нахождение способа задания общей формулы всех решений некоторых диофантовых уравнений второй степени с тремя неизвестными на множестве натуральных чисел.
Если удастся найти способ задания общей формулы для нахождения всех решений некоторых диофантовых уравнений второй степени с тремя неизвестными, то возможно удастся применить полученные результаты и для решения других задач данного раздела математики, а может быть и для диофантовых уравнений определённых видов второй и выше степени с двумя и более переменными, так как многие проблемы математики решались для частных случаев, а после обобщались.
Объект исследования: некоторые диофантовы уравнения второй степени с тремя переменными.
Предмет исследования: процесс нахождения общего решения некоторых неопределённых уравнений второй степени с тремя переменными на множестве натуральных чисел.
Задачи:
1. Познакомиться с методами и приёмами, использовавшимися для решения уравнения Пифагора и задач, связанных с ним.
2. Рассмотреть возможность использования арифметических функций к решению близких диофантовых уравнений.
3. Самостоятельно вывести общую формулу некоторых диофантовых уравнений второй степени с тремя переменными.
4. В случае удачи, рассмотреть возможность применения полученных результатов к решению более общих задач неопределённого анализа.
Планирование ожидаемых результатов:
Работа над проектом поможет найти общую формулу решений некоторых диофантовых уравнений второй степени с тремя переменными и оценить перспективы применения полученных результатов для решения других неопределённых уравнений второй степени.
Полученные результаты могут быть использованы в кристаллографии. Например, при изучении пространственной изомерии, структур решёток веществ, имеющих плоское или плоско-сетчатое строение, как, например, графит.
Критерии оценки ожидаемых результатов:
— выявление возможности использования арифметических функций к решению некоторых диофантовых уравнений второй степени с тремя неизвестными на множестве натуральных чисел;
— нахождение единой формулы всех решений некоторых диофантовых уравнений второй степени с тремя переменными;
— рассмотрение возможности использования полученных результатов для решения близких задач.
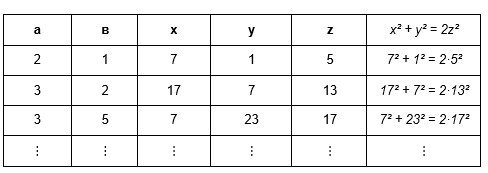
При k = 1 из формулы (8) получается формула (7). Положив в формуле (8) а и в конкретными числами найдём частные решения уравнения (1). Например, при k = 1
является квадратом некоторого числа, другое – удвоенным квадратом того же или другого числа. Иначе говоря, если первое число является квадратом некоторого числа, то второе – удвоенным квадратом того же или другого числа и наоборот, если второе число является квадратом некоторого числа, то первое – удвоенным квадратом того же или другого числа. При этом нетрудно доказать, что если числа m и n взаимно простые, то и числа (*) будут взаимно простыми. § 2.2 Решить уравнение х² + 2у² = z² (9) где x, y, zϵ N.
Прежде чем переходить к решению уравнения (9) заметим, что для любых чисел m, n ϵ N одно из двух чисел
В самом деле, пусть (m, n) = 1. Тогда, если:
1) m – нечётно, то при любой чётности n число (2, m) = 1 и, следовательно,
2) m – чётно (следовательно, n – нечётно), то при (2, m) = 2. Пусть m = 2k, где k ϵ N. Поэтому будем иметь, что
Таким образом, в обоих случаях получаем, что числа (*) взаимно простые, если (m, n) = 1.
Очевидно, что если ‹a, b, c› – решение (26), то и любая тройка ‹ka, kb, kc›, где k ϵ N, также является решением (26). Поэтому достаточно найти общую формулу всех основных троек, то есть таких, для которых (х, у, z) = 1. Для отыскания такой формулы будем рассматривать не уравнение (26), а равносильное ему уравнение
где x, y, zϵ N, z– x ˃ 0. Так как левая часть уравнения (10) делится на 2, то и правая часть должна быть чётной. Если
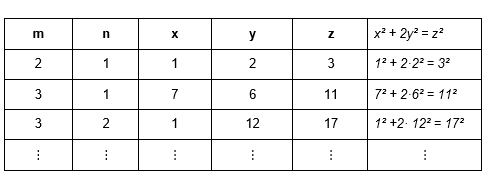
Положив в формуле (14) k= 1 получим формулу (13), которая является общей формулой всех основных троек. Подставив в формулу (14) конкретные числаmи nмы получим частные решения уравнения (9). Например, при k= 1 имеем
Легко показать, что если в уравнении (12) положить
§ 2.3 Рассмотрим более сложное уравнение
х² + ру² = z² (16)
При решении этого равнения будем пользоваться обозначениями и результатами, полученными в предыдущих пунктах.
Если р|х, то обозначив х = рх1, можно переписать уравнение (16) как р² х1² + ру² = z². Откуда следует, что р|z; положив z = рz1 имеем рх1² + у² = рz1². Следовательно, р|у, но тогда (х, у, z) = р≠1 в общем случае. Однако, очевидно, что если ‹х, у, z› – решение уравнения (16), то и ‹kх, kу, kz›, где k ϵ N, также является решением уравнения (16), а, значит, для решения данного уравнения нам достаточно найти основные тройки, то есть такие, для которых (х, у, z) = 1. Следовательно предположение о том, что р|х неприемлемо. Таким образом, потребуем, чтобы выполнялось условие (х, ру) = 1. Аналогично, (х, рz) = 1.
Перепишем уравнение (16) следующим образом
Если z и х – разной чётности, то либо
a) z + х = рu, z – х = v,
b) z + х = u, z – х = рv,
Рассмотрим случай а). В этом случае положим
Формула (23) обращается в формулу (21), если (р, m) = 1 и в формулу (22), если (р, m) = р. Других вариантов быть не может, так как р – простое число.
Формулы (20) и (23), в свою очередь, так же можно объединить в единую формулу,
где р, m, nϵ N, (m, n) = 1, рn² > m², которая является общей формулой всех основных троек и не содержит более ограничений чётности на числа mи n. Очевидно, что если mи n – нечётны, то (2, m+n) = 2 и из формулы (24) получается формула (20), если же mи n – разной чётности, то (2, m+n) = 1 и формула (24) обращается в формулу (23). Других вариантов нет, поскольку (m, n) = 1.
Теперь несложно написать и общую формулу всех троек
Легко показать, что при р = 2 из формул (25) получаются формулы (14), являющиеся решениями уравнения (9), которое, в свою очередь, получается из уравнения (16) при р = 2.
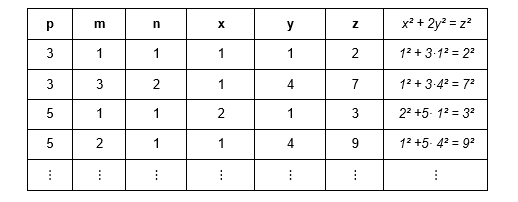
Полагая в уравнении (16) р конкретным натуральным числом, получим частные уравнения, для которых при фиксированных натуральных чисел m и nможно найти частные решения. Например, положив р = 3 уравнение (16) примет вид: х² + 3у² = z²
где р, x, y, zϵ N. Варьируя параметры в формуле (25) получим частные решения уравнения (16). Несколько примеров при к = 1 содержит следующая таблица:
Исследуемое в работе противоречие не было устранено, однако мы смогли применить рассмотренные в предыдущей работе приёмы для нахождения стандартных способов отыскания всех решений некоторых диофантовых уравнений второй степени с тремя неизвестными.
Выводы
Итак, в результате проведённого исследования были найдены общие формулы решения некоторых диофантовых уравнений второй степени от трёх переменных. На основе полученных решений, можно сделать вывод, что найденные подходы могут быть использованы к нахождению общих решений близких диофантовых уравнений.
То есть, нашла подтверждение гипотеза о том, что если найти способ задания общей формулы для нахождения всех решений некоторых диофантовых уравнений второй степени с тремя неизвестными, то возможно удастся применить полученные результаты и для решения других задач данного раздела математики.
Рассмотренные объект и предмет исследования позволили достигнуть поставленной цели: на основе ранее полученных результатов были найдены способы задания общей формулы всех решений некоторых диофантовых уравнений второй степени с тремя неизвестными на множестве натуральных чисел.
Литература, в которой освещается проблема диофантовых уравнений, в том числе уравнение Пифагора, не многочисленна. В изученной нами литературе рассмотрены некоторые способы нахождения решений уравнения Пифагора и уравнения х² + 2у² = z² [2, 3, 4]. Приводятся общие формулы решения для указанных уравнений [1, 3]. Но в тех источниках, которыми мы располагаем, не приводятся расчёты подобные сделанным в данной работе. Так же нами показано как можно получить все классические формулы, из найденных нами формул, варьируя параметры. Мы не располагаем данными об освещении решений уравнений х² + у² = 2z² и х² + ру² = z² , где р – простое число, а так же о том рассматривались ли они в каких-либо источниках.
Ссылки на источники:
- Кожегельдинов С. Ш. О задачах, связанных с пифагоровыми тройками // Межвузовская конференция, посвящённая 150–летию со дня рождения Абая. СГУ имени Шакарима,1991 г., стр. 132 – 133
- Башмакова И. Г. Теория чисел. М.: Наука, 1992 г.
- Гельфонд А. О. Решение уравнений в целых числах. М.: ИТКЛ, 1987г.
- Литцман В. Теорема Пифагора и пифагоровы тройки. М.: Знание, 2008 г.
- Кожегельдинов некоторые элементы теории диофантовых уравнений
- Кожегельдинов, Сагдулла Шаяхметович — Некоторые классические диофантовы уравнения от трех и более переменных : [в 5 томах]
- Карточка
- Marc21
- Описание
- Состав
- Исследовательская работа по математике по теме: “Диофантовы уравнения, типы и способы решения»
- Основая часть.
- 1.Историческая справка.
- 3. Диофантовы уравнения в заданиях С5 ЕГЭ.
- 4.Практическое применение теории диофантовых уравнений.
- Заключение.
- 📺 Видео
Видео:Классический способ решения Диофантовых уравнений ➜ Решите уравнение в целых числах ➜ 13x-7y=6Скачать

Кожегельдинов некоторые элементы теории диофантовых уравнений
» в конце слова из фразы. Например:
Критерий близости
» в конце фразы. Например, для того, чтобы найти документы со словами исследование и разработка в пределах 2 слов, используйте следующий запрос:
Релевантность выражений
Поиск в интервале
Кожегельдинов, Сагдулла Шаяхметович — Некоторые классические диофантовы уравнения от трех и более переменных : [в 5 томах]
Карточка
Кожегельдинов, Сагдулла Шаяхметович.
Некоторые классические диофантовы уравнения от трех и более переменных : [в 5 томах] / С. Ш. Кожегельдинов. — Семей : Талант, 2008-. — 21 см.; ISBN 978-61-7037-16-1
Физико-математические науки — Математика — Теория чисел — Алгебраическая теория чисел — Диофантовы уравнения. Неопределенные уравнения
Marc21
| LDR | 00941nam#a2200193#ia4500 |
| 001 | 004113945 |
| 005 | 20081106105807.0 |
| 008 | 081031m2008####kz#||||#######0||#|#rus|d |
| 017 | ## $a И11905-08 $b РГБ |
| 020 | ## $a 978-61-7037-16-1 |
| 040 | ## $a RuMoRGB $b rus $e rcr |
| 041 | 0# $a rus |
| 044 | ## $a kz |
| 084 | ## $a В142.2,0 $2 rubbk |
| 100 | 1# $a Кожегельдинов, Сагдулла Шаяхметович |
| 245 | 00 $a Некоторые классические диофантовы уравнения от трех и более переменных : $b [в 5 томах] $c С. Ш. Кожегельдинов |
| 260 | ## $a Семей $b Талант $c 2008- |
| 300 | ## $c 21 см |
| 650 | #7 $a Физико-математические науки — Математика — Теория чисел — Алгебраическая теория чисел — Диофантовы уравнения. Неопределенные уравнения $2 rubbk |
Описание
| Автор | Кожегельдинов, Сагдулла Шаяхметович |
|---|---|
| Заглавие | Некоторые классические диофантовы уравнения от трех и более переменных : [в 5 томах] |
| Дата поступления в ЭК | 31.10.2008 |
| Каталоги | Книги (изданные с 1831 г. по настоящее время) |
| Сведения об ответственности | С. Ш. Кожегельдинов |
| Выходные данные | Семей : Талант, 2008- |
| Физическое описание | 21 см |
| ISBN | ISBN 978-61-7037-16-1 |
| Тема | Физико-математические науки — Математика — Теория чисел — Алгебраическая теория чисел — Диофантовы уравнения. Неопределенные уравнения |
| BBK-код | В142.2,0 |
| Язык | Русский |
Состав
Некоторые классические диофантовы уравнения от трех и более переменных : [в 5 томах] / С. Ш. Кожегельдинов. — Семей : Талант, 2008-. — 21 см.
Т. 4: Арифметические функции и классические диофантовы уравнения. — 2008. — 97, [1] с.; ISBN 978-601-7037-17-8 ещё
Хранение: FB 2Р 20/183;
Кожегельдинов, Сагдулла Шаяхметович.
Некоторые классические диофантовы уравнения от трех и более переменных : [в 5 томах] / С. Ш. Кожегельдинов. — Семей : Талант, 2008-. — 21 см.
Т. 5: Арифметические функции и классические системы диофантовых уравнений. — 2008. — 97, [1] с.; ISBN 978-601-7037-18-5 ещё
Хранение: FB 2Р 20/183;
Видео:ПЕРЕЧНЕВЫЕ ОЛИМПИАДЫ. Диофантовы уравненияСкачать

Исследовательская работа по математике по теме: “Диофантовы уравнения, типы и способы решения»
Международная научно-практическая конференция
«Первые шаги в науку»
Исследовательская работа по математике по теме:
“Диофантовы уравнения, типы и способы решения»
Предметная область: математика
Работу выполнила:Хомякова Ольга, ученица 10 класса
Учитель:, учитель математики
МБОУ средняя школа №4 с углубленным изучением отдельных предметов
2.Виды диофантовых уравнений и их классификация
3. Диофантовые уравнения в части С ЕГЭ-13
4. Практическое применение теории диофантовых ур-ний -16
В школьном курсе математики диофантовы уравнения практически не изучаются, но, например, в заданиях группы С6 в ЕГЭ встречаются уравнения 2-ой степени. Также с этими заданиями я сталкивалась в математических олимпиадах. Я заинтересовалась этой темой для того, чтобы успешно сдать Единый Государственный Экзамен и принимать участие в олимпиадах и конкурсах. Помимо этого, меня заинтересовала практическая направленность области этой темы.
Предметная областью моего исследования является математика.
Объект работы — диофантовы уравнения, типы и способы их решения.
1. Повысить уровень математической культуры ;
2. Развить в себе навыки исследовательской деятельности в области математики;
3. Научиться самой и научить других решать диофантовы уравнения эффективными методами;
4. Применять эти методы решения к задачам из повседневной жизни человека, а также к задачам, предлагаемым на вступительных экзаменах в ВУЗы и в олимпиадных заданиях;
5. Классифицировать методы решений дифференциальных уравнений;
6. Составить сборник задач с решениями в помощь ученикам нашей школы.
1. изучить исторические корни ;
2. научиться пользоваться научной литературой, строить графики в современных компьютерных программах, быстро и грамотно находить информацию в интернете;
3. исследовать методы решения задач, приводимых к уравнениям первой степени с двумя переменными, выбрав самые удобные и простые;
4. научиться решать задачи из повседневной жизни, вступительных экзаменов в ВУЗы экономического направления и олимпиадных заданий, применив изученные ранее методы;
5. разработать методическое пособие для всех интересующихся (подобрать или самим составить задачи с экономическим содержанием, приводящие к решению уравнений с двумя переменными).
Методы исследования : анализ, синтез, сравнение, противопоставление, ранжирование, прогнозирование, наблюдение.
Гипотеза: изучив типы, классифицировав диофантовы уравнения по способам решения можно успешно справиться с решением текстовых задач, задач с практическим содержанием и с частью заданий С6 ЕГЭ.
1. Изучение истории появления диофантовых уравнений, основной литературы по этой теме;
2. Изучение способов и методов решения диофантовых уравнений;
3. Попытка их классификации ;
4. Поиск практической значимости данной темы.
Видео:Как решать Диофантовы уравнения ★ 9x+13y=-1 ★ Решите уравнение в целых числахСкачать

Основая часть.
Видео:Теория чисел. 6. Методы решения сравнений 1 й степениСкачать

1.Историческая справка.
Диофант( вероятно 3 в. н. э. – древнегреческий математик из Александрии)
Диофантовы уравнения – алгебраические уравнения или системы алгебраических уравнений с целыми коэффициентами, у которых отыскиваются целые или рациональные решения.
Эти уравнения названы по имени Диофанта ( вероятно 3 в. н. э. – древнегреческий математик из Александрии), изучавшего такие уравнения.
Диофант представляет одну из наиболее трудных загадок в истории науки. Нам неизвестно ни время, когда он жил, ни предшественники, которые работали бы в той же области. Достаточно решить уравнение первой степени с одним неизвестным – и мы узнаем, что Диофант прожил 84 года.
Наиболее загадочным представляется творчество Диофанта. До нас дошло шесть из тринадцати книг, которые были объединены в “Арифметику”, стиль и содержание этих книг резко отличается от классических античных сочинений по теории чисел и алгебры, образцы которых мы знаем по “Началам” Евклида, его “Данным”, леммам из сочинений Архимеда и Аполлония. “Арифметика”, несомненно, явилась результатом многочисленных исследований, которые остались совершенно неизвестными. Число неизвестных диофантовых уравнениях превосходит число уравнений, и поэтому иногда их называют неопределенными.
Диофантовы уравнения впервые обстоятельно исследовались в книге Диофанта “Арифметика”. Такие уравнения имеют некоторые особенности:
1. Они сводятся к уравнениям или системам уравнений с целочисленными коэффициентами.
2. Требуется найти только целые, часто натуральные решения.
2. Определение, виды диофантовых уравнений и способы их решений.
Итак, диофантовым уравнением для целочисленных переменных х 1 , х 2 , …, х n называется уравнение, которое может быть приведено к виду
Где Р — некоторый многочлен от указанных переменных с целыми коэффициентами.
Простейшим диофантовым уравнением является уравнение вида ax + by = c , где a и b – целые взаимно простые числа. Такое диофантово уравнение имеет бесконечное число решений: если x 0 и y 0 – одно решение, то числа x = x 0 + bn и y = y 0 — an ( где n — любое целое число ) также будут решениями, которыми исчерпывается вся совокупность решений.
Виды диофантовых уравнений:
Итак, я предлагаю рассмотреть решение следующего уравнения:
Так как 8 и 9 взаимно простые числа, т. е. наибольший общий делитель 8 и 9 равен 1 то решение существует. Одно из решений найдем подбором:
x 0 =2, y 0 =3. Остальные решения вычисляются по формулам:

Если наибольший общий делитель d коэффициентов а и b больше 1, а свободный член с не делится на d , то уравнение ах + by = c не имеет решений в целых числах.
А теперь рассмотрим линейное диофантово уравнение, которое не имеет целых решений:
Для доказательства того, что это уравнение не имеет целых решений, необходимо вынести за скобки общий множитель 5, получим 5( x +7 y )=17 . Тогда левая часть уравнения делится на 5, а правая часть на 5 не делится. Значит, уравнение не имеет решений в целых числах.
Любое уравнение ах + by = с , где НОД(а, b ) = 1, имеет хотя бы одно решение в целых числах.
К диофантовому уравнению приводит и такая задача:
На покупку нескольких открыток по 11 рублей и конвертов по 13 рублей потратили всего 61 рубль. Сколько купили открыток?
Давайте обозначим число открыток через х, а число конвертов через y , то задача сводится к уравнению 11 x +13 y =61 . Очевидно, что по условию задачи здесь пригодны лишь целые положительные числа. Методом подбора найдем такие числа. Данное уравнение имеет только одно такое решение: x =2, y =3 .
Еще в Древнем Вавилоне родилась задача о построении прямоугольного треугольника с попарно соизмеримыми сторонами. Соизмеримость сторон означает, что найдется такой масштаб, в котором катеты и гипотенуза будут выражаться натуральными числами x и y , но тогда:
Таким образом, вавилонская задача сводится к задаче построения всех троек натуральных чисел x , y , z удовлетворяющих предыдущему уравнению. Пифагорейцы нашли способ построения всех его решений. Но, возможно, этот способ был найден еще раньше в Вавилоне и Индии. Так или иначе, решения ( x , y , z ) уравнения x ^2+ y ^2= z ^2 принято называть пифагоровыми тройками: x =2 n +1; y =2 n ( n +1) ; z =2 n ^2+2 n +1 , n принадлежит Z . Примеры пифагорейских троек: 3, 4, 5; 6, 8, 10; 5, 12, 13.
Однако эти формулы не дают возможности найти все пифагорейские тройки чисел, имеющие выбранное исходное число. Формулы Пифагора и Платона и их различные модификации дают только частные решения. Приведем еще примеры пифагорейских троек чисел, которые нельзя получить по указанным формулам: 72, 65, 97; 72, 320, 328.
Эти и другие пифагорейские тройки чисел дает вавилонская клинописная табличка, относимая к эпохе гг. до н. э. Метод вавилонян дает возможность найти все пифагорейские тройки, содержащие выбранные исходные числа.
Известный в теории диофантовых уравнений является проблема Ферма ( Пьер Ферма ( ) – французский математик). Эта проблема носит название великой теоремы Ферма.
Она была сформулирована Ферма примерно в 1630 году на полях книги Диофанта “Арифметика”. Общее доказательство получил английский математик Уайлс в 1995 году.
2уравнения второй степени:
Я предлагаю вам решить 4 уравнения:
Итак, попробуем найти решение для первого уравнения:
Так как число 11 имеет делители только 1 и 11, то возможны следующие сочетания сомножителей:
1. 



Тогда x= -11, y= 10
Ответ запишем в следующем виде: (1;10), (11;-10), (-1;-10), (-11;10).
Задачу №2 я предлагаю решить аналогичным способом, при помощи 4 систем.

Тогда х=2, у=1/3 (т. е. система не имеет решения в целых числах).



Тогда х=-2, у=-1/3 (т. е. система не имеет решения в целых числах).
Из этих пар чисел видно, что уравнение не имеет решений в целых числах.
Задачу № 3 тоже можно решить при помощи 4 систем. Решив системы, получим следующие пары чисел: ( 0;-1), (0;1), ( y =4/5), ( y = -4/5)
Последние две системы не имеют целых решений, следовательно, ответ: (0;-1),(0;1).
Последнее уравнение не похоже на 3 предыдущих.
Преобразуем заданное уравнение (вынесем за скобки y и вычтем и прибавим число 3):
В результате преобразований получаем уравнение:
Так как число 2 может быть представлено 4 способами в виде произведения целых чисел 2= (-2) * (-1); 2=( -1) * ( -2); 2=1 * 2; 2= 2*1, то возможны четыре системы. Из них получаем четыре пары чисел (1; -2), (2; -3), ( 4;1), (5;0). Ответом этого уравнения будут являться все 4 пары.
Запишем данное уравнение в виде (3 x – y ) * (3 x + y )=14 . Так как число 14 с учетом порядка следования множителей может быть представлено в виде произведения целых чисел следующим образом: 14=( -2) * (-7); 14=( -7) *(-2); 14=( -1) * ; 14= (-14) * (-1); 14= 2 * 7; 14= 7 * 2; 14= 1* 14; 14= 14* 1, то будет 8 случаев.
Решив все 8 систем, мы получаем дробные значения, а значит, что это уравнение не имеет решений в целых числах.
Разложим левую часть заданного уравнения на линейные множители: Уравнение примет вид: (3 x + 2 y )( x + y )=7
Так как 7 число простое, то оно равно произведению двух целых чисел в четырех случаях. Решив все 4 системы, получим пары чисел (-5;4), (5; -4), ( -13;20), ( 13;-20). Эти числа и будут ответом.
x^2 + y^2 – 2x + 4y=-5
В левой части уравнения выделим полный квадрат:
x^2 – 2x + 1 + y^2 + 4y + 4=0
Сумма квадратов равна 0 лишь в одном случае

Решив систему, получим, что x = 1, y = -2
x^2 – 6x + y^2 + 6y + 18=0
Докажем, что это уравнение имеет единственное целочисленное решение.
В левой части уравнения выделим полные квадраты :
( x – 3 )^2 + ( y + 3 )^2=0
Данное уравнение имеет решение, когда

Теперь я предлагаю рассмотреть графический метод решения диофантовых уравнений.
Алгоритм построения графика уравнения ах + by + с = 0:
1. Придать переменной х конкретное значение х= х1; найти из уравнения ах1 + by + c = 0 соответствующее значение y = y 1.
2. Придать переменной х другое значение х=х2; найти из уравнения ах2 + by + c = 0 соответствующее значение y = y 2.
3. Построить на координатной плоскости х Oy две точки (х1;у1) и (х2;у2).
4. Провести через эти две точки прямую – она и будет графиком уравнения ах + by + с = 0.
Так, например, уравнение 5 x + 7 y =17 можно решить графическим методом, изобразив прямую 5 x + 7 y = 17, и определив на этой прямой точки, обе координаты которых будут в данном случае натуральными числами.
Целые решения: (2 ;1),( 9;-4), ( 16;-9),(-5;6),(-12;11)
Видео:Математика. Линейные диофантовы уравнения с двумя неизвестными. Центр онлайн-обучения «Фоксфорд»Скачать

3. Диофантовы уравнения в заданиях С5 ЕГЭ.
Необходимо найти все пары (х, у) целых чисел, удовлетворяющих системе неравенств:

Рассмотрим на координатной плоскости области, которые описываются заданными неравенствами. А затем выберем в них лишь точки с целочисленными координатам х, у.
Получаем два случая:
1) Неравенство (1) путем выделения полных квадратов сводится к условию
Т. е. описывает внутренность круга с центром А(9; -10) и радиусом R 1=√15 .
2) Неравенство (2) сводится к виду
Т. е. описывает внутренность круга с центром В(16; -6) и радиусом R 2=√21 .
Единственной точкой, принадлежащей одновременно двум кругам, будет точка М( 12; -8). Это выясняется подстановкой в систему числовых значений координат всех узлов квадратной сетки, соседних с точкой М.
Найти наименьшее значение суммы тогда 

Пусть искомое значение 
Угловой коэффициент равен -1, 
Треугольник ABC прямоугольный. Чтобы найти c , достаточно найти ординату точки B . Для этого найдем координаты точек A и B . Зная, что точки лежат на прямой с точкой O (1;-2), т. е. на прямой 

A ( 


Согласно рисунку 
B ( 

Ответ:
Видео:Решение диофантовых уравненийСкачать

4.Практическое применение теории диофантовых уравнений.
Неожиданно, лет 20-30 назад, было осознано, что эту чисто абстрактную теорию можно использовать для построения алгоритмов, которые нужны для криптографии, чтобы зашифровывать и безопасно передавать секретные сообщения, а также снимать и класть деньги в банкоматах и т. п. Теория эта оказалась востребована на практике. Яркий пример: в девяностые годы, когда математикам есть было нечего, многие уехали за границу, но многие и остались здесь, и некоторые математики из провинциальных институтов успешно сотрудничали с банками. Банкиры обратились к ним с просьбой помочь в переводе денег из дальних регионов в Москву. В России есть целая Академия криптографии и научно-исследовательские организации, которые используют такие разработки.
Знаменитый мост Золотые Ворота был построен с применением диофантовых уравнений.
Мост Золотые Ворота
Видео:РЕШАЕМ ДИОФАНТОВОЕ УРАВНЕНИЕ | ПРОСТЫМИ СЛОВАМИСкачать

Заключение.
В процессе исследования типов диофантовых уравнений мне удалось их классифицировать по способам решения, выработать алгоритм решения некоторых распространенных видов этих уравнений, научиться решать текстовые задачи, успешно справляться с заданиями части С ЕГЭ, о чем свидетельствует диплом 2 степени на всероссийской дистанционной олимпиаде по математике на сайте «Инфоурок. Ру.»
Данная исследовательская работа дала мне возможность совершенствовать навыки работы с научно-популярной литературой и освоить программы графопостроители.
Говоря о практическом использовании полученных результатов нельзя не вспомнить слова Алексея Николаевича Крылова: «Рано или поздно всякая правильная математическая идея находит применение в том или ином деле».
📺 Видео
Линейные диофантовы уравненияСкачать

Решите уравнение в целых числах 5x-4y=3 ➜ Как решать Диофантовы уравнения?Скачать

Диофантовы уравнения x+y=xyСкачать

#86. Делимость и диофантовы уравнения! ТРУДНАЯ ЗАДАЧА!Скачать

Алексей Савватеев "Диофантовы уравнения". Лекции 1-2Скачать

Глюоны: самые странные частицы в квантовой физикеСкачать

Диофантовы уравнения x³-y³=91Скачать

Диофантовы уравнения x²+xy-y=2Скачать

Решите уравнение в целых числах ★ √x+√y=√50 ★ Как решать диофантовы уравнения?Скачать

Решите уравнение в целых числах 3x^2+5y^2=345 ✱ Диофантовы уравнения ✱ Как решать?Скачать