Косинус угла между плоскостями через уравнения (5 видео)

Угол между плоскостями.

Содержание

Формула для вычисления угла между плоскостями
Примеры задач на вычисление угла между плоскостями
Угол между плоскостями. Онлайн калькулятор
Предупреждение
Угол между плоскостями − теория
Угол между плоскостями. Метод координат. Задание 14
🌟 Видео

Видео:Найти угол между плоскостямиСкачать

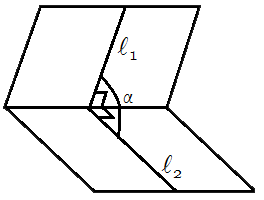
Формула для вычисления угла между плоскостями

Если заданы уравнения плоскостей A₁ x + B₁ y + C₁ z + D₁ = 0 и A₂ x + B₂ y + C₂ z + D₂ = 0, то угол между плоскостями можно найти, используя следующую формулу

cos α =	\|A₁·A₂ + B₁·B₂ + C₁·C₂\|
	√ A₁ 2 + B₁ 2 + C₁ 2 √ A₂ 2 + B₂ 2 + C₂ 2

Видео:Задание 1.13 Косинус угла между плоскостямиСкачать

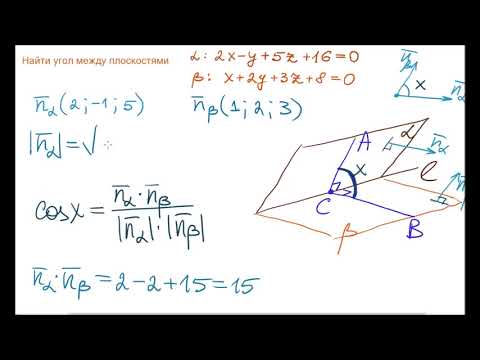
Примеры задач на вычисление угла между плоскостями

Решение. Подставим в формулу вычисления угла между плоскостями соответствующие коэффициенты:

cos α = |2·4 + 4·3 + (-4)·0| √ 2 2 + 4 2 + (-4) 2 √ 4 2 + 3 2 + 0 2 = |8 + 12| √ 36 √ 25 = 20 30 = 2 3

Ответ: косинус угла между плоскостями равен cos α = 2 3 .

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Видео:9. Угол между плоскостями Условия параллельности и перпендикулярности плоскостейСкачать

Угол между плоскостями. Онлайн калькулятор

С помощю этого онлайн калькулятора можно найти угол между плоскостями. Дается подробное решение с пояснениями. Для вычисления угла между плоскостями, введите элементы уравнения плоскостей в ячейки и нажимайте на кнопку «Решить».

Предупреждение

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Угол между плоскостями − теория

Пусть заданы две плоскости α и β общими уравнениями

A₁x+B₁y+C₁z+D₁=0,

(1)

A₂x+B₂y+C₂z+D₂=0

(2)

Из определения скалярного произведения, имеем

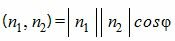Косинус угла между плоскостями через уравнения

(3)

Тогда из (3) можно найти косинус угла между нормальными векторами n₁ и n₂:

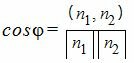(4)

Учитывая, что (n₁, n₂)=A₁A₂+B₁B₂+C₁C₂ и длины векторов |n₁|= и |n₂|=выражение (4) можно записать так:

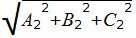
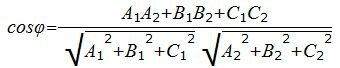(5)

Таким образом косинус угла между нормальными векторами и, следовательно, косинус угла между плоскостями α и β определяется формулой (5). Далее можно найти угол φ с помощью функции arccos.

Отметим, что пересекающиеся плоскости образую два угла. Другой угол можно найти так: φ‘=180−φ.

Видео:11 класс, 7 урок, Вычисление углов между прямыми и плоскостямиСкачать

Угол между плоскостями. Метод координат. Задание 14

Угол между плоскостями. Метод координант.

В этой статье я расскажу, как решать задачи на нахождение угла между плоскостями с помощью метода координат.

Сначала немного теории.

Две пересекающиеся плоскости образуют две пары равных между собой двугранных углов.

Величина двугранного угла измеряется величиной соответствующего линейного угла.

Чтобы построить линейный угол двугранного угла, нужно взять на линии пересечения плоскостей произвольную точку, и в каждой плоскости провести к этой точке луч перпендикулярно линии пересечения плоскостей. Угол, образованный этими лучами и есть линейный угол двугранного угла:

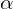
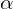
Пусть наши плоскости и заданы уравнениями:

Косинус угла между плоскостями находится по такой формуле:

В ответе мы записываем , так как величиной угла между плоскостями называется величина меньшего двугранного угла.

Решим задачу, которая была предложена на пробнике для подготовке к ЕГЭ 17 марта 2012 года.

В правильной четырехугольной призме со стороной основания 12 и высотой 21 на ребре взята точка М так, что . На ребре взята точка K так, что . Найдите угол между плоскостью и плоскостью .

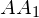
Сделаем чертеж. Так как мы будем использовать метод координат, сразу введем систему координат:

Теперь перед нами стоит задача написать уравнения плоскости и плоскости

Подробный алгоритм нахождения уравнения плоскости по трем точкам я описывала здесь.

После того, как мы найдем коэффициенты в уравнениях плоскости и плоскости , подставим их в формулу для нахождения косинуса угла между плоскостями, и найдем угол.