Корпускулярно волновой дуализм электрона уравнение э шредингера (2 видео)

Содержание

Корпускулярно волновой дуализм электрона уравнение э шредингера
Корпускулярно-волновой дуализм
Гипотеза де Бройля
Дифракция электронов
Соотношение неопределённостей
Корпускулярно волновой дуализм электрона уравнение э шредингера
📸 Видео

Видео:Волновая функция (видео 5) | Квантовая физика | ФизикаСкачать

Корпускулярно волновой дуализм электрона уравнение э шредингера

Элементы квантовой механики

Корпускулярно-волновой дуализм свойств частиц вещества.

§1 Волны де Бройля

В 1924г. Луи де Бройль (французский физик) пришел к выводу, что двойственность света должна быть распространена и на частицы вещества — электроны. Гипотеза де Бройля заключалась в том, что электрон, корпускулярные свойства которого (заряд, масса) изучаются давно, имеет еще и волновые свойства, т.е. при определенных условиях ведет себя как волна.

Количественные соотношения, связывающие корпускулярные и волновые свойства частиц, такие же, как для фотонов.

Идея де Бройля состояла в том, что это соотношение имеет универсальный характер, справедливый для любых волновых процессов. Любой частице, обладающей импульсом р, соответствует волна, длина которой вычисляется по формуле де Бройля.

— волна де Бройля

p = mv — импульс частицы, h — постоянная Планка.

Волны де Бройля , которые иногда называют электронными волнами, не являются электромагнитными.

В 1927 году Дэвиссон и Джермер ( амер. физик ) подтвердили гипотезу де Бройля обнаружив дифракцию электронов на кристалле никеля. Дифракционные максимумы соответствовали формуле Вульфа — Брэггов 2 dsin j = n l , а брэгговская длина волны оказалась в точности равной .

Дальнейшее подтверждение гипотезы де Бройля в опытах Л.С. Тартаковского и Г. Томсона, наблюдавших дифракционную картину при прохождении пучка быстрых электронов (Е » 50 кэВ) через фольгу из различных металлов. Затем была обнаружена дифракция нейтронов, протонов, атомных пучков и молекулярных пучков. Появились новые методы исследования вещества — нейтронография и электронография и возникла электронная оптика.

Макротела также должны обладать всеми свойствами ( m = 1кг, следовательно, l = 6 . 6 2 · 1 0 — 3 1 м — невозможно обнаружить современными методами — поэтому макротела рассматриваются только как корпускулы).

§2 Свойства волн де Бройля

Пусть частица массы m движется со скоростью v . Тогда фазовая скорость волн де Бройля

Т.к. c > v , то фазовая скорость волн де Бройля больше скорости света в вакууме ( v _ф может быть больше и может быть менше с, в отличие от групповой ).

следовательно, групповая скорость волн де Бройля равна скорости движения частицы.

т.е. групповая скорость равная скорости света.

Волны де Бройля испытывают дисперсию. Подставив в получим, что v_ф = f (λ). Из-за наличия дисперсии волны де Бройля нельзя представить в виде волнового пакета, т.к. он мгновенно “ расплывется “ (исчезнет) за время 10 -26 с.

§3 Соотношение неопределенностей Гейзенберга

Микрочастицы в одних случаях проявляют себя как волны, в других как корпускулы. К ним не применимы законы классической физики частиц и волн. В квантовой физике доказывается, что к микрочастице нельзя применять понятие траектории, но можно сказать, что частица находится в данном объеме пространства с некоторой вероятностью Р. Уменьшая объем, мы будем уменьшать вероятность обнаружить частицу в нем. Вероятностное описание траектории (или положения) частицы приводит к тому, что импульс и, следовательно, скорость частицы может быть определена с какой-то определенной точностью.

Далее, нельзя говорить о длине волны в данной точке пространства и отсюда следует, что если мы точно задаем координату Х, то мы ничего не сможем сказать о импульсе частицы, т.к. . Только рассматривая протяженный участок D C мы сможем определить импульс частицы. Чем больше D C , тем точнее D р и наоборот, чем меньше D C , тем больше неопределенность в нахождении D р .

Соотношение неопределенностей Гейзенберга устанавливает границу в одновременном определении точности канонически сопряженных величин, к которым относятся координата и импульс, энергия и время.

Соотношение неопределенностей Гейзенберга: произведение неопределенностей значений двух сопряженных величин не может быть по порядку величины меньше постоянной Планка h

( иногда записывают )

Таким образом. для микрочастицы не существует состояний, в которых её координата и импульс имели бы одновременно точные значения. Чем меньше неопределенность одной величины, тем больше неопределенность другой.

Соотношение неопределенностей является квантовым ограничением применимости классической механики к микрообъектам.

следовательно, чем больше m , тем меньше неопределенности в определении координаты и скорости. При m = 10 -12 кг , ? = 10 -6 и Δ x = 1% ?, Δv = 6,62·10 -14 м/с, т.е. не будет сказываться при всех скоростях, с которыми пылинки могут двигаться, т.е. для макротел их волновые свойства не играют никакой роли.

Пусть электрон движется в атоме водорода. Допустим Δ x » 1 0 -10 м (порядка размеров атома, т.е. электрон принадлежит данному атому). Тогда

Δv = 7,27· 1 0 6 м/с. По классической механике при движении по радиусу r » 0 , 5 · 1 0 — 1 0 м v = 2,3·10 -6 м/с. Т.е. неопределенность скорости на порядок больше величины скорости, следовательно, нельзя применять законы классической механики к микромиру.

Из соотношения следует, что система имеющая время жизни D t , не может быть охарактеризована определенным значением энергии. Разброс энергии возрастает с уменьшением среднего времени жизни. Следовательно, частота излученного фотона также должна иметь неопределенность D n = D E / h , т.е. спектральные линии будут иметь некоторую ширину n ± D E / h , будут размыты. Измерив ширину спектральной линии можно оценить порядок времени существования атома в возбужденном состоянии.

§4 Волновая функция и ее физический смысл

Дифракционная картина, наблюдающаяся для микрочастиц, характеризуется неодинаковым распределением потоков микрочастиц в различных направлениях — имеются минимумы и максимумы в других направлениях. Наличие максимумов в дифракционной картине означает, что в этих направлениях распределяются волны де Бройля с наибольшей интенсивностью. А интенсивность будет максимальной, если в этом направлении распространяется максимальное число частиц. Т.е. дифракционная картина для микрочастиц является проявлением статистической (вероятностной) закономерности в распределении частиц: где интенсивность волны де Бройля максимальная, там и частиц больше.

Волны де Бройля в квантовой механике рассматриваются как волны вероятности, т.е. вероятность обнаружить частицу в различных точках пространства меняется по волновому закону ( т.е.

е — iωt ). Но для некоторых точек пространства такая вероятность будет отрицательной (т.е. частица не попадает в эту область). М. Борн ( немецкий физик ) предположил, что по волновому закону меняется не сама вероятность, а амплитуда вероятности, которую также называют волновой функцией или y -функцией (пси — функцией).

Волновая функция — функция координат и времени.

Квадрат модуля пси-функции определяет вероятность того, что частица будет обнаружена в пределах объема dV — физический смысл имеет не сама пси-функция, а квадрат ее модуля.

Ψ * — функция комплексно сопряженная с Ψ

Если частица находится в конечном объеме V , то возможность обнаружить ее в этом объеме равна 1, (достоверное событие)

Р = 1 Þ

В квантовой механике принимается, что Ψ и АΨ, где А = const , описывают одно и то же состояние частицы. Следовательно,

интеграл по , означает, что он вычисляется по безграничному объему (пронстранству).

y — функция должна быть

1) конечной (так как Р не может быть больше1),

2) однозначной (нельзя обнаружить частицу при неизменных условиях с вероятностью допустим 0,01 и 0,9, так как вероятность должна быть однозначной).

непрерывной (следует из неприрывности пространства. Всегда имеется вероятность обнаружить частицу в разных точках пространства, но для разных точек она будет разная),
Волновая функция удовлетворяет принципусуперпозиции: если система может находится в различных состояниях, описываемых волновыми функциями y ₁ , y ₂ . y _n , то она может находится в состоянии y , описываемой линейной комбинаций этих функций:

С _n ( n =1,2. ) — любые числа.

С помощью волновой функции вычисляются средние значения любой физической величины частицы

§5 Уравнение Шредингера

Уравнение Шредингера, как и другие основные уравнения физики (уравнения Ньютона, Максвелла), не выводится, а постулируется. Его следует рассматривать как исходное основное предположение, справедливость которого доказывается тем, что все вытекающие из него следствия точно согласуются с экспериментальными данными.

(1)

— Временное уравнение Шредингера.

— набла — оператор Лапласа

— потенциальная функция частицы в силовом поле,

Ψ( y , z , t ) — искомая функция

Если силовое поле, в котором движется частица, стационарно (т.е. не изменяется с течением времени), то функция U не зависит от времени и имеет смысл потенциальной энергии. В этом случае решение уравнения Шредингера (т.е. Ψ — функция) может быть представлено в виде произведения двух сомножителей — один зависит только от координат, другой — только от времени:

(2)

Е — полная энергия частицы, постоянная в случае стационарного поля.

(3)

— Уравнение Шредингера для стационарных состояний.

Имеется бесконечно много решений. Посредством наложения граничных условий отбирают решения, имеющие физический смысл.

волновые функции должны быть регулярными, т.е.

Решения, удовлетворяющие уравнению Шредингера, называются собственными функциями, а соответствующие им значения энергии — собственными значениями энергии. Совокупность собственных значений называется спектром величины. Если Е _n принимает дискретные значения, то спектр — дискретный, если непрерывные — сплошной или непрерывный.

§6 Движение свободной частицы

Частица называется свободной, если на нее не действуют силовые поля, т.е. U = 0.

Уравнение Шредингера для стационарных состояний в этом случае:

И собственные значения энергии:

Т.к. k может принимать любые значения, то, следовательно, и Е принимает любые значения, т.е. энергетический спектр будет сплошным.

Временная волновая функция

(- уравнение волны)

т.е. представляет плоскую монохромную волну де Бройля.

§7 Частица в “потенциальной яме” прямоугольной формы.

Квантование энергии.

Найдем собственные значения энергии и соответствующие им собственные функции для частицы, находящейся в бесконечно глубокой одномерной потенциальной яме. Предположим что, частица может двигаться только вдоль оси x . Пусть движение ограничено непроницаемыми для частицы стенками x = 0, и x = ?. Потенциальная энергия U имеет вид:

Уравнение Шредингера для стационарных состояний для одномерной задачи

За пределы потенциальной ямы частица попасть не сможет, поэтому вероятность обнаружения частицы вне ямы равна 0.Следовательно, и Ψ за пределами ямы равна 0 .Из условий непрерывности следует, что Ψ = 0 и на границах ямы т.е.

В пределах ямы (0 £ x £ l ) U = 0 и уравнение Шредингера.

введя получим

;

из граничных условий следует

Из граничного условия

Энергия Е _n частицы в «потенциальной яме» с бесконечно высокими стенками принимает лишь определенные дискретные значения, т.е. квантуется. Квантованные значения энергии Е _n называются уровнями энергии, а число n , определяющее энергические уровни частицы, называется главным квантовым числом. Т.е. частицы в «потенциальной яме» могут находиться только на определенном энергетическом уровне Е _n (или находятся в квантовом состоянии n )

Собственные функции:

А найдем из усилия нормировки

— плотность вероятности. Из рис. видно, что плотность вероятности меняется в зависимости от n : при n = 1 частица, скорее всего, будет посередине ямы, но не на краях, при n = 2 — будет или в левой или в правой половине, но не посередине ямы и не на краях, и т.д. Т.е нельзя говорить о траектории движения частицы.

Энергетический интервал между соседними уровнями энергии:

При n = 1 имеет наименьшую энергию отличную от нуля

Наличие минимума энергии следует из соотношения неопределенностей, т.к.,

C ростом n расстояние между уровнями уменьшается и при n ® ¥ Е _n практически непрерывны, т.е. дискретность сглаживается, т.е. выполняется принцип соответствия Бора: при больших значениях квантовых чисел законы квантовой механики переходят в законы классической физики.

Общая трактовка принципа соответствия: всякая новая, более общая теория является развитием классической, не отвергает ее полностью, а включает в себя классическую, указывая границы её применимости.

§ 8 Туннельный эффект.

Прохождение частицы через потенциальный барьер

Для классической частицы : при Е > U она пройдет над барьером, при Е U — отразится от него; для квантовой : при Е > U есть вероятность того, что частица отразится, при Е U есть вероятность того, что пройдет сквозь барьер.

Потенциальная энергия:

Уравнение Шредингера: для области 1 и 3 :

для области 2:

Решение этих диф. уравнений;

Для 1;

Для 2;

Для 3:

Т.к. в области 3 возможно распределение только прошедшей волны, то, Þ , В₃=0.

В области 2 решение зависит от соотношений Е > U или Е U . Физический интерес представляет случай Е U .

q = i b , где

Тогда решение уравнения Шредингера запишутся в виде:

Для 1;

Для 2;

Для 3:

Качественный вид функций показан на рис. 2. Из рис. 2 видно, что функция не равна нулю внутри барьера, а в 3 имеет вид волны де Бройля, если барьер не очень широк.

Явление “проникновения” частицы сквозь потенциальный барьер, называется туннельным эффектом. Туннельный эффект является специфическим квантовым эффектом. Прохождение частицы можно объяснить используя соотношения неопределенностей: неопределенность импульса D р на отрезке D x = ? составляет . Связанная с этим разбросом в значениях импульса кинетическая энергия может оказаться достаточной для того, чтобы полная энергия частицы оказалась больше потенциальной энергии барьера.

§9 Линейный гармонический осциллятор

Линейный гармонический осциллятор — система, совершающая одномерное колебательное движение под действием квазиупругой силы — является моделью для изучения колебательного движения.

В классической физике — это пружинный, физический и математический маятники. В квантовой физике — квантовый осциллятор.

Записав потенциальную энергию в виде

Уравнение Шредингера запишется в виде:

Тогда собственные значения энергии:

т.е. энергия квантового осциллятора принимает дискретные значения, т.е. квантуется. Минимальное значение — энергия нулевых колебаний — является следствием состояния неопределенности так же, как и в случае частицы в “потенциальной яме”.

Наличие нулевых колебаний означает, что частицы не могут упасть на дно ямы, т.к. в этом случае был бы точно определен ее импульс p = 0, D p = 0, Þ , D x = ¥ — не соответствует соотношению неопределенностей. Наличие энергии нулевых колебаний противоречит классическим представлениям, по которым E _min = 0. — уровни энергии расположенные на равных расстояниях друг от друга. Из квантового рассмотрения следует, что частицу можно обнаружить вне области. По классическому рассмотрению только в пределах – x £ x £ x (Рис.2).

Видео:Волна де Бройля (видео 4) | Квантовая физика | ФизикаСкачать

Корпускулярно-волновой дуализм

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: гипотеза де Бройля о волновых свойствах частиц, корпускулярно-волновой дуализм, дифракция электронов.

Корпускулярно-волновой дуализм (слово дуализм означает двойственность) — это физический принцип, утверждающий, что любой объект природы может вести себя и как частица, и как волна.

С первым проявлением этого принципа мы столкнулись в предыдущем листке, когда говорили о двойственной, корпускулярно-волновой природе света. В явлениях интерференции и дифракции свет демонстрирует свою волновую природу. В явлении фотоэффекта свет выступает как дискретный поток частиц — фотонов.

Является ли свет каким-то особым объектом нашего мира, таким, что подобный дуализм присущ только ему? Или, быть может, корпускулярно-волновой дуализм — это свойство вообще всех материальных объектов, просто впервые обнаружен он был для света?

Видео:Урок 450. Корпускулярно-волновой дуализм. Гипотеза де БройляСкачать

Гипотеза де Бройля

Идея об универсальной двойственности корпускулярных и волновых свойств всех объектов природы была впервые высказана Луи де Бройлем (в 1924году) в качестве гипотезы о волновых свойствах частиц.

Итак, мы знаем, что свету с частотой и длиной волны соответствуют частицы — фотоны, обладающие энергией и импульсом . Де Бройль, в сущности, постулировал обратное.

Гипотеза де Бройля. Движению каждой частицы соответствует распространение некоторой волны. Частота и длина этой волны определяются энергией и импульсом частицы:

Точно так же, любой волне с частотой и длиной волны отвечают частицы с энергией и импульсом .

Чтобы лучше осмыслить гипотезу де Бройля, давайте обсудим дуализм «волна–частица» на примере электромагнитного излучения.

В случае электромагнитных волн мы имеем следующую закономерность. По мере увеличения длины волны всё легче наблюдать волновые свойства излучения и всё труднее — корпускулярные. И наоборот, чем меньше длина волны, тем ярче выражены корпускулярные свойства излучения и тем труднее наблюдать его волновые свойства. Изменение соотношения корпускулярных и волновых свойств хорошо прослеживается при движении по известной вам шкале электромагнитных волн.

• Радиоволны.Длины волн здесь настолько велики, что корпускулярные свойства излучения практически не проявляются. Волновые свойства в этом диапазоне абсолютно доминируют.

Длины волн могут составлять несколько метров или даже километров, так что волновая природа проявляется «сама собой» — радиоволны в процессе дифракции запросто огибают дома или горы. Излучение радиоволн и их взаимодействие с материальными объектами отлично описывается в рамках классической электродинамики.

• Видимый свет и ультрафиолет. Это своего рода «переходная область»: в оптике мы можем наблюдать как волновые свойства света, так и корпускулярные.

Однако в обоих случаях надо постараться. Так, длины волн видимого света много меньше размеров окружающих нас тел, поэтому в опытах по интерференции или дифракции света нужно создавать специальные условия (малость щелей или отверстий, удалённость экрана). В свою очередь, термин «красная граница фотоэффекта» также подчёркивает пограничность данного диапазона: фотоэффект начинается лишь при переходе через красную границу.

• Рентгеновское и гамма-излучение. Длины волн очень малы, и наблюдать волновые свойства излучения весьма затруднительно. Так, верхняя граница длин волн рентгеновского излучения составляет нм; это лишь на два порядка превышает размер атома. Ясно, что дифракцию на «обычных» препятствиях при такой длине волны наблюдать невозможно.

Однако в рентгеновский диапазон входят длины волн порядка размера атома и межатомных расстояний в кристалле ( нм). Поэтому дифракция рентгеновских лучей наблюдается на «естественных» дифракционных решётках — кристаллических решётках твёрдых тел (эта идея была высказана немецким физиком Лауэ в 1912 году).

Энергия квантов в рентгеновском и гамма-диапазоне настолько велика, что излучение ведёт себя почти стопроцентно как поток частиц.

Рассуждая по аналогии с электромагнитными волнами, можно заключить, что и частица будет проявлять волновые свойства тем лучше, чем больше её длина волны де Бройля (в масштабах данной ситуации).

Так, мы совсем не наблюдаем волновых свойств у окружающих нас тел. (Видели вы, например, интерференцию движущихся автомобилей?) А почему? Давайте посчитаем длину дебройлевской волны объекта массой кг, движущегося со скоростью м/с:

Это на порядков меньше размера атома. Воображение отказывается представить себе столь малую величину. Разумеется, никакого волнового поведения у нашего объекта при таких условиях не обнаруживается — он стопроцентно ведёт себя как «частица», то есть как материальная точка классической механики.

Видео:Теория Бора. Гипотеза де Бройля. Принцип неопределенности. Уравнение Шрёдингера.Скачать

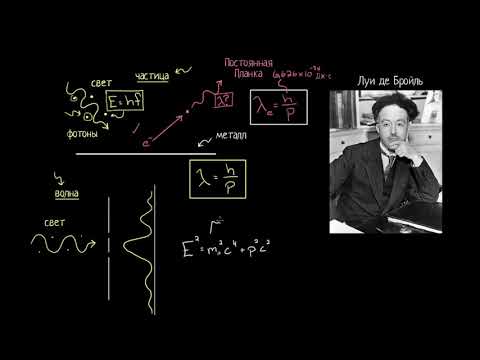
Дифракция электронов

Совсем другое дело — электрон. Масса электрона равна кг, и столь малое значение массы (а стало быть, и импульса в формуле ) может дать длину волны де Бройля, достаточную для экспериментального обнаружения волновых свойств.

И вот оказывается, что электроны с энергией эВ (при такой энергии становится несущественным хаотическое тепловое движение электронов, и электронный пучок можно считать когерентным) имеют дебройлевскую длину волны примерно нм — это как раз порядка размера атома и расстояний между атомами в кристаллической решётке! Опыт по наблюдению дифракции рентгеновских лучей на кристаллических структурах уже имелся, поэтому оставалось направить на кристаллическую решётку пучок электронов.

Впервые это было сделано в знаменитом эксперименте американских физиков Дэвиссона и Джермера (1927 год). Дифракция электронов на кристаллах была обнаружена! Как и ожидалось, полученная дифракционная картина имела тот же характер, что и при дифракции на кристаллической решётке рентгеновских лучей.

Впоследствии волновые свойства были обнаружены и у более крупных частиц: протонов, нейтронов, атомов и молекул. Гипотеза де Бройля, таким образом, получила надёжное опытное подтверждение.

Видео:Естествознание 10 класс (Урок№14 - Корпускулярно-волновой дуализм.)Скачать

Соотношение неопределённостей

Обнаружение корпускулярных свойств электромагнитных волн и волновых свойств частиц показало, что объекты микромира подчиняются необычным законам. Эти законы совершенно непривычны для нас, привыкших наблюдать за макроскопическими телами.

Наше сознание выработало некоторые образы частицы и волны, вполне пригодные для описания объектов классической физики. Частица — это маленький, локализованный в пространстве сгусток вещества. Волна — это распределённый (не локализованный) в пространстве колебательный процесс. Как же эти понятия могут совмещаться в одном объекте (например, в электроне)?

Вообразить такое действительно получается с трудом. Но что поделать — это факт. Природа оказывается намного богаче нашего воображения. В своей повседневной жизни мы находимся очень далеко от микромира, и в привычном нам диапазоне макроскопических тел природа демонстрирует свои «крайние» проявления — в виде «только частиц» или «только волн». Вот почему корпускулярные и волновые свойства представляются нам несовместимыми друг с другом. Но на самом деле это не так: в микромире оказывается, что один и тот же объект (например, электрон) легко может обладать обоими свойствами одновременно — словно человек, обладающий разными, несовместимыми на первый взгляд чертами характера.

Так, будучи частицей, электрон локализован в пространстве; но, будучи волной, локализован не в точке, а «размазан» по некоторой области. Координаты и скорость электрона не могут быть измерены одновременно сколь угодно точно. Неопределённость координаты и неопределённость соответствующей проекции импульса оказываются связанными соотношением неопределённостей Гейзенберга:

Соотношение неопределённостей (2) имеет фундаментальный характер — оно применимо к любым объектам природы. Чем точнее мы знаем координаты объекта (то есть чем в меньшей пространственной области он локализован), тем больше получается разброс значений его импульса(то есть тем с большей скоростью объект «готов вылететь» из этой области). И наоборот, чем точнее мы знаем импульс объекта, тем меньше у нас информации о том, где этот объект находится.

Но коль скоро нет возможности одновременно точно измерить координаты и скорость, то теряет смысл понятие траектории движения объекта. Механика Ньютона перестаёт работать в микромире и уступает место квантовой механике.

Видео:В чем парадокс ЭФФЕКТА НАБЛЮДАТЕЛЯ? | Кот Шрёдингера и параллельные мирыСкачать

Корпускулярно волновой дуализм электрона уравнение э шредингера

Корпускулярно-волновой дуализм. Уравнение Шрёдингера
План

Экспериментальное обоснование основных идей квантовой теории
1. Коротковолновая граница сплошного рентгеновского спектра
2. Опыт Боте
Связь между волновой и корпускулярной картинами
Гипотеза де Бройля
Микрочастица в двухлучевом интерферометре
Соотношение неопределённостей
Волновая функция, её вероятностная интерпретация и свойства
Уравнение Шрёдингера
1. Нестационарное (временное) уравнение Шрёдингера
2. Стационарное уравнение Шрёдингера
3. Собственные функции, собственные значения
Применение уравнения Шрёдингера
1. Одномерное движение свободной частицы
2. Частица в одномерной потенциальной яме с бесконечно высокими стенками
3. Линейный гармонический осциллятор

а) Классический

1. Экспериментальное обоснование основных идей квантовой теории

Волновые свойства света проявляются в явлениях:

интерференции,
дифракции,
поляризации.

Явления:

фотоэффекта,
комптоновского рассеяния,
тепловое излучение

могут быть объяснены только корпускулярными свойствами.

Давление света можно объяснить и с точки зрения волновой, и корпускулярной теории.

К экспериментальному обоснованию квантовых свойств относятся:

существование коротковолновой границы сплошного рентгеновского спектра;
опыт Боте.

1.1. Коротковолновая граница сплошного рентгеновского спектра

R-лучи получают в рентгеновской трубке (рис.21.1): катод К, нагретый проходящим через него током, испускает электроны в результате термоэлектронной эмиссии. Электроны разгоняются между катодом и анодом (антикатодом) А в вакуумированной трубке ускоряющим напряжением U порядка нескольких десятков киловольт. Попадая в толщу массивного антикатода, электроны резко тормозятся, то есть движутся ускоренно, следовательно, излучают электромагнитные волны, — это и есть тормозное рентгеновское излучение. Оно имеет сплошной спектр, резко ограниченный со стороны коротких волн (рис.21.2). С увеличением напряжения U длина волны коротковолновой границы уменьшается, а при достаточно большом значении U возникают резкие интенсивные линии характеристического излучения. О причинах возникновения характеристического излучения пока говорить не будем. Что касается тормозного излучения, то максимальная энергия фотона равна энергии электрона, ускоренного напряжением U и теряемой электроном при торможении:

, (21.1)

,
Рис.21.2

. (21.2)

Не привлекая гипотезу о квантах излучения с энергией

, (21.3)

не удаётся объяснить существование коротковолновой границы тормозного спектра.

Этот опыт должен был дать ответ на вопрос, как же происходит электромагнитное излучение: как волна или как поток дискретных частиц – фотонов.

М
еталлическая фольга облучается рентгеновским излучением и сама, в свою очередь, становится источником рентгеновского излучения (рис.21.3). Счётчики Гейгера, расположенные симметрично, фиксируют вторичные R-лучи. Если бы вторичное излучение распространялось в виде сферических волн, оба счётчика должны срабатывать одновременно, и на ленте самописца отметки слева и справа совпадали бы. Опыт дал другие результаты: счётчики срабатывали случайным образом, неодновременно. Это значит, что при излучении возникали отдельные фотоны, попадавшие либо в один счётчик, либо в другой.

2. Связь между волновой и корпускулярной картинами

Таким образом, оказалось, что свет обнаруживает корпускулярно-волновой дуализм: обладает и свойствами волн, и свойствами частиц. Эти свойства с макроскопической точки зрения противоречат друг другу: волна непрерывна, частица – дискретна; волна – безгранична, частица – ограничена в пространстве. Как совместить эти противоречащие друг другу свойства? Эта задача была решена. Установить связь между волновой и корпускулярной картинами можно с помощью статистического подхода.

Запишем уравнение электромагнитной волны (Е – напряжённость электрического поля волны; Е₀ – амплитуда):

. (21.4)

Тогда вероятность dp того, что фотон будет обнаружен в малом объёме вблизи точки с радиус-вектором (или координатами x,y,z), пропорциональна – квадрату амплитуды волны и объёму :

, (21.5)

Здесь – некоторый коэффициент пропорциональности.

Таким образом, распределение фотонов носит статистический характер. Квадрат амплитуды волны определяет вероятность попадания фотона в данную точку.
3. Гипотеза де Бройля

В 1923 г. Луи де Бройль выдвинул гипотезу, что корпускулярно-волновой дуализм универсален, то есть частицы обладают волновыми свойствами. Существует симметрия: если свет (волна) обладает корпускулярными свойствами, то почему бы частицам не проявлять свойства волновые? Природа едина.

Короче, всем частицам (фотонам, протонам, электронам, нейтронам, атомам, молекулам,…) приписываем

корпускулярные свойства (энергию и импульс ) и
волновые свойства (длину волны и частоту ).

При этом длина волны связана с импульсом для любой частицы так же, как и для фотона (см. лекцию № 20):

. (21.6)

Это – длина волны де Бройля.

Для любой частицы справедливы соотношения:

Корпускулярные свойства	Волновые свойства

Движущейся частице с импульсом и энергией сопоставлена волна:

; (21.7)

Для волны, бегущей вдоль оси OX (частицы, движущейся параллельно оси OX):

. (21.8)

(Смысл функции пока прояснять не будем.)

Подтверждение гипотезы де Бройля было получено экспериментально (1927 год) при наблюдении дифракции электронов:

Опыты Дэвиссона и Джермера. Отражение электронов от кристалла никеля подчиняется формуле Брэгга-Вульфа (см. лекцию № 18):

. (21.9)

В опытах Дж.Томсона исследовалась дифракция электронов на тонкой металлической поликристаллической фольге (рис.21.4). На фотопластинке появлялась дифракционная картина в виде концентрических колец, опять же в соответствии с формулой Брэгга-Вульфа.

Электроны, ускоренные в электрическом поле разностью потенциалов U, имеют энергию

Тогда длина волны де Бройля

. (21.10)

Совпадение длин волн, предсказанных де Бройлем по (21.10) и полученных из эксперимента по (21.9), совпали с точностью до 1%. Волновые свойства электрона обнаружились и в других экспериментах. Более того, удалось наблюдать дифракцию нейтронов на кристаллах (1936 год), а также атомов (гелий) и молекул (водород). Есть эксперименты по дифракции больших молекул красителя фталоцианина на специально созданной дифракционной решётке (рис.21.5).

Замечательно, что волновые свойства присущи каждой частице: дифракционная картина наблюдается и в случае очень слабых пучков, когда частицы летят поодиночке. На рис.21.6 (а, б, в, г) видно, как со временем по мере выпуска всё новых и новых молекул на финальной пластине всё ярче и ярче проступает интерференционная картина. Благодаря дифракции случайно прибывающие на финиш массивные частицы проявляют свои волновые свойства.

4. Микрочастица в двухщелевом интерферометре

И
ллюстрацией двойственности свойств микрочастиц является опыт с двухщелевым интерферометром. Диафрагма с двумя щелями обстреливается потоком микрочастиц (электронов), которые затем попадают на экран (рис.21.7, а). Если открыта одна щель, напротив неё на экране получается полоса (рис.21.7,а). Открывая вторую щель, ожидаем получить на экране две полосы, то есть простое сложение картинок при одной и второй открытой щелях (рис.21.7,б), как это было бы в макромире при обстреле диафрагмы с щелями обычными пулями. Но в опытах микрочастицами на экране появляется типичная интерференционная картина (рис.21.8), характерная для световых волн в аналогичном опыте Юнга. Электроны интерферируют при прохождении через две щели.

Пули дискретны, неделимы: каждая проходит через какую-то одну из двух щелей; никакой интерференции нет.
Электрон, как и пуля, дискретен, он не может разделиться и пройти одновременно через обе щели. Проделаем тот же эксперимент с волнами (рис.21.9): волна проходит через обе щели, она непрерывна. Для волн нет дискретности; есть интерференция.

Электроны (и любые микрочастицы) дискретны, как пули, но испытывают интерференцию, как волны.

Могло создаться впечатление, что микрочастицы интерферируют, потому что взаимодействуют друг с другом. Но даже для очень слабых пучков, когда микрочастицы летят поодиночке, интерференционная картина рис. 21.8, б, сохранялась, только нужно было подождать достаточно долго, чтобы картина достаточно проявилась. Электроны как будто «знают», что открыты обе щели, и попадают в нужные места экрана: туда, где должны быть интерференционные максимумы. Электрон интерферирует сам с собой? На движение одиночного, дискретного и неделимого электрона оказывают влияние обе щели.

Как это понять? Приходится принять, что микрочастица обладает принципиально иными свойствами, чем макрочастица. У микрочастиц нет траектории.

Электрон не может «разделиться» на половинки и пролететь сразу через обе щели. Всё-таки хотелось бы знать, через какую щель пролетел электрон. «Подсмотрим» за электроном, поставив сразу за каждой из щелей источник света. Электрон, прошедший через данную щель, будет рассеивать свет, и мы это «увидим», то есть будем точно знать, через какую из щелей прошёл электрон; а если он, разделившись, пройдёт сразу через две щели, вспышки у каждой из щелей произойдут одновременно. В этом эксперименте получили, что электрон проходит только либо через одну щель, либо только через вторую. Но при этом никакой интерференции нет (рис.21.10). Выключаем источники света, и картинка интерференции появляется снова (рис. 21.8, б).

Если не знаем координату (неизвестно, через какую щель пролетела микрочастица), то интерференция есть; тогда знаем длину волны де Бройля, знаем импульс частицы:

Если будем фиксировать, через какую щель прошёл электрон (включили лампочку), то не получим интерференции. Если знаем координату электрона (пролетел через данную щель), то не знаем длину волны, не знаем импульс.

5. Соотношение неопределённостей

Из корпускулярно-волнового дуализма микрочастиц вытекает, что нельзя одновременно точно знать её координату и импульс. Нельзя сказать: длина волны в данной точке; волна – протяжённый в пространстве объект. Если точно знаем импульс частицы, то знаем длину волны де Бройля (21.6):

можем записать волновое уравнение (21.7), но совершенно не знаем, где находится наша частица: гармоническая волна в пространстве бесконечна.

В 1927 году подобные соображения были сформулированы Гейзенбергом в виде принципа неопределённостей:

Произведение неопределённостей координаты и соответствующей проекции импульса частицы не меньше ():

. (21.11)

Аналогично, для осей OY и OZ:

;

Существуют пары физических величин, которые, подобно импульсу и координате, нельзя измерять одновременно точно. Такие величины называются сопряжёнными динамическими переменными. Это время и энергия; момент импульса и угловая координата. Запишем принцип неопределённостей для таких сопряжённых величин:

; (21.11а)

. (21.11б)

Здесь – неопределённость энергии, – неопределённость момента измерения энергии.

Принцип неопределённостей Гейзенберга не связан с несовершенством приборов или методов измерения; является спецификой микрочастиц – проявлением корпускулярно-волнового дуализма.
6. Волновая функция, её вероятностная интерпретация и свойства

Квантовая механика была создана в начале 20-го века. В ней учитываются волновые свойства микрочастиц. Авторы квантовой механики: Планк, Гейзенберг, Шрёдингер, Борн.

Состояние микрообъекта в квантовой механике описывается волновой функцией (пси-функция) . В общем случае это – функция координат и времени; а значения функции – комплексные.

Смысл функции: квадрат модуля волновой функции определяет вероятность нахождения частицы в данной точке, то есть вероятность dp обнаружить частицу в объёме dV вблизи заданной точки с координатами x, y, z в момент времени t равна

. (21.12)

, (21.12а)

где – комплексно сопряжённая функция.

Плотность вероятности обнаружения частицы в данной точке равна квадрату модуля волновой функции:

. (21.13)
Свойства волновой функции:

Однозначна, конечна, непрерывна, дифференцируема.
Вероятность p_V найти частицу в конечном объёме V равна (из (21.12)):

. (21.14)

Вероятность найти частицу хотя бы где-нибудь: неважно, в какой точке пространства – достоверное событие (если частица существует); поэтому сумма всех вероятностей по всему пространству есть единица:

. (21.15)

Это – условие нормировки. Уточнение: интеграл в (21.15) берётся по всей области определения функции.

Волновую функцию можно домножить на любое комплексное число С, и полученная функция будет описывать то же самое состояние: и описывают одинаковые состояния частицы.
Если частица может находиться в состоянии, описываемом функциями , или , …, или , то возможно состояние частицы, описываемое любой линейной комбинацией этих функций:

, (21.16)

где – комплексные числа. Это свойство называется принципом суперпозиции. Именно оно легло в основу экспериментов по квантовой телепортации.

Зная волновую функцию состояния, можно найти среднее значение любой физической величины В:

. (21.17)

Описание состояния частицы с помощью волновой функции не позволяет найти ни координаты частицы, ни её траекторию. Однако утверждается, что волновая функция даёт исчерпывающее описание поведения микрочастицы. Волновая функция не даёт информации о том, чего нет: у микрочастиц нет траектории, нет точных значений координат в любой момент времени.

7. Уравнение Шрёдингера

7.1. Нестационарное (временное) уравнение Шрёдингера

Уравнение Шрёдингера – основное уравнение квантовой механики. Оно получено в 1926 году. Решением уравнения Шрёдингера получают волновую функцию состояния . Уравнение не доказывается теоретически и не может быть выведено из других соотношений. Можно сказать, что уравнение Шрёдингера – постулат квантовой механики, аналогично законам Ньютона в классической механике. Законы Ньютона – обобщение большого количества опытных данных. С уравнением Шрёдингера немножко сложнее: справедливость его доказывается тем, что следствия из него согласуются с опытом.

Временное уравнение Шрёдингера:

. (21.18)

Здесь – функция координат и времени (поэтому уравнение – временное); i – мнимая единица ();– оператор Лапласа:

; (21.19)

;

– потенциальная функция частицы. Если зависит только от координат, но не зависит от времени, то это – потенциальная энергия частицы.
7.2. Стационарное уравнение Шрёдингера

Оказывается, что если не зависит от времени, то полную волновую функцию можно представить в виде произведения координатной и временной частей , зависящих только от координат или только от времени соответственно:

. (21.20)

, (21.21)

поскольку временная часть не зависит от координат, а в оператор Лапласа входят только частные производные по координатам. Далее,

. (21.22)

Подставляем (21.21) и (21.22) во временное уравнение Шрёдингера (21.18) и сокращаем на :

;

Полная энергия частицы по (21.7) ; ; тогда

;

. (21.23)

Это – стационарное уравнение Шрёдингера.

7.3. Собственные функции, собственные значения

Решение уравнения Шрёдингера существует не для любых значений энергии Е. Значения энергии, при которых решение существует, называются собственными значениями. Соответствующие им волновые функции тоже называются собственными функциями.

Совокупность собственных значений энергии – спектр (энергетический спектр). Спектр энергии может быть дискретным (набор конкретных значений) или непрерывным, сплошным. Если спектр дискретный, собственные значения можно пронумеровать:

, , ,…,…

Этим значениям соответствуют собственные функции:

Возможен вариант, когда одному и тому же собственному значению энергии соответствует несколько волновых функций; например, три:

Тогда соответствующий уровень энергии называется вырожденным, причём кратность вырождения равна числу волновых функций. В приведённом примере уровень трижды вырожден.

Замечание: Квантование энергии при решении уравнения Шрёдингера получается естественно, без привлечения каких-либо дополнительных соображений.
8. Применение уравнения Шрёдингера

8.1. Одномерное движение свободной частицы

Пусть частица движется в постоянном потенциальном поле, причём потенциальная энергия частицы меньше её полной энергии:

Рассматривается одномерное движение вдоль оси OX, тогда волновая функция зависит только от координаты x (), и стационарное уравнение Шрёдингера (21.23) примет вид:

;

Это обыкновенное дифференциальное однородное уравнение второго порядка; его решением, в частности, будет гармоническая функция:

Здесь – волновое число; .

Запишем общее решение, помня, что волновая функция – комплексная:

;

Получили суперпозицию двух волн: первое слагаемое представляет собой волну, бегущую в положительном направлении оси OX, второе – в отрицательном.

Действительная часть пси-функции – это суперпозиция двух косинусов (по формуле Эйлера ):

.
8.2. Частица в одномерной потенциальной яме с бесконечно высокими стенками

Рассмотрим частицу в одномерной потенциальной яме шириной l с бесконечно высокими стенками, то есть потенциальная энергия частицы U обращается в бесконечность при и и равна нулю при (рис.21.11). Найдём возможные значения энергии частицы в таком потенциальном поле и соответствующие волновые функции.

За пределы потенциальной ямы частица выйти не может, так как там . Следовательно, волновая функция равна нулю при и , а в силу непрерывности на границе интервала также обращается в нуль:

. (21.24)

Осталось записать и решить уравнение Шрёдингера на интервале , где :

Вводим обозначение для волнового числа:

, (21.25)

. (21.26)

Решение этого уравнения имеет смысл записать в виде синуса; тогда автоматически удовлетворим требованию непрерывности волновой функции на левом конце интервала ( ):

. (21.27)

Должно также выполняться условие:

;

. (21.28)

Здесь n – квантовое число; оно может принимать значения

Для энергии из (21.25):

. (21.29)

Получено квантование энергии: энергия частицы может принимать только дискретные значения (рис.21.12), которые даёт соотношение (21.28). Минимальное значение энергия принимает при :

Минимальное значение энергии не может быть равным нулю в силу принципа неопределённостей.

Из (21.27) и (21.28) получим соответствующие этим уровням энергии волновые функции:

. (21.30)

При ;

при ;

и т.д. (см. графики функций рис.21.13).

А
мплитуду А волновой функции находим из условия нормировки (21.15):

;

. (21.31)

Расстояние между соседними уровнями энергии из (21.29):

. (21.31)

Относительное расстояние между уровнями уменьшается при увеличении квантового числа n:

Для больших квантовых чисел n дискретность уровней энергии уже не играет роли; относительное расстояние между ними уменьшается. Это – проявление принципа соответствия: при больших квантовых числах (большая энергия) законы квантовой механики дают тот же результат, что и классическая механика; энергию можно считать изменяющейся непрерывно.

Рассчитаем расстояние между уровнями энергии при n=1 по (21.31) для электрона в потенциальной яме шириной:

порядка размера атома :

для макротела размером :

В первом случае дискретность уровней энергии существенна; во втором случае уровни так близки, что энергию можно считать изменяющейся непрерывно.

8.3. Линейный гармонический осциллятор

Классический гармонический осциллятор – например, грузик массой m на пружинке жёсткостью – колеблется под действием силы упругости в потенциальном поле вида (рис.21.14):

. (21.32)

Полная энергия сохраняется, только перераспределяется между потенциальной и кинетической:

. (21.33)

Максимальное смещение грузика определяется запасом полной энергии системы. Координата x изменяется в пределах:

При небольших деформациях пружины, когда ещё выполняется закон Гука, и справедлива зависимость (21.32), колебания гармонические и происходят по закону:

с циклической частотой, определяемой параметрами системы – массой груза и жёсткостью пружины:

; .

Поскольку в поворотных точках при скорость v обращается в нуль; вблизи этих точек грузик движется медленно; так что вероятность обнаружения грузика при максимальна.

б) Квантовый гармонический осциллятор

Потенциальную энергию квантового осциллятора возьмём в том же виде, как и для классического осциллятора.

; .

Здесь величина может быть, например, жёсткостью упругих связей ядер в молекуле; m – масса ядра. Запишем одномерное стационарное уравнение Шрёдингера с такой потенциальной функцией:

. (21.34)

Решать это уравнение мы не будем; приведём результаты.

Уравнение (21.34) имеет решение не при любых значениях полной энергии E, а только при:

, (21.35)

где υ – колебательное квантовое число, принимающее целочисленные значения

Полная энергия не может обращать в ноль; её минимальное значение в основном состоянии системы при

Это – так называемые нулевые колебания, следствие принципа неопределённостей. Волновая функция основного состояния выглядит так:

Все уровни энергии отстоят друг от друга на одинаковом расстоянии (рис.21.15), равном

Переходы этой колебательной системы возможны только между соседними уровнями; при этом излучается или поглощается энергия, равная . На рис.21.15 приводятся также графики – квадрата модуля волновой функции (плотности вероятности) для соответствующих состояний. Видно, что:

Вероятность найти частицу за пределами потенциальной ямы в области, запрещённой классической механикой, отлична от нуля, хотя и быстро убывает.
Для больших квантовых чисел вблизи поворотных точек амплитуда волновой функции максимальна, то есть вероятность найти в них частицу максимальна, как и в классическом рассмотрении. Это работает принцип соответствия.

8.4. Ангармонический осциллятор

В общем случае любая функция, в том числе и потенциальная энергия как функция координаты x, раскладывается в ряд: