Рассматривать будем на таком примере:
Если говорить о действительных числах, то, вы знаете, что корень из отрицательного числа нельзя извлекать. Однако в комплексных числах можно. Если конкретнее, 2 корня:
Выполним проверку того, что эти корни и права оказываются решением уравнения:
Что и требовалось доказать.
Зачастую используют сокращенную запись, корни записывают в одну строчку в таком виде: 
Такие корни являются сопряженными комплексными корнями.
Теперь вы знаете как можно извлечь квадратный корень из отрицательного числа. Приведем еще несколько примеров:




В каждом случае получаем 2 сопряженных комплексных корня.
Решим квадратное уравнение 
Первым шагом определим дискриминант уравнения:
В нашем случае дискриминант оказался отрицательным, и в случае с действительными числами у уравнения нет решений, но у нас вариант с комплексными числами, поэтому можем продолжать решение:
Как известно из формул дискриминанта у нас образуется 2 корня:

Т.о., у уравнения 

Теперь можно решить любое квадратное уравнение!
У любого уравнения с многочленом n-ой степени 
- Как извлечь корень из произвольного комплексного числа?
- Решить квадратное уравнение, корни уравнения во всех известных формах и изобразить геометрически: z2+1-2iz-2i=0
- Условие
- Решение
- Зарегистрируйся, чтобы продолжить изучение работы
- Корни уравнения записать во всех известных формах и изобразить геометрически
- Правила ввода выражений и функций
- Где учитесь?
- 📸 Видео
Видео:КОМПЛЕКСНЫЕ ЧИСЛА ДЛЯ ЧАЙНИКОВ ЗА 7 МИНУТСкачать

Как извлечь корень из произвольного комплексного числа?
Рассмотрим уравнение z n = w, либо, записав в другом виде: 
В частности, при n = 2 получаем квадратный корень 
У уравнения типа 

где 
φ – его аргумент,
а параметр k принимает значения: 
Найдем корни уравнения: 
Перепишем уравнение как: 
В этом примере 



Далее найдем модуль и аргумент комплексного числа 
Число w находится в 1-ой четверти, значит:
Помним, что определяя тригонометрическую форму комплексного числа лучше делать чертеж.
Детализируем еще немного общую формулу:


Так подобно расписывать не обязательно. Здесь мы это сделали, что бы было ясно откуда что образовалось.
Подставляем в формулу значение k = 0 и получаем 1-й корень:

Подставляем в формулу значение k = 1 и получаем 2-й корень:

Ответ: 
Если необходимо, корни, которые мы получили можно перевести обратно в алгебраическую форму.
Часто вычисленные корни нужно изобразить геометрически:
Как выполнить чертеж?
Для начала на калькуляторе вычисляем, чему равен модуль корней 
Далее берем аргумент 1-го корня 

Отмеряем транспортиром 45° и ставим на чертеже точку z0.
Берем аргумент 2-го корня 

По этому же алгоритму ставим точку z2.
Видно, что корни располагаются геометрически правильно с интервалом 
Видео:Математика без Ху!ни. Комплексные числа, часть 3. Формы записи. Возведение в степень.Скачать

Решить квадратное уравнение, корни уравнения во всех известных формах и изобразить геометрически: z2+1-2iz-2i=0
- Реферат.Справочник
- Контрольные работы по высшей математике
- Решить квадратное уравнение, корни уравнения во всех известных формах и изобразить геометрически: z2+1-2iz-2i=0
Условие
Решить квадратное уравнение, корни уравнения во всех известных формах и изобразить геометрически: z2+1-2iz-2i=0
Решение
Дискриминант к квадратичной зависимости иметь вид
D=1-2i2-4∙-2i)=-3+4i
Дискриминант комплексный. Для нахождения значения корня с дискриминанта используем формулу Муавра
nz=nzcosφ+2πkn+isinφ+2πkn, k=0,1,…(n-1)
Запишем полученный дискриминант в тригонометрической форме
Представим комплексное число4-3i в тригонометрической форме .
Здесь x=-3 0, r=-32+42=5,
φ=arctgyx==π-arctg43 , Поэтому
-3+4i=5cosπ-arctg43+isinπ-arctg43
Отсюда записываем значение модуля и аргумента D
r=5,φ=π-arctg43
и подставляем у формулы корней
D=5cosπ-arctg43+2πk2+isinπ-arctg43+2πk2, где k=0,1
Полагая k=0,1 получим:
D1=5cosπ-arctg432+isinπ-arctg432=50,448+0,525i=
≈1+2i
D2=5cos3π-arctg432+isin3π-arctg432=5-0,449-0,893i=
=-1-2i
Решения квадратного уравнения вычислим по формулам
x1=-1-2i+1+2i2=2i=2cosπ2+sinπ2=eπ2i
x2=-1-2i-1-2i2=-1=cosπ+sinπ=eiπ
Зарегистрируйся, чтобы продолжить изучение работы
.
Здесь x=-3 0, r=-32+42=5,
φ=arctgyx==π-arctg43 , Поэтому
-3+4i=5cosπ-arctg43+isinπ-arctg43
Отсюда записываем значение модуля и аргумента D
r=5,φ=π-arctg43
и подставляем у формулы корней
D=5cosπ-arctg43+2πk2+isinπ-arctg43+2πk2, где k=0,1
Полагая k=0,1 получим:
D1=5cosπ-arctg432+isinπ-arctg432=50,448+0,525i=
≈1+2i
D2=5cos3π-arctg432+isin3π-arctg432=5-0,449-0,893i=
=-1-2i
Решения квадратного уравнения вычислим по формулам
x1=-1-2i+1+2i2=2i=2cosπ2+sinπ2=eπ2i
x2=-1-2i-1-2i2=-1=cosπ+sinπ=eiπ
Оплатите контрольную работу или закажите уникальную работу на похожую тему
Видео:Комплексные корни квадратных уравнений. 11 класс.Скачать

Корни уравнения записать во всех известных формах и изобразить геометрически
Квадратный корень из комплексного числа
Деление комплексных чисел
Умножение комплексных чисел
Корни четвертой и пятой степени
Реальная часть комплексного числа
Возведение в степень
Мнимая и действительная часть
Модуль комплексного числа
Комплексный знак числа
Можно использовать следующие функции от z (например, от z = 1 + 2.5j):
Правила ввода выражений и функций
3.14159.. e Число e — основание натурального логарифма, примерно равно
2,7183.. i Комплексная единица oo Символ бесконечности — знак для бесконечности
© Контрольная работа РУ — калькуляторы онлайн
Видео:Изобразить область на комплексной плоскостиСкачать

Где учитесь?
Для правильного составления решения, укажите:
📸 Видео
Математика без Ху!ни. Комплексные числа, часть 4. Извлечение корня n-й степени.Скачать

Комплексные корни квадратного уравненияСкачать

Изображение комплексных чисел. Модуль комплексного числа. 11 класс.Скачать

Тригонометрическая форма комплексного числаСкачать

Биквадратное уравнение. Комплексные корни.Скачать

Встреча с Путиным в общежитии МГУ на Воробьевых горах!Скачать

Найдите все значения корня из комплексного числа ∛-125i ★ Извлечение корня из комплексного числаСкачать
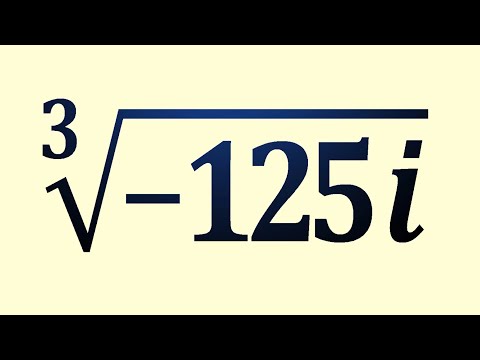
10 класс, 34 урок, Тригонометрическая форма записи комплексного числаСкачать

Мнимые числа реальны: #1-13 [Welch Labs]Скачать
![Мнимые числа реальны: #1-13 [Welch Labs]](https://i.ytimg.com/vi/kicp_odjsRs/0.jpg)
Формула Муавра ➜ Вычислить ➜ (5+5i)⁷Скачать

2. Геометрическая интерпретация комплексных чисел. Модуль и аргумент комплексного числаСкачать

Комплексные числа: коротко и понятно – Алексей Савватеев | Лекции по математике | НаучпопСкачать

Математика без Ху!ни. Комплексные числа, часть 1. Введение.Скачать

4. Показательная форма комплексного числаСкачать

3,5 способа отбора корней в тригонометрии | ЕГЭ по математике | Эйджей из ВебиумаСкачать

Комплексные числа: алгебраическая форма и действия над ними | Высшая математикаСкачать


















