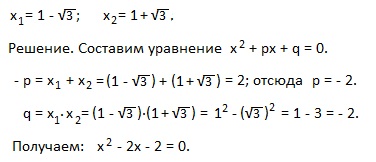Корни приведенного квадратного уравнения x2 px q

Видео:Алгебра 8 класс (Урок№19 - Уравнение х² = а.)Скачать

8.2.3. Теорема Виета

I. Теорема Виета для приведенного квадратного уравнения.

Сумма корней приведенного квадратного уравнения x 2 +px+q=0 равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену:

Найти корни приведенного квадратного уравнения, используя теорему Виета.

Пример 1) x 2 -x-30=0. Это приведенное квадратное уравнение ( x 2 +px+q=0), второй коэффициент p=-1, а свободный член q=-30. Сначала убедимся, что данное уравнение имеет корни, и что корни (если они есть) будут выражаться целыми числами. Для этого достаточно, чтобы дискриминант был полным квадратом целого числа.

Находим дискриминант D=b 2 — 4ac=(-1) 2 -4∙1∙(-30)=1+120=121=11 2 .

Теперь по теореме Виета сумма корней должна быть равна второму коэффициенту, взятому с противоположным знаком, т.е. (-p), а произведение равно свободному члену, т.е. (q). Тогда:

x₁+x₂=1; x₁∙x₂=-30. Нам надо подобрать такие два числа, чтобы их произведение было равно -30, а сумма – единице. Это числа -5 и 6. Ответ: -5; 6.

Пример 2) x 2 +6x+8=0. Имеем приведенное квадратное уравнение со вторым коэффициентом р=6 и свободным членом q=8. Убедимся, что есть целочисленные корни. Найдем дискриминант D₁, так как второй коэффициент – четное число. D₁=3 2 -1∙8=9-8=1=1 2 . Дискриминант D₁ является полным квадратом числа 1, значит, корни данного уравнения являются целыми числами. Подберем корни по теореме Виета: сумма корней равна –р=-6, а произведение корней равно q=8. Это числа -4 и -2.

На самом деле: -4-2=-6=-р; -4∙(-2)=8=q. Ответ: -4; -2.

Пример 3) x 2 +2x-4=0. В этом приведенном квадратном уравнении второй коэффициент р=2, а свободный член q=-4. Найдем дискриминант D₁, так как второй коэффициент – четное число. D₁=1 2 -1∙(-4)=1+4=5. Дискриминант не является полным квадратом числа, поэтому, делаем вывод: корни данного уравнения не являются целыми числами и найти их по теореме Виета нельзя. Значит, решим данное уравнение, как обычно, по формулам (в данном случае по формулам для частного случая с четным вторым коэффициентом). Получаем:

Пример 4). Составьте квадратное уравнение по его корням, если x₁=-7, x₂=4.

Решение. Искомое уравнение запишется в виде: x 2 +px+q=0, причем, на основании теоремы Виета –p=x₁+x₂=-7+4=-3 → p=3; q=x₁∙x₂=-7∙4=-28. Тогда уравнение примет вид: x 2 +3x-28=0.

Пример 5). Составьте квадратное уравнение по его корням, если:

II. Теорема Виета для полного квадратного уравнения ax 2 +bx+c=0.

Сумма корней равна минус b, деленному на а, произведение корней равно с, деленному на а:

Пример 6). Найти сумму корней квадратного уравнения 2x 2 -7x-11=0.

Решение.

Убеждаемся, что данное уравнение будет иметь корни. Для этого достаточно составить выражение для дискриминанта, и, не вычисляя его, просто убедиться, что дискриминант больше нуля. D=7 2 -4∙2∙(-11)>0. А теперь воспользуемся теоремой Виета для полных квадратных уравнений.

Пример 7). Найдите произведение корней квадратного уравнения 3x 2 +8x-21=0.

Решение.

Найдем дискриминант D₁, так как второй коэффициент (8) является четным числом. D₁=4 2 -3∙(-21)=16+63=79>0. Квадратное уравнение имеет 2 корня, по теореме Виета произведение корней x₁∙x₂=c:a=-21:3=-7.

Видео:Уравнение x^2+px+q=0 имеет корни -6; 4. Найдите q. | ОГЭ 2017 | ЗАДАНИЕ 4 | ШКОЛА ПИФАГОРАСкачать

Квадратные уравнения

Квадратное уравнение или уравнение второй степени с одним неизвестным — это уравнение, которое после преобразований может быть приведено к следующему виду:

ax 2 + bx + c = 0 — квадратное уравнение,

где x — это неизвестное, а a, b и c — коэффициенты уравнения. В квадратных уравнениях a называется первым коэффициентом (a ≠ 0), b называется вторым коэффициентом, а c называется известным или свободным членом.

называется полным квадратным уравнением. Если один из коэффициентов b или c равен нулю, или нулю равны оба эти коэффициента, то уравнение представляют в виде неполного квадратного уравнения.

Видео:Квадратные уравнения от «А» до «Я». Классификация, решение и теорема Виета | МатематикаСкачать

Приведённое квадратное уравнение

Полное квадратное уравнение можно привести к более удобному виду, разделив все его члены на a, то есть на первый коэффициент:

Затем можно избавиться от дробных коэффициентов, обозначив их буквами p и q:

то получится x 2 + px + q = 0.

Уравнение x 2 + px + q = 0 называется приведённым квадратным уравнением. Следовательно, любое квадратное уравнение, в котором первый коэффициент равен 1, можно назвать приведённым.

является приведённым, а уравнение:

можно заменить приведённым уравнением, разделив все его члены на -3:

Видео:Теорема Виета. Алгебра, 8 классСкачать

Решение квадратных уравнений

Чтобы решить квадратное уравнение, надо привести его к одному из следующих видов:

Для каждого вида уравнения есть своя формула нахождения корней:

Вид уравнения	Формула корней
ax 2 + bx + c = 0
ax 2 + 2kx + c = 0
x 2 + px + q = 0	или если коэффициент p нечётный

Обратите внимание на уравнение:

это преобразованное уравнение ax 2 + bx + c = 0, в котором коэффициент b — четный, что позволяет его заменить на вид 2k. Поэтому формулу нахождения корней для этого уравнения можно упростить, подставив в неё 2k вместо b:

Пример 1. Решить уравнение:

Так как в уравнении второй коэффициент не является чётным числом, а первый коэффициент не равен единице, то искать корни будем по самой первой формуле, называемой общей формулой нахождения корней квадратного уравнения. Сначала определим, чему равны коэффициенты:

Теперь, для нахождения корней уравнения, просто подставим значения коэффициентов в формулу:

Определим, чему равны коэффициенты:

Так как в уравнении второй коэффициент — чётное число, то будем использовать формулу для квадратных уравнений с чётным вторым коэффициентом:

Приведём уравнение к общему виду:

Определим, чему равны коэффициенты:

Так как первый коэффициент равен 1, то будем искать корни по формуле для приведённых уравнений с чётным вторым коэффициентом:

Определим, чему равны коэффициенты:

Так как первый коэффициент равен 1, то будем искать корни по формуле для приведённых уравнений с нечётным вторым коэффициентом:

Видео:Формула корней квадратного уравнения. Алгебра, 8 классСкачать

Корни приведённого квадратного уравнения X2 + px + q = 0 можно найти по формуле?

Алгебра | 5 — 9 классы

Корни приведённого квадратного уравнения X2 + px + q = 0 можно найти по формуле.

Решите уравнение воспользовавшись этой формулой.

X2 — 8x + 12 = 0 x = X1 = X2 =.

D = b² — 4ac = 8² — 4 * 1 * 12 = 64 — 48 = 16 = 4²

х = ( — b±√D) / 2a = (8±4) / 2

х₁ = (8 + 4) / 2 = 12 / 2 = 6

х₂ = (8 — 4) / 2 = 4 / 2 = 2

будут вопросы, пиши

отметь, как лучшее, пожавлуйста.

Видео:Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

Не используя формулу корней, решите квадратное уравнение x2 — 8x — 9 = 0?

Не используя формулу корней, решите квадратное уравнение x2 — 8x — 9 = 0.

Видео:ТЕОРЕМА ВИЕТА ЗА 2 МИНУТЫСкачать

Формула корней квадратных уравнений : 2х ^ — 5х + 1 = 0?

Формула корней квадратных уравнений : 2х ^ — 5х + 1 = 0.

Видео:Свойства квадратного корня. Уравнение х2=а, 8 классСкачать

Формула корней квадратного уравнения 3х2 — 2х — 1 = 0?

Формула корней квадратного уравнения 3х2 — 2х — 1 = 0.

Видео:Теорема Виета для приведенных квадратных уравненийСкачать

Помогите, решите уравнения 3z ^ 2 = 198 + 15zТема : Формула корней квадратного уравнения ?

Помогите, решите уравнения 3z ^ 2 = 198 + 15z

Тема : Формула корней квадратного уравнения .

Видео:5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

Не используя формулу корней, найдите корни квадратного уравнения : Как найти не используя формулы корней ?

Не используя формулу корней, найдите корни квадратного уравнения : Как найти не используя формулы корней ?

X ^ + 8x + 7 = 0 x ^ — 19x + 18 = 0.

Видео:Теорема Виета. 8 класс.Скачать

Решите квадратное уравнение по общей формуле?

Решите квадратное уравнение по общей формуле.

Видео:Неполные квадратные уравнения. Алгебра, 8 классСкачать

Помогите пожалуйста?

Я не могу решить 135 номер.

Меня на этой тебе не было в школе.

Знаю только формулу — дискриминант.

И тему проходим в данный момент — «Приведённое квадратное уравнение.

Формулы корней квадратного уравнения.

Видео:Быстрый способ решения квадратного уравненияСкачать

По какой формуле можно найти корни квадратного уравнения решаемого при помощи дискрименанта?

По какой формуле можно найти корни квадратного уравнения решаемого при помощи дискрименанта?

Видео:Алгебра 10 класс (Урок №1 - Многочлен P(x) и его корень. Алгебраическое уравнение.)Скачать

Запишите формулу корней квадратного уравнения с четным вторым коэффициентом?

Запишите формулу корней квадратного уравнения с четным вторым коэффициентом.

Видео:Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnlineСкачать

Выведите формулу для суммы и произведений корней квадратного уравнения?

Выведите формулу для суммы и произведений корней квадратного уравнения.

На этой странице вы найдете ответ на вопрос Корни приведённого квадратного уравнения X2 + px + q = 0 можно найти по формуле?. Вопрос соответствует категории Алгебра и уровню подготовки учащихся 5 — 9 классов классов. Если ответ полностью не удовлетворяет критериям поиска, ниже можно ознакомиться с вариантами ответов других посетителей страницы или обсудить с ними интересующую тему. Здесь также можно воспользоваться «умным поиском», который покажет аналогичные вопросы в этой категории. Если ни один из предложенных ответов не подходит, попробуйте самостоятельно сформулировать вопрос иначе, нажав кнопку вверху страницы.

Y'(х) = / (3) / 2 + sinx y'(х) = 0 / (3) / 2 + sinx = 0 sinx = — / (3) / 2 x = — п / 3 + 2пn, n — целое число х = — 2п / 3 + 2пk, k — целое число — п.

4 не поняла задание, но вроде так. 2 во вложениях.

AB = 180˚, MD — биссектриса CMB. AB — CMA = 180˚ — 52˚ = 128˚, так как MD биссекириса , то DMB = 128˚ : 2 = 64˚ Ответ : 64°.

3 ^ (1 / 48) * 3 ^ (1 / 16) : 3 ^ (1 / 12) = 3 ^ (1 / 48 + 1 / 16 — 1 / 12) = 3° = 1.

📹 Видео

УРАВНЕНИЕ х²=а корни уравненияСкачать

Алгебра 8. Урок 9 - Квадратные уравнения. Полные и неполныеСкачать

Составьте квадратное уравнение, корнями которого являются числаСкачать

8 класс. Квадратные уравнения. x2=aСкачать

Теорема Виета для квадратного уравнения.Скачать